多模态耦合特征子空间正则的SVDD
王 闯,胡文军,刘 闯,王余波
(1.湖州师范学院 信息工程学院,浙江 湖州 313000; 2.浙江省现代农业资源智慧管理与应用研究重点实验室,浙江 湖州 313000)
0 引 言
在诸多的应用领域,如机器故障[1]、医疗诊断[2]、网络安全[3]等,正常数据的获取较容易,而异常数据的获取则非常困难或代价昂贵,这使得在对该类问题建模时只有一类数据可供使用.支持向量数据描述(Support Vector Data Description,SVDD)[4]作为典型的一类分类方法,得到了研究者的广泛关注,其目的是要在特征空间中找到一个能够包含绝大多数正常样本且半径尽可能小的超球.一些改进算法也随之提出.Wu等为增大超球的决策边界与少量异常样本之间的间隔,提出一种小球体大间隔的支持向量数据描述方法[5];胡文军等为提高SVDD的决策速度,提出一种SVDD的快速实时决策方法[6],其将SVDD决策时间的复杂度降至O(1);Wang等为每个样本设计基于位置的权重,提出位置正则的支持向量数据描述[7];Cha等为每个样本设计基于密度的权重,提出基于密度加权的支持向量数据描述[8];为避免少量异常样本数据对SVDD建模的影响,胡天杰等从高斯核空间正常样本的全局分布出发,提出分布熵惩罚的支持向量数据描述[9];Hu等则从高斯核空间综合样本的全局分布结构与局部分布结构,提出全局加局部联合正则的支持向量数据方法[10].上述方法虽然在一类分类问题中取得了较好效果,但这些方法均要求训练的数据来自同一模态,即单模态数据.
模态是指研究对象的信息来源方式.若对象的信息来源于一种方式,则对应的数据称为单模态数据,反之称为多模态数据.在现实中,多模态数据的应用场景十分广泛.例如,结合视觉和听觉的电影观赏;综合视觉、嗅觉、听觉的化工环境监测;综合视频信息、传感信息的机器故障诊断等[11].由于多模态数据的来源并不唯一,其各模态的维度也不尽相同,故直观的方法是先将所有的模态数据投影到同一低维子空间,再利用传统的机器学习方法进行建模.例如:Li等从多模态数据抗噪角度出发,提出一种稀疏子空间聚类方法[12];Wang等针对多模态数据存在的冗余问题,将子空间学习与特征选择相结合,应用于跨模态检索[13];针对多模态数据的一类分类问题,Sohrab等将多模态数据映射到低维子空间,在子空间考虑数据协方差,并实施SVDD建模.该方法称为多模态子空间支持向量数据描述(Multimodal Subspace SVDD,MS-SVDD)[14].
MS-SVDD拓展传统方法,以解决多模态分类问题,但其基于“一致性”假设为前提,即在低维子空间下的各模态是一致的.实际上,多模态数据之间既存在“一致性”,又存在“互补性”[15],这意味着各模态数据的特征间相互耦合,在多模态学习中势必存在特征冗余和特征间相互干扰的问题.此外,MS-SVDD并没有充分考虑模态内与模态间的数据结构关系[16-17],使得隐藏在其中的潜在信息无法被充分利用.针对这两个问题,本文分别设计稀疏投影矩阵正则项和多模态图正则项,前者用来减小特征之间的相互耦合,后者用来保持模态内和模态间的结构关系.本文将上述两个正则项施加到SVDD上,提出耦合特征子空间正则的支持向量数据描述(Coupled Feature Subspace Regularized SVDD,CFSR-SVDD)方法.
1 相关工作
给定单模态数据集X=(x1,…,xN),其中xi∈d是第i个样本,N和d分别是样本数和特征维度.给定M个模态数据集其中Dm是第m个模态的第i个样本,Nm和Dm分别是第m个模态的样本数和特征维度,是投影到D维子空间后的表示,即其中Qm∈D×Dm是第m个模态的投影矩阵.
1.1 SVDD
SVDD针对单模态数据建模,其目的是寻找一个包含大部分正常样本的超球.该问题可描述为:
(1)
其中,R、a分别为超球的半径与球心,ξi为引入的松弛变量,C为惩罚参数.利用拉格朗日技巧可得到上述问题的对偶形式:
(2)
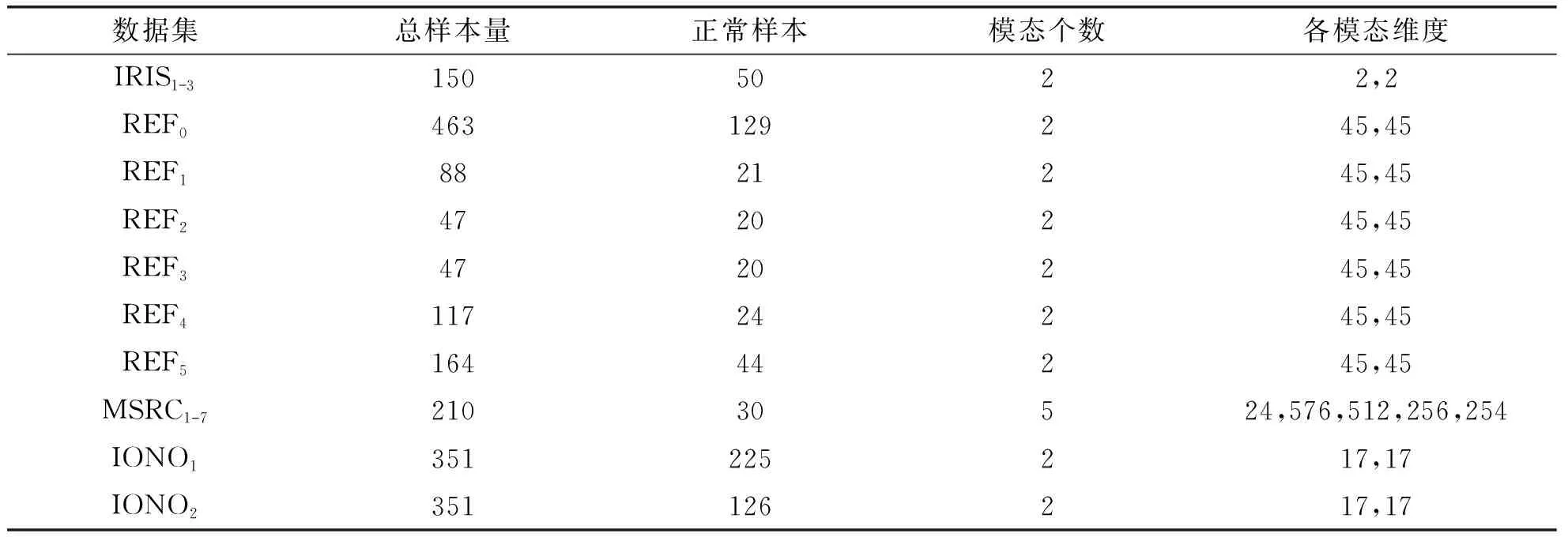
其中,α=(α1,…,αN)T≥0为拉格朗日乘子向量,〈•,•〉为向量内积.显然,式(2)是标准的二次规划问题(Quadratic Programming,QP).根据KKT(Karush-Kuhn-Tucker)[18]条件可知,当0<αi (3) 对任意未知样本z∈d,可通过式(4)决策: (4) 当f(z)≤R2时,样本z为正常样本,反之为异常样本. 为推广SVDD应用到多模态数据,Sohrab等[14]先将所有模态的数据投影到同一个低维子空间,然后实施传统的SVDD建模.该方法称为MS-SVDD,其数学模型为: (5) (6) 第一步:固定Qm,求解αm.式(6)退化为式(7): (7) (8) 求解式(8)的标准QP问题,可得最优解αm,并根据KKT条件可计算子空间超球半径R. (9) 为保持多模态数据之间的一致性,构建一个更合适的SVDD分类边界.Sohrab等在模型优化时引入多模态数据集的协方差ω,即式(9)转化为式(10): (10) 其中,λ为控制ω重要性的权重参数.通过组合子空间的数据,Sohrab等设计了7种协方差表示方法[14,19].式(10)采用梯度下降的方式迭代求解. 对含有m个模态的任意未知样本z,在决策时,首先通过各自模态的投影矩阵Qm,将各模态投影到同一D维子空间,然后利用式(4)对子空间的各模态进行分类,最后依据决策策略对样本z做最终决策.关于决策策略的内容可参考文献[14]. MS-SVDD不但忽略了数据间原始结构关系,而且忽略了多模态数据特征间相互耦合问题,从而导致数据间的潜在信息无法被充分挖掘.针对这些问题,本文将多模态图的正则项引入传统的SVDD中,以尽可能地挖掘蕴含在数据结构间的潜在信息[20],并将稀疏投影矩阵的正则项引入传统的SVDD中,以减小特征耦合的影响.实际上,对投影矩阵施加L2,1范数是解决特征间耦合的一种常用做法[21].式(11)给出了CFSR-SVDD方法的理论模型: (11) 多模态数据包含模态内和模态间两种结构关系.单个模态内的数据在映射到低维子空间时,应该保持原始样本空间数据的邻域关系,这就是模态内的结构关系.模态间的结构关系是指当不同模态的数据表示相同的内容或主题时,它们应该具有上层语义的相似关系.为保持多模态数据这两种结构关系,本文提出多模态图正则项,其由近邻相似图和语义相似图构成. 2.1.1 近邻相似图 (12) 为保持所有模态内的结构关系,最小化式(13): (13) 2.1.2 语义相似图 (14) 为保持所有模态间的结构关系,则最小化式(15): (15) 为方便,本文利用近邻相似图矩阵Gmm和语义相似图矩阵Gmp构建一个相似度矩阵G: (16) (17) (18) 其中,Sm为对角矩阵.对角元素可由式(19)计算: (19) 将多模态图正则项的优化式(17)与稀疏投影矩阵正则项的优化式(18)代入目标函数式(11),得到CFSR-SVDD方法的优化模型: (20) 利用拉格朗日技巧构造以下拉格朗日函数: (21) 为求解式(21),本文采用两步交替迭代的方法. 第一步:固定Qm,求解αm和Sm.由于Sm仅与Qm相关,当Qm固定时,Sm可通过式(20)计算.此时式(21)退化为式(22),即: (22) (23) (24) (25) (26) (27) (28) 对式(28)求L7关于Qm的偏导,可得: (29) 式(29)采用式(30)的梯度下降方式迭代求解: (30) 其中,η为学习率. 对未知样本x,首先根据维度确定其可能隶属的模态,然后利用对应模态的投影矩阵将该样本映射到D维子空间.在获得其对应的子空间后,用y表示,通过式(31)对其进行分类: (31) 当f(y)≤R2时,y为正常表示,反之为异常表示.由于一个未知样本可能隶属于多个模态,即可能得到多个子空间表示.为决策未知样本x的最终类别,本文设计两种决策策略:①和策略.当且仅当该样本点的所有表示都被分类为正常表示时,该样本点被分类为正常样本,反之为异常样本;②或策略.当该样本点有任意一个表示被分类为正常表示时,该样本被分类为正常样本,反之为异常样本. CFSR-SVDD方法的时间复杂度主要由三部分组成:QP问题的求解、投影矩阵的更新、投影矩阵的正交化和单位化. 表1 时间复杂度对比 为验证CFSR-SVDD方法的有效性,本文在MSRC-v1图像数据集和多个UCI数据集上进行实验.数据集的简介见表2,详细信息可参见文献[34]和https://archive.ics.uci.edu/ml/index.php.各数据集多模态的划分见以下所述. 表2 数据集简介 IRIS[30]数据集包含3个类,每类的样本量均为50,每个样本含有4个特征.本文将萼片的长度和宽度特征视为第一个模态,将花瓣的长度和宽度特征视为第二个模态.本文分别选取其中的一个类作为目标类,将另外两个类视为异常类,从而得到3个子数据集IRIS1-3.Robot Execution Failures (REF)[31]数据集包含不同触发事件的5个子数据集REF1-5,将所有子数据集整合在一起,得到子数据集REF0,对每个数据集,本文将力和力矩特征视为不同的2个模态,并将机器正常运行下获得的样本视为正常样本,其余视为异常样本.MSRC-v1[32]图像数据集包含240张图片.根据文献[33],本文分别挑选其中的7个类作为训练集,从而得到7个子数据集MSRC1-7.本文将5种不同的视觉特征提取视为同一对象所对应的5种不同模态.在实验中,将每个类分别选择为目标类,其余类视为异常类.IONOSPHERE[34]数据集包含2个类,分别包含225个样本和126个样本.本文将脉冲的2个状态作为两种不同的模态,并将每个类分别选择为目标类,其余类为异常类,从而得到2个子数据集IONO1-2. 实验环境:Intel(R) Core(TM) i5-9400 CPU @ 2.90GHz8 GB RAM,64位Windows 10,MatlabR2020a. 参数设置:为统一实验过程,消除奇异样本对实验的影响,本文首先将所有特征归一化到[-1,1],再采用十折交叉验证进行实验,即每次选取正常样本中不同的九部分作为训练样本,剩余一部分和所有的异常样本作为测试样本.惩罚参数C从{0.01k,0.1k},k=1,…,10中寻优;权重参数μ1、μ2均默认取1;平衡参数β从{10-3,10-2,10-1,10°,101,102}中寻优;近邻相似图矩阵核宽δ从{0.01,0.1,1,10}中寻优;子空间的维度D从{2,5,10,15,20}中寻优,其中D满足D≤min{D1,…,DM,N1,…,NM};学习率η∈{0.01,0.1};最大迭代次数τ设置为20.为保证实验的有效性和可对比性,有关对比方法的参数选择与上述范围一致. (32) (33) 本文选取SVDD、OCSVM和MS-SVDD作为对比方法,由于MS-SVDD的7种协方差表述方法大同小异,因此在多次实验后,选取具有代表性的第二、第四和第六种协方差表述方法进行展示,分别表示为MS-SVDDI-III.此外,所有方法在同一低维子空间中选取最优的决策策略结果进行对比分析.表3展示了CFSR-SVDD在多个数据集上进行十折交叉验证后GM的平均值和方差. 表3 GM实验结果 CFSR-SVDD与对比方法的几何精度对比见表3.由表3可见,本文所提出的CFSR-SVDD对上述多模态数据集的分类精度大多达83%以上.其中,在MSRC1和MSRC7数据集上,SVDD的分类精度最高,达到86.3%和87.2%;在REF4数据集上,MS-SVDDII的分类精度最高,达到95.4%;在其余数据集上,CFSR-SVDD都取得最好的效果,甚至在IRIS1上达到极致. 综上所述,本文所提出的CFSR-SVDD,在一定程度上提高了多模态数据应用一类分类问题的准确率,这是因为CFSR-SVDD在数据投影到子空间时,不仅引入多模态图正则项,以保持模态内和模态间的结构关系,而且引入稀疏投影矩阵正则项,以降低特征间的相互干扰.表3的实验结果也佐证了CFSR-SVDD的有效性. 本文提出一种新的多模态一类分类方法,该方法将所有模态的数据投影到同一个低维子空间,在投影过程中不仅利用多模态图正则项,以保持模态内和模态间的结构信息,而且结合稀疏投影矩阵正则项,从多模态数据中选择有区别的特征,以减小特征之间的耦合,降低特征冗余的影响,使整体模型用于优化多模态一类分类任务的数据描述.实验结果显示,CFSR-SVDD在绝大部分数据集上要优于对比方法,且更加稳定.但CFSR-SVDD方法也存在不足,如建模过程不包含异常样本、决策过程较为简单等问题.在今后的工作中,我们将尝试解决这些问题,并考虑其他不同方向的改进.1.2 多模态子空间SVDD



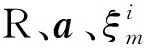
2 耦合特征子空间正则的SVDD
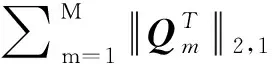
2.1 多模态图正则项
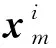
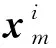



2.2 稀疏投影矩阵正则项

2.3 模型优化


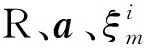

2.4 模型决策
3 时间复杂度

4 实 验
4.1 数据集与预处理
4.2 实验设置
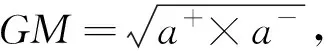
4.3 实验结果与分析

5 结 论

