浅谈大学物理教学中微分和积分思想的应用

赵朝军 张 昱

西安工商学院 陕西西安 710200

1 概述

大学物理是理工科专业学生的一门基础课,学生通过课程的学习,可以充分借助高等数学工具解决物理学中的大量实际问题,从而具备定量计算的能力,进一步促进学生工程技术素养的提升。

在高等数学中,微分的中心思想是无限分割。设函数y=f(x)在x0的某一领域内有定义,当x在x0处取增量Δx时,如果Δy能够写成Δy=f(x0+Δx)-f(x0)=A·Δx+o(Δx)(A与Δx无关),那么称y=f(x)在点x0可微,A·Δx称为y=f(x)在点x0的微分,可以记作dy|x=x0或者df(x0),即dy|x=x0=A·Δx,微分是函数改变量的线性主要部分,此处给定一元型的微分。当然,在实际的问题中,还会涉及多元型和高阶型的微分。早在希腊时期,人类就开始研究极限、无穷分割等概念,当时由于客观条件的制约,研究的某些结论并不完全正确,却体现了人类研究微分的第一步。17世纪时期,费马提及计算函数的极大值和极小值的步骤,这实际上已被现代微分学所用,即设函数导数为零,进而求出函数极点的方法。另外,巴罗透过微分三角形求出切线的方程,这和现代微分学中用导数求切线的方法是一样的,可见人类在17世纪已经掌握了微分的要领。

17世纪的中期,微分和积分仍然被看作两个独立的概念,但是,牛顿和莱布尼茨经过大量深入的研究,通过牛顿—莱布尼茨公式将微分和积分巧妙地连接起来,说明了积分是微分的逆运算,微分也是积分的逆运算,这是微积分发展历史上非常重要的时刻,也是微积分理论中的重要基石。

2 大学物理中的微分和积分思想应用实例

2.1 计算刚体的转动惯量

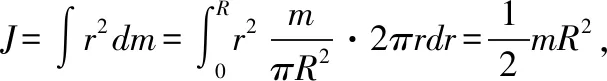
2.2 计算带电体的电量

如图2,有一带电量为+q,半径为R均匀带电细圆环,当求解圆环轴线上距环心O为x处一点a的电势时,把带电圆环分割成许多可看作点电荷的电荷元,记每一个电荷元的电量为dq,每个电荷元到a点的距离均为r。

图2

2.3 计算曲线的长度

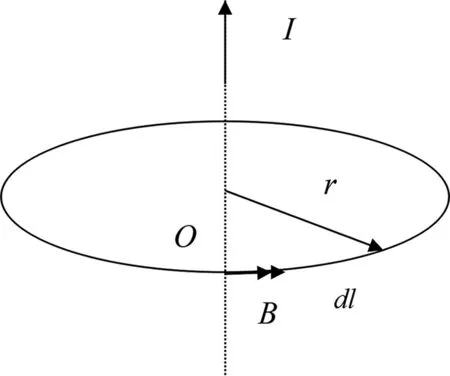
图3

3 大学物理教学与高等数学微分、积分教学的融合

高等数学对大部分理工科学生而言,学习过程中比较抽象,对学生的逻辑思维、运算能力有较高的要求,高等数学是顺利解决其他学科问题的重要工具,其中的函数极限和微积分部分是贯穿于高等数学中的重要内容,是整个高等数学学习的核心。当教师展开微分和积分教学时,需要教师在教学过程中引入大量生动的、形象的实例,帮助学生理解微分和积分公式所蕴含的意义,拓展学生思维,由浅入深、由简到难开展高等数学的教学,而大学物理中恰好有大量的实例可以参考和使用。

大学物理中关于微分和积分的生动实例比较多。除了上述详细介绍的实例,例如可以用微积分解决速度和加速度的问题,也可以解决质点的受力情况,即质点动力学中常见的两类问题,一类是已知质点的受力情况,求解质点的运动状态,此类问题通常可以用高等数学中的积分知识解决;另一类是已知质点的运动状态,求解作用于质点的力,此类问题一般用高等数学中的微分知识处理。此外,利用微积分知识可以处理物理学中遇到的变力做功问题,也可以解决不规则形状导体所受到的安培力及感应电动势的计算相关问题。

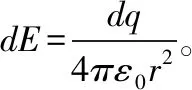
平时的大学物理教学中,作为授课教师应该从以下几个方面去挖掘高等数学中的微分和积分知识。第一,要熟悉大学物理中基本的物理模型,比如质点、刚体、弹簧振子等,熟悉这些基本的物理模型运动的特征。对于质点,不考虑其大小,但需要考虑质点的质量,在高等数学建立模型时,引入质点模型,会使得比较复杂的数学问题进一步简化。

图4

第三,作为大学物理授课教师,要能够向学生科学解释大学物理中微分和积分相关的公式所隐藏的本质和规律。麦克斯韦方程组全面地反映了电场和磁场的基本性质,真空中电磁场的四个基本方程形式如下:

(1)

(2)

(3)

(4)

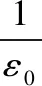
如果考虑空间存在磁介质和电解质,表达式(1)的形式变形为表达式(5),表达式(4)的形式可以变形为表达式(6)。

(5)

(6)

结语

结合上面的分析和探究,在大学物理平时的教学过程中,巧妙地引入高等数学中的微分和积分思想,利用微分和积分工具有效地解决了实际的物理问题,教师能够依据计算公式向学生阐释公式背后隐藏的物理本质及规律,从而体现了大学物理教学的严谨性、科学性和趣味性,更好地促进了大学物理教学。高等数学中的微分和积分思想应该被广泛地应用到实际的大学物理教学中,让微分和积分工具发挥更充分的作用。