梯度多孔介质腔体内固液相变过程数值研究

崔云杰陈宝明云和明随立言

(山东建筑大学热能工程学院，山东 济南 250101)

0 引言

相变储能技术作为一种有效的热存储技术，能够高效地解决能量在存储与释放过程中供需双方在空间、时间上的不匹配问题，因而广泛应用于建筑相变墙体[1]、太阳能供暖[2]、工业余热废热回收[3]等工业和民生的众多领域。 大量的研究工作集中于固液相变过程中的强化技术，如在相变材料中添加翅片[4]、纳米材料[5]、泡沫金属[6]等，可以有效弥补相变材料(如石蜡)导热率低、储热效率低的缺点。 由于实验研究测试的不准确性和不全面性，在揭示固液相变普遍规律时具有一定的局限性，传统的计算流体力学在解决这类问题时，复杂的边界与网格生成存在难以克服的缺陷，而具有介观特性的格子玻尔兹曼方法(Lattice Boltzmann Method， LBM)边界条件处理方便，在模拟复杂几何构造的问题时具有很大优势，已广泛应用于添加复杂金属结构的固液相变[7]、纳米材料增强凝固和融化过程[8]。

在相变换热过程中，添加多孔介质材料可以增强相变材料的蓄热能力，改善系统的温度均匀性。刘梓标等[9]将多孔介质复合相变材料与电池产热耦合，通过数值模拟与实验研究表明多孔介质能够加快相变材料融化，有效减缓电池产热。 ZHAO等[10]使用热格子(Bhatnager-Gross-Krook，BGK)模型来模拟多孔介质内二维流动与传热过程，研究了孔密度和孔隙率对自然对流的影响，表明了低孔密度与低孔隙率的多孔介质可以提高整体传热能力。TAO 等[11]利用LBM 方法数值模拟了泡沫金属/石蜡复合相变材料的相变蓄热过程，研究了均匀和非均匀泡沫金属结构对相变材料温度场、速度场、融化速率等的影响，得到了最佳的泡沫金属结构，并提出了增强传热性能的方案。 ABISHEK 等[12]利用开源工具构造不同微观结构的泡沫金属，从孔隙尺度模拟其对相变过程的影响。 WANG 等[13]使用多面体构造泡沫金属，对比不同材料的泡沫金属对复合导热系数的影响。

以上研究结果表明，相变材料中添加泡沫金属可以提高相变材料导热性能。 在众多泡沫金属结构的模拟研究中，四参数随机生长法(Quartet Structure Generation Set，QSGS)可以有效地与多孔介质格子玻尔兹曼方程(Lattice Boltzmann Equation，LBE)模型结合，达到数值构建与真实多孔介质高度匹配的效果，提高数值计算效率，因此常用来构造多孔介质。 HUANG 等[14]利用QSGS 生成二维多孔介质，采用基于焓法的LBM 求解了多孔介质内的相变过程，数值结果与实验结果吻合较好；李健等[15]通过改进QSGS 方法构造了三维复杂多孔吸液芯结构，在孔隙尺度下模拟毛细抽吸过程，孔尺度效应明显。

梯度多孔泡沫金属可以很好地改善整场温度均匀性，提高相变材料蓄热速率，对储能应用有着重要意义。 目前，有关梯度多孔介质在相变领域的研究多集中在二维模型，并不能充分反映三维孔隙结构。为了更好地掌握梯度多孔介质对相变过程影响规律，文章采用QSGS 生成三维方向梯度多孔介质骨架，从孔隙尺度求解含梯度多孔介质腔体内固液相变过程，讨论了方向梯度多孔介质对固液相变过程中相场分布、融化速率、热壁面平均努塞尔特数和温度场及速度矢量分布的影响。

1 物理模型

多孔介质骨架物理模型如图1 所示，研究对象为填充有梯度多孔介质骨架的相变材料。 方腔内蓝色部分代表多孔介质骨架，其余部分填充相变材料，左侧壁面设置为高温壁面无量纲温度Tm＝1，其余壁面均为绝热壁面。 多孔介质平均孔隙率为ε＝0.8，相邻孔隙率差值Δε＝0.05，梯度的变化是通过将方腔均分为3 个区域，区域内多孔介质孔隙率的数值依次增大或减小以实现负、正向梯度。 规定沿热量传递方向梯度的变化为x向梯度，垂直于热量传递方向梯度的变化为z向梯度。

图1 方向梯度多孔介质骨架模型

2 数学模型

相变材料的相变过程根据状态不同可分为固相区、液相区和糊状区。 其中，糊状区的发展迁移规律和传热传质特性对整个固液相变过程有着重要影响。 文章基于CHEN 等[16]提出的固液相变糊状区“多孔介质-多相流”两区域模型，对含梯度多孔介质骨架固液相变过程建立数学模型，并对数学模型作如下假设:(1) 液相区的相变材料为不可压缩流体，流动方式为层流；(2) 液相区和糊状区中产生的自然对流效应满足Boussinesq 假设；(3) 多孔介质骨架和相变材料的物性参数均为常数；(4) 忽略相变过程中的体积膨胀效应。

2.1 控制方程

基于三大守恒定律建立对应的连续性方程、动量方程和能量方程，分别由式(1)～(3)表示为

式中u为渗流速度；t为时间；p为表观压力；r为含液率；ρeff为相变材料有效密度；μeff为有效动力黏性系数；(ρCp)eff为有效热容；Tf为液相相变材料温度；keff为有效导热系数；La为相变潜热；F为含线性、非线性及浮升力的总体积力项，由式(4)表示为

式中vfl为液相相变材料的动力黏性系数；Fε为多孔介质的形状因子；βT为液相相变材料的热膨胀系数；K为多孔介质的渗透率；g为重力加速度；T为温度；Tref为参考温度。

在液相区不发生相变过程，即r＝1，上述控制方程可表示为耦合自然对流的流动传热方程。 在固相区r＝0，通过设置速度和压力为0，上述方程可表示为相变导热的控制方程。

在糊状区的低含液率区域，表现出多孔介质渗流的特性，其有效导热系数和渗透率由式(5)和(6)表示为

式中kfs、kfl分别为固相和液相相变材料导热系数；C为糊状区常数，其值为1 600。

在糊状区的高含液率区采用多相流模型的表征参数法，通过多相流模型的经验或半经验公式表征多相流区的流动与传热特点。 表征导热系数、表征运动黏度可由式(7)～(9)表示为

式中(keff)w为两者之间不存在相对运动时的有效导热系数；kd为热扩散作用导致的系统导热系数的增强系数；μf为液相相变材料的运动黏度系数；φ为固相相变材料的体积分数，即φ＝1-r。

为了深入探讨梯度多孔介质对固液相变影响的一般性规律，引入无量纲变量，通过将参数无量纲化可减少控制方程的变量，其相关参数为:

其中，Th、Tc分别为高温、低温壁面温度；L为特征长度；ρfl为相变材料液相密度；αfl为液相相变材料的热扩散系数；Fo、Pr、Ra、Da和Str分别为无量纲时间傅里叶数、普朗特数、瑞利数、达西数和斯蒂芬数；σ为热容比；R为导热系数之比。

2.2 LBM 方法

采用双分布LBM 方法D3Q19 模型求解，模型中对应的速度、温度演化方程及平衡态方程分别由式(10)～(13)表示为

模型中速度与温度方程中的无量纲松弛时间由式(16)和(17)表示为

式中ν为有效黏性系数；αs为温度膨胀系数。

流体的宏观参数密度和速度由(18)表示为

由于总体积力项F中含有流动速度u，因此式(18)是速度的二次非线性方程式，引入临时速度V，可得式(19)和(20)为

3 网格无关化及模型验证

3.1 网格无关化验证

为满足计算精度和节约计算资源，模拟过程需要选择合适的网格数量。 在无量纲参数Pr＝1、Ra＝1×105、Ste＝5、骨架与相变材料导热系数比Rs＝100时，模拟网格数分别为63×63×63、81×81×81 和99×99×99 的含梯度多孔介质骨架的相变过程，工况选择为x向负梯度，相邻孔隙率差值Δε＝0.05。 取液相分数Vf/V＝1 时对应的时间为完全融化时间，则不同网格数对应的完全融化时间见表1。 随着网格数量的增加，相变材料完全融化时间相对增加了2.6%和3.9%，认为网格数量的增加对计算准确性影响较小，考虑到多孔介质结构的复杂性及计算涉及孔隙流动，最终选定81×81×81 为计算网格数，既满足结果的准确性又节约成本。

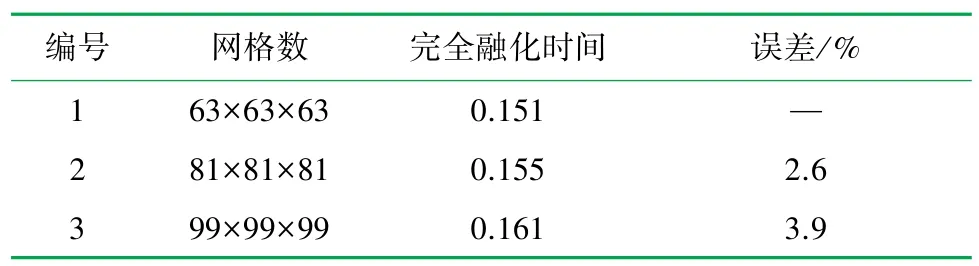
表1 网格无关化验证

3.2 模型自然对流验证

在固液相变过程中，自然对流作用的存在致使相变过程复杂，该问题到目前为止仍没有公认的基准解。 为了验证模型的正确性，采用包含自然对流作用下相变换热热壁面Nuave和Ra数等参数的关联式[17]，由式(21)和(22)表示为

模型中左壁面为高温壁面(温度为Th)，右壁面为低温壁面(温度为Tc)，其余4 个壁面为绝热壁面，物性参数为Pr＝5、Ste＝0.1，Ra依次为为1×104、1×105和1×106。 将纯相变模拟计算结果与经典解进行对比，结果如图2 所示。 文章提出的三维LBM模型与经典解吻合较好，由此验证了耦合自然对流相变模型的正确性。

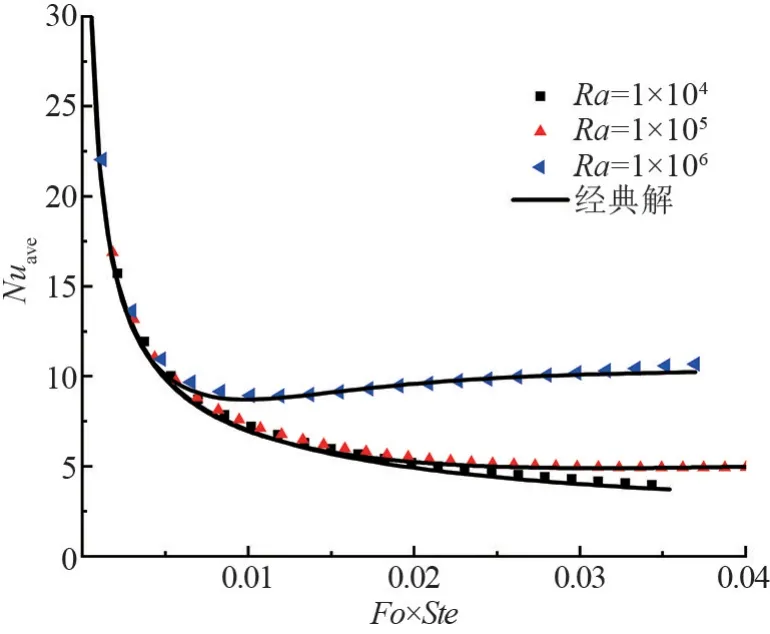
图2 耦合自然对流数值解与经典解对比图

3.3 模型流固耦合验证

由于涉及多孔介质内固液相变，多孔介质与液相相变材料的流动换热在相变过程中有着重要影响，必须正确处理流固耦合关系。 简化计算模型，方腔内存在边长为方腔边长一半的正方体，代表多孔介质骨架，方腔左侧为高温壁面Th，右侧为低温壁面Tc，其余壁面为绝热壁面，物性参数设置为Pr＝0.71，Ra取1×103、1×104、1×105和1×106，计算不同Ra数工况下左侧壁面Nuave，并对比计算结果与文献[18-19]结果，如图3 所示。 模型计算数值与经典解吻合较好，可以认为文章建立的含多孔介质固液相变模型流固耦合的正确性。

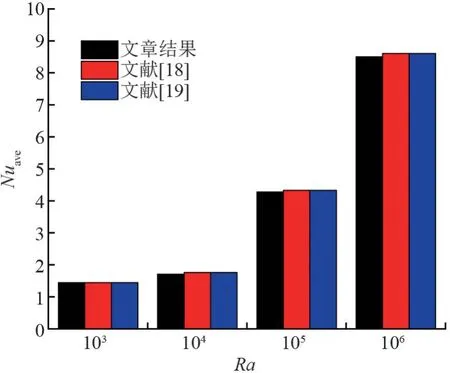
图3 流固耦合数值解与经典解对比图

4 结果与讨论

基于孔隙尺度对含方向梯度多孔介质的相变过程数值模拟，设置参数为Pr＝1、Ra＝1×105、Ste＝5、骨架与相变材料导热系数比Rs＝100，梯度多孔介质的构建采用QSGS 生成。 定义多孔介质孔隙率沿x轴正方向由低到高为正梯度(∇x＋)；孔隙率沿x轴正方向由高到底为负梯度(∇x-)，同理规定z方向的正、负梯度(∇z＋、∇z-)。 在添加多孔介质骨架的相变过程中，骨架的存在对相变过程有着双重影响:(1) 多孔介质骨架可以提高相变材料的有效导热系数，增强传热性能；(2) 骨架的存在抑制了液态相变材料的自然对流，从而削弱了传热性能。 因此，对相变过程的讨论要综合热传导与热对流[20]。

4.1 方向梯度对固液相变相场分布的影响

无量纲时间Fo分别为0.02、0.06、0.10 和0.14时，不同方向梯度方腔内相场分布如图4 所示，红色部分为液相相变材料，对应液相分数为1；蓝色部分为固相相变材料，对应液相分数为0，介于红色和蓝色之间的状态为糊状区。 在相变初期(Fo＝0.02)时，不同工况相变材料融化时固液相界面近乎平行于加热壁面，且有着相对较薄的糊状区，此时热量传递方式表现为多孔介质骨架的导热，靠近加热面骨架数量排布越密集的工况导热效果越好。 由图4 可以看出x负梯度液相区最多，其次为x正梯度，随后是z向梯度。 相变中期时(Fo＝0.06、Fo＝0.10)，由于已融化的相变材料增多，会使导热热阻增大，阻碍了导热的进行，使其能力降低的同时自然对流作用开始显现并逐渐占据主导地位。 在此阶段已融化相变材料受到浮升力作用向方腔顶部移动，热量在上部堆积，加快相变材料融化，形成上窄下宽的糊状区。x向正梯度与z向正梯度有着较为倾斜的糊状区，此阶段抑制了方腔内骨架导热，自然对流作用增强。x向负梯度糊状区倾斜程度小，骨架的导热在推进固液相界面移动时起主要作用。 在相变后期(Fo＝0.14)，x、z向正梯度方腔内的相变材料在右下角堆积，这种现象主要由于自然对流较强时，糊状区倾斜，液相相变材料自上而下冲刷所致。 堆积的相变材料由于较小的换热面积不利于对流换热，从而减缓融化速率。x向负梯度骨架导热作用强，堆积现象不明显，液相分数大；z向负梯度有着与z向正梯度相反的骨架分布，避免了相变材料过多堆积，同时低孔隙率骨架集中在方腔底部更有利于底部相变材料的融化，相同时刻有着更大的液相分数。

图4 不同方向梯度方腔内相场分布图

多孔介质骨架可以阻碍液相相变材料的流动，进而影响相变材料的对流换热，掌握多孔介质之间的流体流动特性对揭示自然对流作用影响固液相变过程的规律有重要意义。Fo＝0.11，x向正梯度在y＝0.5截面处的液相分布如图5 所示，并选取了靠近热壁面处与糊状区的局部速度矢量图，图5(a)和(c)中黑色箭头代表该位置处速度的大小与方向。热壁面处相变材料温度升高，受浮升力影响向上运动且高速流体多集中在骨架空隙处。 流经骨架时速度方向改变，流速降低，骨架的存在抑制了主流区的形成，削弱了自然对流作用。 靠近糊状区与糊状区内低含液率部分温度低，流速小，受重力影响沿骨架向下运动，造成低温相变材料在方腔底部堆积。

4.2 方向梯度对固液相变速率影响

x、z方向正、负梯度，相邻孔隙率差值Δε＝0.05时，液相分数Vf/V随无量纲时间Fo的变化曲线如图6 所示。 相邻孔隙率差值Δε＝0.05，x向负梯度相变材料的融化速率高于x向正梯度。 相变初期固相相变材料受高温壁面影响开始吸收热量，此时热量传递方式以导热为主，相变中后期随着液相相变材料增多，自然对流作用逐渐增强并占主导地位。对比x向正、负梯度骨架的孔隙率排布，x向正梯度靠近热源侧孔隙率高，骨架数量少，相变初期导热量少；远离热源侧孔隙率高，骨架分布密集，相变中后期自然对流作用开始显现时，受到骨架抑制作用强烈，对流换热效率低；x向负梯度骨架排布与正梯度相反，靠近加热面骨架密集，相变初期有效导热系数大，导热量多，加快相变材料的融化，促进自然对流的形成，而远离热源侧骨架稀疏，对自然对流的抑制作用低，在相变中后期表现出更快的融化速率。 因此，x方向负梯度的骨架更有利于促进相变过程的进行。 相变后期z向负梯度的融化速率高于z向正梯度。 无论是z向正梯度还是负梯度，靠近左侧高温壁面的骨架数量相同，意味着相变初期骨架导热能力基本相同，融化速率相同。 但相变后期对于z向正梯度，低孔隙率的骨架集中在方腔顶部，意味着顶部相变材料的融化快于底部，会使低温相变材料向底部堆积，形成“角化”现象，造成相变后期融化速率减慢；z向负梯度时，低孔隙率骨架集中在方腔底部，通过热传导可以加快底部相变材料融化，同时顶部稀疏的骨架分布对自然对流的扰动作用小，也会使z向负梯度有着更快的融化速率。

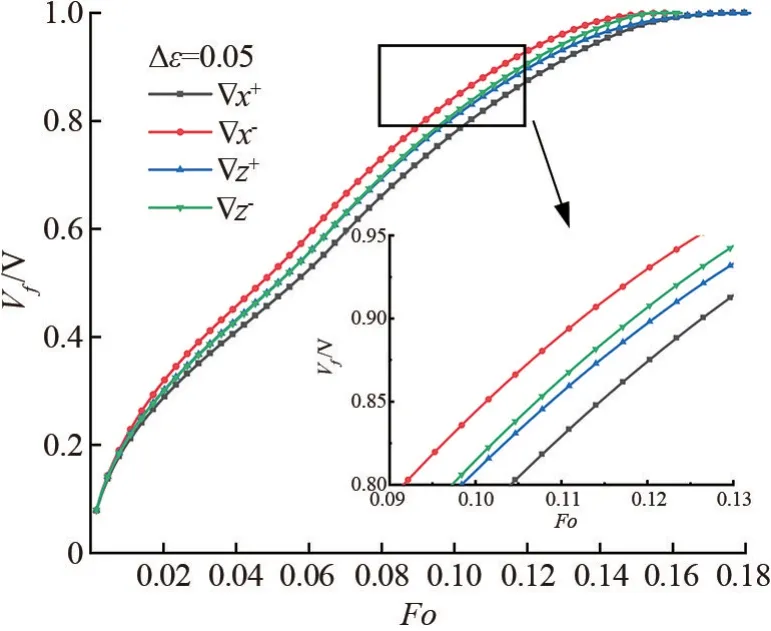
图6 Δε＝0.05 时，液相分数Vf/V 随Fo 的变化图

热壁面平均努塞尔特数Nuave反映热壁面处温度梯度的大小，常被用来表征系统热壁面换热能力，为了综合分析多孔介质骨架对相变过程的影响，引入左壁面Nuave，其值随无量纲时间变化曲线如图7所示。 不同工况左壁面Nuave随时间变化趋势相同，相变初期壁面处温度梯度最大，随着相变材料温度升高，温度梯度逐渐减小，而后趋于平缓，自然对流作用开始显现。 可以看到相变后期x向正梯度左壁面Nuave最大，其次为z向正梯度，表明导热作用降低时x向正梯度的对流换热能力略优于z向正梯度；x向负梯度左壁面Nuave小于z向负梯度，说明x向负梯度骨架导热优势明显高于z向负梯度；同时z向正梯度对流换热能力优于z向负梯度。

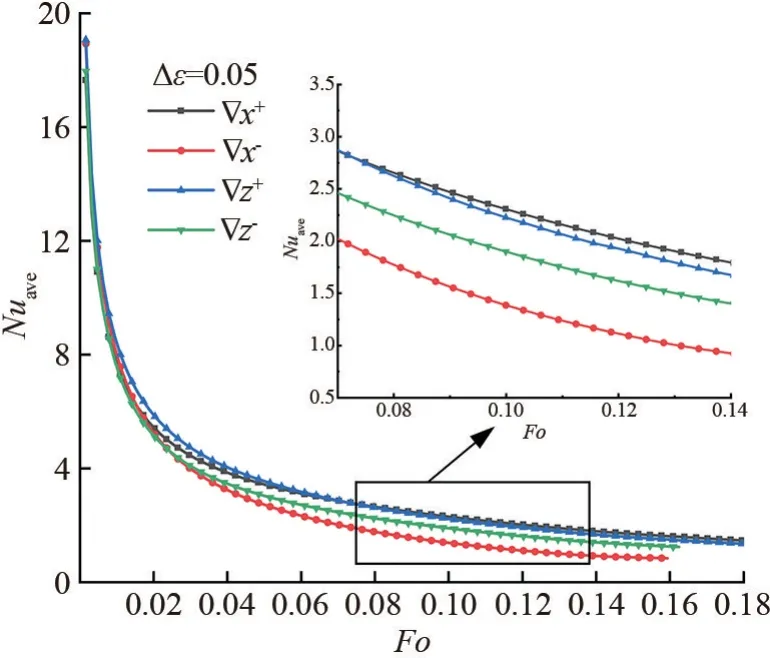
图7 不同方向梯度左壁面Nuave随Fo 变化图

4.3 相邻孔隙率差值对固液相变过程的影响

文章构建的梯度多孔介质骨架，通过改变相邻骨架孔隙率差值的大小，可以达到改善或抑制方腔内局部的导热与对流作用，对整场的温度、速度分布有一定的影响。 相邻孔隙率差值Δε在0.03、0.05和0.08 时，不同方向梯度的液相分数Vf/V随时间Fo的变化曲线如图8 所示。 可以看出，随着Δε的改变x向梯度变化明显，z向梯度变化小。 表明相变材料的相变过程受到孔隙率变化带来的响应程度在沿热量传递方向要大于垂直热量传递方向。 Δε的增大，就x向负梯度而言，意味着靠近加热面骨架数量增多，有效导热系数增加，热量传递效率更高，融化速率更快；对于x向正梯度，靠近高温壁面骨架数量减少，有效导热系数减小，热量传递效率低，同时相变后期骨架数量的增多抑制了自然对流，从而融化速率降低；z向正梯度方腔顶部骨架数量增多虽然加快了顶部热量传递，但自然对流的增强使相变材料过多堆积，不利于相变后期固液相界面推进。相对的z向负梯度方腔底部骨架数量增多，加快了底部热量传递，同时顶部骨架的减少对流动阻碍作用减弱，以上共同作用使得融化速率加快。

图8 不同方向梯度液相分数Vf/V 随无量纲时间Fo 的变化图

等温线与速度矢量分布可以反映出骨架导热的作用与对流动的扰动情况，对于探究梯度多孔介质对固液相变过程的影响研究有重要意义。 相邻孔隙率差值Δε＝0.03、0.05、0.08，无量纲时间Fo＝0.11时，不同方向梯度在y＝0.5 切面处的等温线与速度矢量图如图9 所示。 图中红色箭头表示该位置处相变材料的速度大小及方向，蓝色线条为等温线，不规则的环形区域为多孔介质骨架，红色到黑色区域为液相分数从0.05 到0.70 范围内的低含液率区，其形状与大小受骨架导热与液相相变材料对流换热影响。

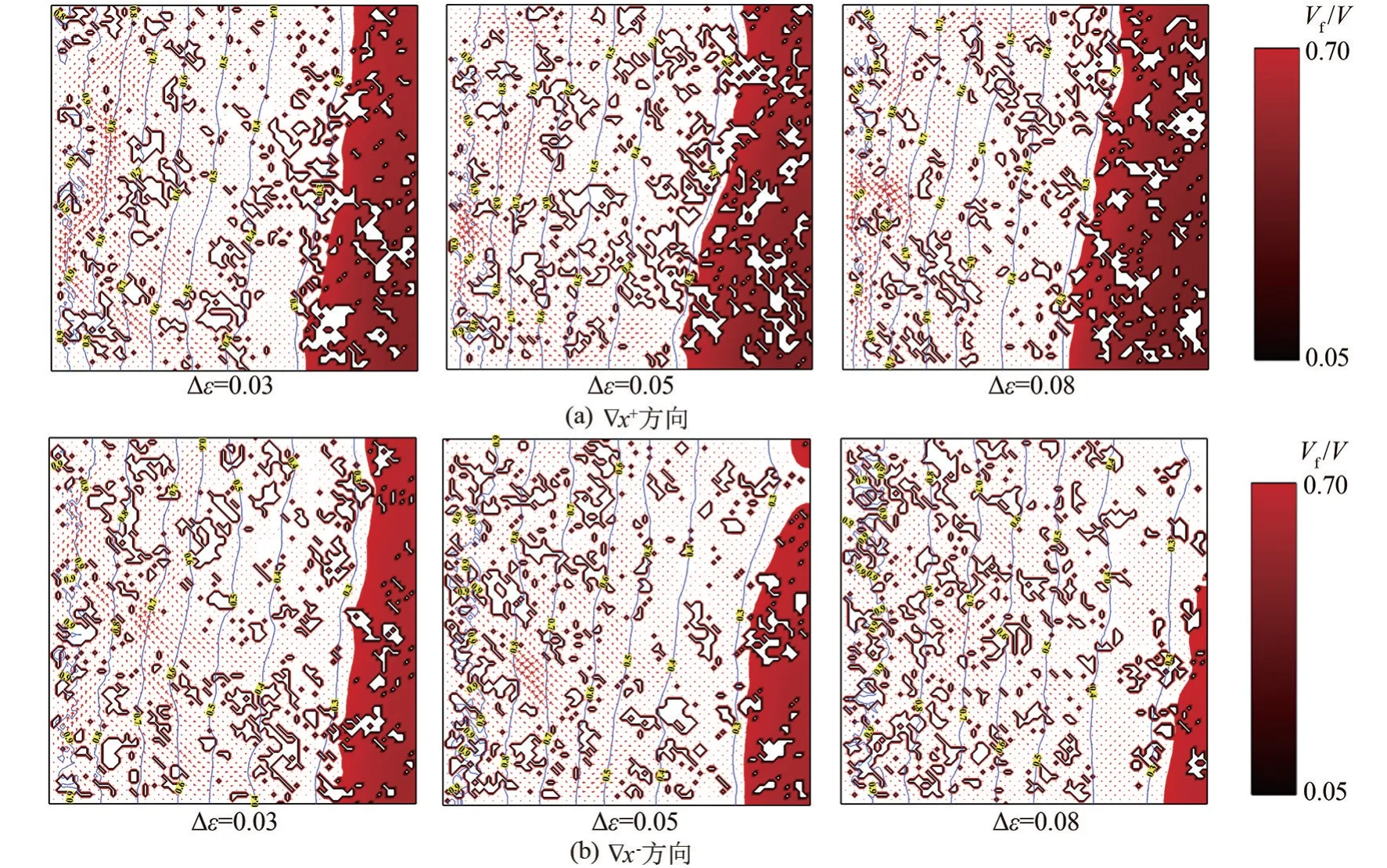
图9 不同方向梯度在y＝0.5 处等温线与速度矢量图

随着Δε的增大，x向正梯度温度梯度增大，等温线向右倾斜的程度增大，已融化相变材料流动速度提高，自然对流作用增强，但靠近高温壁面处骨架数量减少，有效导热系数减小，融化速率减慢；x向负梯度等温线倾斜程度减小，骨架导热作用增强，速度分布更加分散且主流区流速降低，自然对流作用减弱；z向正、负梯度等温线与低含液率区分别向右下和右上倾斜，且主流区均向高孔隙率骨架处集中，Δε的增大分别增强了顶部和底部骨架的导热能力，使糊状区形态发生改变。

5 结论

基于LBM 方法，分析了方向梯度对固液相变相场分布及融化速率的影响，探究了相邻孔隙率差值的改变对相变材料融化过程影响规律，所得主要结论如下:

(1) 对于相变材料融化速率，梯度多孔介质x向变化对其影响大，而z向的变化影响小。

(2)x向负梯度高温壁面处多孔介质密集，导热作用强，融化速率快，糊状区较薄；x向正梯度高温壁面处多孔介质稀疏，导热作用弱，热量传递依赖自然对流作用，使得糊状区较厚且倾斜程度增大，热量传递效率变低，融化速率减缓。

(3)z向负梯度方腔底部多孔介质密集，强化传热，相变材料融化速率加快；z向正梯度顶部孔隙率小，导热作用强，糊状区倾斜程度明显，相变材料容易堆积，融化速率更慢。

(4) 相邻孔隙率差值的增大，x向负梯度相变材料融化速率更快，竖直方向温度更加均匀；x向正梯度融化速率降低，骨架导热能力减弱。z向正梯度融化速率降低，竖直方向温度不均匀性增大，相变材料更容易堆积；z向负梯度融化速率加快，可以有效改善相变材料堆积产生的换热效率低的问题。