基于LCL补偿的双频双负载无线电能传输系统

夏锦涛,沈艳霞

(江南大学 物联网技术应用教育部工程研究中心,无锡 214122)

0 引 言

无线电能传输(以下简称WPT)技术因其方便、安全的优势,被越来越多地应用于医学设备、电子设备、交通工具等领域[1]。随着WPT技术的日益普及,用户侧的设备需求呈现出不同频率、不同功率等复杂多样的特点。为了满足上述用户侧复杂多样的需求,多接收机WPT系统已成为当前WPT技术研究的重点之一。基于无线充电联盟提出的Qi充电标准[2]的紧耦合感应技术,以及基于AirFuel组织的松散耦合磁谐振技术[3],已经被逐渐应用于多接收机WPT系统中,可以满足对于不同充电标准的负载设备的供电需求。文献[4-5]对多负载磁耦合谐振无线功率传输(以下简称MCR-WPT)系统的基本原理进行了详细的介绍。

多接收机WPT系统可分为单频多接收机WPT系统和多频多接收机WPT系统。单频多接收机WPT系统中发射电路与接收电路处在同一谐振频率下[6],传输至不同接收机负载上的功率均通过同一谐振频率通道进行传输,因此不同负载得到的功率是由自身接收机谐振电路参数决定的,无法重新进行分配,且传输效率易受到接收线圈间交叉耦合的影响。

在采用多逆变器的多频多负载WPT系统中,通过控制每个逆变器的开关信号占空比,可实现接收机的功率分配。如文献[7]采用全桥逆变器的多对多线圈耦合方式,却增加了系统的体积与成本。文献[8]利用变压器将多个半桥逆变器输出的频率信号耦合叠加传输到发射线圈,但带来了变压器损耗。为此,文献[9]通过控制单逆变器两桥臂工作在不同的开关频率,实现双频混合输出,在实现多负载功率分配的同时避免了以上问题。文献[10]则通过对电流进行谐波分析,采用固定开关频率调制方法利用单个逆变器产生的谐波频率。文献[11]将多谐波电流进行叠加,输出类正弦电流,但其输出频率和幅值都受到谐波阶次的限制。针对上述问题,文献[12]将不同频率和幅值的正弦电压信号进行叠加,调制得到包含不同信号波形信息的逆变器开关信号,控制输出多频功率信号。文献[13]将这种混合调制波引入于多频MCR-WPT系统中,但因发射线圈采用零补偿结构,系统存在无功功率,增加了系统损耗。

本文提出了一种双频双通道MCR-WPT系统,采用多频多幅叠加调制方法实现全桥逆变器的控制,利用LCL补偿拓扑为系统建立两个独立的功率传输通道。为实现氮化镓(GaN)开关管的零电流开关(以下简称ZCS)以减少系统开关损耗,基于粒子群算法对LCL拓扑中的最优串联电感及并联补偿电容寻优,将系统的两个自然谐振频率点设计在期望谐振频率附近,使对应谐振频率的接收机获得较大的功率,并且能实现不同负载间功率的分配调节。

1 双频双通道WPT系统结构

图1为一种双频双通道MCR-WPT系统,主要包括电源、LCL补偿网络以及接收机。该系统采用多频多幅(以下简称MFMA)叠加法将双频信号调制后通过单逆变器输出,输出两个频率的功率信号。尽管LCC/S[14]、LCL/S[15]、LCC/LCC[16]等补偿拓扑分别具有恒压输出、零电压开关(以下简称ZVS)、耦合系数无关等特性,但考虑本文需要建立两个功率通道来进行传输,就需要有两个自然谐振频率,因此选择LCL补偿拓扑。两个接收机采用串联电容器补偿,利用传统的不可控整流器和并联滤波电容器对接收信号进行交直流转换。

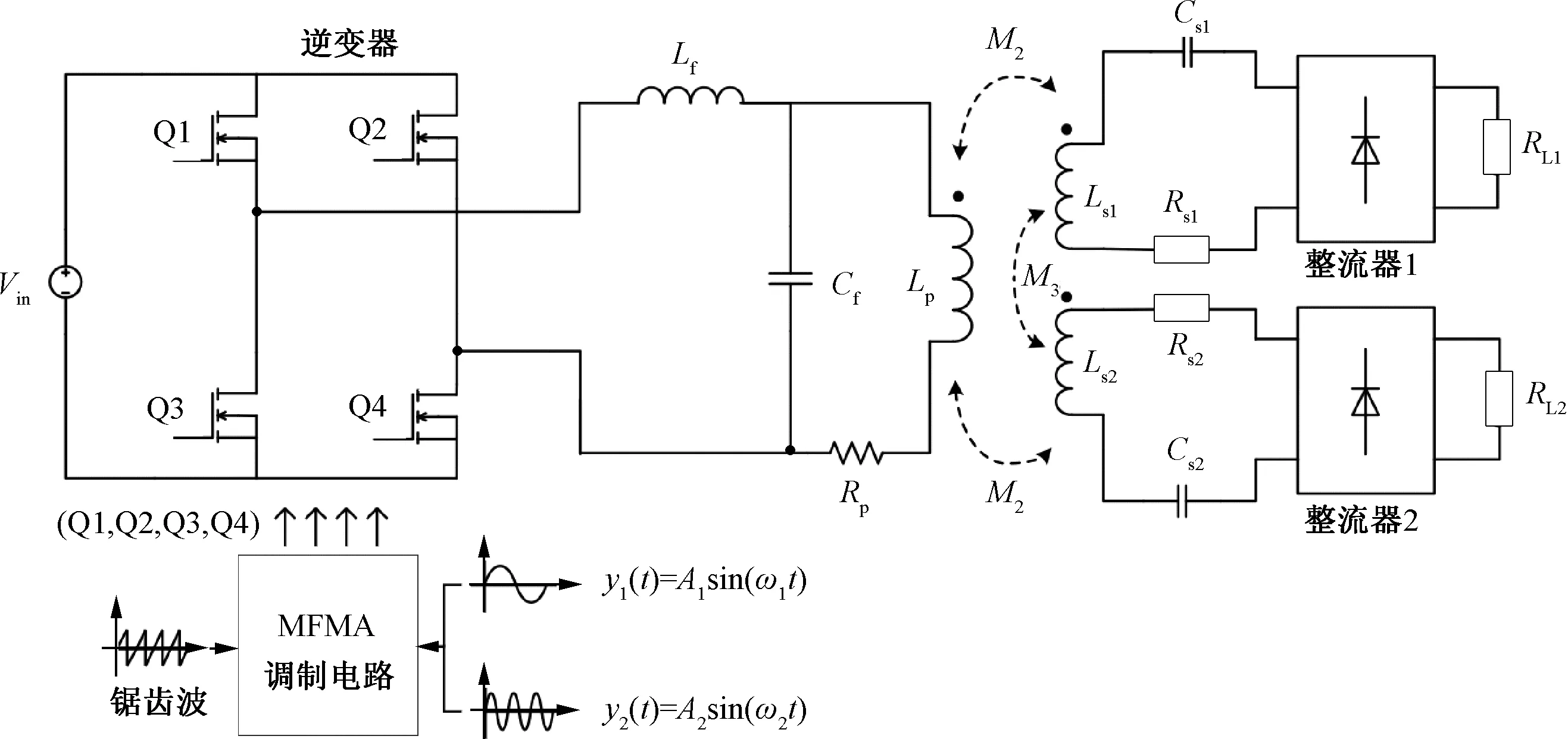
图1 双频双通道MCR-WPT系统

图1中,Lf为基本LCL拓扑的第一电感,Cf为基本LCL拓扑的并联补偿电容,Lp为基本LCL拓扑中发射侧线圈的自感,Ls1和Ls2为两接收机线圈的自感,Cs1和Cs2为两接收机并联补偿电容,M1和M2分别为发射线圈与两接收线圈之间的互感系数,M3为两接收线圈间互感系数,Rp和Rs1以及Rs2分别为发射线圈和接收线圈的等效串联电阻,为简化后续计算,在模型分析中将其设置为常数,RL1和RL2分别为两负载阻值。

图1为系统采用MFMA叠加调制方法的逆变器结构。通过两对互补的控制信号(Q1与Q4,Q2与Q3)控制基于GaN的全桥逆变器开关管的通断时间,实现多频信号叠加输出,在输出的方波信号中,包含多个不同频率、不同幅值的正弦波信号。

将两种不同频率、不同幅值的正弦波信号在时域上进行叠加,得到包含两种正弦波信息的混频信号,其表达式:

(1)

式中:y1(t),y2(t)为不同频率、不同幅值的正弦波信号;A1,A2分别代表两种正弦波信号归一化后的电压幅值。与SPWM方法类似,将两种信号的混频信号与高频锯齿载波进行比较,分别输出高电平与低电平来控制两对互补的全桥逆变器开关管。同时,可以通过改变两种正弦波信号的电压幅值,来调节输出信号功率比。

为了实现较好的等效效果,锯齿载波频率需要足够大,能够承受比较器输出的高频方波控制信号。考虑到混频信号的正、负半波特性,采用双极性调制优于单极性调制。上述MFMA叠加调制法原理简单,且易于实现,叠加频率可选范围较广,适合应用于多频多通道WPT系统。

同时,为减少在高频条件下逆变器的开关损耗,开关管也必须实现ZCS。GaN开关管作为新一代高性能宽禁带半导体器件,现已逐渐广泛应用于电力电子行业中,与传统Si开关管相比,GaN开关管具有如下优势:在相同面积下,导通电阻RDS(ON)是Si开关管的一半,可使电路中传导损耗降低一半;具有较低的输出电荷COES,开关损耗下降多达80%,应用在实际电路中可以提高效率,减少开关管的发热,减少散热器的体积;具有较低的栅极电荷QG,不存在反向恢复过程,可以工作在更高的开关频率;具有更大的禁带宽度,可提高系统工作的可靠性。本文采用GaN开关管作为逆变器的导通关断元件。

2 系统建模分析

为了分析系统在不同频率下工作的阻抗特性,采用基波分析法将双频双通道MCR-WPT系统等效为两个单一频率电源输入、拓扑结构完全相同的等效电路,如图2所示。

图2 基于基波分析法的电路等效模型

2.1 双频双通道MCR-WPT系统的数学模型

(2)

式中:A1和A2表示对应频率信号电压的归一化幅值。

不可控整流器与负载的等效负载Req1和Req2可以表示[8]:

(3)

利用基尔霍夫电流定理和基尔霍夫电压定理,建立如下的双频一对二WPT系统模型矩阵:

(4)

式中:

(5)

(6)

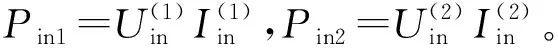
由于电路采用LCL高阶补偿网络,对电路理论矩阵求解得出的电流公式非常复杂,通过计算电流电压特性来分析系统的输出功率和传输效率很困难,即很难直接通过计算关系调节系统参数来实现高效率传输。因此可具体分析系统的输入阻抗与频率关系,通过智能寻优算法,对系统参数进行设计,建立合适频率的功率通道进行能量传输。

2.2 系统输入阻抗频率特性分析

如图5所示,在某一工作频率时,接收机1与接收机2在发射侧的反射阻抗分别为Zr1(i)和Zr2(i),其谐振频率分别为fs1和fs2:

(7)

(8)

接收机在各自的谐振频率点时,其反射阻抗为纯电阻负载。在此频率下两接收机在发射侧的总反射阻抗:

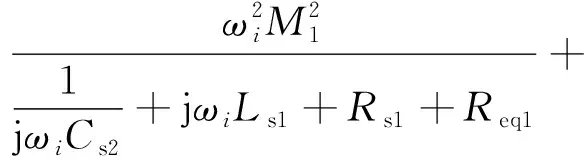
(9)

此时系统的输入阻抗可以表示为

(10)

由于系统的工作频率较高,且采用MFMA方法对双频信号进行调制,因此对于基于GaN的全桥逆变器来说,开关管的ZCS是必要的,需要确定使系统工作在零相位角(以下简称ZPA)的频率,即整体系统的自然谐振频率。若将式(9)化为实部与虚部的形式,令Zin虚部为0,得出的算式是关于谐振角频率ωi的隐函数,其解析解是无效的,而利用数值解得出的结果也较为复杂。因此,通过绘制系统输入阻抗角的频率特性图来寻找系统自然谐振频率点。一般来说,系统中的Lp,Ls1,Ls2,Cs1,Cs2,RL1,RL2等参数都是事先固定的参数,可通过调节发射侧LCL拓扑中的第一电感Lf以及并联补偿电容Cf来使系统工作在ZPA,以实现ZCS。

3 粒子群算法设计系统参数

为了让接收机获得较大的功率,需要建立合适的功率传输通道,即系统的两个自然谐振频率尽可能靠近接收机的自然谐振频率,且接收机的自然谐振频率可根据实际应用需求进行调整,提高其泛用性,需要自适应调整系统参数。由于直接确定变量Lf与Cf来建立高功率双频传输通道是有难度的,因此本节利用粒子群算法对系统的参数进行设计,以实际谐振频率fai与目标谐振频率fei之差为适应度函数,同时考虑功率平衡问题,即输出电流Isi平衡问题,寻找最优的Lf、Cf参数来提高系统双频双通道传输效率,达到根据实际需求快速准确设计系统的目的。具体算法过程如下:

计及功率平衡的谐振频率粒子群寻优算法的步骤如下。

输入:Lp,Ls1,Ls2;Cs1,Cs2;Rp,Rs1,Rs2;RL1,RL2;M1,M2

2)设定粒子Lf和Cf的取值范围和运动速度范围:Lmin,Lmax,Cmin,Cmax,VLmin,VLmax,VCmin,VCmax

3)设定惯性权重w,自我学习因子c1,群体学习因子c2,迭代次数ger,当前代数iter

4)初始化Lf与Cf种群粒子的位置L与C,速度以及粒子个数N

5)设计函数F(Lf,Cf),可根据系统参数计算出谐振频率fa1,fa2

6)whileiter<=gerdo

7)fori=1∶Ndo

8)计算每个粒子的适应度fx(i);

9)更新个体最佳适应度fxm,个体最佳粒子xm

10)更新群体最佳适应度fym,群体最佳粒子ym;

11)记录最佳适应度对应的频率fam1,fam2

12)end for

13)更新粒子的速度:

vL=vL·w+c1·rand·(Lm-L)+c2·rand·(YLm-L)

vC=vC·w+c1·rand·(Cm-C)+c2·rand·(YLm-C)

14)更新粒子位置L,C

15)迭代次数iter=iter+1

16)end while

输出:Lf,Cf,fam1,fam2

系统LC参数与系统输出电流Isi优化过程如图3所示,目标函数Fitness优化过程如图4所示。系统LC参数的最优值与目标函数的最小值在算法迭代至第226代时产生。第一代Fitness的值远大于10 000,在经过算法优化后,其值降低至153.1,效果较为显著。粒子优化结果分别为Lf=74.17 μH,Cf=99.74 nF,即全局最优值。从粒子优化过程图与目标函数寻优过程图可以看出,粒子群算法能在较大程度上优化粒子,使系统实际谐振频率无限接近期望谐振频率,同时,各接收机输出电流无限接近一致。

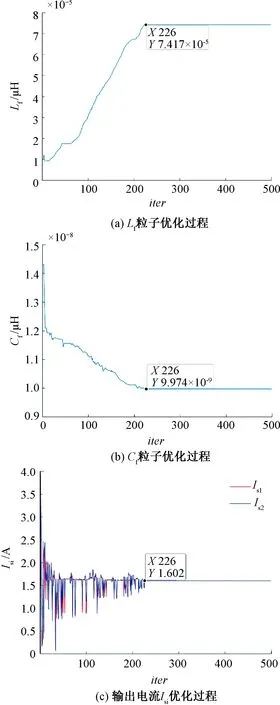
图3 计及功率平衡的系统参数优化过程

图4 计及电流的目标函数优化过程

4 系统仿真与实验

4.1 系统仿真

基于 MATLAB对本系统及参数设计粒子群算法进行仿真,仿真用参数如下:Vin=100 V;Lp=Ls1=Ls2=100 μH;Lf=74 μH;Cf=10 nF;Cs1=8 nF;Cs2=5 nF;Rp=Rs1=Rs2=0.1 Ω;RL1=RL2=10 Ω;M1=M2=50 μH。

图5为系统输入阻抗Zin与输入阻抗角φ的频率特性图。

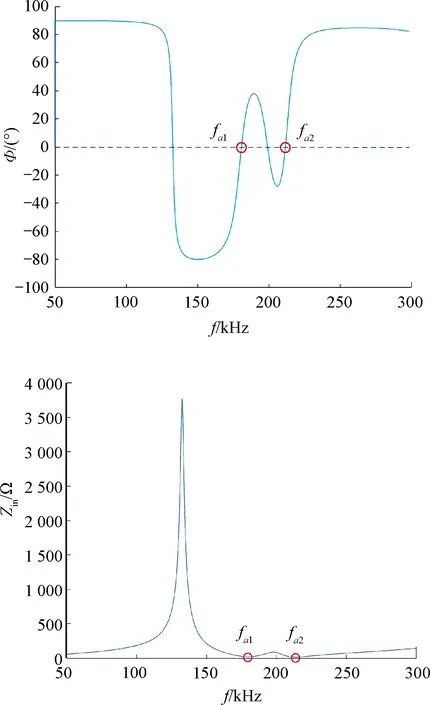
图5 系统输入阻抗与输入阻抗角频率特性

图5中,频率为fa1与fa2时对应系统输入阻抗由容性阻抗转为感性阻抗的零相位角点,其对应的系统输入阻抗最低。然而,当系统输入阻抗由感性阻抗转为容性阻抗时,其零相位点对应的系统输入阻抗极高且极不对称,无法建立合适的双频率功率通道。因此,根据上述特性,选取系统自然谐振频率点,以此建立双频功率传输通道,同时实现GaN开关管ZCS,使系统工作在ZPA点。

由系统输入阻抗角频率特性图,确定两个正弦调制波频率分别为180.7 kHz和211.5 kHz,将其幅值设定为三组,第一组为A1=A2=0.5,第二组为A1=0.75与A2=0.25,第三组为A1=0.5与A2=0.4。

图6是三组正弦调制波不同幅值下的两个接收机输出电压波形。系统输出电压比与正弦调制波幅值比大致相同,传输效率η保持在80%左右。基于MFMA叠加调制法的多频MCR-WPT系统可以实现在多个频率通道同时进行功率传输,并且可以独立调节单一频率通道传输功率。

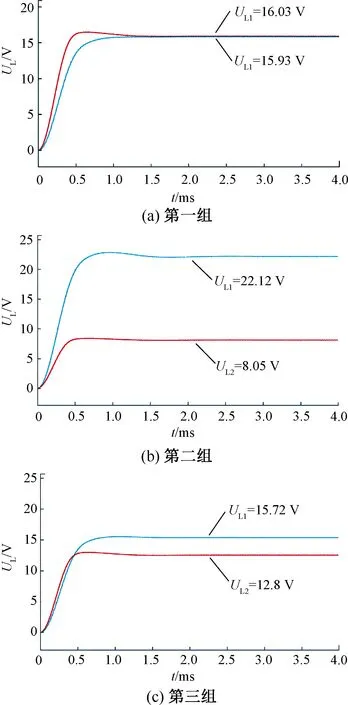
图6 接收机输出电压

4.2 实验验证

搭建实验样机对上述提出的双频双通道MCR-WPT系统及参数设计方法进行验证。如图7所示,实验系统采用普源RIGOL公司DG1062Z型号的函数任意波形发生器作为信号源,产生MFMA叠加调制信号。利用超高速电压比较器将该调制信号生成对应的反相信号。考虑到逆变器工作在高频开关状态,而常规Si器件,例如MOS管,其开关频率仅在100 kHz以下,不满足系统工作的开关频率要求。因此,采用基于GaN开关管的逆变器,其工作频率可达兆赫兹级别。

图7 实验样机

因发射和两接收线圈间的相互耦合包括两个接收线圈间的交叉耦合,为双频双负载MCR-WPT系统的输入能量提供了错综复杂的传输通道,在系统输入双频叠加信号时,负载功率会受到接收线圈间互感的影响,且由两个频率能量叠加所得。因此,本文实验系统对传统同轴线圈放置方式进行改进,将双接收线圈平行放置,发射线圈轴心位于两接收线圈轴心连线的中点位置,此方式可直接消除接收线圈间交叉耦合。

实验参数如表1所示,实验结果如表2所示。

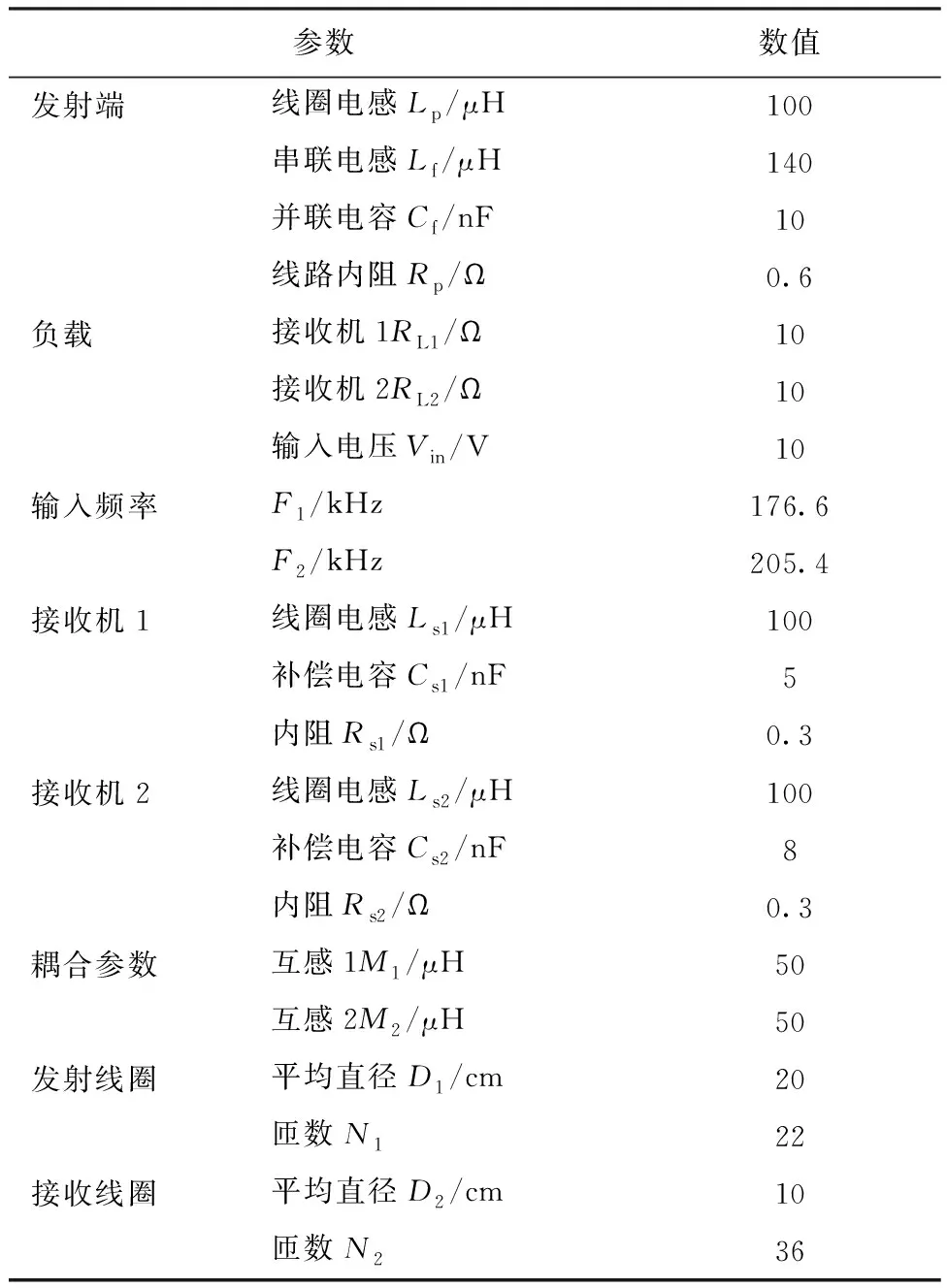
表1 系统参数

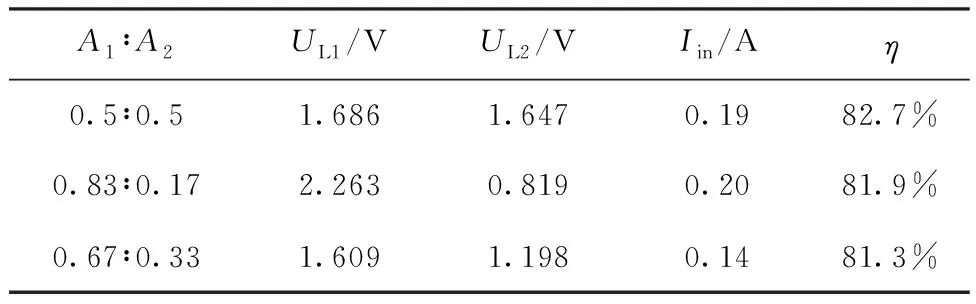
表2 实验结果

图8(a)为176.6 kHz与205.4 kHz叠加而成的交流波形,图8(b)为上述双频率叠加波形经锯齿载波调制后输出的GaN开关管导通信号波形,该导通信号是包含两个不同频率、不同幅值正弦波信息的方波信号。图9为两负载端在不同输入电压幅值比的条件下接收的直流电压。从图9中可以看出,通过调节输入频率信号电压幅值比,可以实现预期的功率分配目标。根据表2的实验结果,采用不同电压幅值比时,系统总体传输效率均维持在80%以上。系统输入电流与GaN开关管DS两端电压如图10所示。可以看出,该系统实现了逆变器GaN开关管在ZCS条件下工作,从而大幅降低了开关损耗。

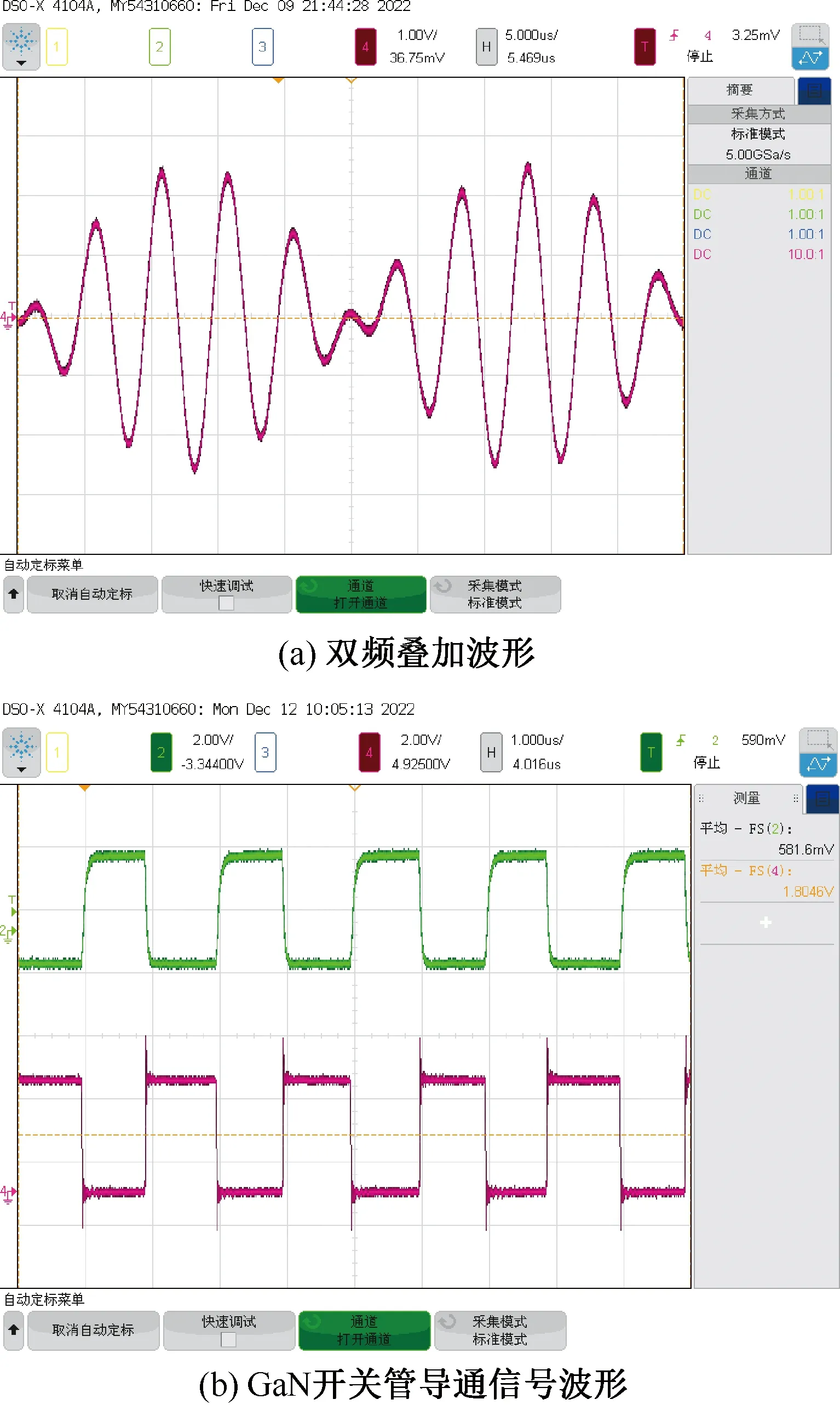
图8 双频叠加波形及GaN开关管导通信号波形

图9 接收机输出电压

根据验证的结果,将本系统与现有技术进行了比较,结果如表3。

表3 与现有技术比较

5 结 语

本文提出了一种基于LCL补偿的双频双负载MCR-WPT系统,将MFMA叠加调制方法应用于双频双负载MCR-WPT系统,该方法仅需一个逆变器即可满足多谐振频率接收机的功率传输及分配需求。文中建立了系统的数学模型,通过分析输入阻抗的频率特性,确定系统的自然谐振频率,提出基于粒子群算法的参数设计方法,可根据实际应用中的频率需求,快速准确地调节系统各参数,实现每个频率信号的独立功率传输通道。实验验证该系统可以通过改变相应谐振频率的输入电压幅值,来调节对应的输入功率,而不需要在接收侧使用额外的DC-DC模块来实现功率分配,且系统工作在ZCS状态,可大幅降低系统开关损耗。