基于不对称齿顶结构的电机振动噪声削弱研究

于国健,吴胜男

(沈阳工业大学 电气工程学院,沈阳 110870)

0 引 言

高速电主轴电机对整个工作机床的稳定与精度至关重要,低振动、低噪声的高速电主轴用永磁同步电机研究就变得更加有意义[1]。

定子齿部受径向电磁力波动进而产生振动,学者们通过改变定子齿顶结构来抑制振动。文献[2]先运用解析法推导齿顶削角的磁密表达式,之后运用有限元法对4种定子齿削角方案对比分析,确定了在定子齿四分之一处进行削角时减振降噪效果最好。同样,还有通过减小永磁同步电机定子齿厚度或者对定子齿中心进行偏心等方法来减小径向电磁力幅值,进而削弱电机振动噪声,但是这些方法也会使电磁转矩下降[3-5]。

为了解决减小径向电磁力时使得电磁转矩减小的难题,更多学者从设计之初就选择开展多目标优化算法来实现转矩增加。文献[6]对电机的定子槽口宽、齿桥根部厚度、齿冠半径以及永磁体极弧系数4个参数,对电机的转矩、电磁力进行优化。文献[7]将转子磁钢的极弧系数、磁钢厚度和定转子之间气隙径向距离作为优化参数来进行优化。

本文分析定子齿顶电磁力分布规律,并利用智能优化算法降低电机径向电磁力幅值,达到减振降噪的目的。

1 永磁同步电机有限元分析

1.1 永磁同步电机结构

本文研究的4极18槽高速永磁同步电机的截面图如图1所示。该电机的主要参数如表1所示。

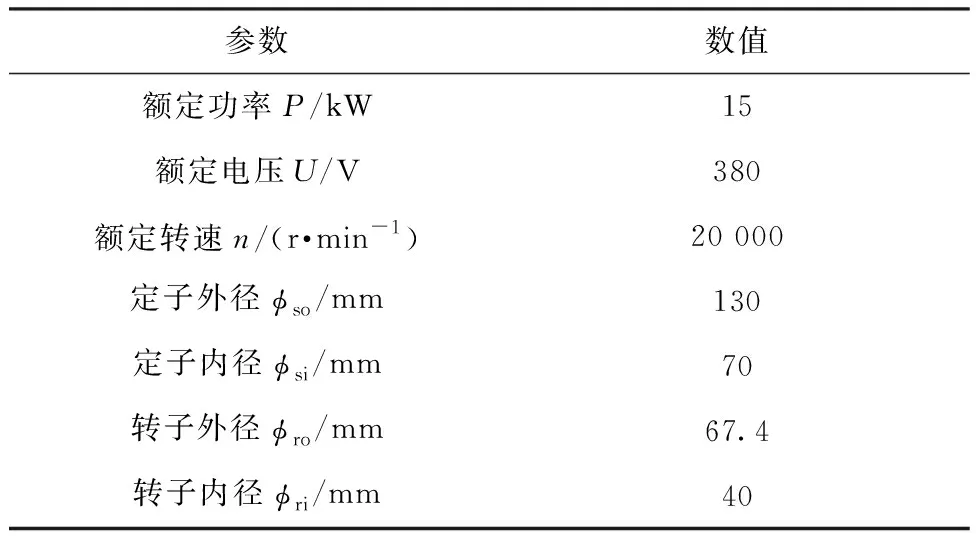
表1 电机主要结构参数

图1 电机截面图

1.2 电机径向电磁力与振动噪声的关系

在研究电机电磁振动过程中,可以将电机等效成一个机械模型,根据机械阻抗理论,电机定子铁心振动位移可以表示:

(1)

式中:Fm是径向电磁力幅值;K是定子轭刚度;m是定子轭质量;ω是角频率。振动是噪声的来源,噪声不仅与电机表面振动特性相关,同时也与周围介质的性质相关。电机表面辐射噪声声功率的表达式:

(2)

式中:Sf是定子外表面面积;ρ0是周围介质密度;σm是定子铁心声辐射系数;c是声音在介质中的传播速度。根据式(1)和式(2),径向电磁力大小直接影响电机振动水平,从而影响辐射噪声,因此从源头上降低径向电磁力幅值可以优化电机振动噪声水平[8]。

1.3 电机径向电磁力有限元仿真分析

通过麦克斯韦张量法编辑的电磁力计算结果为径向电磁力密度,后文均简称为径向电磁力。在电机气隙圆周内做圆形分析路径可以观测电机径向电磁力的空间分布,如图2所示。而对气隙内一点进行时间分析时可以得到电机径向电磁力的时域分布,如图3所示。

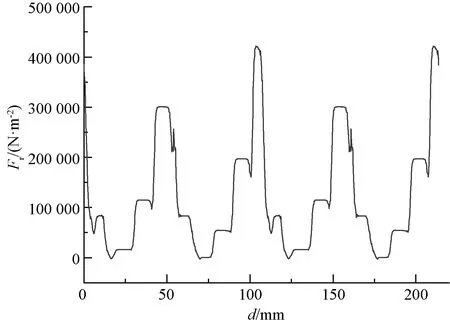
图2 径向电磁力空间分布

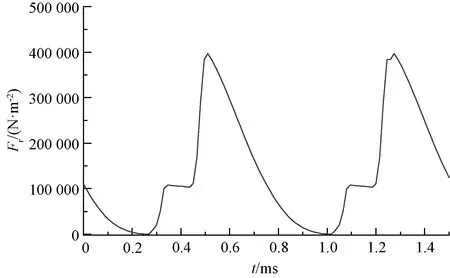
图3 径向电磁力时域分布

电机气隙中的径向电磁力具有时间、空间二维属性,因此本文利用时空分布和二维傅里叶分解来分析径向电磁力的时空特性。图4和图5给出了电机负载状态下的二维径向电磁力时空分布及谐波成分特性。

图4 电机径向电磁力时空分布

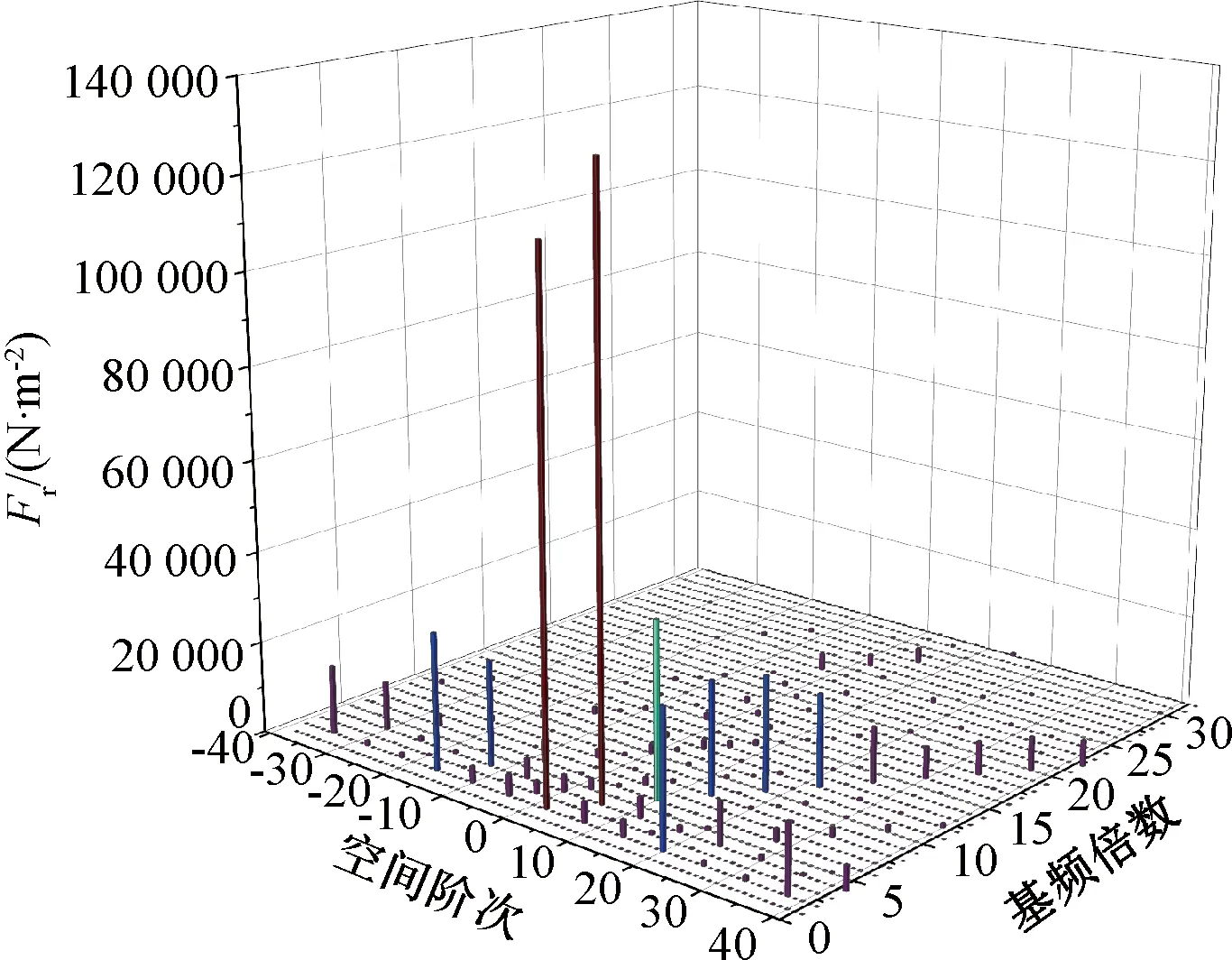
图5 电机径向电磁力谐波成分

由图5可知,径向电磁力在频域上的主要成分为基波频率的偶数倍,空间分布的主要成分为电机极对数的偶数倍,而电机的振动噪声与径向电磁力幅值成正比,与径向电磁力阶数的4次方成反比,所以针对图5中幅值较大、阶数较低的径向电磁力进行削弱,即可有效地降低电机振动噪声。

2 智能算法迭代优化

径向电磁力产生于磁场,作用于结构场,是引起电磁振动的主要因素,而由其引起的定子振动又与径向电磁力阶数4次方成反比,削弱低阶径向电磁力的幅值对削弱振动、减小噪声至关重要。而在优化过程中,电机结构参数的变化会使电机其他的电磁性能受到影响,所以也要同时考虑电机的转矩与转矩脉动性能。上文对电机径向电磁力分析时,其空间分布的波形是空间阶数的分析来源,对径向电磁力空间分布的幅值进行削弱,就会削弱低阶径向电磁力的幅值。所以本文将以空间分布的径向电磁力幅值、转矩性能作为优化目标,以定子齿槽参数为优化变量进行多目标优化,达到抑制电机振动噪声的目的。

通常来说,参数化建模定子模型之后进行数值迭代优化时,需要每一次都根据参数的变化建立新的定子模型之后再进行求解计算,计算结果准确性高,但是在模型数量较多时,计算时间比较缓慢,而田口法缩小模型计算数量的方法又不能直接选择最优方案。本文利用智能算法BP神经网络模型进行电磁力、平均转矩和转矩脉动的迭代优化。

BP神经网络可以通过样本数据的训练,实现m个输入参数到n个输出参数之间非线性关系的映射。本文通过有限元计算25组数据作为模型的训练数据及预测数据,样本数据如表2所示。数据的预测变量为电机定子内径di1、定子槽肩高h1和槽口宽度b0,响应变量为径向电磁力、平均转矩及转矩峰峰值。

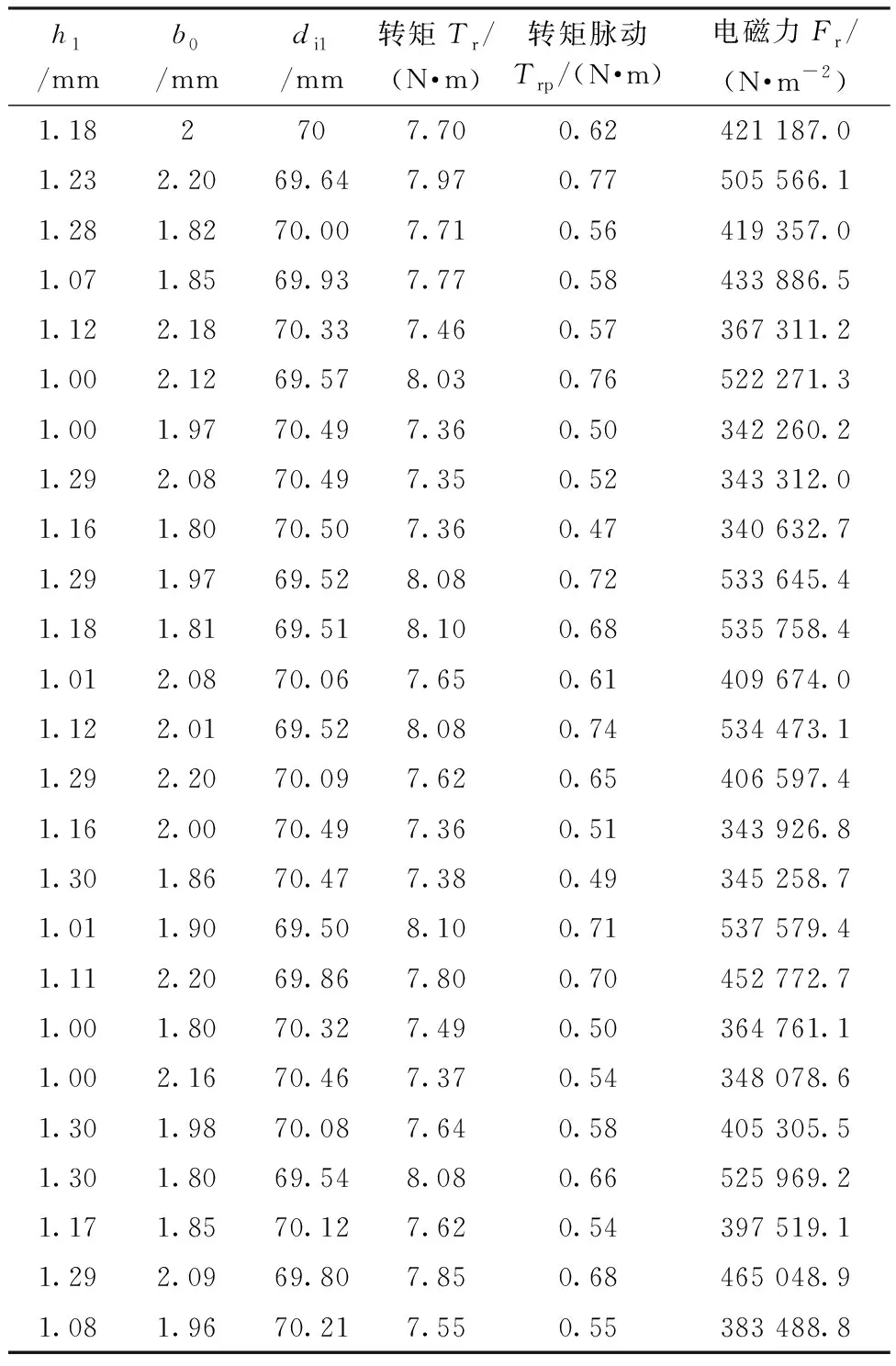
表2 BP神经网络训练和测试样本

取其中20组结果作为训练集,训练集其中15%为实验数据,以剩余5组数据为测试集,最终BP神经网络模型,其结构如图6所示,具有3个输入,3个输出,10个隐含层节点。

图6 BP神经网络预测模型

表3为训练数据和仿真数据对比。可以看出,预测具有较高的精度,之后通过训练好的BP神经网络模型代替有限元软件进行迭代计算,并利用NSGA-Ⅱ多目标遗传优化算法,得到径向电磁力幅值、转矩和转矩峰峰值的Pareto前沿,如图7所示。优化前后的定子参数如表4所示。

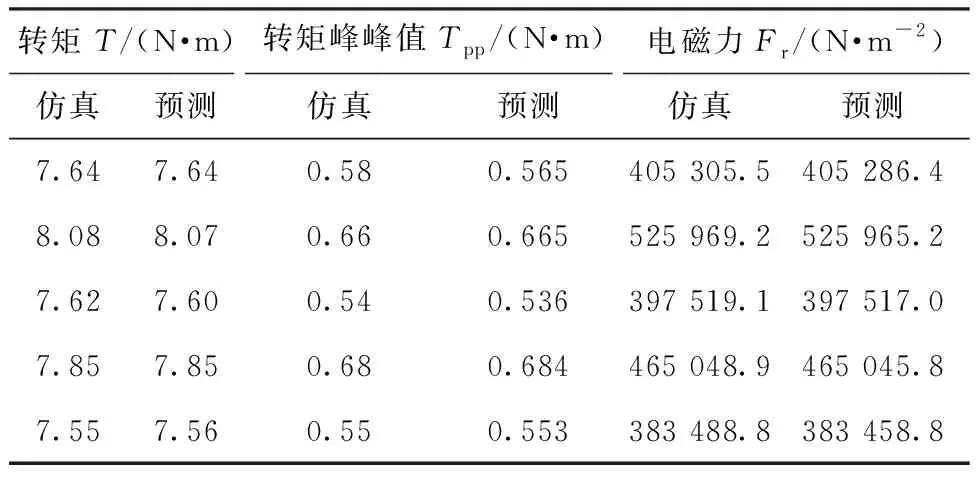
表3 预测数据与仿真数据对比

表4 优化前后定子参数

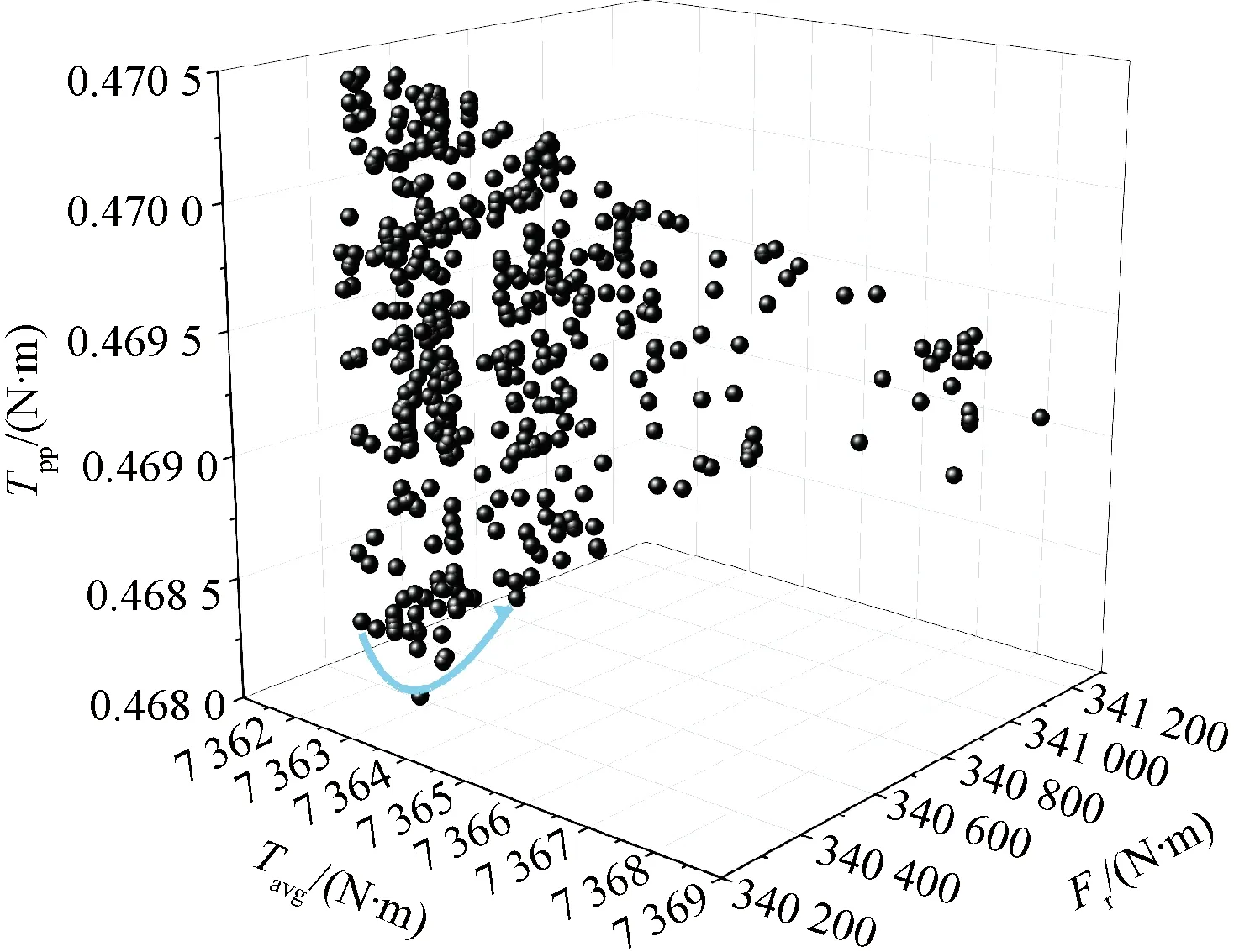
图7 Pareto前沿图

为了验证上述方案的优化效果,分别对优化前后的电机进行建模,并分析了电机性能的对比如表5所示。

表5 优化前后电机性能对比

通过表5可以发现,在对原电机进行多目标优化后,平均转矩有所下降,从优化前的7.7 N·m,下降到7.36 N·m,降低了4.4%,优化后转矩脉动由8.0%降低到了6.4%,且电磁力幅值由421 211 N·m-2降低到了350 451 N·m-2,降低了16.7%,即改变齿槽参数后,电机的径向电磁力幅值被有效削弱了。

3 减振结构设计

进一步对优化后的电机定子结构进行优化定子齿所受的径向电磁力是时空属性的,本节将根据此分布规律提出减振降噪方法。因为电机径向电磁力在电机圆周上不断旋转,呈周期性,故只分析电机一个定子齿即可。分析路径如图8所示,不同时刻下的径向电磁力空间分布规律如图9所示。

图8 定子齿顶分析路径示意图

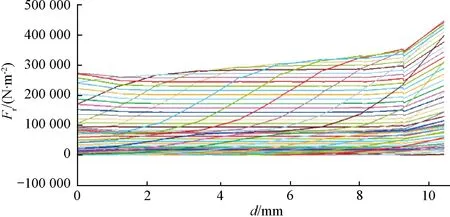
图9 不同时刻径向电磁力空间分布

图9给出了在一个定子齿下不同时刻的径向电磁力空间分布,从图10中可以看出,在电磁力稳定的时间段,一个齿顶下的大部分电磁力从左到右呈现先降低再不变再增加的趋势,且增加时的趋势更加明显,在100个时间点内,少量时间下的齿顶径向力一直呈现上升趋势,这是因为转子位置变化,导致径向电磁力由低幅值到高幅值,所以在考虑多数时间点下的径向电磁力,齿顶左右两端受到较大的径向电磁力,且左右受力也不均匀,容易弯曲变形。

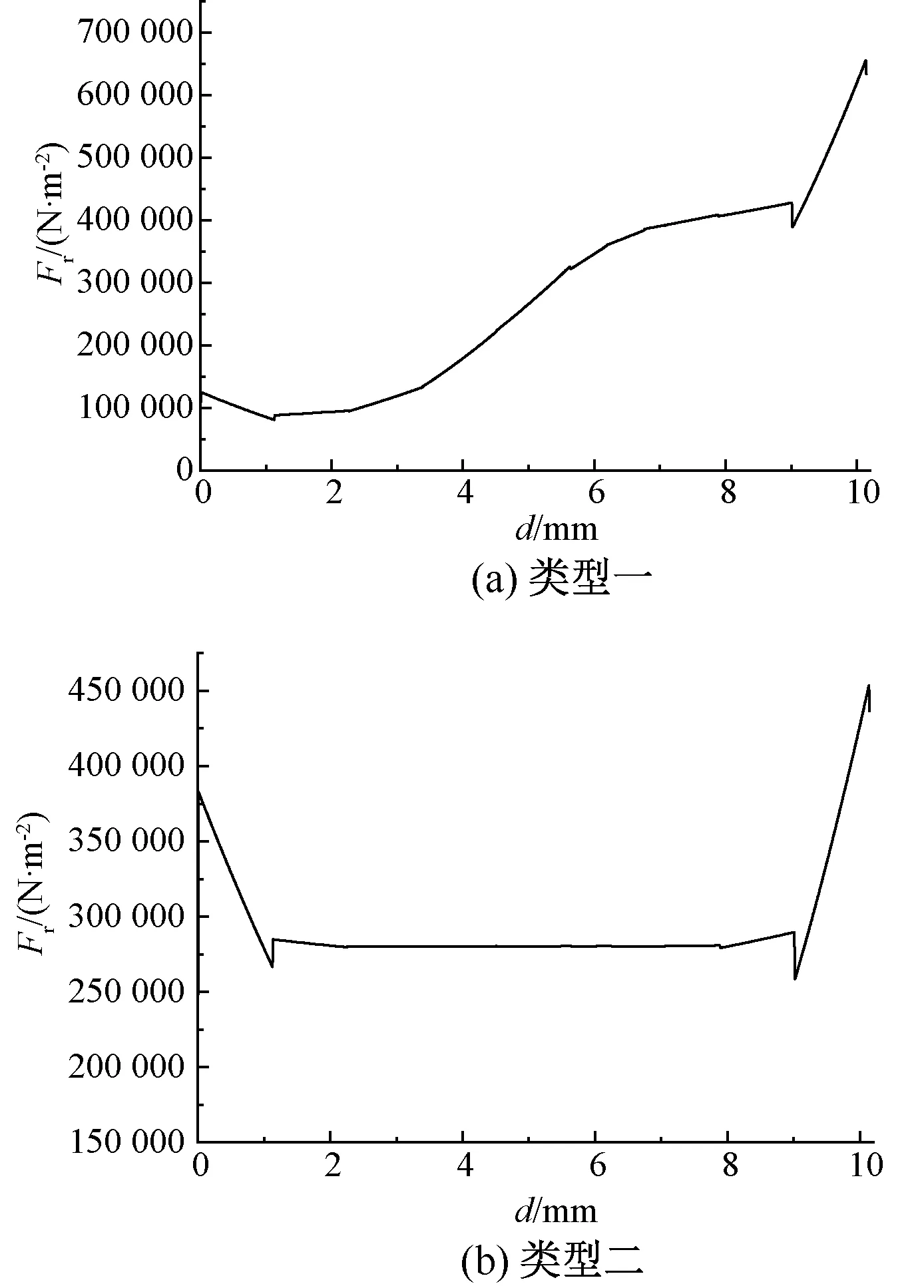
图10 两种不同分布规律

当认为类型二的径向电磁力引起振动的权重更大时,可以采用定子齿两端削角的方式改变定子齿下磁阻,有利于削弱幅值较大的径向电磁力,达到抑制电机振动的目的。具体的定子齿结构优化示意图如图11所示。

图11 不对称齿顶结构示意图

由图11看出,在齿顶下,左右两端径向电磁力幅值发生改变的占比都为11.5%,在齿顶长度为10.4 mm的情况下,即H0取1.2 mm固定不变,而在采用对称齿顶的情况下,在削角时气隙磁密和径向电磁力则会随之减小。所以H1,H2从0.1 mm到0.5 mm每0.1 mm进行削角。定子齿不同削角方案下径向电磁力幅值以及转矩对比如表6所示。

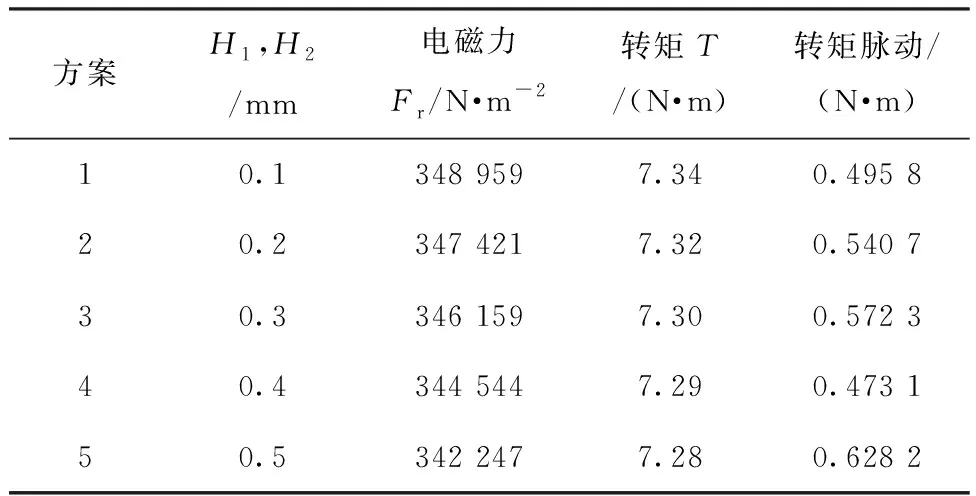
表6 对称削角方案对比

当采用不对称齿削角时,即H1,H2不相等时不同方案电磁力幅值、转矩对比如表7所示。

表7 不对称削角方案对比

由图12和图13可以发现,当对称齿顶结构的方案与不对称齿顶结构的方案H1相同时,两种结构具有相近的转矩,而不对称结构H2的增大则进一步减小了电磁力幅值。所以最终采用不对称齿顶结构的方案5,即H1=0.2 mm,H2=0.5 mm,此结构的优化结果与原电机径向电磁力对比如图14所示。可以看出,在算法优化及采用不对称齿顶结构后,电机径向电磁力各阶幅值有了明显的下降。

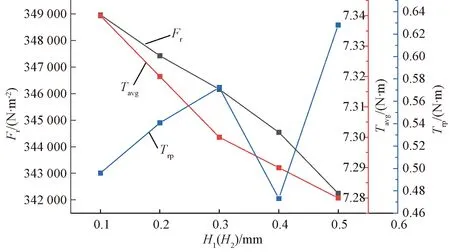
图12 对称削角方案优化目标的变化

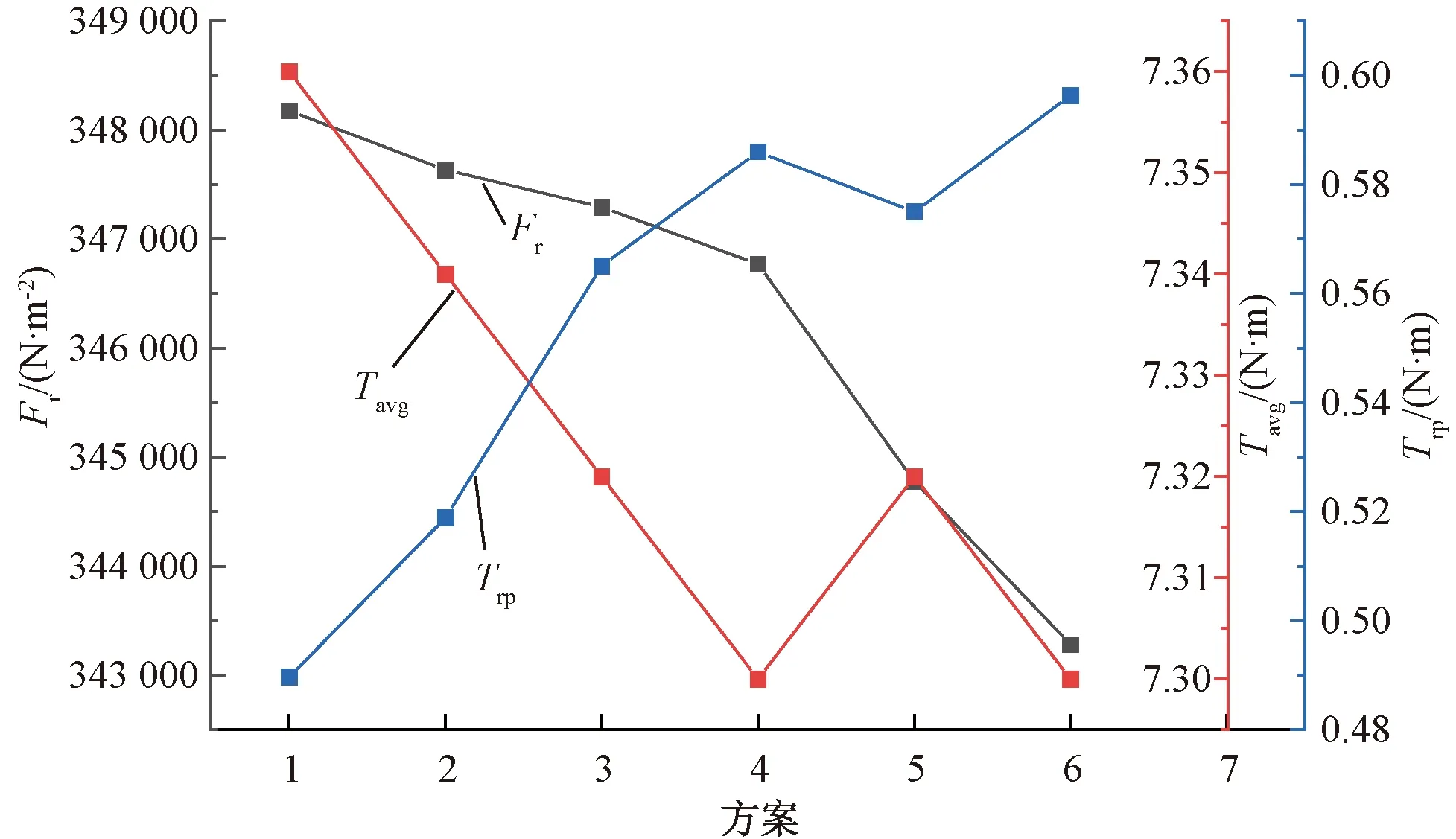
图13 不对称削角方案优化目标的变化

图14 径向电磁力空间分布对比及谐波对比

4 振动噪声分析

本节基于Workbench有限元仿真平台进行电机振动与噪声仿真,验证上文提出的算法优化与结构优化相结合的效果。二维有限元仿真的电磁力结果导入进谐响应模块是在三维电机结构的定子齿面以集中力的形式显示,同时结果的导入也有转矩的结果,定子齿面的转矩分布和电磁力分布如图15和图16所示。

图15 转矩分布示意图

图16 电磁力分布示意图

振动分析的过程是将电机机壳外表面作为电机振动加速度的分布部分,在设置中使谐响应分析模块中频率的设置与电磁分析中的时间相对应,同时对电机机壳的螺孔施加固定约束。通过仿真可以得到电机在20 000 r/min的振动加速度结果,将优化前后电机振动加速度结果进行对比如图17所示。

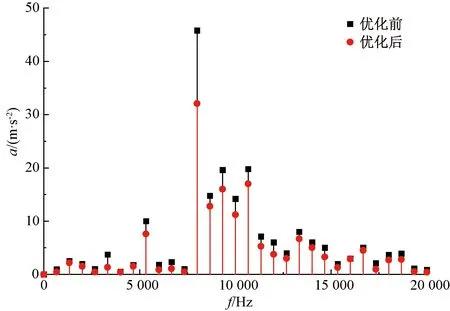
图17 优化前后的电机振动加速度对比

由图17可以看出,通过优化定子结构并结合不对称齿顶结构可以有效地降低电机的振动加速度,最大值降低了10%。

将优化后的电机进行相应的噪声仿真,得到距电机0.4 m一点的优化前后声压级结果,如图18所示。

从图17和图18可以发现,本文采用多目标优化与不对称削角结构相结合,削弱了定子齿顶下幅值较大的径向电磁力,达到了抑制电机振动噪声目的。电机经过优化后振动加速度与噪声声压级有下降,振动加速度最大值降低10%,噪声声压级值由87 dB下降到83.5dB,降幅为4.2%。

为了验证上述的分析结果,通过实验测试了电机20 000 r/min时的振动特性,实验平台如图19所示。

电磁振动有限元仿真谐响应结果与实验结果对比如图20所示。

图20 电机振动加速度仿真与实验结果对比

由图20可以发现,电机振动加速度的仿真结果与实验结果存在一定偏差,但是仿真结果可以反映出电磁振动加速度随频率的变化趋势。仿真模型用于评估电磁振动,而忽略了实际定子复杂几何结构的影响。此外,实验结果不仅包括电磁振动,还包括机械振动。综上所述,实验结果与模拟结果吻合较好,可以证明仿真计算的有效性。

5 结 语

本文采用智能迭代算法可以有效地加大计算的样本量并减少运算时间,而采用不对称齿顶的结构可以有效地降低电机的径向电磁力幅值,从而减小了电机的径向电磁力谐波分量,降低了电机的振动与噪声,为削弱电机电磁振动的分析提供了参考。