对洁净空调箱送风量控制策略的讨论及测试
文/崔吉想 张雪娇 李春雷 尤锦 周燚 欧阳健
在药品生产企业中尘埃粒子是通过洁净空调箱来去除,洁净区域内的温湿度也是由洁净空调箱来调节的——为了维持洁净区域内的换气次数和压差,洁净空调箱需要输出恒定的送风量。然而,系统中过滤器的脏堵和外界湿度的变化,都会对运行状态产生干扰。本文针对目前制药企业实际使用的几种洁净空调箱送风量的控制方法展开了讨论。
1.现有空调箱送风量控制方法
笔者对现有的几种控制方法进行了随机调研,它们各自的占比情况件如图1 所示。从图1 中可以看到尚没有占据绝对优势的控制方法。本文将分享一下各种控制方法的原理,并用数据来说明选择哪种方法更为合理,评判的基准在于:一个优秀的控制方法,既要控制有效又要运行节能。

图1 空调箱送风量控制的潜在方法及占比
1.1 采用洁净空调箱出口的静压来控制
采用空调箱出口的静压关联风机变频器,这种方法在调研结果中的占比较高。空调箱自控程序的编写人员多为非暖通专业出身,对静压、动压与送风量的逻辑关系理解不深,程序逻辑仅是将静压与风机变频器正关联在一起;关联的逻辑是如果出口的静压大就降频,反之,出口的静压小就升频。这样会导致洁净区域的高效过滤器堵塞越严重,控制系统输出的执行反而越降频,满足不了区域内换气次数要求的问题发生。不仅如此,这种设计也可能会导致另外一种事故:如果空调箱负压端的门不小心被打开,造成其出风口风量增加,动压加大;在全压(全压=静压+动压)不变的情况下,随着动压的增加,静压则会降低,控制系统输出就会升频,最终形成恶性循环将末端高效过滤器吹破。
如果学习过化工原理课程就会知道,静压是发散、没有方向性的,因此从自控角度看,实际上静压与风速是没有逻辑关联的。为了避免上述的恶性情况发生,一般会在末端高效过滤器前安装一个定风量阀,这样便能始终将送风量维持一个较高的水平。这种方法会无谓地消耗电动机的能量,也不能够进行有效的控制,因此笔者并不推荐。
1.2 采用洁净空调箱出口的风速来控制
由于风速乘截面积便等于送风量,因此采用出口风速来控制送风量就显得可靠易行,事实上在调研结果中采用该方法的占比也是最高的。但在实际运用中,空调箱出口安装的风速仪会受到前后气流扰动的影响。如果想要风速仪的测量数据更为准确,就需要在其前后都留有足够的直段,这在实际施工中存在一定的难度。
不过风速的波动变化相对较小,不会影响对送风量的控制,而且风速与送风量之间存在正关联的关系,在实际控制中风速也仅当刻度来使用。因此可以在风速仪界面上找到一个比较合适的位置,用来关联风机的变频器从而达到控制送风量的目的。
1.3 采用洁净空调箱出口的动压来控制
这种方法的原理在于用毕托管来测量出口的动压,在获得空气动压值后,即可利用如下的公式计算出空气的流速:
毕托管在实际应用中与风速仪同样,也会受到前后气流扰动的影响,但是动压数值的波动变化范围较小,而且毕托管的抗干扰能力比风速仪要好,所测得的数据比风速仪更接近实际的数值,对所控制送风量的变化影响更小,适合做联动控制。但在实际调研结果中,该方法使用的占比却是最小的。
1.4 采用风机喉部的静压差来控制
现在洁净空调箱已普遍采用无蜗壳风机,不再使用之前皮带带动的蜗壳风机。无蜗壳风机是一种离心风机,不需要蜗壳,因此可以减少能量损失和噪声,提高风机的效率。它通常采用直接驱动方式,即电动机直接连接到风机叶轮上,没有中间的传动装置。由于没有蜗壳,无蜗壳风机的体积和重量较小,可以更方便地安装和维护。
无蜗壳风机有一个喉嘴特性参数K。K 对于同一型号的无蜗壳风机来说是一个常数,K 乘以风机喉部与前箱体的静压差△pw的平方根(如图2 所示)即得送风量。用它来关联变频器控制送风量,可能不仅投入少且效果最好。由于该方法的控制非常简单,所以笔者所在团队尝试对其进行了一次测试(测试过程及结果可见文章第2 部分)。在无蜗壳风机的喉部有一个静压的检测口,然后再在前箱体上设置一个静压的取样点。这两个静压之差就是△pw值,而喉嘴特性参数K 是可以从风机的参数表上查得的(本次测试中的K=154)。
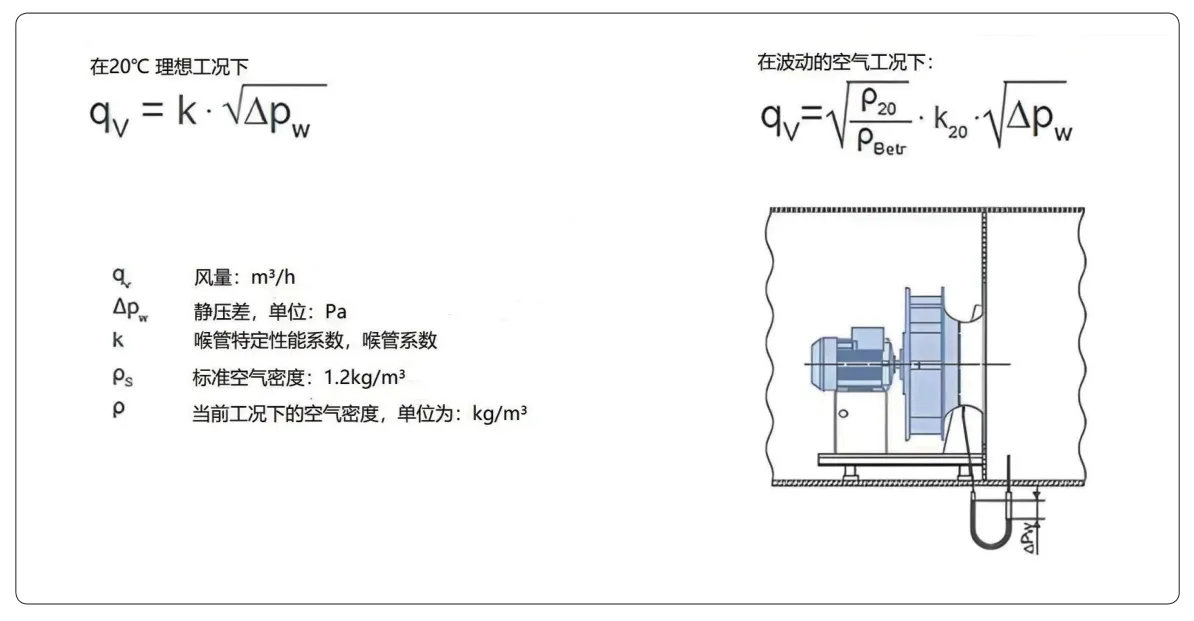
图2 风机喉部的静压差控制示意图
2.用风机喉部静压差控制送风量的测试
2.1 测试过程
为了确认采用风机喉部的静压差来控制送风量在实际运行中的可靠性,笔者团队在博纳环境设备(太仓)有限公司的支持下,现场将该方法得到的数据与按EN 1886 要求用毕托管测风量所得的数据进行了比对。我们现场随机选择了一台正在进行FAT(工厂验收测试)的空调箱(配置了施乐百的ER40C 风机),并且预定了大致在85%、90%、95%、100%和105%的设计送风量的情况下来进行比对,实验过程中测得的数据汇总于表1 中。
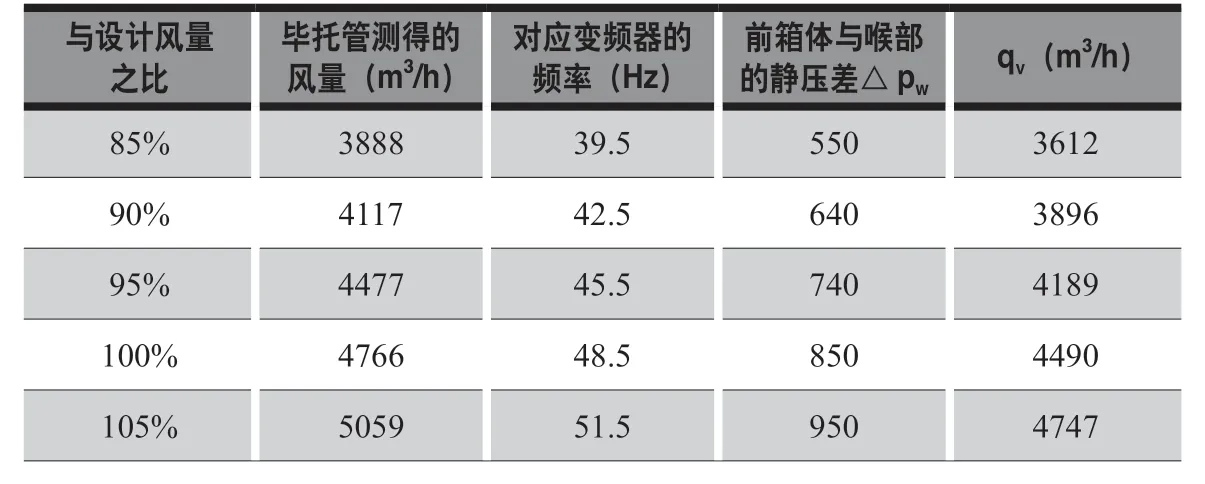
表1 测试数据和计算数据汇总表
表格中数据的计算公式为:
式中:△pw——风机前箱体对风机喉部的压差;
K——喷嘴的压力系数,对于ER40C 风机来说,从图3 可查得为154;
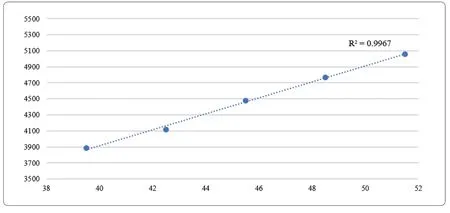
图3 毕托管测得风量与频率的关系
qv——用喉压计算所得的送风量(m3/h)。
首先根据毕托管测得的风量与风机变频器的频率作图,可以得到如图3 所示的散点图,然后再将其拟合为一条直线趋势线。从图3 中拟合的直线来看,送风量与风机频率的关系是呈线性的,R2为0.9967,显示其线性相关性已非常好。
然后根据喉部压差计算得到的风量与风机变频器的频率来作图,可以得到如图4 所示的散点图,它也可拟合为一条直线趋势线。从图4 中拟合的直线来看,送风量与风机频率的关系也呈线性,R2为0.9994,显示其线性相关性也非常好,而且似乎比用毕托管测得的相关性还要更优秀一点。

图4 用△pw 计算所得风量与频率的关系
为了更直观地分析两组数据的差异,我们将两组数据整合在一张图中(如图5 所示),便于对两组数据进行对比。从图5 中可以清晰地看到,用△pw计算的数据与毕托管测量的数据似乎仅相差一个截距常数。这代表它们两者之间存在一个系统偏差,而用△pw计算得到的数据其线性关联更好,并且绘制的直线通过原点,这说明似乎用喉部压差计算得到的结果更为精准。
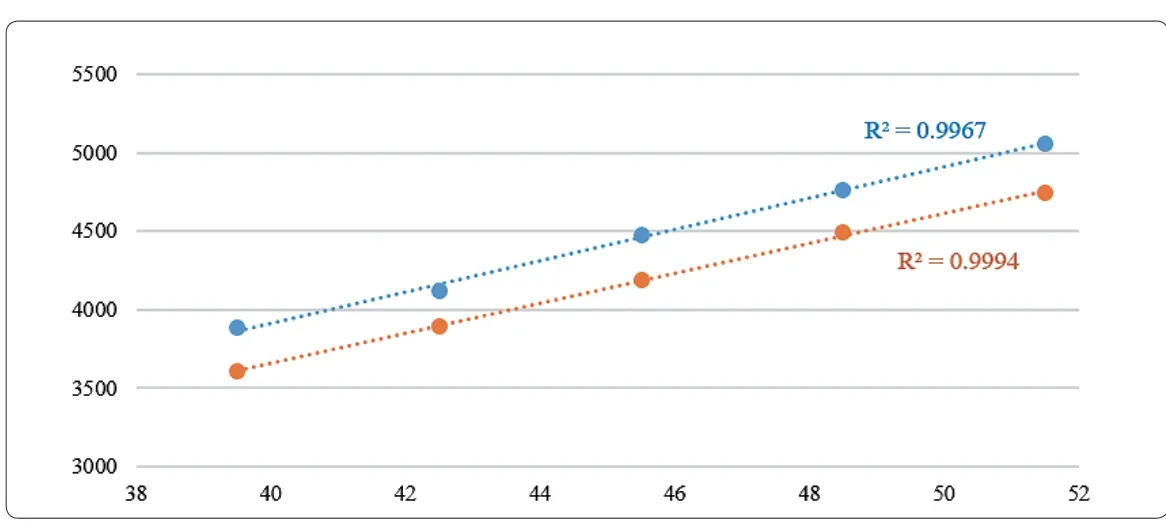
图5 毕托管监测数据和△pw 计算的数据整合图
2.2 测试结论
如果在喉部压差计算公式上加一个常数300,将上述的公式(2)变为下面的公式(3),可以使得两条曲线基本吻合(如图6 所示)。
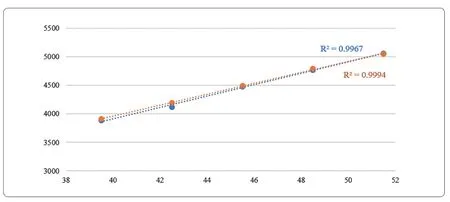
图6 修正公式作图
但考虑到用△pw计算得到的数据图像是通过原点,而用EN 1886 中的方法测量时,数据间的差别较大,所以笔者不认为这样手动加常数去拟合是合理的,仍然推荐用公式(2)的算式来关联送风量和风机频率。

