基于CE-QPSO算法的联合火力打击方案智能优化方法

王赞程,贺筱媛

(国防大学,北京 100091)

联合火力打击是联合作战的重要环节,如何科学、精准、高效地优化联合火力打击方案,是联合作战筹划中的重难点问题之一[1]。联合火力打击方案优化问题的核心在于合理组织火力打击力量、有效进行武器—目标分配[2],该问题在军事运筹领域属于火力分配(Weapon-Target Assignment,WTA)问题,是典型的NP完全问题[3-4]。

随着信息技术与人工智能的不断发展,智能优化算法逐步取代传统的手工作业方法,成为解决火力分配问题的有效方法。目前,该问题常用的智能方法包括:果蝇算法、遗传算法、蛙跳算法、蚁群算法、布谷鸟算法、模拟退火算法等[5-10],上述算法各具优势,但也都存在着如参数调节复杂困难,运算效率低下,易陷入局部最优等问题。相比之下,粒子群算法因其运算规模小,收敛速度快等优点,在火力分配问题中广泛应用,效果显著[11-13]。

由于联合火力打击方案优化问题涉及目标数量、武器弹药类型繁多,问题规模和复杂度远高于以单一兵种为主的火力分配问题[14],而标准粒子群算法也存在着易陷入局部最优,对高维复杂模型寻优精度差等问题。因此,本文在构建联合火力分配模型、设计方案评价指标的基础上,提出了交叉熵-量子粒子群优化(CE-QPSO)算法,结合交叉熵算法良好的全局寻优能力和量子粒子群优化算法高效运行的特点,提升对高维复杂函数的优化效果与优化效率。通过仿真实验,验证了CE-QPSO算法解决火力打击方案优化问题的有效性。

1 问题描述与模型构建

1.1 联合火力打击方案优化问题

联合火力打击方案优化问题,即在限定的目标毁伤要求、武器种类、弹药量等条件下,综合考虑目标价值、毁伤效能和弹量消耗等影响因素,重构现有联合火力打击方案中武器弹药与目标间的匹配关系,实现毁伤效果的优化和打击成本的降低。

在某次联合火力打击行动中,有n个需要打击的目标,表示为T={T1,T2,…,Tn};有m类武器,表示为W={W1,W2,…,Wm},其中,第i类武器的可用弹药量为ci。定义二值决策变量xij,xij=1表示选用第i类武器打击第j个目标,否则xij=0,则可以将联合火力打击方案形式化描述为决策变量矩阵X=(xij)m×n。

1.2 联合火力分配模型

从影响因素、约束条件、优化目标三方面,建立联合火力分配模型。

1)影响因素。联合火力打击方案的优化,受到目标价值、毁伤概率、耗弹量等多种因素影响。定义第j个目标的打击价值为vj;第i类武器打击第j个目标的毁伤概率和耗弹量分别为pij、qij。

2)约束条件。联合火力打击方案的优化,受到目标毁伤要求、弹药量等条件的约束。首先,应保证每个目标均被打击,即

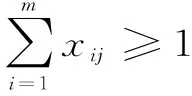
(1)

此外,每类武器的耗弹量不能超过其可用弹药量,即

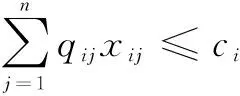
(2)

3)优化目标。从毁伤效果和打击成本两方面,考虑联合火力打击方案的优化目标,定义目标毁伤率指标D和弹药消耗率指标E:

(3)

(4)

为实现联合火力打击方案的综合评价,将上述指标通过线性加权的方法转化为单目标评价函数:

S(X)=αD(X)+β(1-E(X))

(5)

其中,权重参数α、β大于0,且α+β=1。

综上,建立联合火力分配模型:

(6)

2 联合火力打击方案智能优化方法

联合火力打击方案智能优化方法,可分为数据获取、方案转录、智能优化三个步骤,其基本流程如图1所示。

图1 联合火力打击方案智能优化方法流程图Fig.1 Intelligent optimization method flow chart of joint firepower strike plan

1)数据获取部分。依托战场实时态势数据,生成目标价值表;通过大样本作战实验,对各类武器弹药的毁伤效能进行预测和修正,生成武器-目标一一对应的毁伤概率矩阵、耗弹量矩阵。最后通过清洗、转换操作对上述数据进行格式上的统一和规范。

2)方案转录部分。基于已经构建完成的联合火力分配模型,对现有联合火力打击方案进行形式化描述和格式化编码,将自然语言转化为程序语言。

3)智能优化部分。基于设计好的方案评价指标和评价函数,对现有方案进行综合评估,并以此为优化目标,采用智能优化算法迭代运算,将优化结果转化为格式化方案输出。

3 CE-QPSO算法

联合火力打击方案智能优化的关键在于采用合适的智能算法,进行联合火力打击方案优化问题的求解。本文提出CE-QPSO算法,结合交叉熵算法的离散概率估计和量子粒子群优化算法的随机更新策略,实现优化效果和优化效率的提升。

3.1 交叉熵算法

交叉熵(CE)算法是一种可靠性分析与随机优化设计的统一方法,其本质是将优化问题转化为概率估计问题[16]。

一般情况下,假设S是有限状态集χ上的实值函数,CE算法将寻找该函数最大值的优化问题转化为概率估计问题:

(7)

l(γ)=Pβ(S(X)≥γ)=EβI{S(X)≥γ}

(8)

其中,式(7)表示原始的优化问题,即在统计样本集X中,找到函数S的最大值γ*,以及能使S取到γ*的状态X*。式(8)表示转化后的估计问题,γ为接近γ*的值,在参数β下,S(X)取最大的概率,即为示性函数I{S(X)≥γ}对应的期望。

为求解该问题,需要对l(γ)进行无偏估计:

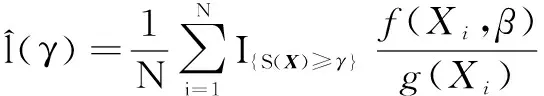
(9)

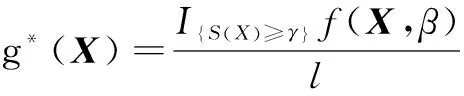
(10)

(11)

合并式(10)、(11),得到如下最大值优化问题:

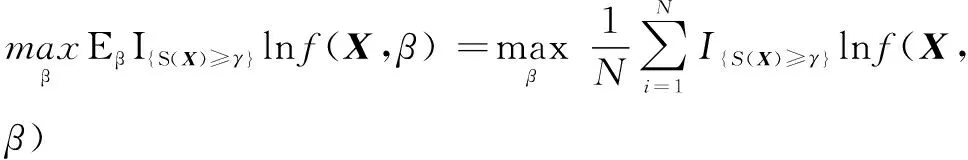
(12)

CE算法构造阈值序列{γk,k≥0},用以不断逼近γ*;同时构造参数序列{βk,k≥0},用以表征g*(X)中的参数。在每一次迭代中,根据概率密度函数,随机生成N个样本,并依据目标函数值,选取前θN个优秀样本,进行γk和βk的更新。经过T次迭代求解之后,所求得的γT接近最大值γ*[17]。

3.2 量子粒子群优化算法

量子粒子群优化(QPSO)算法基于量子力学,对经典粒子群算法进行改进[15]。QPSO算法认为,粒子遵循量子的不确定性原理,通过随机产生多个概率,利用蒙特卡洛思想进行观测,得到更新后的粒子位置。QPSO算法引入平均最优位置(mbest),并在此其基础上进行粒子位置的更新:

(13)

Pi=Φpbesti+(1-Φ)gbest

(14)

(15)

其中,pbesti表示第i个粒子的个体最优位置,gbest表示全局最优位置,xi表示第i个粒子的位置,Φ和u为(0,1)上的均匀分布数值,取正负的概率各为0.5,只有一个待调节参数η,一般不大于1。

3.3 CE-QPSO算法描述

本文提出的CE-QPSO算法,首先以CE算法构建离散概率分布函数,随机生成QPSO算法的初始粒子群;而后通过QPSO算法的量子随机游走和迭代优化,产生用以更新离散概率分布函数的优秀样本,并不断重复上述过程,算法整体流程图如图2所示。

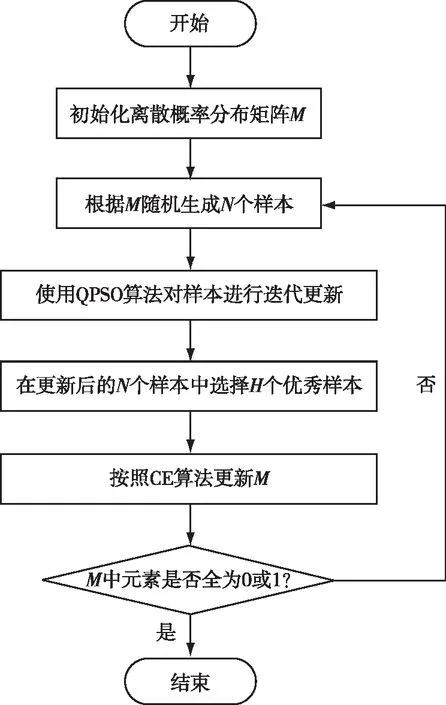
图2 CE-QPSO算法流程图Fig.2 CE-QPSO algorithm flow chart

为了优化本文构建的联合火力分配模型,将模型中的决策变量矩阵X=(xij)m×n转化为离散概率分布矩阵M=(mij)m×n。mij不再是0-1二值变量,而表示选用第i类武器打击第j个目标的概率。显然,当所有mij的值均为0或1时,M还原为X,即可确定最终的联合火力打击方案。由于毁伤效果是选用不同武器的最优先考量因素,根据毁伤概率pij对M进行初始化:

(16)

根据矩阵M,可得概率分布函数f(X,M):

(17)

(18)

根据式(15)、(17)、(18),可得到如下凸优化问题及其拉格朗日函数:

(19)

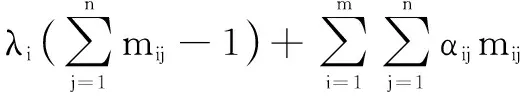
(20)

根据Karush-Kuhn-Tucker(KKT)条件,可推导得到离散概率分布矩阵M的更新公式:

(21)

因此,CE-QPSO算法步骤如下:

1)根据毁伤概率pij对离散概率分布矩阵M进行初始化;

2)根据M随机生成X1,X2,…,XN共N个样本,将其作为QPSO算法的初始粒子;

3)按照QPSO算法的粒子位置更新公式,对N个粒子进行多轮迭代更新;

4)计算更新后N个粒子的评价函数S,根据S值将粒子进行降序排序,取前H=θN个粒子作为优秀样本;

5)根据式(21),用H个优秀样本更新离散概率分布矩阵M;

6)重复步骤1)—步骤5),直至M中的元素全部变为0或1,或者达到了设定的迭代次数。此时,可认为最优秀的样本即为优化后的联合火力打击方案。

4 仿真实验分析

实验以某次联合火力打击行动为背景,计划使用25类武器弹药对191个目标进行打击。各目标价值、各类武器对各类目标的典型耗弹量和毁伤概率已通过态势数据分析和作战实验得到。初始方案由参谋人员根据上述数据,手工作业得到,并转录为计算机可识别的编码格式。

仿真实验计算机配置为Intel酷睿八核处理器i5-8300H 2.30GHz,16 G内存,Window10×6操作系统,Pycharm(Python3.7)编程平台。

4.1 参数设置

模型参数主要包括评价函数中的权重参数α和β,依据指挥员对毁伤效果和打击成本的权衡,设计α=0.7,β=0.3。

算法参数通过以下实验确定:在一定的取值范围内,每次调整一个参数的值,并通过CE-QPSO算法多轮迭代得到的最优评价函数值为参考条件,确定参数的最佳取值,如此反复,直至所有参数均设置完毕。参数的取值范围和最终确定值如表1所示。

表1 参数设置Tab. 1 Parameter setting

4.2 实验结果分析

为了验证CE-QPSO算法对联合火力打击方案的优化效果,本文采用标准CE算法、标准QPSO算法作为对比算法。优化前后方案的各项指标和综合评分数据如表2所示,其中,综合评分值和目标毁伤率指标数值越大,弹药消耗率指标数值越小,表示方案优化效果越好。

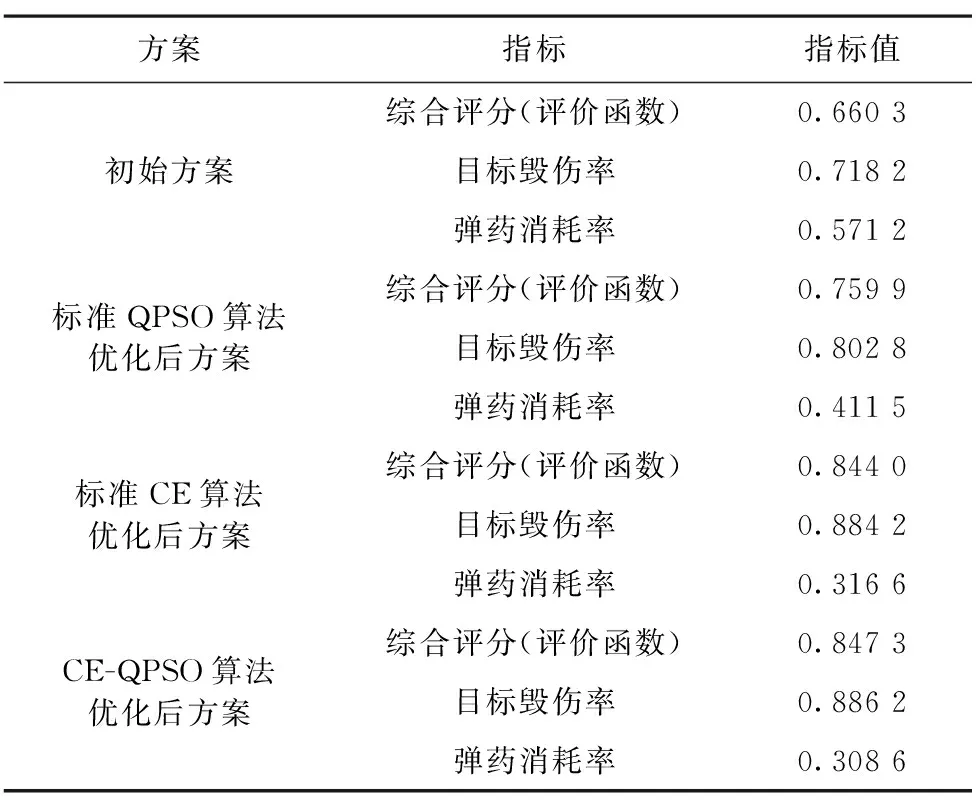
表2 实验数据Tab.2 Experimental data

为了直观体现初始方案与各算法优化后方案的优劣差别,根据表2数据,绘制优化前后联合火力打击方案的指标柱状图,如图3所示。

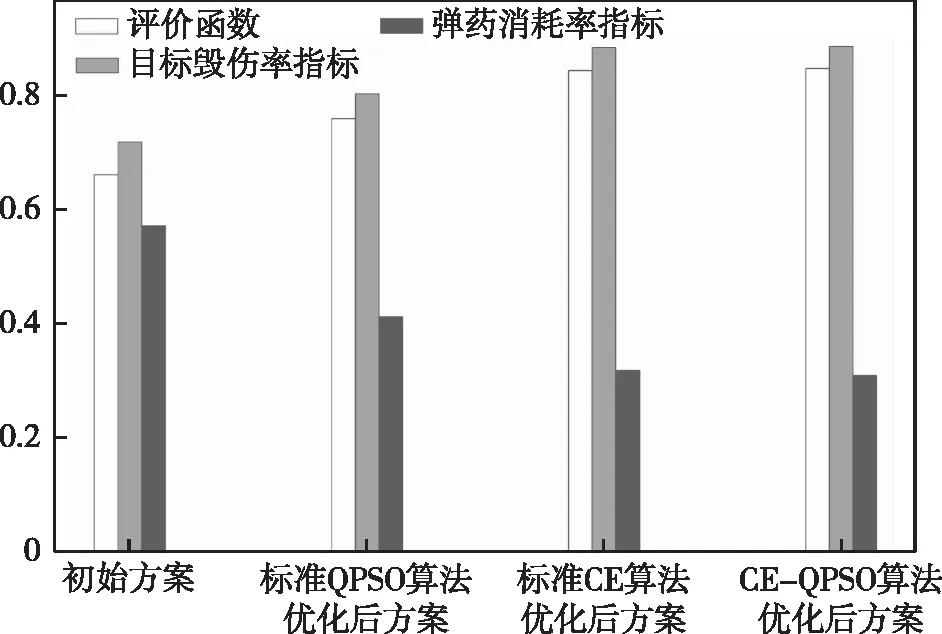
图3 方案优化前后的指标柱状图Fig.3 Index histogram before and after scheme optimization

根据表2与图3可知,三种智能算法均能实现对联合火力打击方案各项指标的有效优化。其中,CE-QPSO算法优化后方案的各项指标,均明显优于标准QPSO算法的优化结果,与标准CE算法的优化结果基本持平。证明引入CE算法,能够改善QPSO算法易陷入局部最优的缺陷,提升算法对于高维复杂模型的全局寻优能力和优化效果。

图4和图5分别给出了三种算法优化过程中,评价函数值的收敛情况,以及算法迭代运算的时间消耗。

图4 评价函数值迭代曲线Fig.4 Evaluation function value iteration curve

图5 三种算法的时间消耗Fig.5 Time consumption of three algorithms

根据图4与图5可知,尽管从优化效果上看,CE-QPSO算法与标准CE算法相比没有大的提升,但CE-QPSO算法的收敛速度和时间消耗均远胜于标准CE算法。证明利用QPSO算法得到用于更新CE算法参数的优秀样本,能够加快收敛速度,提升优化效率。

实验结果表明,综合考虑优化效果和优化效率,CE-QPSO算法的表现明显优于标准CE算法和标准QPSO算法,能够有效应用于联合火力打击方案的高效优化。

5 结束语

本文研究了联合火力打击方案优化问题,综合考虑目标价值、毁伤效果和打击成本,建立了联合火力分配模型,设计了联合火力打击方案评价指标。在此基础上,提出了CE-QPSO算法,重构了CE算法更新概率分布函数的方式和QPSO算法随机产生初始粒子的方式,充分结合两种算法各自优势,有效提升了算法针对高维复杂模型的运行效率和全局寻优能力。通过仿真实验,验证了该算法对于提升联合火力打击方案优化效果和优化效率的有效性。