海域岛礁物资补给任务智能规划*

余昌仁,乔 涵,韩梦瑶,张国杰

(陆军勤务学院,重庆 401331)

岛礁是维护我国海洋权益的前哨,是我国领土不可分割的组成部分,派驻人员守卫岛礁对保障我国领土完整具有重要的意义。远海海域诸岛礁距离大陆较远,位置相对分散[1],岛上物资匮乏,为维持驻岛人员生存生活需要,需定期由陆上保障中心派出补给船对岛礁进行补给,制定科学的物资保障方案,提高保障的效益[2]。

岛礁物资补给有特定的保障目标和影响因素,主要解决物资补给任务规划问题。岛礁物资补给任务规划问题指在满足自然停泊环境、保障时间、运输工具装载量限制等条件下,使得保障目标达到最优,保障目标包括运输工具燃油经济性、物资储存成本等,所以其本质是一个车辆路径规划(Vehicle Routing Problem, VRP)[3]问题,这类问题有精确算法与启发式算法等[4]。精确算法主要运用线性规划、整数规划、非线性规划等严格的数学方法求解,比较适合特定的问题,而启发式算法适合解决一些不规则优化问题。VRP问题常有容量约束或时间窗限制[5-6],也可能两者兼而有之,这类问题是NP(Non-deterministic polynominal,多项式复杂程度的非确定性)[7-8]难问题。智能算法作为启发式算法的一种,适合解决大规模的组合优化问题,能在解空间内高效率地寻找出极优解,典型的组合优化问题有旅行商问题(Traveling Salesman Problem, TSP)[9]、调度问题、0-1背包问题、装箱问题等。优化目标是在可行解域内找到近似解来代替最优解,减少求解需要付出的代价。智能算法包括但不限于模拟退火、蚁群算法、遗传算法、禁忌搜索算法等。

1 岛礁物资补给任务规划问题建模

1.1 模型考虑的因素

岛礁物资补给由后勤补给中心运用各型补给舰船对海域岛礁实施运输补给。考虑补给时间、补给需求和补给效益,运输投送方案最优化受自然条件、经济成本和运输工具等多种因素影响。

1)自然地理条件。岛礁附近海底地貌、岸滩底质各不相同,靠泊条件各异,对于靠泊港口大的岛礁,补给舰可直接补给,对于靠泊港口小的岛礁,补给舰须在距岛礁附近某处锚泊,通过配套小型补给艇进行转运实现间接补给,或采用某岛礁上的拖船完成物资倒运。

2)运输工具。可运用不同型号的大型补给舰,从特定的补给中心出发,补充一定数量的岛礁后再返回该补给中心。一条运输路线上仅有一艘大型补给舰。补给舰配备若干小型补给艇,拖船也可以用于短距离的物资转运。

3)运输成本。某海域领域广阔,岛礁位置相对分散,岛礁间距较远,距离是影响保障成本的主要因素。各型补给舰各有不同的燃油经济成本。规划不同的保障路径将产生不同的运输成本。拖船与小艇产生的短距离运输成本可忽略不计。

4)运输与装卸时间。各型补给舰航行速度已知,假设补给舰装有固体、液体两类物资,固体、液体的装卸也有不同的速度。各种运输工具(补给舰、小型补给艇、拖船)所载燃油能满足其去各岛补给的需要,即不考虑燃油耗尽需返回的问题。补给舰(艇)卸载固体物资和液体可同时进行,互不影响,回程时,需要从岛礁装载固体回收物。

5)储存成本。某海域岛礁大多属于热带、亚热带海洋性气候,具有高温、高湿、高盐的突出特点,各类物资易腐烂变质,长期存储需采取低温冷藏保鲜。物资储存成本也是物资补给应考虑的重要方面。固体、液体储存成本以储存天数和吨位数平均计算,单位为元/吨·天。

6)补给要求。各岛礁存储空间有限,固体、液体物资均有最大储存量,各岛礁补给之前有一定的剩余储备量,固体、液体消耗速度以日均消耗量(吨)计量。需要补给一个时间周期内的物资需要,且要求在岛礁剩余物资消耗完毕之前进行补充。

1.2 模型建立的变量

模型建立的数学变量见表1。

表1 变量说明Tab.1 Variable description

1.3 目标函数与约束条件

多艘补给舰从补给中心出发,遍历所有岛礁后返回当前补给中心[10],且多艘补给舰的路线不能重叠,总运输费用最小,这是典型的多旅行商(MTSP)[11-12]问题。旅行商问题是车辆路径规划问题的一种,如表1所述,点0表示出发的地点:补给中心。点1,2,…,n表示m个旅行商(补给舰)要访问的地点(某海域的各个岛礁)。

定义变量:

该问题的数学模型可表示为

目标函数:

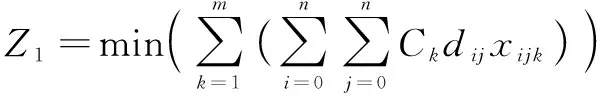
(1)

Ckdij表示第k艘运输工具经过对应弧段(i,j)所花费用(距离与运输工具k单位运输成本的乘积)。目标函数Z1表示使所有旅行商的费用最小化。

(2)

目标函数Z2表示所有岛礁剩余物资(固、液体)储存成本与补充后的物资储存成本和最小。

约束条件:

(3)

(4)

(5)

约束条件(3)表示从地点0出发,每个将被访问地点有且仅有一个旅行商经过;约束条件(4)表示任一条弧的终点仅有一个起点地方与之相连;约束条件(5)表示任一条弧的起点地方仅有一个终点地方与之相连[13]。

与此同时,还要考虑时间窗与各运输工具容量限制。各岛礁所需物资最早在其剩余物资刚消耗时进行补充,最晚于剩余物资耗尽时进行补充,再补充时可以按最大储存量进行补充。所以有以下约束条件:

(6)

(7)

(8)

约束条件(8)表示第k艘运输工具到达岛礁i的时刻加上物资装卸时间须小于岛礁i剩余物资消耗完毕所耗费的时间。因运输工具有容量限制,还有关系式:

(9)

(10)

约束条件(9)、(10)分别表示第k艘运输工具所补充岛礁液体需求量小于其最大液体载重量、最大固体载重量。

1.4 智能算法求解

如前所述,VRP问题可运用的算法有多种,但此问题有诸多的约束条件,可采用智能算法如模拟退火、禁忌算法、遗传算法(Genetic Algorithm, GA)[14]甚至是多种算法的结合进行求解。这些算法不存在对函数求导或连续性等限制,对多目标规划具有较好的全局搜索最优解能力。岛礁物资补给任务规划问题中若岛礁数量不太多时,可采用一种具有代表性的算法如GA进行求解,GA是一种智能进化算法[15],通过把问题参数编码为“染色体”,利用迭代运算方式,设定适应度函数,使经选择、交叉和变异等操作后的“染色体”最终符合优化目标。

1)染色体编码。岛礁物资补给路径规划问题可采取实数编码方式,即补给中心为0,各岛礁为1,2,…,n,编码长度为n+m。如岛礁数量为8、运输工具数量为2时,若编码为{0,1,2,5,0,3,4,6,8,7}表示路径为0-1-2-5-0和0-3-4-6-8-7-0。按此编码方式生成一定规模的初始种群。

2)适应度函数。遗传算法是一个不断从种群中选择适应度高的个体的迭代优化过程,该任务规划问题中,目标函数取极小值,故以目标函数的倒数为适应度函数F。

4)交叉算子。采取部分映射杂交,对初始解中两个基因串中的随机片断进行交叉操作,还是以n=8,m=2为例,对下列两基因中的第4、7位中间数据进行交叉,交叉后有部分数据冲突,用*表示,再采用部分映射的方法消除重复,得到以下结果。

5)变异算子。在父代基因中随机选择两个断点,将断点之间的基因逆序排列或交换断点位置,从而产生一个新的个体。

6)重新插入初始种群得到更新后的新种群。进行迭代运算,以适应度函数为选择准则,不断把问题的可行解进行收敛,从而得到最优解。

2 实例运用

根据文献[16]给出的实例,由补给中心点C为岛礁(D1～D9)运送所需物资,由A、B两种型号补给舰执行物资补给任务,每条补给舰各配备2艘小艇。补给舰回程运回固体垃圾。补给方案应包括补给舰种类、补给路线、补给数量、转运方式、物资装卸与回收材料的数量等。各岛礁(含补给中心)位置、储物情况、补给舰(艇)信息见该文献相关数据。

VRP问题中,目标函数与约束条件的处理较为复杂,总目标函数通常可取多个目标函数的加权平均,考虑约束条件时,遗传算法编码生成的初始种群及交叉(变异)后种群还要验证其是否满足约束条件,若是不可行解,需要一系列复杂的处理,总体计算量大,迭代较慢。在岛礁物资补给问题中,可以具体问题具体分析,灵活处理目标函数与约束条件。补给舰的燃油成本及各岛礁物资储存成本是一个多目标取优问题,通过计算,可发现物资储存成本远小于运输成本,故在目标函数上可以运输成本为主,为使储存成本最低,补给原则是在满足岛礁物资保障不间断的前提下尽量延长补给时间,待各岛礁剩余物资耗尽后再进行补充。与此同时,还要考虑运输工具的容量限制,基于上述分析,可运用分步优化的思路,运用智能算法先找出符合成本最低的运输路径,然后基于该路径做出微调以符合时间窗要求和为各岛礁分配物资数量。

2.1 遗传算法仿真运行结果

为任务规划的均衡性,可设定每条路线所经历的岛礁数量至少为2个以上[17]。通过编程,使用Matlab2013b程序进行仿真,得出优化结果见图1,遗传代数为25。虚粗线表示A舰航行路径C-D2-D9-D4-D3-C,实细线表示B舰航行路径C-D1-D5-D8-D6-D7-C。

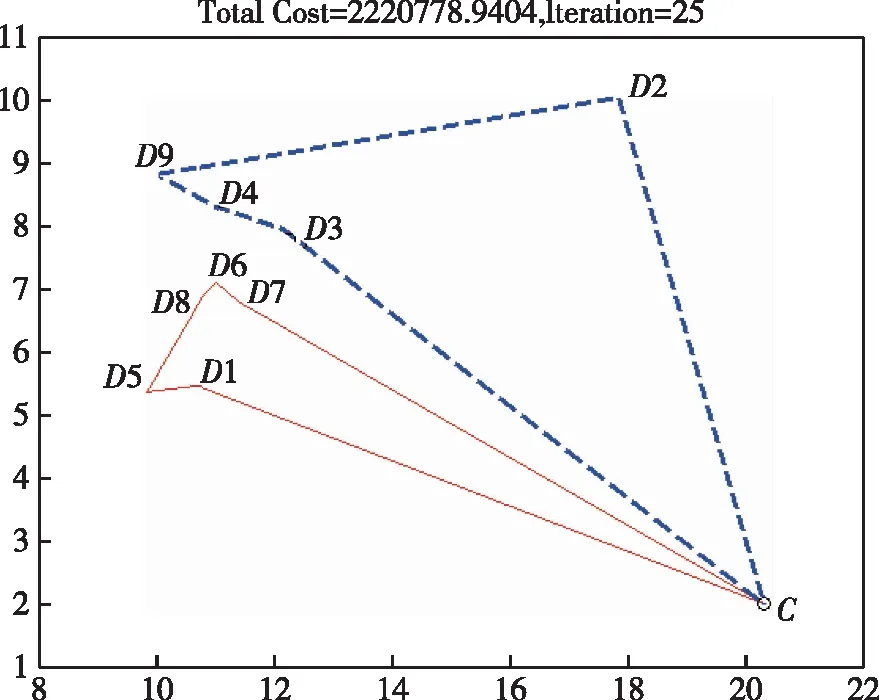
图1 双舰补给路径规划图Fig.1 Supply paths planning of dual ships

2.2 优化方案的确定

1)最优路径顺序的选择

使用A、B舰给岛礁实施物资保障时,要求使得各岛礁至少维持一个特定的供给周期。补给总的原则是:①优先补给资源即将耗尽的岛屿,如D1、D2、D3、D4等;②尽量使得补给在现有物资耗尽之后再补充,并且补充周期内所需最大库存,因为这样可以使储存成本减少;③现有库存物资与后续补充的物资可用天数之和至少能满足一个补给周期所需。

确定最优路径后,需要进一步安排A、B舰补给各岛的顺序,考虑A、B舰保障的各岛当前储存物资可消耗天数情况,在图1所示的路径基础上,应对此做出微调,A舰先保障D2,再D3,尔后D4,再D9;由于D9是小岛,应于小岛外抛锚,再由小艇倒送物资。由于D8的可维持天数较长,而D6、D7保障时效要求更强,还应对B舰路径再做出微小调整,B舰先保障D1,再D5,尔后D6,再D7;由于D8需求量不大,时间又较为宽松,可利用2艘小艇同时由D7向D8运输物资。调整后的路线为A舰的C-D2-D3-D4-D9-C,路径长1574.07海里;B舰为C-D1-D5-D6-D7-C,路径长1 288.04海里,见图2。

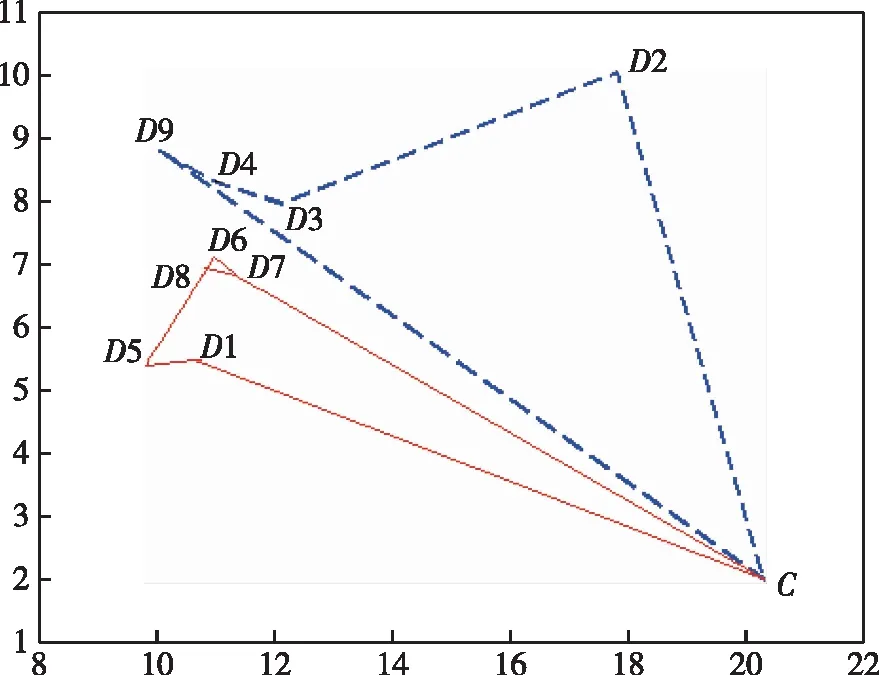
图2 调整后的优化路径Fig.2 Adjusted optimization paths

2)各岛礁物资补给的数量与时间

在规划好A、B舰路径后,物资分配应按各岛礁能支持消耗一个补给周期的量分配,即按每天的消耗水平乘以补给周期再减去当前储存量,这样可以使得补给物资满足容量限制。进一步计算A、B舰到各岛的航行时间与装卸物资时间。需要注意的是D8、D9比较特殊,对于A舰来说,需要停靠D9外某处,同时用2小艇倒运舰上物资保障D9岛所需,计算出小艇运输与装卸总耗时为17.27小时。对于B舰来说,停靠于D7后再保障D8所需,由于D8固体、液体的保障量较小,可以考虑运用2小艇来进行倒运物资,计算出总耗时为46.21小时。A、B舰到达各岛的补给量与固体回收量、航行时间与物资装卸时间计算结果见表2。

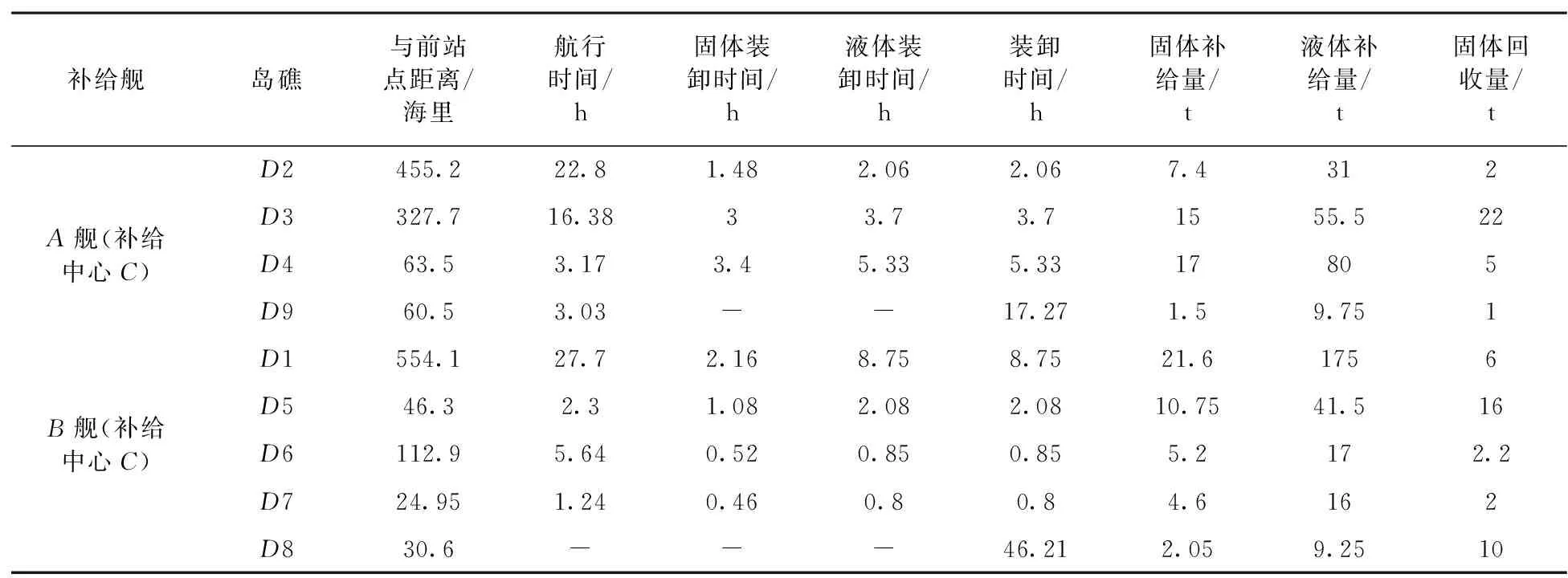
表2 A舰、B到达各岛的补给量、航行时间与物资装卸时间Tab.2 Supply volume, sailing time and material loading time of ship A and ship B arriving at each island

通过计算,A、B两舰需装载补充的固体总量为85.1 t。A舰固体量为40.9 t,B舰固体量为44.2 t。A多出的0.9 t固体可以放小艇中。A、B两舰需装载补充的液体总量为435 t。A液体量为176.25 t,B液体量为258.75 t。

3)最终方案成本分析

各岛补充后的物资储存总成本为66 690.9元。加上补充前的当前已有物资储存成本8 650.15,共75 341.05元。根据前面的优化路径,A的运输里程为1 574.07海里,B的运输里程为1 288.04海里,总费用为2 232 482元。最终的运输成本加上储存成本合计为2 307 823.05元。

3 结束语

文章建立了岛礁物资补给任务规划模型,分析了智能算法的求解过程,结合一个实例,采用算法进行仿真运算,综合利用数据分析,得出了优化方案[18-19]。方案从现实复杂问题出发,考虑保障任务较高的构成成本——岛礁物资运输成本,其次考虑储存成本、容量限制、补给周期等,分步进行优化调整,符合物资补给实际需要[20]。当然,考虑模型的拓展性,还需要进一步结合实际情况中的多种条件如天气情况对物资保障的影响,考虑把某些岛礁作为中转站进行二次补给的情况进行规划,这些还需在未来的研究中进一步深化。