基于GRU-VAE的无监督航迹异常检测方法

李 磊,张 静,欧阳齐铖,周明康

(1. 中国人民解放军战略支援部队信息工程大学,河南 郑州 450001;2. 中国通信建设第四工程局有限公司,河南 郑州 450001)

当前,外军舰机对我周边军事侦察活动日渐频繁,国家海上安全形势不容乐观,对海上高价值目标的技术侦察指挥控制是决定战争胜负的关键。如图1所示,在基于OODA环[1]的战场侦察指挥控制链中,战场态势认知至关重要。

图1 侦察指挥控制决策链Fig.1 Reconnaissance command control decision chain

战场态势认知是支撑指挥决策的重要依据。只有基于对战场当前“态”的全面理解,才能实现对战场未来“势”的准确预测与推演,从而提升战场态势理解效率。航迹异常检测技术是海上态势情报获取的关键技术之一[2-3]。充分挖掘多种渠道获取的航迹数据,掌握目标时空特征和运动模式,通过检测异常航迹,提前发现目标异常行为,可为高效侦察指挥决策提供有力支撑。通过实地调研发现,当前,在基于航迹特征的舰船异常行为检测业务上存在以下两点困难:

1)海量航迹数据大多无法准确标注其行为模式信息,导致正常航迹数据和异常航迹数据样本量极不均衡,监督学习法在此数据条件下极易出现过拟合现象,模型性能受到严重制约;

2)战场态势瞬息万变,伴随各类舰船目标行为模式的不断变化,新的异常航迹类型不断出现,过去标注的异常航迹难以表征新出现的异常航迹类型。

因此,针对海量无行为模式标签航迹数据的目标行为异常检测问题,本文方法的思路是对历史航迹数据集进行深入挖掘,建立舰船目标正常运动规律模型,通过比较实时航迹数据和模型输出的偏差发现异常航迹[4]。本文把利用历史航迹数据构建常态模型的无监督异常检测方法作为主要研究方向。

在该研究方向上,基于无监督网络模型的异常检测方法值得关注。文献[5]以自编码器(Autoencoder, AE)作为水位异常检测框架核心,通过学习正常数据的特征分布,将输出的重构损失作为异常分数并设定阈值,进而实现对水位数据的异常检测。变分自编码器(Variational Autoencoder,VAE)[6]以时间序列中潜在变量分布参数的重建概率作为异常检测的度量,不受数据结构限制,比自编码器在数据重构上更有优势。文献[7]采用变分自编码器模型对脑电数据进行异常检测,降低癫痫发作带来的安全风险。然而,以上两种模型针对航迹数据的时序建模能力还有待提高。长短时记忆网络(Long-Short Term Memory, LSTM)和门控循环单元(Gated Recurrent Unit networks, GRU)作为循环神经网络的重要变体,在时间序列建模问题上具有优势。在其他领域中,以上两种自编码器模型常配合使用以增强其时序建模能力。文献[8]提出一种基于长短时记忆网络模型LSTM的无监督异常检测模型,在此基础上,文献[9]将AE和LSTM相结合,进一步提高了模型在时序数据异常检测上的表现。文献[10]将LSTM作为VAE编码器的输入层和解码器的输出层,进一步提升了模型对时序数据的重构能力。而GRU[11]的参数量比LSTM更少,保持了LSTM的优异性能,同时其结构更加简单,过拟合风险更低,文献[12]将其应用于飞机振动数据的异常检测,并取得了良好效果。

本文构建了以GRU和VAE为主要结构元素的无监督神经网络模型,提出了一种基于GRU-VAE模型的无监督航迹异常检测方法。在模型训练阶段,使用历史航迹数据集对GRU-VAE模型进行训练,对数据集中所有航迹序列进行重构,将重构航迹序列和原始航迹序列的平均绝对距离作为模型输出的重构损失,基于输出重构损失的分布类型确定其在任意置信度下的置信区间,并将其作为航迹点重构损失门限;在异常检测阶段,该模型对实时航迹数据进行检测,将损失超出航迹点重构损失门限的航迹点视为异常航迹点,将异常航迹点占比超出阈值的航迹序列判定为异常航迹序列,再结合数据特征和重构损失异常情况向一线人员发送目标的异常行为信息。AIS数据实验结果表明,模型平均F1分数高达86.36%,查全率达95%。对比现有相关研究成果,本方法在查准率、查全率和模型F1分数上比实验性能稍次的基于长短时记忆网络的变分自编码器模型(Long-Short Term Memory-Variational Autoencoder,LSTM-VAE)方法[10]分别高出1.68%、1.18%和1.50%,对异常航迹具有高灵敏度和低漏警率,符合战场态势认知需求。

1 问题描述

针对海量无异常标签数据的航迹异常检测问题,本节在相关定义的基础上,提出对应研究思路,并对异常航迹序列进行分类。

1.1 基本定义

定义1:航迹点向量及特征

ωti=[lngi,lati,sogi,cogi]ti,分别对应的是航迹点ωti在时间戳ti的经度(lng)、纬度(lat)、速度(sog)和航向(cog)特征。其中,i是指按照时间顺序排列的航迹点序数,经度和纬度坐标是航迹点向量的位置属性特征,速度和航向是航迹点向量的运动属性特征。

定义2:航迹序列

W=(ωt1,ωt2,…,ωti,…,ωtk)是指由k个航迹点向量根据时间戳排列得到的序列。由定义1,航迹点序列W可以表示为式(1):

(1)

定义3:航迹数据集

X={W1,W2,…,Wm,…,Wn}表示由n条航迹序列组成的航迹数据集合。

定义4:异常航迹点向量

若实时航迹序列Ws经模型检测输出的重构损失序列R_Losss中存在重构损失值lossti∉[a,b],则重构损失值lossti对应的航迹点向量ωti为异常航迹点向量。

定义5:异常航迹序列

1.2 研究思路

针对海量无异常标签数据的航迹异常检测问题,本节提出基于航迹数据重构模型的无监督航迹异常检测方法系统模型,如图2所示。

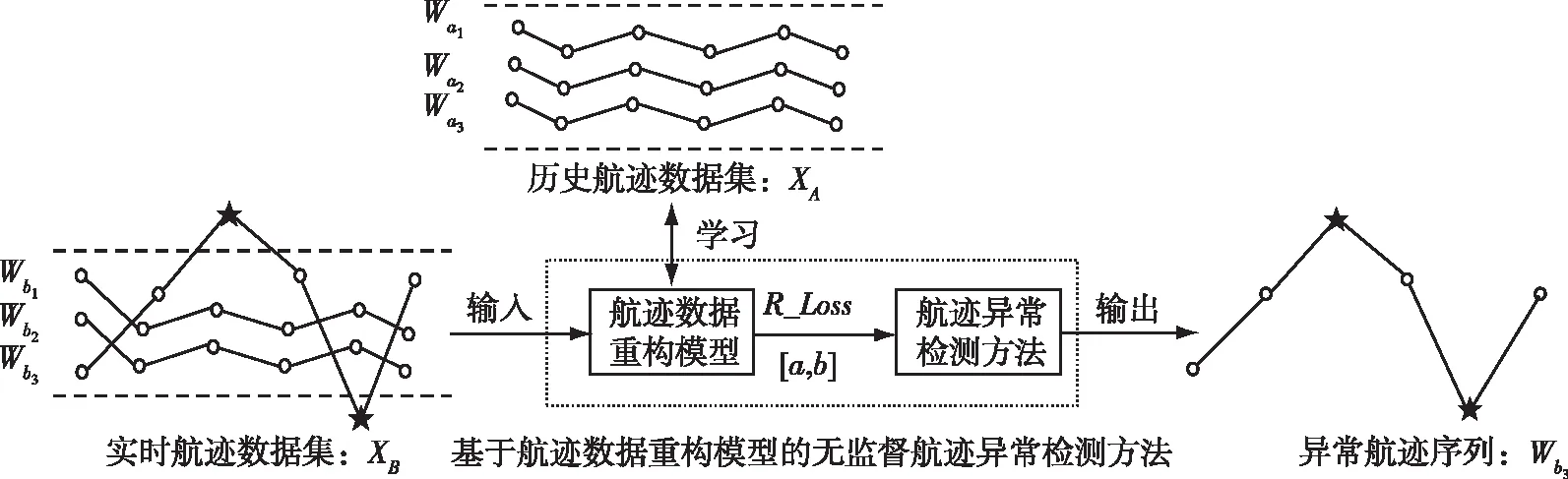
图2 研究思路Fig.2 The system model

结合1.1节基本定义,设由给定时间和空间范围内的历史航迹序列组成的历史航迹数据集为XA,实时航迹数据集为XB,集合XB中的Wb3是与历史航迹数据集行为模式不同的异常航迹序列,所有集合中的航迹数据均无异常行为模式标签。输入历史航迹数据集XA训练航迹数据重构模型后,能够输出对应的重构损失R_Losss,并据此确定航迹点重构损失门限为[a,b]。将实时航迹数据集XB中任意一条包含m个航迹点向量的实时航迹序列Ws=(ωt1,ωt2,…,ωti,…,ωtm)输入航迹数据重构模型,能够输出包含m个重构损失值的重构损失序列为R_Losss=(losst1,losst2,…,lossti,…,losstm)。

研究思路分两步:1)航迹数据重构模型通过训练学习集合XA的舰船历史航迹运动模式,根据历史航迹数据重构损失分布,确定航迹点重构损失门限[a,b];2)将集合XB中的实时航迹序列逐条输入模型,经航迹异常检测方法发现异常航迹序列Wb3。

1.3 异常航迹序列的分类

异常航迹序列可按照航迹点向量特征的分类划分为两类:1)运动异常,目标实际行为体现为舰船航速超出历史范围或短时间内变化过快,以及在侦察区域出现的短时间内航向变化过快;2)位置异常,目标实际行为体现为偏离历史航迹或出现在非法位置。本方法可检测包含其中一类异常或同时存在这两类异常的航迹序列。如图3所示。

图3 异常航迹序列的分类Fig.3 Classification of anomalous track sequences

2 方法描述

基于GRU-VAE模型的无监督航迹异常检测方法总体流程如图4所示,主要分两步:1)模型训练阶段,使用预处理后得到的历史航迹数据集训练GRU-VAE航迹数据异常检测模型,采用平均绝对误差计算重构损失,基于输出重构损失的分布类型确定重构损失的置信区间,进而确定航迹点重构损失门限;2)异常检测阶段,运用训练好的模型对预处理后的实时航迹数据集进行检测,对异常航迹序列进行深入研判,确定其异常类型。

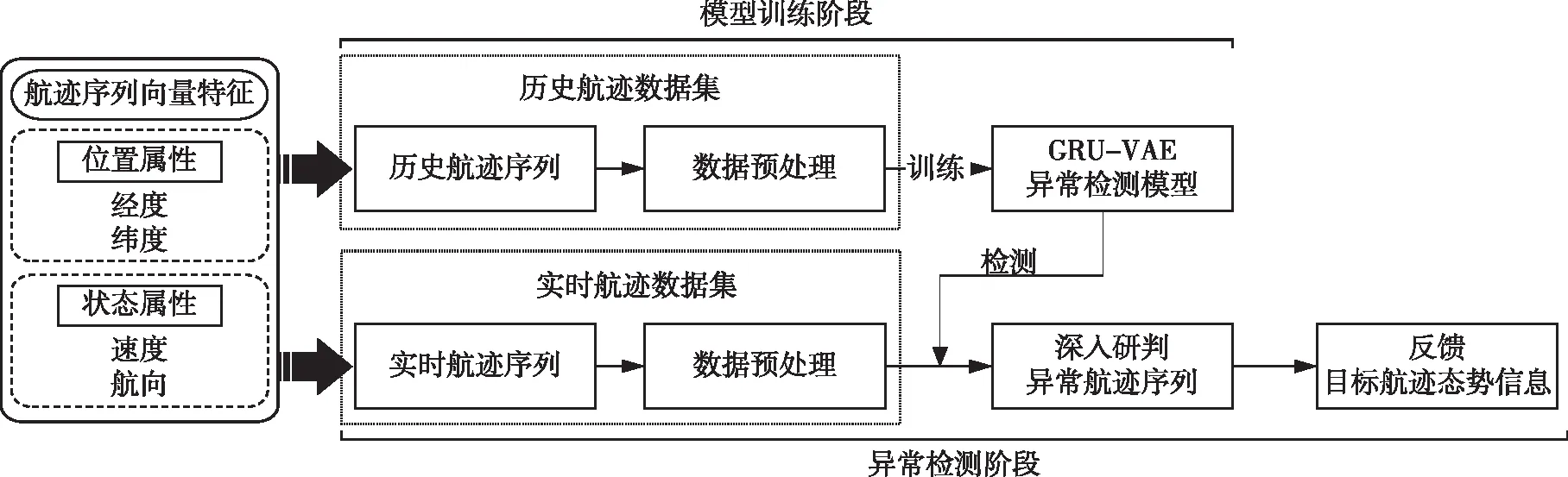
图4 方法总体思路Fig.4 Methods general idea

2.1 航迹数据集预处理

为减少数据不同量纲对深度神经网络训练的影响,使模型有效拟合训练数据,准确学习正常航迹的运动模式和规律,需要对历史航迹数据集进行预处理。历史航迹数据集的预处理流程如图5所示,分为以下4步。

图5 预处理流程Fig.5 Preprocessing process

Step 1:根据舰船类型标签,在航迹数据集中筛选出单个目标的完整航迹序列以及各时间戳下的航迹点向量;

Step 2:针对参与训练的航迹数据集,对同一目标类型的航迹序列在相同时空范围内的重复航迹予以剔除,避免深度神经网络模型训练的计算冗余或将其误识别为静止点;

Step 3:对航迹序列中航迹点向量特征值缺失的特征进行均值插值,避免数据缺失问题影响模型对常态运动模式的准确学习,均值计算式如式(2)所示:

(2)

其中,k为非缺失航迹点特征值xi的总个数。

Step4:对所有的航迹点向量特征值进行0均值标准化处理,即将航迹数据集转换为均值为0、方差为1的数据集,避免在模型训练和重构损失的计算过程中由于量纲不同、自身数值相差较大所引起的误差。先计算所有同一特征值的标准差,如式(3)所示:

(3)

其中,n为该航迹序列中航迹点向量总个数,之后运用式(4)计算标准化处理后的特征值:

(4)

式中,x指同一航迹数据集或航迹序列中航迹点向量的某特征原始值,xnew为标准化处理后得到的结果。

对需要进行检测且可能存在异常航迹的实时航迹数据集进行除Step 2之外的预处理步骤。

2.2 GRU-VAE航迹异常检测模型

本节对VAE和GRU的理论基础进行描述,并在此基础上搭建本文的GRU-VAE模型。

1)变分自编码器

VAE变分自编码器是一种无监督学习的深度神经网络模型,它基于反向传播算法和梯度下降最优化方法,利用输入数据作为监督指导神经网络训练学习实现重构输出[13]。如图6所示,变分自编码器由1个编码器和1个解码器组成,其基本思想是经过编码器函数fθ(zk)的每一个点向量X可用各航迹点向量特征值上的均值μΖ和方差σΖ表示输出的概率分布,然后,通过变分自编码器的变分推断过程,用一个近似分布p(zk)代替概率分布,并通过贝叶斯准则得到解码器输入pθ(xk|zk),最后,经解码器gθ(xk)输出重构的航迹点向量XR。

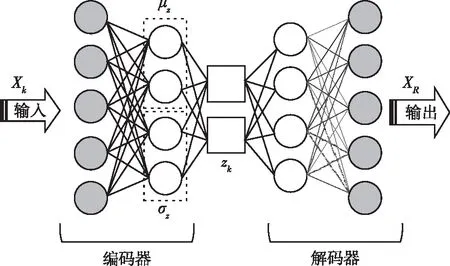
图6 VAE模型结构Fig.6 VAE model structure

在变分推断过程中,采用(Kullback-Leibler,KL)散度函数来度量两个分布之间的相似性,模型的目标函数如式(5)所示:

Loss(θ,φ;xk)=-DKL[qφ(zk|xk)||p(zk)]+

Eq[lgpθ(xk|zk)]

(5)

其中,Eq是期望的自编码重建输出特征向量;DKL是正则化项,使得qφ(zk|xk)向标准正态分布对标。为了解决神经网络反向梯度求解问题,中间采用了重参数化的操作,样本Zk从分布N(0,1)中获取变量ε,通过图6所示的期望μz和方差σz计算得到,见式(6)。

zk=μzε+σz

(6)

联立式(5)和式(6),最终的目标函数如式(7)所示。

Loss(θ,φ;xk)=-DKL[qφ(zk|xk)||p(zk)]+

Eq[lgpθ(xk|μzε+σz)]

(7)

2)门控循环单元

门控循环单元的主要功能是在数据重构过程中捕捉航迹数据的时序特性,提升数据重构的准确性。作为循环神经网络的一种变形单元,GRU门控循环单元解决了长期记忆和反向传播中的梯度消失和爆炸问题,在达到相同模型性能的前提下,其计算量小,训练效率更高[14]。图7为GRU运算示意图,它主要的功能由更新门和重置门实现,这些门结构决定了数据信息的输入、存储、遗忘和输出。

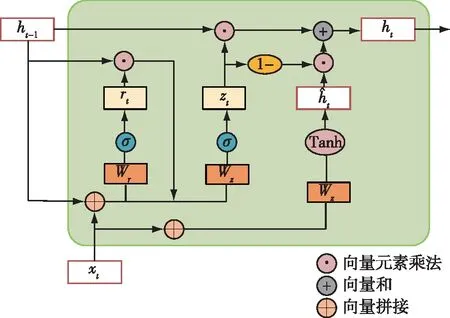
图7 GRU运算示意图Fig.7 Schematic diagram of GRU operation

图7中,ht表示GRU在t时刻状态,xt为t时间步的数据输入,σ和Tanh为非线性激活函数。式(8)～(11)展示了GRU的运算过程。Wz和bz表示更新门和重置门结构的权重和偏置,其余运算符号如图中所示。

zt=σ(Wz·[xt,ht-1]+bz)

(8)

rt=σ(Wr·[xt,ht-1]+br)

(9)

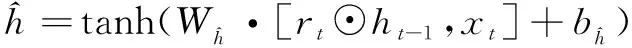
(10)

(11)

由式(10)和式(11)可见,GRU使用更新门控制输入和遗忘的平衡。当zt=0时,当前状态ht和上一状态ht-1为非线性关系;当zt=1时,ht和ht-1为线性关系。

3)GRU-VAE模型的搭建

GRU-VAE模型是在VAE框架下,将编码器输入层和解码器输出层神经元替换为GRU门控循环单元,提升了模型对航迹数据时序特征的学习能力,克服了传统循环神经网络在特征提取过程中的梯度消失和爆炸问题,实现了对数据特征的正确编码和解码。模型通过学习航迹数据的特定分布,输出得到精准的重构数据。

GRU-VAE模型的基本结构如图8所示,数据重构过程分为以下三步。首先,航迹序列W=(ω1,ω2,…,ωi,…,ωk)直接输入模型,编码器的GRU单元捕捉航迹序列点向量的时序特征,经Linear线性激活层分别输出特征值对应的均值μz和方差σz;然后,在VAE框架下进行重参数化操作,对点向量的隐变量分布Z进行估计;最后,GRU单元译码器根据隐变量Z完成对数据的时序性重构,输出重构航迹序列WR,实现端到端的数据精确重构。

图8 GRU-VAE模型基本结构图Fig.8 The basic structure of GRU-VAE model

2.3 模型训练阶段

模型训练阶段流程如图9所示。

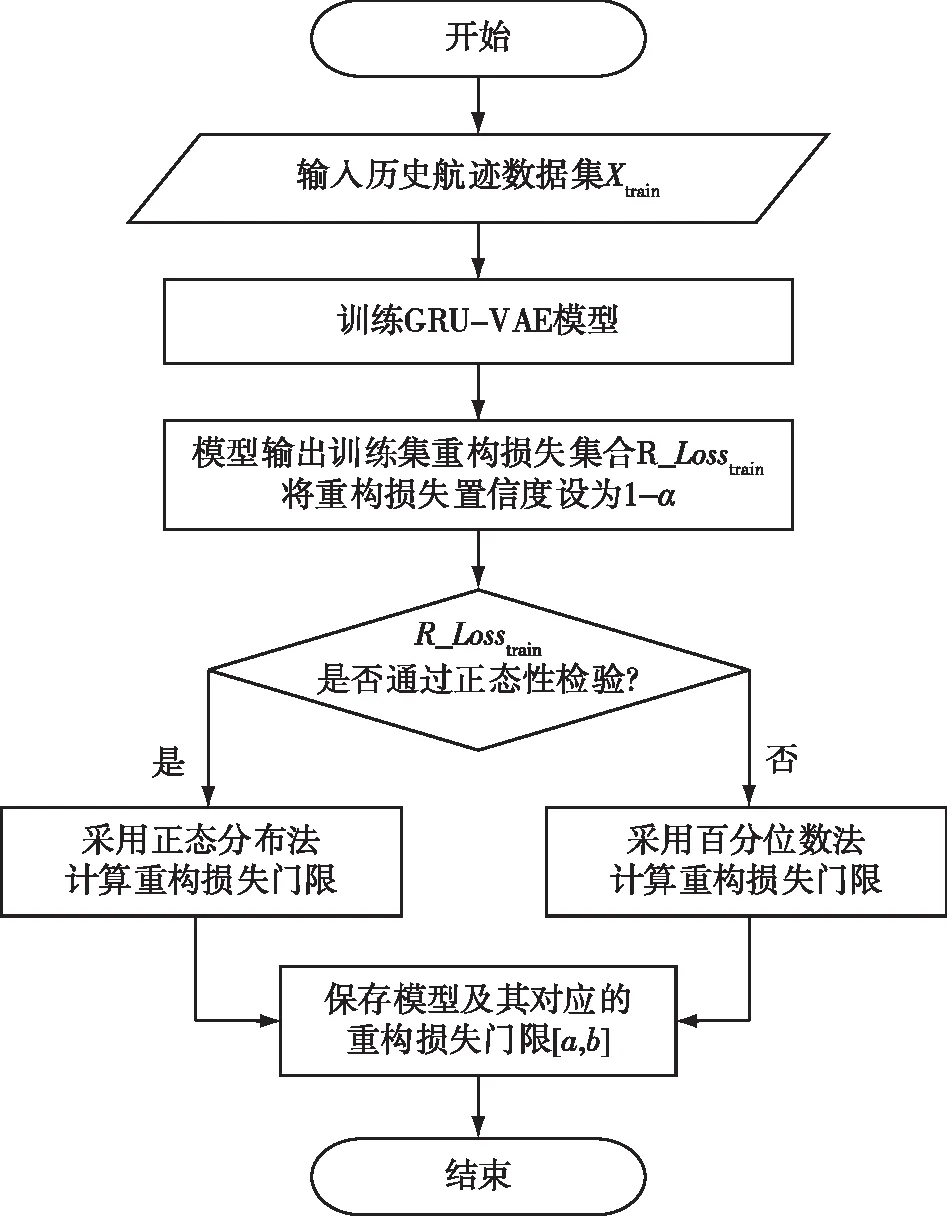
图9 方法工作流程Fig.9 Method workflow

首先,将历史航迹数据集Xtrain输入GRU-VAE模型进行训练;然后,模型输出训练集重构损失集R_Losstrain,设定重构损失的置信度为1-α;之后,对R_Losstrain进行正态性检验,结合设置的置信度,若满足正态分布,则采用正态分布法计算航迹点重构损失门限,否则,采用百分位数法计算航迹点重构损失门限;最后,保存模型及其对应的航迹点重构损失门限[a,b]。

1)重构损失计算方法

航迹序列重构损失的计算采用平均绝对误差计算方法,如式(12)所示。

(12)

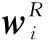
2)航迹点重构损失门限的确定

确定航迹点重构损失门限的目的是通过模型训练掌握历史航迹数据隐含的目标行为模式,为异常检测阶段提供常态基准参考。下面根据历史航迹数据输入模型得到的重构损失分布,采用正态分布法和百分位数法[15-16],对需要检测的实时航迹数据输出的重构损失值进行置信区间的估计,将置信区间作为航迹点重构损失门限。

图10为航迹点重构损失门限示意图。假设R_Losstrain服从标准正态分布,将重构损失置信度(1-α)%下的置信区间作为航迹点重构损失门限,表示为参与检测的实时航迹序列中的每个航迹点向量对应重构损失值有(1-α)%的概率会落在区间[a,b]中。

图10 航迹点重构损失门限示意图Fig.10 Diagram of area distribution of standard normal curve

若训练集重构损失序列R_Losstrain中重构损失值的分布能够通过Kolmogorov-Smirnov正态分布检验,则采用正态分布法进行置信区间的估计。

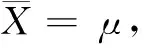
(13)

应用标准正态分布下的α分位点的定义可得

(14)

根据式(14),可以求得航迹点重构损失在任意置信度1-α下的置信区间为

(15)

其中,α为区间的显著性水平,uα/2界值可通过查标准正态分布表获得,该置信区为航迹点重构损失门限。

若重构损失分布未能通过严格的正态性检验,则采用百分位数法确定。首先,将重构损失序列R_Losstrain中的所有重构损失值按升序排列;然后,合并相同的数值并计算重构损失值lossti在重构损失序列中出现次数占全部重构损失值的比例,进而得到每个重构损失值的出现概率;最后,在已知置信度为1-α的条件下,确定航迹点重构损失出现可能性最大的区域,对称分配2个百分位数Pα/2和P1-α/2,从而确定航迹点重构损失门限为[Pα/2,P1-α/2]。

异常检测阶段将对保存的模型及其对应的航迹点重构损失门限进行调用。

2.4 异常检测阶段

异常检测阶段主要是对实时航迹序列进行检测,图11所示为具体的异常检测阶段流程。

图11 异常检测阶段流程图Fig.11 Flow chart of anomaly detection phase

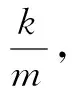
整个工作流程中,训练数据集无须人工标注,模型输入无标签数据进行无监督训练,允许训练数据中存在少量的异常航迹序列,适用于正常样本和异常样本数量悬殊的情况。

3 实验与分析

首先,对本方法的模型训练阶段进行展示,采用无标签的历史航迹数据集作为训练集对GRU-VAE模型进行训练,记录并展示模型在训练过程中目标函数值的变化情况,查看重构损失分布情况,并确定航迹点重构损失门限;然后,将重构损失置信度设为99.5%,异常航迹点占比阈值q设为0,分别采用不同的重构损失计算方法计算对应的重构损失序列并分别划定阈值上下限,对测试集进行异常检测实验,探究重构损失计算方法对异常检测模型性能的影响;接着,复现现有的基于神经网络模型数据重构的异常检测方法,使用本实验数据集进行异常检测实验,与本方法模型性能进行对比;之后,在上一步实验的基础上,探究GRU编码器隐藏神经元个数对GRU-VAE模型性能的影响;最后,探究重构损失置信度的变化对模型性能的影响。

3.1 实验条件

1)设备条件

实验设备为1台联想P920工作站,内存为64 GB,CPU主频为2.10 GHz,两张显存各为16 GB的Quadro GTX 5000显卡。在Win 10/64位操作系统上,使用Python 3.8.5编程语言,在TensorFlow深度学习框架中搭建GRU-VAE模型。

2)数据集选取

本实验采用从2019年11月1日至当年12月30日间的AIS数据作为实验对象,将地理空间范围限定在经度(-95.5°,-88°)和纬度(27.5°,33°)的美国墨西哥湾海域上,将超出AIS数据正常属性范围的数据进行剔除,再从中筛选包含客船、油船和货船三种船型的共计4 354条航迹数据作为实验数据集。按照时间先后顺序截选,本实验将2019年11月1日至12月11日的航迹数据作为训练集,12月12日至30日的航迹数据作为测试集,具体划分如表1所示。

表1 实验数据集Tab.1 Experimental dataset

为了评价无监督异常检测方法的性能,必须对测试集数据进行标注,划分正常和异常的航迹序列,以检验方法的异常检测能力。

其中,训练集包含3 454条航迹序列数据,无监督模型的训练无须对数据进行标注,经预处理后输入神经网络模型进行无监督训练。测试数据集共包含900条航迹序列。经标注,测试集包含正常航迹数据750条,异常航迹数据150条,按照舰船类型划分为三组测试集,模型性能指标参数将在三组测试集中取平均值。

测试集的标注采用以下两种方式:1)采用无监督的隔离森林算法[17]对数据进行划分,标注正常和异常标签;2)人工修改航迹序列的位置属性或运动属性,修改后的航迹数据均标注为异常数据。经标注后的异常航迹序列数据包含2.3节定义的所有航迹异常类型。

3)神经网络模型参数设置

为确保实验不受其他因素的干扰,对GRU-VAE模型参数进行统一设置。GRU-VAE神经网络模型的相关参数如表2所示。其中,梯度优化函数采用Adam优化算法,学习率设置为0.001,模型的目标函数按照式(5)设置。

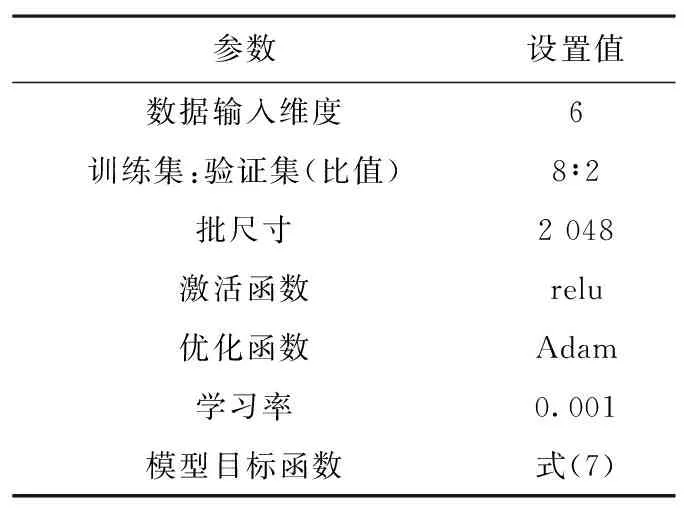
表2 模型参数设置Tab.2 Model parameter setting

由于需要探究GRU隐含层神经元个数对模型性能的影响,故在前面的实验中,将GRU隐含层神经元个数设置为固定值40。

3.2 评估指标

采用查准率P、查全率R和F1分数对异常检测模型性能进行评估,如式(16)～(18)所示。

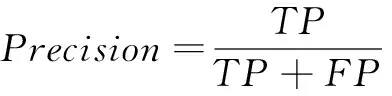
(16)

(17)

(18)

其中,TP表示被模型预测为异常的异常样本,TN表示被模型预测为正常的正常样本,FP表示被模型预测为异常的正常样本,FN表示被模型预测为正常的异常样本。

采用虚警率FPR和漏警率FNR对异常检测方法性能进行评估,如式(19)、(20)所示。

(19)

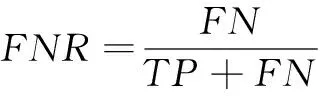
(20)

3.3 实验过程

1)模型训练阶段

本节对本方法的模型训练阶段进行展示,并示例说明重构损失的阈值上下限的划定方法。先在Tensorflow深度学习框架下搭建GRU-VAE网络模型,后将训练集输入模型进行训练。图12展示了模型训练过程中,训练集和验证集目标函数值随训练轮数的变化情况,可见模型在500轮内稳定收敛,对训练数据集进行了充分拟合。

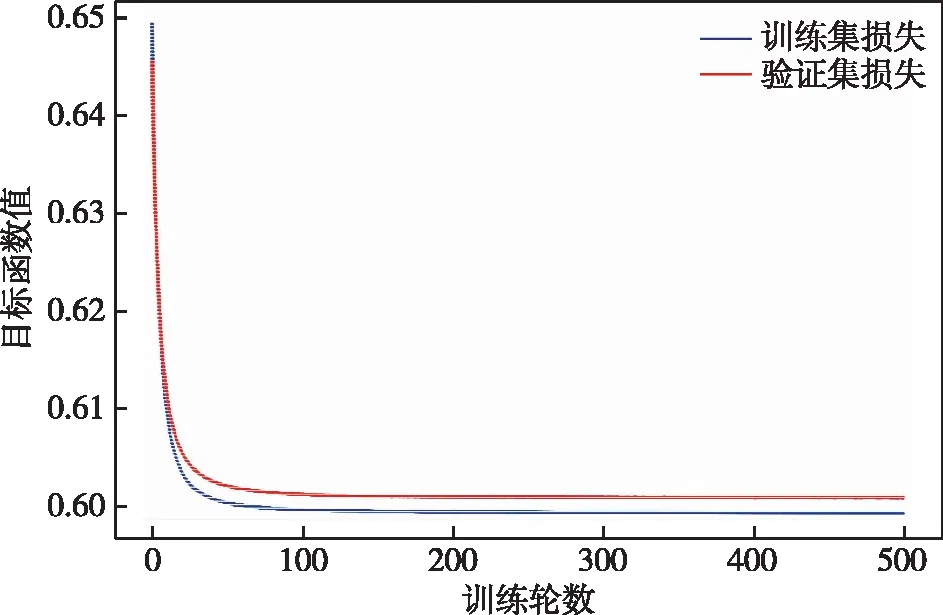
图12 模型损失值变化Fig.12 Model loss value changes

图13利用高斯核密度估计曲线和直方图对三种船型训练集的重构损失序列的分布情况进行展示。下面以计算客船训练集的航迹点重构损失门限过程为例。

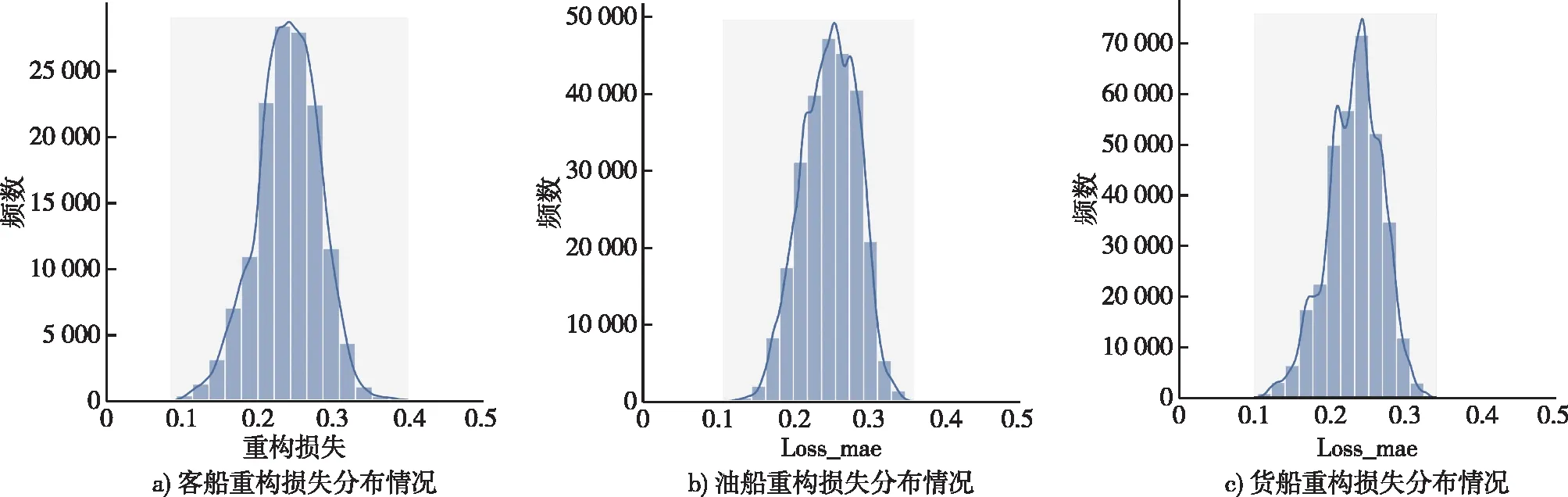
图13 三种船型训练集的重构损失序列直方图和核密度曲线展示Fig.13 The reconstructed loss sequence histogram and kernel density curve of the training set of three ship types are displayed

对客船航迹数据集的重构损失序列进行对数变换后,模型能够通过正态性检验,且采用平均绝对误差计算方法得到的重构损失序列分布均可拟合正态分布,下面采用正态分布法确定航迹点重构损失门限。本文中置信度设定为99.5%,以采用绝对平均误差计算方法计算重构损失序列为例,输出的重构损失序列中共有137 214 个航迹点向量,重构损失均值为0.241 4,标准差为0.041 9,置信度为0.995时,查标准正态分布表有uα/2=2.58,根据本方法可算得重构损失的置信区间为[0.133 3,0.349 5],阈值上限为0.349 5,阈值下限为0.133 3,表示参与检测的航迹序列中,每个航迹点向量所对应的重构损失值有99.5%的概率会落在区间[0.133 3,0.349 5]中。

2)重构损失计算方法对模型性能的影响

为选择更合适的重构损失计算方法,实验探究了重构损失计算方法对模型异常检测性能的影响。除平均绝对误差计算方法外,分别使用平均绝对百分比误差和均方误差计算重构损失,分别如式(21)和式(22)所示。

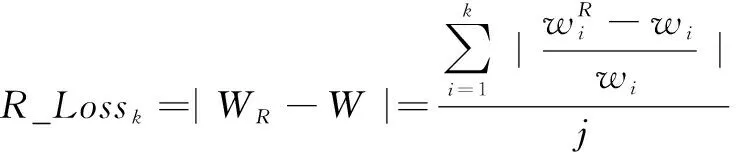
(21)

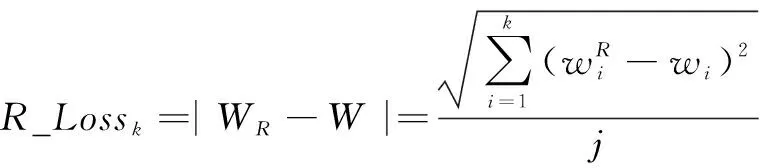
(22)

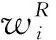
实验将本方法工作流程中的异常航迹点占比阈值z设为0,即只要存在异常航迹点向量则将该航迹序列判定为异常航迹。在航迹点重构损失置信度为99.5%的条件下,分别记录模型在三组测试数据集上的平均查准率、平均查全率和平均F1分数,如表3所示。

表3记录了在不同重构损失计算方法下的模型平均性能,采用平均绝对误差计算重构损失的模型平均查准率、平均查全率和平均F1分数分别比采用均方误差计算方法的模型高2.39%、1.00%和1.85%。可见,基于该实验数据集,本方法采用平均绝对距离计算重构损失的模型性能最好。

3)类似方法性能比较

为了验证本方法在性能上的优势,本节对现有的基于数据重构模型的异常检测方法进行了复现,表4记录了性能对比情况。

表4 基于数据重构模型的异常检测方法性能对比Tab.4 Performance comparison of anomaly detection methods based on data reconstruction

如表4所示,文献[8-9,18]分别提出了基于自编码器网络、深度长短时记忆网络以及将两种网络相结合的方法,但在本实验数据集上的实验性能相对较差,模型的F1分数均未超过70%。文献[10]、文献[19]和本文方法采用了变分自编码器后,模型性能提升明显,F1分数均在80%以上。本方法将GRU门控循环单元作为变分自编码器的输入层和输出层,使得本文提出的GRU-VAE模型在查准率、查全率和模型F1分数上分别比文献[10]提出的LSTM-VAE模型高1.68%、1.18%和1.50%,可见引入GRU模块可有效提高模型的异常检测性能。综上,本方法采用的GRU-VAE模型在解决航迹异常检测问题上具有性能优势。

4) GRU编码器隐藏神经元个数对模型性能的影响对比

为了对比GRU编码器隐藏神经元个数对模型性能的影响,基于上一步实验得到的性能最佳模型,本节采用平均绝对误差计算重构损失,并在重构损失置信度为99.5%的条件下划定航迹点重构损失门限,在本实验数据集中进行异常检测实验,探究GRU编码器隐藏神经元个数变化对模型性能的影响。实验得到的模型平均F1分数对比情况如图14所示。

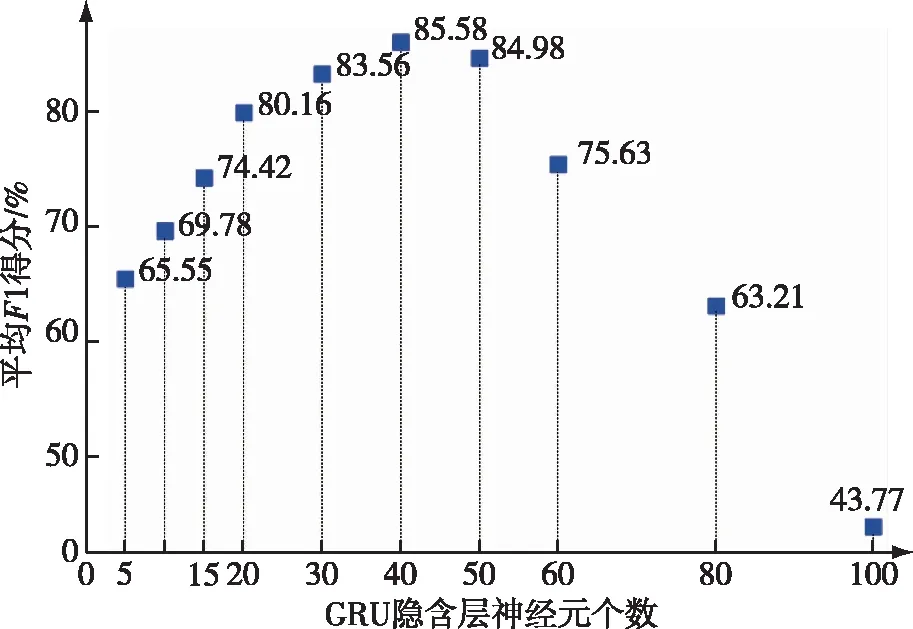
图14 平均F1分数随GRU隐含层神经元个数变化情况Fig.14 Variation of average F1 score with the number of neurons in GRU hidden layer

由图14可见,当GRU编码器隐藏神经元个数由5开始逐渐增加时,模型平均F1分数随之提高,可见适当增加GRU编码器隐藏神经元个数对模型性能具有提升作用。当数目为40时,模型性能最好,F1分数高达85.58%。GRU隐含层神经元个数继续增多,使得模型参与训练的参数增多,无法很好地拟合数据集,导致模型平均F1分数逐渐降低。当个数为80时模型平均F1分数为63.21,比隐含层神经元个数为5时的模型得分还要低2.34。

5) 重构损失置信度对模型性能的影响

根据本方法提出的异常检测方法流程,理论上重构损失置信度越高,其门限则越大,对应的查准率随置信度增大而增大,查全率对应减小。为了进一步探究重构损失置信度的设置对模型性能的影响,本节实验对不同重构损失置信度下的模型性能进行对比,进一步总结本方法的实际应用要点。

本节实验将异常航迹点占比阈值q设为0,分别在置信度为95%、97%、99%、99.5%和99.99%的条件下设定航迹点重构损失门限,对三组测试数据集进行异常检测实验,记录模型的平均查准率、平均查全率、平均F1分数、平均漏警率和平均虚警率的变化情况,实验结果如图15和16所示。

图15 模型查准率、查全率和F1分数随置信度的变化情况Fig.15 Model precision, recall and F1 score change with confidence

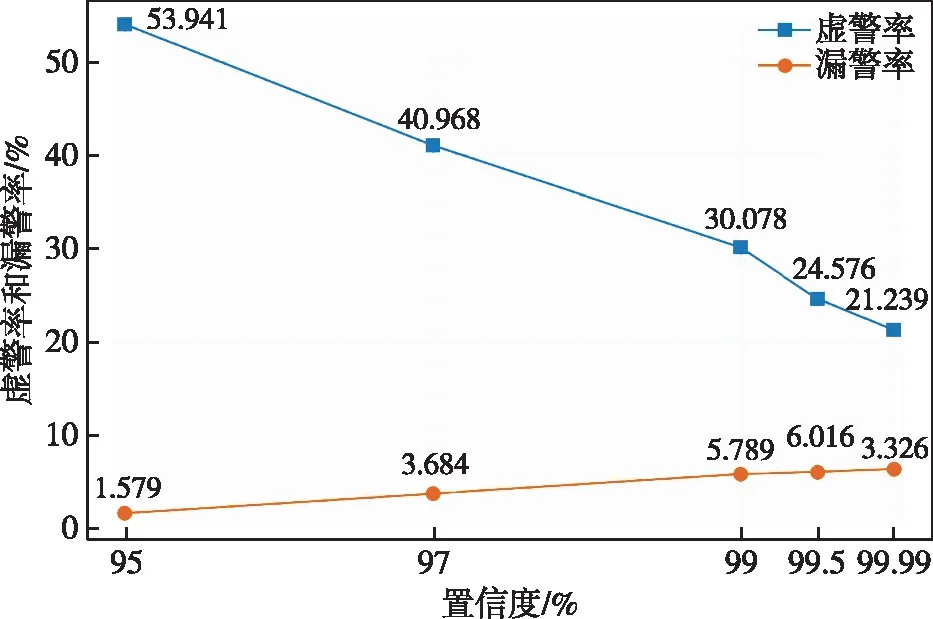
图16 模型虚警率和漏警率随置信度变化情况Fig.16 The false alarm rate and missing alarm rate of the model change with confidence degree

根据以上实验结果,可得出以下结论:

①模型的F1分数随着置信度的增大而增大,在重构损失置信度为99.99%时F1分数最高,为85.58。结果表明,设置的重构损失置信度越大,模型的异常检测性能越好。

②根据本文提出的异常检测方法,理论上设置的航迹点重构损失置信度越高,其重构损失门限则越大,对应的查准率随置信度增大而增大,查全率随置信度增大而减小,实验结果验证了这一点。

③模型平均漏警率和重构损失置信度呈正相关,所有参与实验的置信度对应的平均漏警率均在7%以下,可见本模型对异常航迹的检测较为灵敏。

④模型平均虚警率和重构损失置信度呈负相关,然而最大和最小虚警率之间相差32.7%,可见重构损失置信度的设置对模型虚警率影响较大。

综上,针对一线侦察应用场景,虽然重构损失置信度过低会使方法的虚警率较高,耗费人员精力对检测出的异常航迹进行甄别,但本方法较低的漏警率可使在一线侦察业务流程中不错过任何一个可疑的运动目标,及时从异常航迹中发现战场态势变化,符合一线单位侦察需求。

6) 异常航迹类型研判过程

本节选取两条在前文异常检测实验中被判定为异常的航迹作为实验素材,展示本方法对异常航迹的研判过程。依据前文关于航迹异常检测阶段的理论描述,重构损失置信度设置为99.5%,将异常航迹点占比阈值q设为0,即存在异常航迹点就将其判定为异常航迹序列,对异常航迹进行深入研判。按照航迹的异常类型,分别对不同类型的异常航迹研判过程进行展示。

①运动异常航迹的检测

在前文实验中,MMSI号为210959000的货船航迹被检测为异常航迹,异常类型的研判过程分为以下三步。

首先,对该航迹序列的重构损失和向量特征随时间的变化情况进行可视化,结果如图17所示。红色方框标注了超出航迹点重构损失门限的部分,对应可以查看超出部分所处的时间段。同时展示的航迹序列所有向量特征随时间的变化情况无法发现导致重构损失值超限的对应特征。

图17 重构损失和向量特征随时间变化情况Fig.17 Reconstruction loss and vector feature change over time

然后,对该船航迹序列和历史航迹数据集中具有相近航道的航迹序列在地图上可视化展示,结果如图18所示。红色航迹线是该船在地图上呈现的实际航迹,绿色区域是历史航迹数据集中具有相近航道的航迹覆盖区域。由图18可知,该货船航迹基本在绿色区域中活动,与历史航迹基本吻合,无明显位置异常迹象。

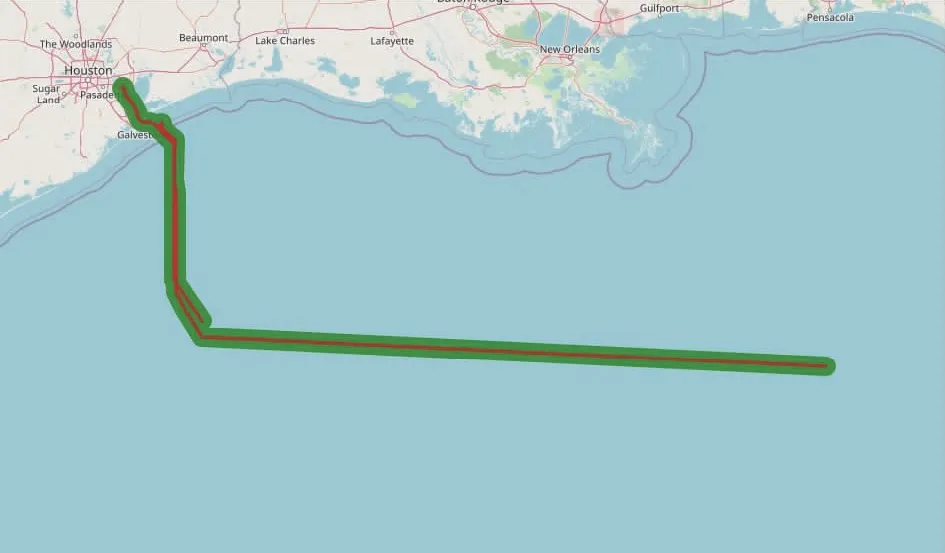
图18 运动异常航迹的可视化Fig.18 Visualization of abnormal trajectories in motion

最后,操纵动态可视化图,逐个展示航迹向量特征随时间的变化情况。图19为航向变化率随时间的变化情况,可发现航向变化率曲线的异常突起时间段和重构损失超限时间段相一致。综上,可以判定该货船航迹序列为运动异常航迹序列,异常原因为航向在短时间内的快速变化。

图19 航向变化率随时间的变化情况Fig.19 Course change rate over time

②位置异常航迹的检测

在前文实验中,MMSI号为353325000的货船航迹被检测为异常航迹,异常类型的研判过程同上节。

首先,通过图20查看了该航迹序列的重构损失和向量特征随时间的变化情况,可以看到,在2019年12月3日晚23点39分至次日的0点17分,重构损失超出了阈值上限。

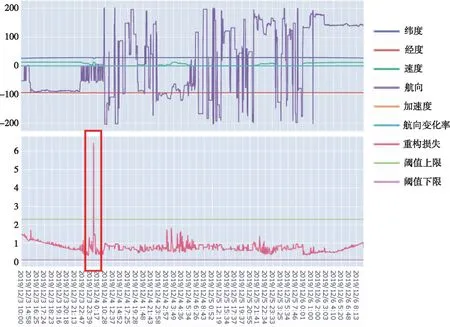
图20 重构损失和向量特征随时间变化情况Fig.20 Reconstruction loss and vector feature change over time

然后,查看航迹序列在地图上的可视化情况,如图21所示,并和历史航迹数据集中具有相近航道的航迹进行对比,可以看到,有部分航迹点位置偏离历史航迹所经区域,初步可判定为是位置异常航迹。

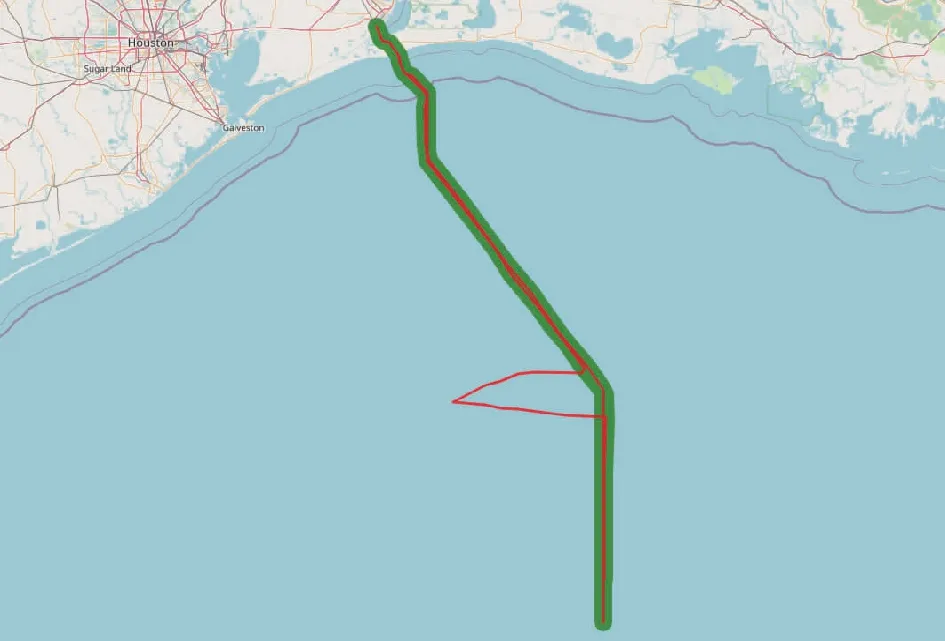
图21 位置异常航迹的可视化Fig.21 Visualization of anomalous track in position

最后,通过图22查看各航迹向量特征值随时间的变化情况,经度的变化和重构损失的超限时间范围相吻合。综上研判,该航迹序列判定为位置异常航迹,异常表现为偏离历史航迹所在区域。

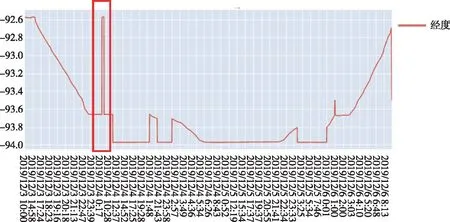
图22 经度随时间的变化情况Fig.22 Longitude changes over time

4 结束语

针对海量无异常信息标签航迹数据的目标行为异常检测问题,提出一种基于GRU-VAE模型的无监督航迹异常检测方法。该方法引入GRU门控循环单元提升VAE变分自编码器模型的时序建模能力,利用无异常信息标签的历史航迹数据对模型进行训练,采用正态分布法或百分位数法将指定置信度下的置信区间作为航迹点重构损失门限,结合实时航迹序列的重构损失值超限和异常航迹点占比情况检测出异常航迹。通过实验证明本方法可实现对无行为模式标签的航迹数据进行异常检测,与现有的基于数据重构模型的无监督航迹异常检测方法相比,具有性能优势,对异常航迹的检测具有高灵敏度和低漏警率,基本满足战场态势认知需求。