融合容错控制理论的火力分配优化策略*

伍晓龙,杨 悦,卢慧敏

(海军大连舰艇学院,辽宁 大连 116018)

火力分配是兵力对抗的核心内容,构建合理科学的火力分配模型以及寻求相应的求解方法十分关键。该类问题属于经典的多目标规划问题,解决该类问题的方法一般有神经网络算法[1]、动态规划法[2]和遗传算法[3-4]等。但在兵力对抗中,战场实时因素考虑较多,实际火力打击策略往往不能够按照预期进行,在火力打击的过程中,误差是不可避免的。谢峰[3]采用并列式遗传算法,提高了搜索的速度;曲相宇[4]对遗传算法中的选择排序环节进行了创新,能够更好地判断策略的优劣。上述文献中均假设火力单元弹药充足,但是实际中火力单元弹药储备是有限的,火力单元在拦截目标时可能存在失误的情况,目标的适应度函数不能很好地反映存在失误的情况下火力打击分配策略的优劣。本文考虑误差因素,提出一种结合容错控制的火力分配最优化策略,在保证整体策略的最优化的同时,能通过自适应容错控制律,实现整体策略的容错度最大化。

1 模型介绍

1.1 火力分配模型

火力分配应充分考虑各种武器的毁伤效率、目标的易损性和毁伤等级。现代战争中,既要考虑打击目标的毁伤程度,又需要综合考虑拦截目标的威胁程度,以此来判断火力打击的优先等级[5]。除此之外,考虑火力单元弹药储备是有限的,火力单元未能拦截目标等实际情况,故火力分配策略上存在一定失误概率。

假设m个舰艇组成的编队(m个火力单元组成的火力单元集)对n批目标进行拦截。在拦截前已经对各批目标的价值、目标的威胁度、各个火力单元对拦截各批目标的射击有利程度、各个火力单元对拦截目标的命中概率做了量化处理,并且各个火力单元的弹药储备已知。第j批目标对第i个火力单元的价值评估为wij,第j批目标对第i个火力单元威胁评估值为tij,第i个火力单元对第j批拦截目标射击有利程度估计值为pij,第i个火力单元对第j个拦截目标的拦截概率为qij。

因此效益值为:

cij=wijpijqij

(1)

eij=tij(1-qij)pij

(2)

式中,cij为第i个火力单元拦截第j批目标时的收益大小;eij为第i个火力单元拦截第j批目标时的威胁程度大小。

1.2 火力分配原则

1.2.1 高威胁目标优先攻击原则

在火力对抗过程中,保证我方舰艇作战能力,实现持续作战是一个关键的问题。因此,当出现高威胁目标时,编队将进行优先打击。

打击优先级与威胁程度关系如下:

(3)

对于高威胁目标,将由射击有利程度最高的舰艇进行打击。

1.2.2 高效益目标集火攻击原则

在火力对抗过程中,在火力盈余的情况下针对高效益目标采取集火攻击原则,对于高效益目标评价标准如下:

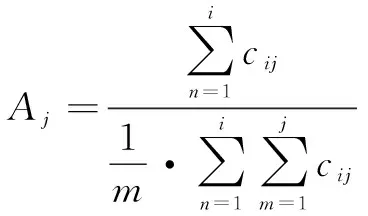
(4)

集火攻击均是在火力盈余的情况下进行考虑的内容,因此定义高效益目标与一般效益目标如下:

当A>2.0时,为高价值目标,对于该目标分配3个火力单元,一般而言,高价值目标个数不超过总目标个数的10%。

当2.0≥A>1.5时,为中价值目标,对于该目标分配2个火力单元,一般而言,中价值目标个数不超过总目标个数的15%。

其余目标为一般价值目标,对于该目标分配1个火力单元。

1.2.3 整体分配最优原则

分配目标时应当充分考虑火力打击的整体协同优势,使整体的打击效果达到最佳的同时,也要保证整体受到的威胁程度最小。

舰艇火力分配原则应满足:

1)对敌火力打击效益值最大;

2)我方受到威胁程度最小。

可建立如下多目标规划问题:

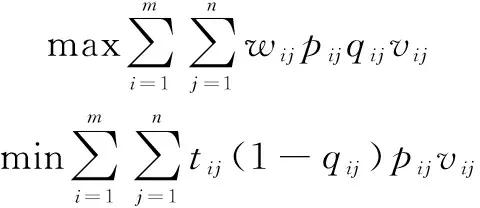
(5)

式中,vij=1为第i个火力单元对第j批目标进行拦截,vij=0为第i个火力单元未对第j批目标进行拦截。

限制条件为:

(6)

(7)

式(6)表示每批目标分配M个火力单元,式(7)表示每个火力单元最多只能射击Si批目标。

1.3 容错控制律

该问题是多目标优化问题,考虑拦截概率,通常采用平均最优分配方法,得到平均的最优值。受拦截概率的影响,实际情况与理想方法会有一定偏差,本文考虑拦截概率的影响,在部分火力单元未完成拦截任务时,能够及时采取反应,最大程度降低失误带来的损失。

火力打击单元的火力打击分配方案在进化算法中可以视作一个基因,在容错控制系统中可以视作一个执行器,例如一艘舰艇计划攻击序列1和序列3的目标,则其对应的火力分配策略为[1 3],如果由于失误导致该艘舰艇未能打击序列3的目标,则认为该艘舰艇的第2个火力打击单元发生失误(序列3位于策略的第2位)。

以此类推,若第i个火力打击单元发生失误,可以视为第i个执行器发生故障。

针对容错控制系统:

(8)

第i个执行器故障形式为

ui=σiμci

(9)

式中,ui为第i个执行器实际输出,μci为第i个执行器的理想控制输入,0≤σi≤1为执行器失效的程度。

针对火力分配的实际情况,制订如下容错控制原则:

1)第i个执行器发生故障时,只能从第i+1个执行器及以后进行补偿,即当某个火力打击单元发生故障时,调用其他火力打击单元进行补偿。

2)为避免失误过多打乱原本的作战计划,尽可能通过提高单个执行器补偿幅度进行容错控制,即通过提高单个火力单元的作战效能进行补偿,而非过多改变原有计划。

2 算法设计

火力分配问题属于决策优化问题,在进行火力分配时,需要根据各火力单元以及拦截目标的具体情况进行决策。实际战场中拦截失误是经常出现的,因此火力分配策略在满足毁伤效能最优化的同时,也需要保证较大的容错度,具有较大容错度的火力分配策略更加符合战场需要。

本文构建的基于容错控制的火力分配策略,是结合分布式遗传进化原理和自适应容错控制理论的分配策略。种群在各自环境中得到进化的优秀子代种群合并后,会产生容错度和适应值都较高的下一代。将每一种体能分配策略视作一个系统,制定相应的容错控制律,评估系统在出现误差时的恢复与补偿情况。接下来给出具体算法。

2.1 编码

编码是遗传空间到问题空间的映射。火力打击中,舰艇需要进行火力分配的火力单元较多,为了能够更加清晰地反映火力分配方案,本文采用十进制编码方式,染色体的长度由舰艇的具体火力单元数量决定,基因则代表火力分配方案。例如3个舰艇分别具有不同数量的火力单元,数量分别为1、2、3,当有4个拦截目标时,染色体编码为[1 2 0 0 4 3]代表一种火力分配方式,第1艘舰艇的火力单元为[1],即第1艘舰艇的第1个火力单元打击序列1的拦截目标,第2艘舰艇的火力单元为[2 0],即第2艘舰艇的第1个火力单元打击序列为2的拦截目标,第2个火力单元没有打击目标,第3艘舰艇的火力单元为[0 4 3],即第3艘舰艇的第1个火力单元没有打击目标,第2个火力单元打击序列为4的拦截目标,第3艘舰艇的第3个火力单元打击序列为3的拦截目标。

2.2 初始化种群

根据目标函数类别进行分组,产生相应的子种群,使各子种群能够同步进行寻找最优解。本文主要根据打击效益和威胁程度进行寻优,因此将初始种群分成两个子种群。

2.3 交叉

本文采用随机多点间基因互换进行交叉,有效提高算法收敛的速度。对于产生的个体,直接用子代替代父代,容易出现局部过早收敛的情况。本文引入模拟退火算法进行改进,通过合理的降温途径,在迭代的前中期保留一定的“潜力解”,一定程度上提升了算法全局搜索能力,避免产生局部最优解[6]。

2.4 变异

传统的遗传算法一般采用固定变异概率,本文为了增大搜索范围,减少搜索时间,采用可变的自适应概率变异方法。在迭代的初期具有较大的变异概率,保证个体的多样性;在迭代后期具有较小的变异概率,保证算法尽快收敛[7]。自适应变异概率公式为

(10)

式中,Pk表示第k代变异概率;Pmax和Pmin分别表示最大和最小变异概率;Kmax表示最大迭代次数。

2.5 选择

为防止当前群体的最优个体在下一代丢失,并且增加遗传算法的收敛速度,将上一代群体中的最优个体不进行交叉变异操作直接遗传到下一代。本文采用自适应的精英策略,在迭代的初期,精英个体保留数量较少,在迭代的后期,精英个体保留的数量会增多[8]。自适应精英策略的保留公式为

(11)

式中,Jk表示第k代精英个体的保留个数;Jmax和Jmin分别表示最大和最小变异概率;Kmax表示最大迭代次数。

2.6 容错控制

当遗传算法确定初步最优策略后,可以将火力部署策略视作完整系统,拦截失误可以视作对系统产生的扰动。通过制定容错控制律,尽可能将扰动所带来的损失降到最小,同时将补偿代价降到最低[9]。

为适当简化模型,做如下假设:

1)每次实验出现至多两次失误;

2)失误概率能够根据实际情况具体给出,在整体建模过程中不再变化;

3)优先选择空余且效益值和威胁值最接近失误单元的火力单元。

制定容错控制律[10]如下:

Δm=ma-mb

(12)

(13)

式中,Δm表示出现失误时,理想情况与实际情况差值;ma表示理想情况下适应值;mb表示实际情况适应值;Δ(wijxij)表示第i个火力单元拦截第j个目标时,后续执行器与失误执行器差值,式(13)表示第k个执行器失误时,后续执行器补偿情况。

当制定初始最优策略后,会进行100次容错实验,以此评估策略的优劣,同时得到相应的补偿方案。具体的算法流程图见图1。

图1 算法流程图Fig.1 Algorithm flow chart

3 仿真验证与结果分析

为了验证模型的可靠性和合理性,假设我方舰艇数量为7艘,每艘舰艇各有两个火力单元,敌方需要拦截的目标有10个,将有4个单元的火力盈余,我方舰艇对各目标的射击有利程度、威胁程度、目标价值、拦截概率如表1～表4所示。

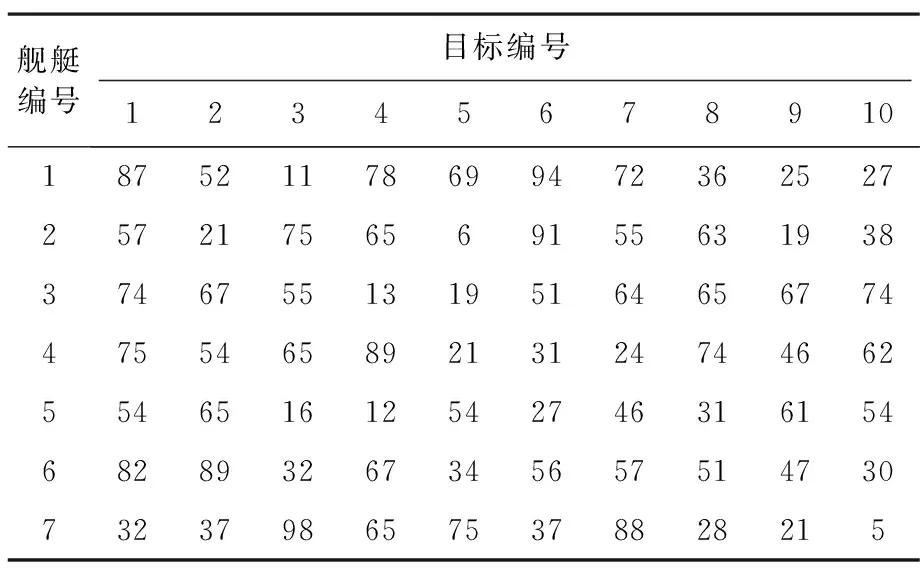
表1 射击有利程度Tab.1 Shooting advantage

表2 威胁程度Tab.2 Threat level

表3 目标价值Tab.3 Target value

表4 拦截概率Tab.4 Interception probability

对上述信息进行分析处理,得到目标的打击次序为[4 9 8 1 5 3 2 6 10 7],其中效益目标为5和3。

采用分布式遗传算法求解该问题,遗传算法中个体数量为100,将种群分为两个子种群,最大遗传次数为100次,采用多点随机交叉,初始交叉概率为0.85,初始退火温度为1 000度,最大变异概率为0.1,最小变异概率为0.01,最大精英个体保留个数为10个,最小精英个体保留个数为5个。

迭代100次后,我方收益—迭代次数函数图见图2,威胁程度—迭代次数函数图见图3,我方净收益—迭代函数图见图4,最终种群函数值变化见图5。图2、图3、图4中,种群在86代后能够迭代到最优值且趋于稳定,其中目标收益最大值为34 125,威胁程度最小值为4 847,净收益最大值为29 278。由图5可以看出,最终种群中个体完全相同,达到了目标收益最大值和威胁程度最小值。

图2 收益—迭代函数图Fig.2 Revenue iteration function

图3 威胁程度—迭代函数图Fig.3 Threat level-iterative function

图4 净收益—迭代函数图Fig.4 Net income iterative function

图5 个体函数值变化图Fig.5 Individual function value change

初步得到目标分配方案如表5所示。

表5 目标分配方案Tab.5 Target allocation scheme

得到初步方案后,分别考虑拦截失误一次和两次的情况,以此来验证容错控制的可靠性。

存在一次失误时,进行100次重复实验,进行容错控制之后,收益前后对比图见图6,威胁前后对比图见图7,分析可得,容错控制能够最大程度地减少收益损失,最小程度地提升威胁程度,能够体现容错控制的效果较好。

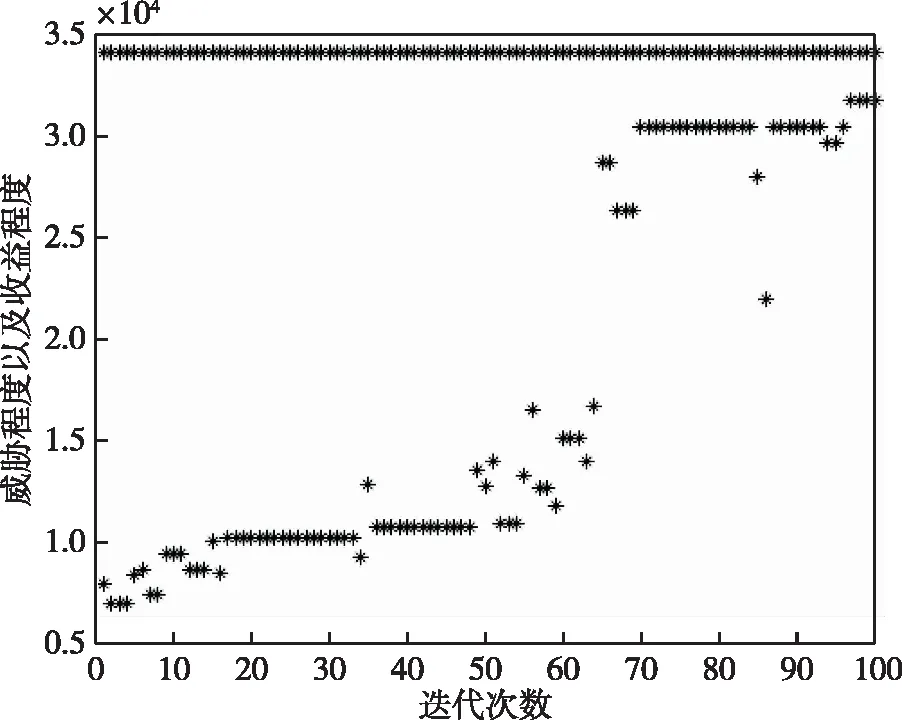
图6 一次失误时容错控制后目标收益图Fig.6 Target income after fault-tolerant control in case of one fault

图7 一次失误时容错控制后威胁程度图Fig.7 Threat degree diagram after fault tolerance control in case of one fault

存在两次失误时,进行100次重复实验,进行容错控制之后,收益前后对比图见图8,威胁前后对比图见图9,分析可得,容错控制后能够保证前后目标收益差值最小,前后威胁程度差值最小,也反映了容错控制效果较好。

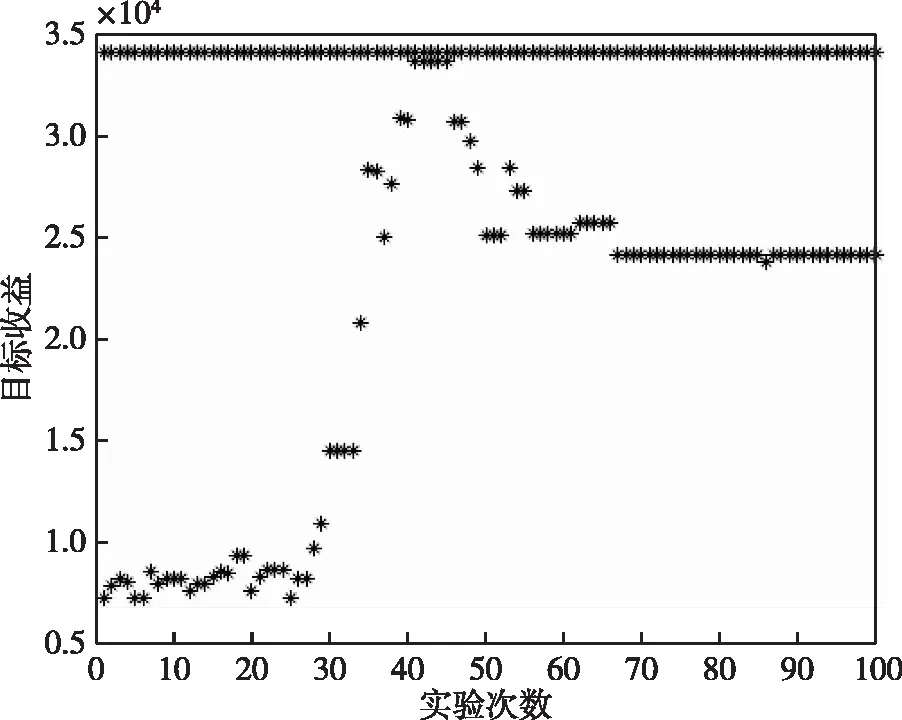
图8 两次失误时容错控制后目标收益图Fig.8 Target income diagram after fault-tolerant control in case of two faults

图9 两次失误时容错控制后威胁程度图Fig.9 Threat degree after fault tolerance control in case of two faults

4 结束语

本文结合遗传算法与容错控制理论对火力打击问题进行求解,该算法的优点在于考虑了拦截失误的情况,能够更好地反映战场真实情况。在遗传算法中结合了模拟退火算法和精英策略,大大增强了算法的高效性和收敛性。最后的仿真结果表明,该算法可靠有效,对解决火力分配问题具有一定的实际意义。