基于机器学习的联合作战任务筹划模型

王续涵,陶九阳,吴 琳

(国防大学联合作战学院,北京 100091)

作战任务筹划(Mission Planning)是指挥员和指挥机关以战场态势为依据,针对作战任务进行的一系列有序运筹设计,是最重要的作战活动之一。作战任务筹划有两个基本问题:第一,针对一个特定作战任务,如何分配有限的作战资源;第二,针对一系列作战任务,如何确定任务执行的先后顺序[1]。

用于任务筹划的理论方法不断涌现,传统的方法主要有数学规划方法,包括整数规划、线性规划、动态规划以及多目标规划等;基于多Agent的仿真;启发式方法,包括遗传算法、粒子群算法、蚁群算法等,分布式马尔科夫决策方法等[2-3]。上述方法多用于特定作战领域或战术行动,如无人机任务航迹规划[4-5]、传感器资源的任务规划等[6-7]。针对规模较大的联合作战任务筹划问题,目前主要以定性描述为主,如美军和北约的基于重心的联合筹划概念模型,定量计算方法公开文献鲜有报道。传统方法主要用战场侦察数据、规则来进行推理和求解,不具备自学习应对战场不确定性的能力。

近年来,机器学习技术的快速发展,涌现出一批解决复杂筹划问题的新技术和新方法,为解决上述问题提供了新思路。2020年,DeepMind发布的Muzero[8]通过基于融合表征网络的自博弈方法在围棋、将棋和国际象棋等30多款雅达利游戏中“无师自通”,展现了超越人类的规划与可塑性。DeepStack采用递归推理和深度学习[9],“冷扑大师”(Libratus)采用了蒙特卡洛嵌套子博弈求解方法[10],在德州扑克不完美信息博弈中独领风骚,而且能够有效应对“咋呼”等欺骗策略;空战飞行员ALPHA AI[11]采用了遗传模糊树技术,成为最接近实际战争的人工智能;OpenAI Five[12]、AlphaStar[13]、JueWu在环境复杂、不完美信息的RTS游戏中战胜了大部分人类玩家。虽然上述人工智能都在特定领域击败了人类,展示了机器学习技术在筹划和推理方面的强大能力,但依然难以直接用于联合作战任务筹划建模。

上述人工智能技术虽然迥异,但也具备共同点:一是基于对战平台的自博弈,二是多种智能技术集成学习。借鉴上述人工智能技术成功经验,本文面向作战任务筹划的两个基本问题,首先提出了任务矩阵概念模型,为联合作战任务筹划提供了框架;以此为基础,建立了“作战任务-作战要素”关联关系的信念网络模型,提出了一种基于想象力加速的贝叶斯学习算法,通过自博弈来学习信念网络模型的参数,解决联合作战任务筹划中的资源分配问题;以学习得到的参数为基础,提出了深度最小威胁生成树搜索算法,解决任务执行的先后顺序。本文的研究旨在为指挥员和筹划人员提供理论方法和技术手段,同时也可为联合作战智能对抗仿真建模提供任务规划算法。

1 基于想象力机制的作战资源分配贝叶斯学习模型

本节构建任务矩阵模型对战场态势进行建模,使用信念网络模型刻画任务矩阵中各要素间的复杂关系,并将想象力机制融入贝叶斯方法对参数进行学习,基于参数给出任务执行中关键的支撑要素与威胁要素。

1.1 任务矩阵模型

联合作战指挥员在确定或受领作战任务后,首先需要明确任务目标和限制条件。指挥员进行作战筹划需要关注的战场态势要素通常有三种:第一种是能够提供任务完成所需资源和能力的己方要素,称为支撑要素,解决指挥员“什么可以用”的问题;第二种是能够威胁任务完成的敌方作战力量或环境要素,称为威胁要素,表明了执行任务“面临哪些威胁或阻力”;第三种,与任务执行相关的重要事件,通常是任务分析和筹划过程中需要预先设想的事件,或任务执行过程中已经发生的事件,称为任务事件,充当指挥员的“任务监视器”。任务事件的发生,往往标志任务需要调整、取消、终止、结束等。将作战任务-支撑要素-威胁要素-任务事件按照矩阵的方式组织起来,就得到了如表1所示的作战任务矩阵模型,其可以为指挥员和筹划人员提供一种分析工具。

表1 作战任务矩阵模型Tab.1 Joint operational task matrix

在高度动态联合作战背景下,海量支撑要素与威胁要素分布于陆、海、空、天、电、网等各个作战域。指挥员或筹划人员如果对每一个要素都进行深入分析,必然无法跟上战争的节奏。因此,需要一种自动化的处理方法,从海量的作战要素中确定关键的支撑要素与威胁要素,作为下一步作战资源分配的依据。为此,本文建立一种信念网络模型(也称为有向概率图),实现对所有的支撑要素和威胁要素进行重要度排序。

1.2 作战任务矩阵的信念网络模型

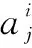
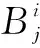
图1 作战任务-作战支撑-作战威胁的信念网络模型Fig.1 The element in TM model

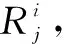
(1)

(2)

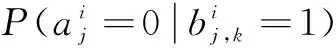
(3)

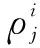
1.3 基于想象力机制的贝叶斯学习参数估计模型

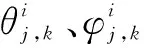
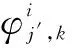
(4)

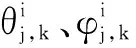
表2 算法1:基于想象力加速的参数学习算法Tab.2 Algorithm1: parameter learning algorithm based on imagination acceleration

区别于DeepMind想象力模型解决纵向想象(想象同一个对象的后续动作),本文中使用的想象力机制是横向想象,即想象其他不同对象在遇到相同情况会怎样,更适合求解样本稀疏的广度学习问题。

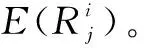
(5)

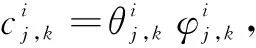
(6)

基于以上排序,可以得出执行任务mi时的关键支撑要素与si执行任务mi时的关键威胁要素。

2 基于深度最小威胁生成树搜索的任务优先级模型

作战筹划人员在面临多个任务时,需要确定任务的优先执行顺序。在任务执行的过程中,先执行的任务会对后续的战场态势要素产生影响,因此任务执行的顺序不同,完成所有任务的战损和代价往往也不同。假设完成所有任务获得的总收益相同(如果没有该假设,将变为一个更复杂的多目标动态决策问题。实际作战中该假设通常成立)。任务排序问题可以描述为以下动态规划模型:

(7)

公式(7)所示动态规划模型的优化目标是通过优化任务执行顺序,使完成所有任务的总损耗和代价最小。约束条件为每一个任务Ti都完成,总任务时间不能超时,并且每一个任务面临的威胁ci非负。

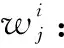
(8)

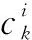
(9)

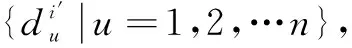
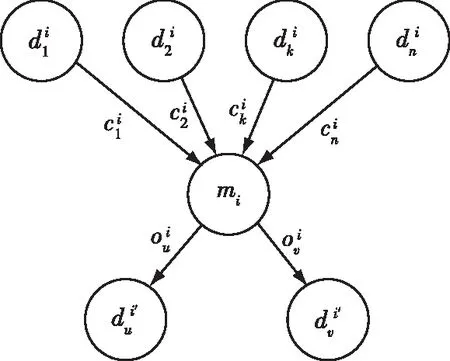
图2 单任务威胁树Fig.2 Threat tree of single task

由此,可以将公式(7)所示的动态规划模型等价于求解一个最小威胁树。一种最为直接的方法就是将所有的树全部排列一遍,时间复杂度为O(n!),在有较多的任务需要排列时,时间耗费巨大,无法满足作战时效性要求。因此,本文设计一种深度优先最小威胁生成树搜索算法,通过均衡搜索误差和速度实现任务优先级排序,如表3所示。

表3 算法2:深度优先最小威胁生成树搜索算法Tab.3 Algorithm2: depth first minimum threat spanning tree search algorithm

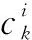
3 仿真实验验证

本文以一次火力打击与防御作战为仿真案例,检验上述模型和算法的有效性。首先设置初始仿真实验条件,对模型中需要的参数进行初始设定;然后通过多次推演来分析上述模型的学习能力和计算结果。

3.1 实验环境的设置

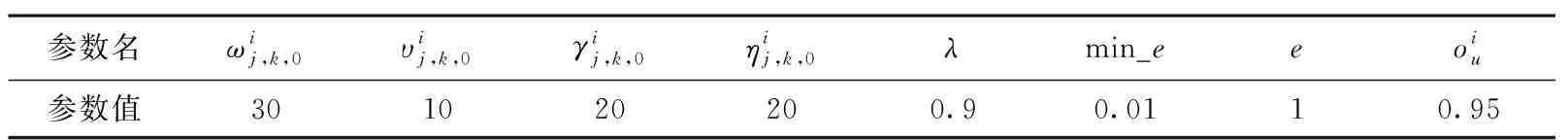
表4 算法初始化参数Tab.4 Initial parameters of the algorithm

在执行任务过程中,红方每个支撑要素被蓝方要素的毁伤概率在[0,1]区间随机生成。生成的毁伤概率表只为仿真实验提供交互结果计算,毁伤概率表对红方不可见。

3.2 仿真结果分析

以上述初始参数为基础,在仿真推演过程中,算法1和算法2的计算结果可以通过图4所示的示意图表示。

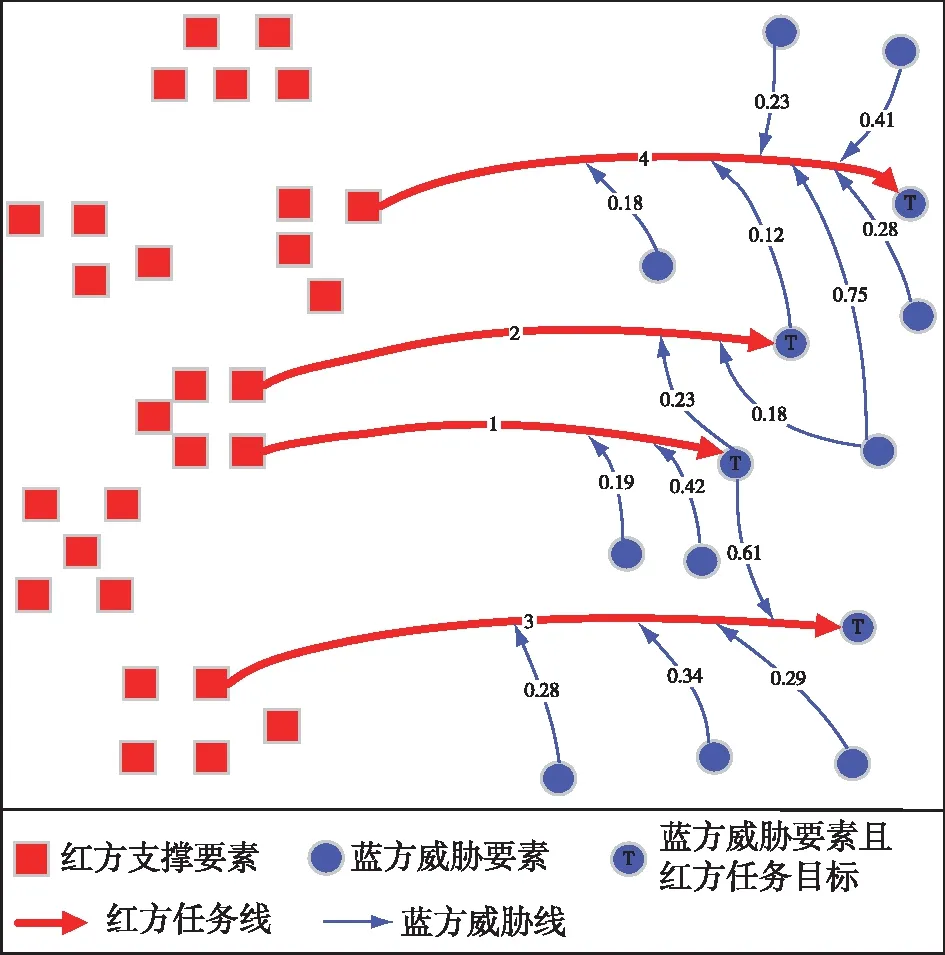
图4 算法计算过程示意图Fig.4 Diagram of the calculation process

在任意时刻,由算法1的计算结果可以确定红方任务线和蓝方的威胁线,任务线是指从某个支撑要素到某个任务目标之间的连线,威胁线是指从威胁要素到任务线某点的连线。算法1同时确定了关键支撑要素和关键威胁要素,分别为任务线的起点和威胁线的起点。算法2确定了任务的优先顺序,如图4所示,四个任务的执行顺序从上到下排列为4-2-1-3。

参数学习算法和深度优先最小威胁生成树搜索算法的有效性,可以通过红方完成所有任务后支撑要素的损失数目来检验。由于作战过程具有随机性,例如,一枚导弹可能击中目标也可能没有击中目标,这种不确定性对于战争结果的影响可能非常大,对应到本文的仿真实验就是会导致仿真实验结果具有较大波动性。因此,为了尽可能地消除这种不利影响,我们对每一个学习出来的参数运行10次,并对结果取平均值。得到如图5所示的结果。

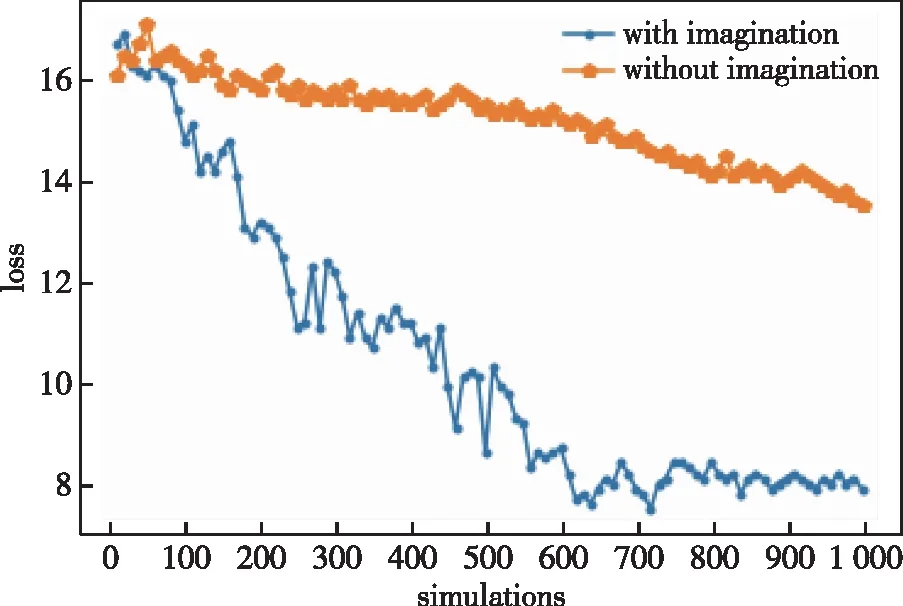
图5 红方执行任务损失支撑要素数目情况Fig.5 Number of supporting elements for red party’s loss in task execution

共进行了1 000次仿真实验,纵坐标表示红方支撑要素的损失数目。蓝色曲线和黄色曲线分别表示采用和未采用上文提出的想象力机制模型的学习情况。通过对比可以发现,采用想象力机制能够使模型收敛速度大大加快。当需要学习的参数随着态势要素数目一起增多,先验知识将会变得更加稀疏,带有想象力机制的学习模型收敛速度优势会更加明显。但也要看到,蓝色曲线在收敛过程中震荡较大,原因可能是很多参数的更新建立在想象而非真实体验之上。

4 结束语

本文提出了一种基于机器学习的任务资源分配和任务优先级排序方法,通过想象力机制加速了学习模型的收敛速度,仿真实验表明了该方法的有效性。该方法不仅能够为指挥员和联合筹划人员提供有益的分析工具,同时也可以为作战博弈系统提供智能学习算法。由于战争问题的极端复杂性,为了建模方便,本文提出的方法对很多问题进行了简化,所用方法也比较简洁,旨在探索理论方法和技术路线。本文下一步的工作是更为深入地讨论并行任务的搜索、任务协同等问题。