追根溯源,深化理解
桑坤



摘要:调查发现,“简便”是学生对竖式运算顺序的主要认知依据。对此,教师带领学生展开一场对“竖式”追根溯源的探寻,借助相关史料,引导学生在不断地“猜想—验证”中,明了竖式的“前世今生”,深化对竖式的理解。
关键词:小学数学;竖式;数学史料;质疑精神
一、教學背景
三年级教学“两、三位数除以一位数”时,有学生会问:在用竖式计算加法、减法、乘法的时候都是从低位算起,为什么在用竖式计算除法的时候就要从高位算起?除法竖式是否也能从低位算起?受到之前学习的加法、减法和乘法竖式计算经验的负迁移,学生产生这样的疑惑是非常自然的。这个问题也具有
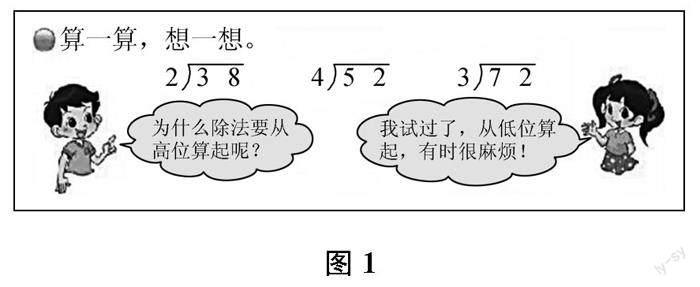
研究的意义和价值。笔者翻阅了各个版本小学数学教材后发现,只有北师大版小学数学三年级下册《除法》单元中对这一问题有所提及(见图1),但并未作出详细的解释与说明。图中女孩的回答仅仅是:“从低位算起,有时很麻烦!”但“麻烦”并不意味着不能从低位算起。
鉴于此,笔者在所执教的六年级一个班做了一次“关于‘竖式’,你知道多少?”的学情调查,想了解一下即将毕业的小学生对于“竖式”知道些什么、思考过什么、是否产生过质疑。具体调查内容如下:(1)在用竖式计算乘法的时候,我们是从低位算起,是否也可以从高位算起?你是怎么想的?试着将你的想法写出来。(2)在用竖式计算加法、减法和乘法的时候,我们是从低位算起,为什么除法竖式却从高位算起?是否也可以从低位算起?你是怎么想的?试着将你的想法写出来。
关于问题1,所有学生都认为可以从高位算起,但基本上都认为从高位算起比较麻烦(图2所示即为一名学生的回答)。关于问题2,64%的学生认为可以从低位算起,同样认为从低位算起比较麻烦;36%的学生认为不可以从低位算起(图3所示即为一名学生的回答)。
从调查的结果来看,“是否简便”是学生对竖式运算顺序的
主要认知依据。而对于竖式的书写格式,以及竖式的运算顺序等规定的缘由,学生没有做过多思考,属于“接受型学习”。即使有一些疑惑,
可能也在教师“就是这样规定的”“从来如此”等简单粗暴的解释下,被按回了心里。这无疑扼杀了学生的创造性,限制了学生探究能力的发展。
如何抓住学生的质疑,让他们对“竖式”的相关内容有更为深入的了解?笔者认为,可以带领学生展开一场对“竖式”追根溯源的探寻,借助相关史料,引导学生在不断地“猜想—验证”中,明了竖式的“前世今生”,深化对竖式的理解。
二、教学过程
(一)问题引领,自主探寻揭本质
1.问题引领,聚焦本质
师同学们,今天我们一起研究的关键词是——竖式。
关于“竖式”,你们都知道些什么呢?
生我们已经学习了加法、减法、乘法和除法竖式。
生我们学习的竖式中,有整数和小数的竖式。
生用竖式计算加法、减法、乘法的时候,都是从低位算起的。
生用竖式计算除法的时候,是从高位算起的。
师对于我们一直在用的竖式,你是否产生过一些疑惑?
生在用竖式计算加法、减法、乘法的时候都是从低位算起,为什么在用竖式计算除法的时候就要从高位算起呢?
生除法竖式是否也能从低位算起?
师为你们善于思考、敢于质疑的学习品质点赞
。今天这节课,我们就围绕这两个问题,开启我们的探索之旅。
2.合作交流,探寻本质
师对于“除法竖式为什么要从高位算起?”“除法竖式是否也能从低位算起?”这两个问题,大家有什么想法?四人小组交流,将你们的思考过程写下来。
(学生交流、汇报。)
生我们小组交流后的思考是这样的:竖式计算除法的时候是可以从低位算起的,(展示做法,如下页图4所示)以58÷2这道除法竖式为例,但计算的过程会比较麻烦,步骤比较多。
生我们同意第一小组的想法,如果是三位数除以一位数的竖式,步骤会更多、更麻烦。
生我们还可以借助小棒来理解。例如,(展示做法,如图5、图6所示)在列竖式计算32÷2时,先分十位,再分个位只需要平均分2次;而从个位分起,需要平均分3次。
师我们在研究问题的时候,都是从简单到复杂的。之前,大家举的例子都是能够整除、没有剩余的情况,那不能整除、有剩余的情况是否也一样呢?大家试着再举例说明。
(学生讨论、汇报。)
师我们通过举例子、摆小棒,用自己的方法对除法竖式的计算顺序进行了分析与说明。大家明确了两点:(1)竖式计算除法的时候是可以从低位算起的;(2)从低位算起会比较麻烦,步骤较多。这是同学们共同思考的成果,为大家点赞。
(二)回顾历史,追溯除法竖式的根源
师通过自主探究,同学们清楚地认识到用竖式计算除法从高位算起的缘由。可是,对于即将小学毕业的你们,仅仅知道这些
是远远不够的,我们需要进一步探寻除法竖式背后的故事。除法竖式是如何演变成现在的样子的?接下来,我们就一起走进数学历史的长河中去一探究竟。历史上出现过许多看起来极其烦琐的除法竖式计算方法。
(出示图7)我们先来看清代《御制数理精蕴》一书中介绍的一种极具特色的除法计算方法。原书中对计算过程的描述为:“法以六十四石为实列于下,八人为法列于上,因法之八大于实之首位之六,故将法退一位书之。再看实足法几倍,今足八倍,故书八于法上。乃以得数之八与法之八相因得六十四书于实下,与实相减恰尽,得数为八石也。”请结合这个竖式和这段文字,同桌互相说一说这个除法竖式的计算过程。
(学生同桌交流。)
师(出示下页图8)这一计算过程可以用现在的语言结合图示作出解释。第一步,把被除数“64”写在下面,除数“8”写在上面。因为除数“8”大于被除数最高位上的“6”,所以要退一位写。这实际上是运用乘法计算除法,相当于思考“8乘以多少等于64”。第二步,看被除数最多包含除数的几倍,可以看出最多包含8倍,所以在除数上面写“8”。第三步,将得数“8”与除数“8”相乘得“64”,写在被除数“64”的下面。第四步,与被除数相减,恰好得“0”。说明得数就是“8”。这种竖式书写格式和我们现在什么计算的格式比较像?
生像乘法的竖式。
师确实,它是在利用乘法竖式的写法来计算除法。这本书中对于比较复杂的除法也采用了同样的计算方法,(出示图9)如9225÷45。同桌互相说一说被除数、除数、商在哪?
生其中的“九二二五”是被除数“9225”,“四五”是除数“45”,上面的“二〇五”是商“205”。
师谁还有补充?
生把竖式中的除数“四五”移到左侧,加上“丿”,就和我们现在所写的除法竖式很接近了。
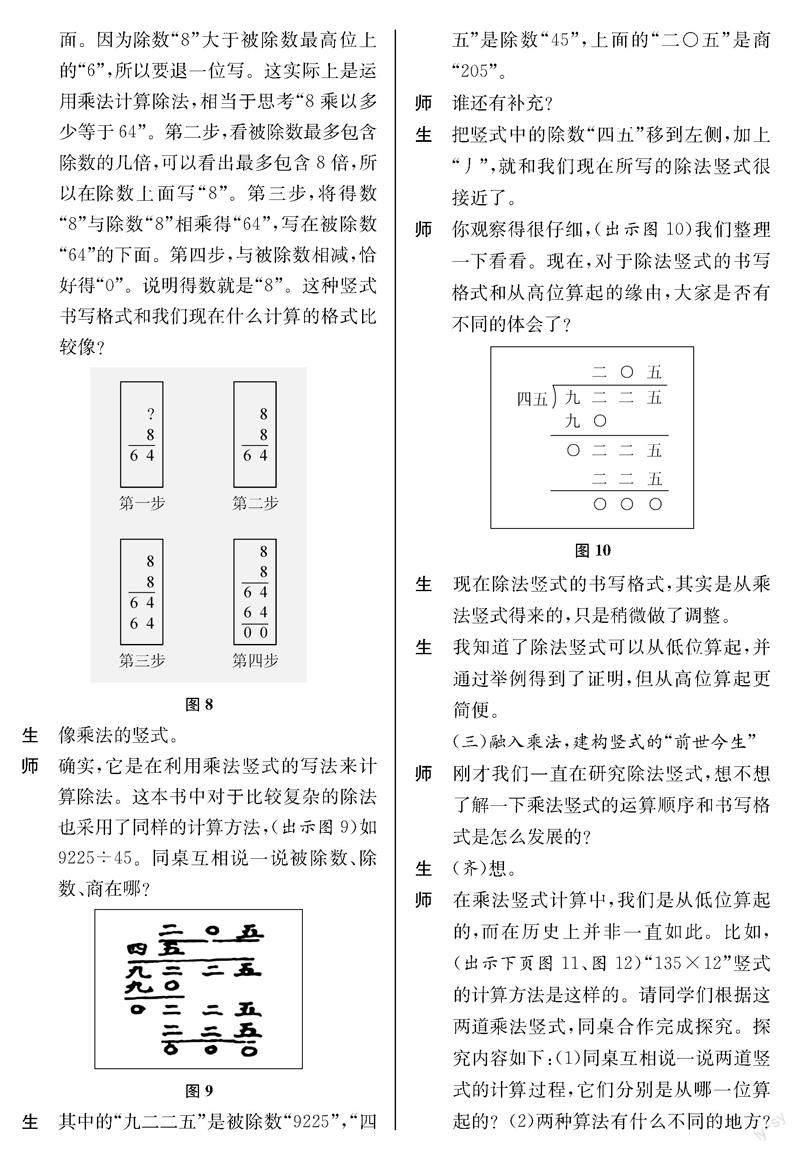
师你观察得很仔细,(出示图10)我们整理一下看看。现在,对于除法竖式的书写格式和从高位算起的缘由,大家是否有不同的体会了?
生现在除法竖式的书写格式,其实是从乘法竖式得来的,只是稍
微做了调整。
生我知道了除法竖式可以从低位算起,并通过举例得到了证明,但从高位算起更简便。
(三)融入乘法,建构竖式的“前世今生”
师刚才我们一直在研究除法竖式,想不想了解一下乘法竖式的运算顺序和书写格式是怎么发展的?
生(齐)想。
师在乘法竖式计算中,我们是从低位算起的,而在历史上并非一直如此。比如,(出示下页图11、图12)“135×12”竖式的计算方法是这样的。
请同学们根据这两道乘法竖式,同桌合作完成探究。探究内容如下:(1)同桌互相说一说两道竖式的计算过程,它们分别是从哪一位算起的?(2)两种算法有什么不同的地方?(3)比较现在乘法竖式的计算过程,你有什么想说的?
生左边的竖式是将135分成“100+30+5”,分别和12相乘来计算的;右边的竖式是将12分成“10+2”,分别和135相乘来计算的,都是从高位算起的。
师说得真好!从历史上的算法来看,我们现在所规定的从“从低位算起”并不是唯一的。从计算的过程和步骤中,我们能体会到“从低位算起”书写的简约与
方便。同学们,今天我们一起探寻了乘法、除法竖式的“前世今生”,从历史的视角探寻了竖式的演变过程。希望通过这节课的学习,你们对“竖式”
能有更多不一样的认识。最后,我们能否大胆猜测一下:在若干年后,竖式是否还会发生变化?会发生怎样的变化?
三、教学思考
对于数学规定,如果教师按部就班地施教、学生不假思索地接受,这些约定成俗、理所应当的规定就如水中的浮萍,容易导致学生“一学就懂,一做就错”。因此,教师需要
引导学生把目光聚焦于数学规定背后所隐藏的思考过程。“数学是积累的科学,它本身就是历史的记录。或者说,数学的过去融合在现在与未来之中。”[1]以“史”化人的理念给当下的数学课堂注入了新的能量。将数学知识背后所蕴含的数学思想、数学精神、数学史等相关
内容与数学知识进行联结,能让学生在感受数学理趣的同时,厘清数学知识的来龙去脉,并深化理解。
本课中,笔者先呈现了数学史料中除法的竖式格式及其计算过程,让学生初步感受古代的除法竖式与现在的乘法竖式很像。然后,引导学生带着这样的感受,一步一步地揭开除法竖式的秘密,从而让学生对“除法竖式为什么从高位算起?”这一问题有更为清晰且深刻的理解。紧接着,笔者顺势引出乘法竖式的相关数学史料,让学生在小组交流与合作中继续思考。
六年级学生有能力自主探究竖式的“前世今生”,体会与感悟现在的竖式与过去的竖式的异同,从根本意义上理解我们所认为的“约定俗成”“简便”的深层含义。在演算、证明的过程中,学生提升了分析问题、解决问题的能力;在回顾历史、审视计算方法的过程中,学生深化了对知识的理解。
当然,数学史料的使用不是简单的呈现,而应融入具体的教学情境中。具体地,笔者创设了两处认知冲突,助力学生的探究学习,同时培养学生的质疑精神。其一,除法竖式通常从高位算起,是否也能从低位算起?其二,乘法竖式通常从低位算起,是否也能从高位算起?调查发现,学生目前的認知仅停留在除法竖式从高位算起、乘法竖式从低位算起的简单理解层面。这样的两处认知冲突,从儿童的认知视角出发,翻转约定俗成,在充分体现知识之间的密切联系的同时,激发学生自主探究的意识,引领学生积极、主动地参与探究活动,并在探究活动中更好地感悟数学的理性与严谨,更好地理解数学知识的内涵与外延。
参考文献:
[1] 郜舒竹.小学数学这样教(第2版)[M].上海:华东师范大学出版社,2021:6469.

