700 MPa级高强钢层流冷却过程的多场耦合数值模拟

吕 博 刘 锟,2 李晓林,2 梁江涛 魏绍东 肖宝亮,2

(1.首钢技术研究院,北京 100043; 2.绿色可循环钢铁流程北京市重点实验室,北京 100043)

700 MPa级高强钢具有高强度、高塑性以及良好的焊接性能,被广泛应用于汽车、工程机械等领域。其生产流程包括炼铁、炼钢、连铸、粗轧、精轧、层流冷却、卷取等工序,其中层流冷却过程能够控制带钢的板形、微观组织以及温度场分布,是复杂的温度场、相变场以及应力应变场耦合问题。

目前,有较多的学者研究了热轧带钢在层流冷却过程中的多场耦合仿真。Tian等[1]提出了一种计算层流冷却换热系数的方法,得到了以喷嘴为中心的半正弦波和直线组成的分段函数的传热系数分布形式。邱增帅等[2]通过仿真模拟计算,基于密集冷却工艺建立了层流冷却耦合模型,提出了减小700 MPa级高强钢残余应力的方法。孙明军等[3]建立了带钢船形冷却的温度-相变耦合模型,以JMAK方程为相变动力学方程,采用六次高斯曲线进行船形冷却效率拟合,根据模拟结果优化了生产工艺。王乙法等[4]建立了X70钢层流冷却过程的热-力-相变耦合模型,研究了温度、组织、应力和应变的不均匀分布规律,提出了使用边部遮蔽的方法减小带钢残余应力。Xu等[5]通过搭建实验平台,测量了距钢板上表面1 mm时在基体层流喷雾冷却过程中钢板的传热特性,并采用时间序列函数法计算了钢板表面温度和综合传热系数。

本文通过建立带钢二维有限元模型,对层流冷却过程进行了多物理场耦合仿真,并联合子程序计算了带钢的相变效应,得到了较为准确的结果。通过设置合适的边部遮蔽宽度,可以改善带钢边部的残余应力状态,使板形得到改善,为实际生产过程中的工艺调整提供指导。

1 有限元模型的建立

1.1 几何模型及网格划分

为便于研究,根据带钢在层流冷却过程中的换热特点,对模型进行如下简化[6-7]:

1)忽略带钢沿轧制方向的换热;

2)忽略带钢轧制速度波动对带钢表面对流换热系数的影响。

建立带钢横断面全尺寸的二维几何模型,示意图如图1所示,模型尺寸为1 250 mm×3 mm。

图1 带钢横断面二维几何模型示意图Fig.1 Schematic diagram of two-dimensional geometric model of cross section of the strip

带钢在层流冷却过程中主要是通过上下表面与空气和冷却水进行换热,并且带钢边部受冷却水流动的影响,温降较快。因此对模型进行网格划分时,将模型上下表面以及边部的网格进行加密,单元类型为四结点热力耦合平面应变四边形单元,模型边部网格划分如图2所示。

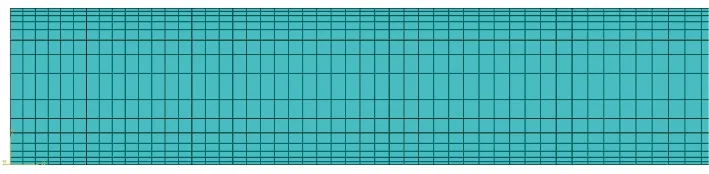
图2 模型边部网格划分Fig.2 Mesh generation of the model edge

1.2 材料属性及边界条件

试验材料为700 MPa级Nb-Ti复合高强钢,其部分物性参数受温度的影响较大[8],具体如表1所示。

表1 材料物性参数与温度的关系Table 1 Relationship between physical parameters of material and temperature

热轧带钢的层流冷却过程可以看作是有内热源的非稳态热传导过程。假设带钢相变释放的潜热在单位时间、单位体积内产生的热量为q,则带钢的二维非稳态导热微分方程为[9]:

(1)

式中:ρ为带钢密度,kg/m3;c为带钢比热容,J/(kg·℃);λ为带钢导热系数,W/(m·℃);T为带钢温度,℃;t为时间,s;q为带钢内热源生热速率,J/s。

为了简化模型并结合现场实测温度曲线,设定带钢终轧温度在宽度方向上的分布如图3所示,在厚度方向上均匀分布。

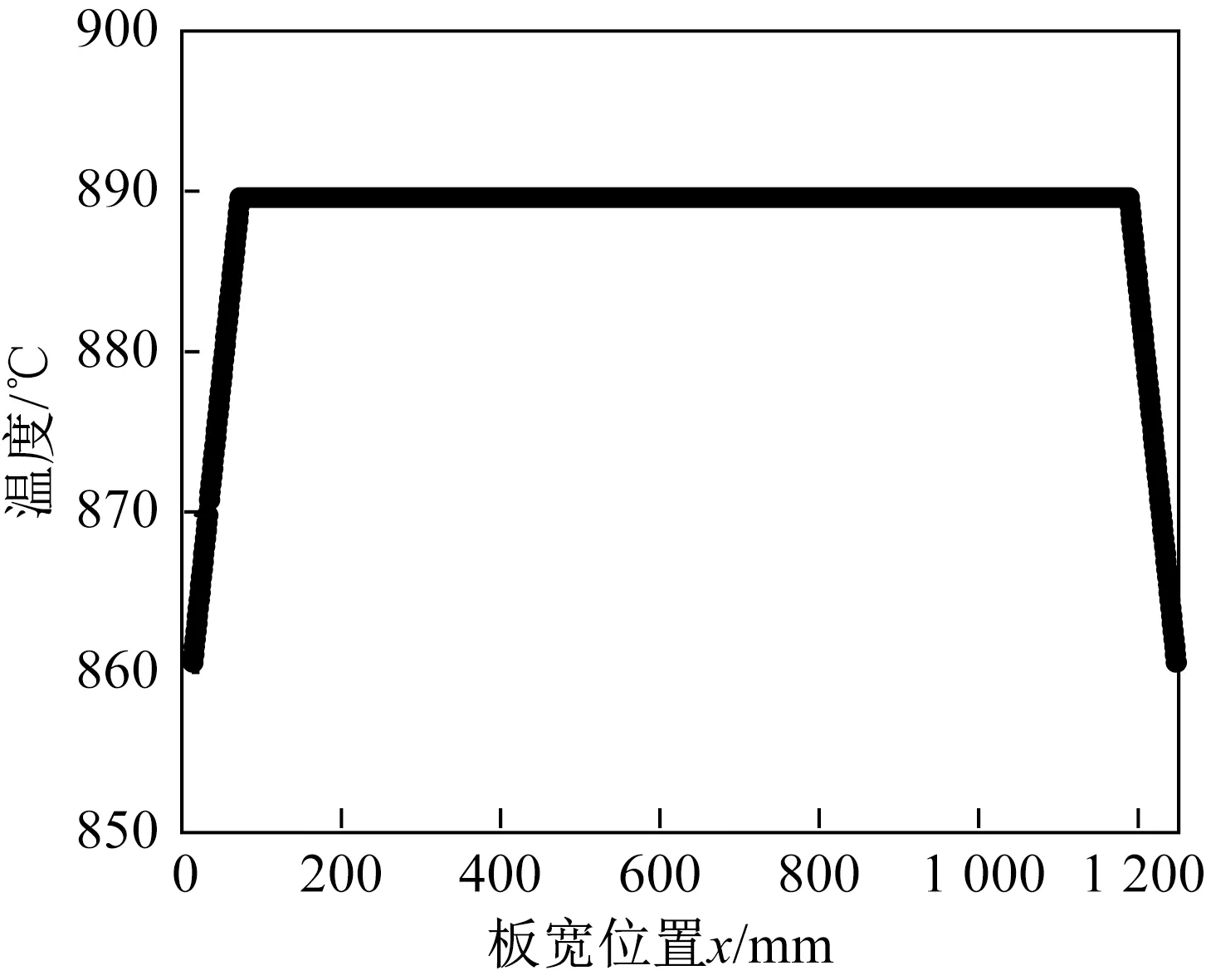
图3 带钢终轧温度在宽度方向上的分布Fig.3 Distribution of finish rolling temperature of the strip in width direction

带钢边界与环境换热符合第三类边界条件,即带钢和冷却介质温度已知,带钢和冷却介质间的换热系数可通过计算求得。因此带钢在层流冷却过程中的边界条件为[10-11]:

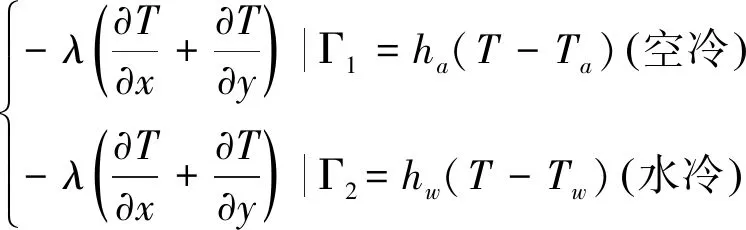
(2)

式中:Γ1表示空冷换热边界(钢板上下表面和左右两侧表面);Γ2表示水冷换热边界(钢板上下表面);ha为综合空冷换热系数,W/(m2·℃);hw为水冷换热系数,W/(m2·℃);Ta为空气温度,℃;Tw为冷却水温度,℃。

1.3 换热系数

700 MPa级高强钢的层流冷却过程可以分为5个阶段:带钢在精轧终轧结束后首先空冷(3.89 s),之后进入前段集中冷却阶段水冷(1.55 s),然后空冷(6.74 s),接着进入后段精调冷却阶段水冷(0.35 s),最后空冷(4.1 s)。带钢在空冷过程中的换热方式包括带钢与辊道之间的接触换热、带钢与空气的对流换热以及带钢表面的辐射换热,其中辐射换热为主要的换热方式,其余两种换热方式热量损失较小。为便于计算,将这3种换热方式用一个综合空冷换热系数表示[12]:

(3)

式中:ε为带钢表面辐射率,考虑到带钢与辊道接触以及与空气对流换热,取0.88;σ0为斯蒂芬-玻耳兹曼常数。

带钢在水冷过程中的换热方式为带钢上下表面和冷却水之间的对流换热,换热系数与水流密度、带钢表面温度、冷却水温度以及冷却集管布置相关,计算公式为[12]:

(4)

式中:ω为水流密度,m3/(min·m2);Pl为轧制方向喷嘴间距,m;Pc为板宽方向喷嘴间距,m;D为喷嘴直径,m。

带钢上表面冷却水的流动特性导致其边部的冷却速率大于中部,因此将上表面的水冷换热系数与板宽位置相结合,改写式(4)为:

(5)

式中:x为板宽方向与带钢对称中心的距离,m;W为带钢宽度,m。

2 相变效应

2.1 相变动力学

热轧带钢在层流冷却过程中发生相变,从奥氏体转变为铁素体和少量珠光体,产生相变效应,由于珠光体数量较少,因此忽略珠光体对模型的影响。在计算相变膨胀以及相变潜热时,需要先计算得到新相体积分数。假设新相的形核发生在奥氏体晶界,奥氏体的等温转变过程可用Avrami方程表达[4,8]:

X=1-exp(-ktn)

(6)

式中:X为新相的等温相变体积分数;t为奥氏体相变开始后的时间。

根据相变理论以及Scheil叠加法则,可以将连续冷却过程离散为多个等温转变过程,因此可以通过Avrami方程建立奥氏体转变为铁素体的连续冷却相变数学模型,式(6)中,k、n根据700 MPa级高强钢的等温转变曲线和式(7)确定:

(7)

式中:X1、X2为相同温度T下不同的转变量;t1、t2为不同转变量对应的时间。

使用Gleeble-3500热模拟试验机将700 MPa级高强钢的圆棒试样加热至960 ℃保温5 min,之后以100 ℃/s的速率冷却至目标温度(720、700、680、660、640、620、600、580、560 ℃)保温3 min,最后快速冷却至室温。图4为保温温度为720 ℃的温度-时间-膨胀曲线。

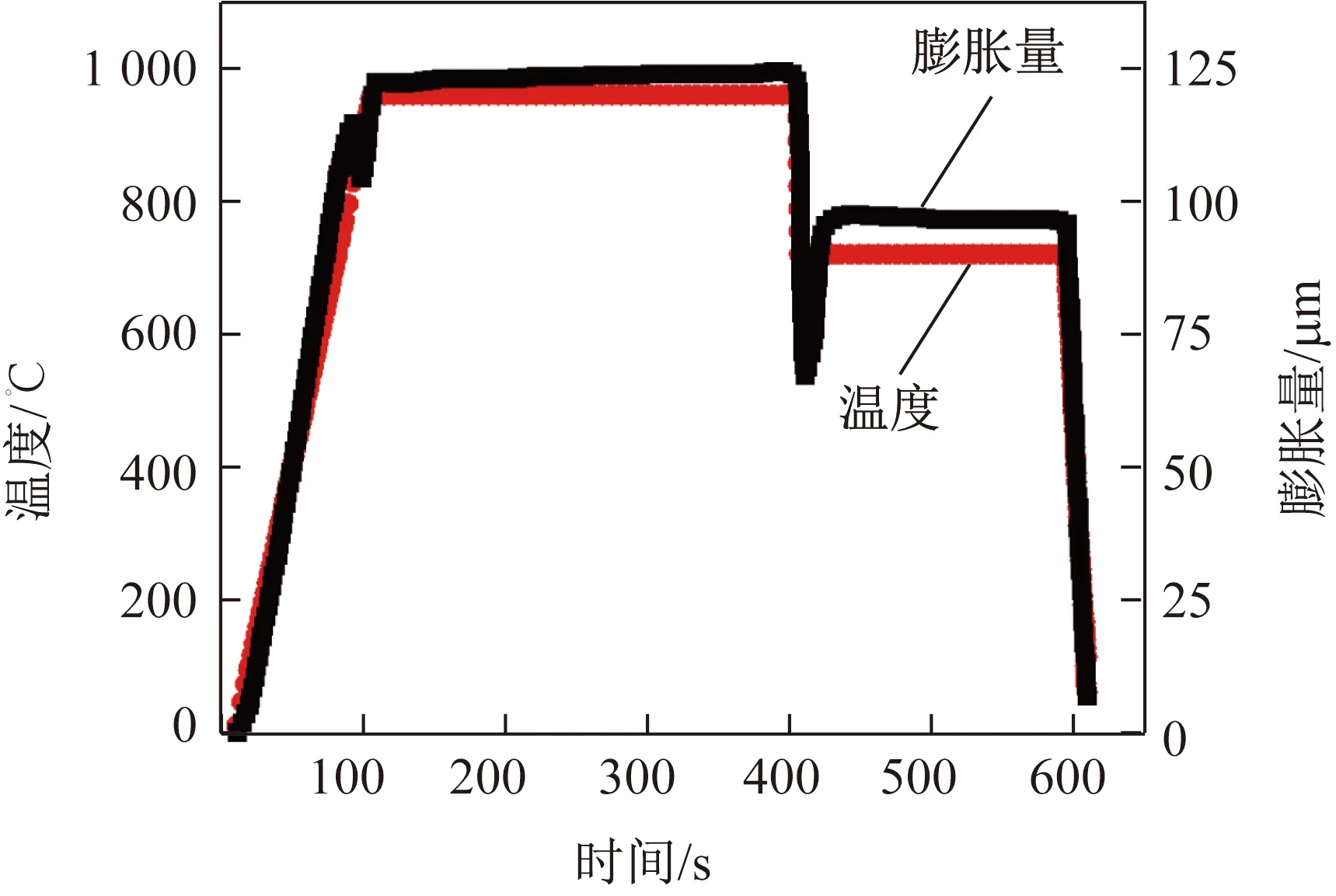
图4 720 ℃的温度-时间-膨胀曲线Fig.4 Temperature-time-expansion curves at 720 ℃

2.2 相变膨胀

由于奥氏体与铁素体的晶格存在较大的差异,因此在奥氏体向铁素体转变的过程中伴有剧烈的体积膨胀,不同的相变程度将产生不同的体积膨胀,从而造成不同的内应力分布。由相变产生的体积膨胀与材料的本征应变εtv的体积分量δ相关[12]:

(8)

式中:εtv为相变膨胀应变;I为单位张量;δ为奥氏体与铁素体的相对体积比。

2.3 相变潜热

奥氏体-铁素体相变属于“一级相变”,不仅体积会发生变化,还会释放大量的相变潜热,该热量将直接影响带钢的温度,并间接影响带钢的相变动力学、应力和应变。相变潜热可用焓差法模型进行计算[12]:

(9)

式中:qtrans为相变潜热,J/kg;HA→F为相变焓,J/kg;ρ为密度,kg/m3。试验测得奥氏体转变为铁素体的热焓值为590 MJ/m3。

上述3种计算相变效应的理论模型并不能在ABAQUS软件中直接进行求解,需要开发相应的子程序完成计算:USDFLD子程序计算相变动力学;UEXPAN子程序计算相变膨胀;HETVAL子程序计算相变潜热。在有限元模型计算的过程中,通过调用子程序完成相变效应的理论计算。

3 结果分析与讨论

3.1 温度场

为研究相变效应对带钢温度场的影响,分别建立了考虑相变效应的模型一以及未考虑相变效应的模型二。通过使用有限元仿真软件并结合相变子程序,计算得到了带钢在层流冷却过程中板宽中部上表面和心部的温度随时间的变化曲线,如图5所示。

图5 带钢上表面和心部温度随时间的变化Fig.5 Variation of temperature at upper surface and core of the strip steel with time

由图5(a)可知,带钢在空冷过程中心部和上表面温差较小,两处冷速几乎相等。在水冷过程中上表面直接与冷却水接触进行对流换热,而心部则是通过热传导的方式在带钢内部进行传热,因此带钢心部温度会短暂地高于表面温度,但水冷结束后带钢上表面迅速返温,内部导热大于表面换热,心部温度和上表面温度趋于一致,最终卷取温度为622 ℃。对比图5(a)和5(b)可知,若未考虑相变效应,在第一段水冷后带钢温升量明显减小且心部温度持续降低,说明在此阶段只有短暂的返温过程而没有相变潜热,与模型吻合。经过后续的冷却过程,最终卷取温度为582 ℃,相比考虑相变效应的情况低40 ℃,说明在层流冷却过程中相变潜热对带钢温度场产生了较大的影响。

使用FLIR热成像仪测得层流冷却结束时带钢尾部100 m处板宽方向的温度分布,与计算得到的温度曲线进行对比,如图6所示。

图6 带钢板宽方向实测温度曲线与模拟温度曲线对比Fig.6 Comparison between measured and simulated temperature curves in width direction of the strip steel

由图6可知,带钢板宽中部温度实测值在600～640 ℃内波动,模拟值则基本上为一条水平直线。其原因是仿真模型未考虑带钢终轧温度的波动,导致最终卷取温度模拟值与实测值产生误差,误差为3.2%,在可接受范围之内,模拟值与实测值吻合度较高。

3.2 相变场

带钢上表面和心部的新相体积分数随时间的变化如图7所示。由图7可知:在5 s左右带钢开始发生相变,由于上表面冷却速率较快,首先发生相变;在10 s左右上表面和心部的新相体积分数趋近于1,说明带钢基本完成相变。

图7 带钢上表面和心部新相体积分数随时间的变化Fig.7 Variation of volume fraction of new phase on upper surface and in core of the strip steel with time

3.3 残余应力

由于带钢边部冷却能力较强,且初始温度低于带钢中部,导致层流冷却后带钢边部温度较低,产生了较大的残余应力,带钢容易产生边浪。通过使用合适的边部遮蔽策略可以改善带钢边部温降,设置仿真模型边部遮蔽宽度为50、100及150 mm,通过编写FILM子程序控制带钢上表面的水冷换热系数。使用边部遮蔽后,带钢边部的水冷换热系数呈指数形式递减,板宽方向的水冷换热系数计算公式为[13-16]:

(10)

式中:x为板宽方向与带钢对称中心的距离,m;B为边部遮蔽宽度,m。

经过仿真模拟得出,层流冷却结束后,带钢边部200 mm内上表面的温度和残余应力变化分别如图8(a)和8(b)所示。随着边部遮蔽宽度的增加,带钢边部与心部的温差逐渐减小,残余应力差也不断减小。带钢边部温度从580 ℃提高至610 ℃,残余应力从203 MPa降低至170 MPa,说明合理地使用边部遮蔽策略能有效改善带钢边部温差,减小残余应力。

图8 带钢边部200 mm内上表面温度(a)与残余应力(b)的变化Fig.8 Variation of temperature(a) and residual stress(b) in upper surface within 200 mm of the strip steel edge

不同边部遮蔽宽度下带钢边部200 mm内板形的变化如图9所示。由图9可知:当边部遮蔽宽度为50 mm时,板形改善不明显,带钢边部仍存在下翘缺陷;当边部遮蔽宽度为100 mm时, 板形有了明显改善,下翘缺陷消失;当边部遮蔽宽度为150 mm时,又出现上翘缺陷。结合带钢边部温度与残余应力的变化,可以得到边部遮蔽宽度设置为100 mm较合适。

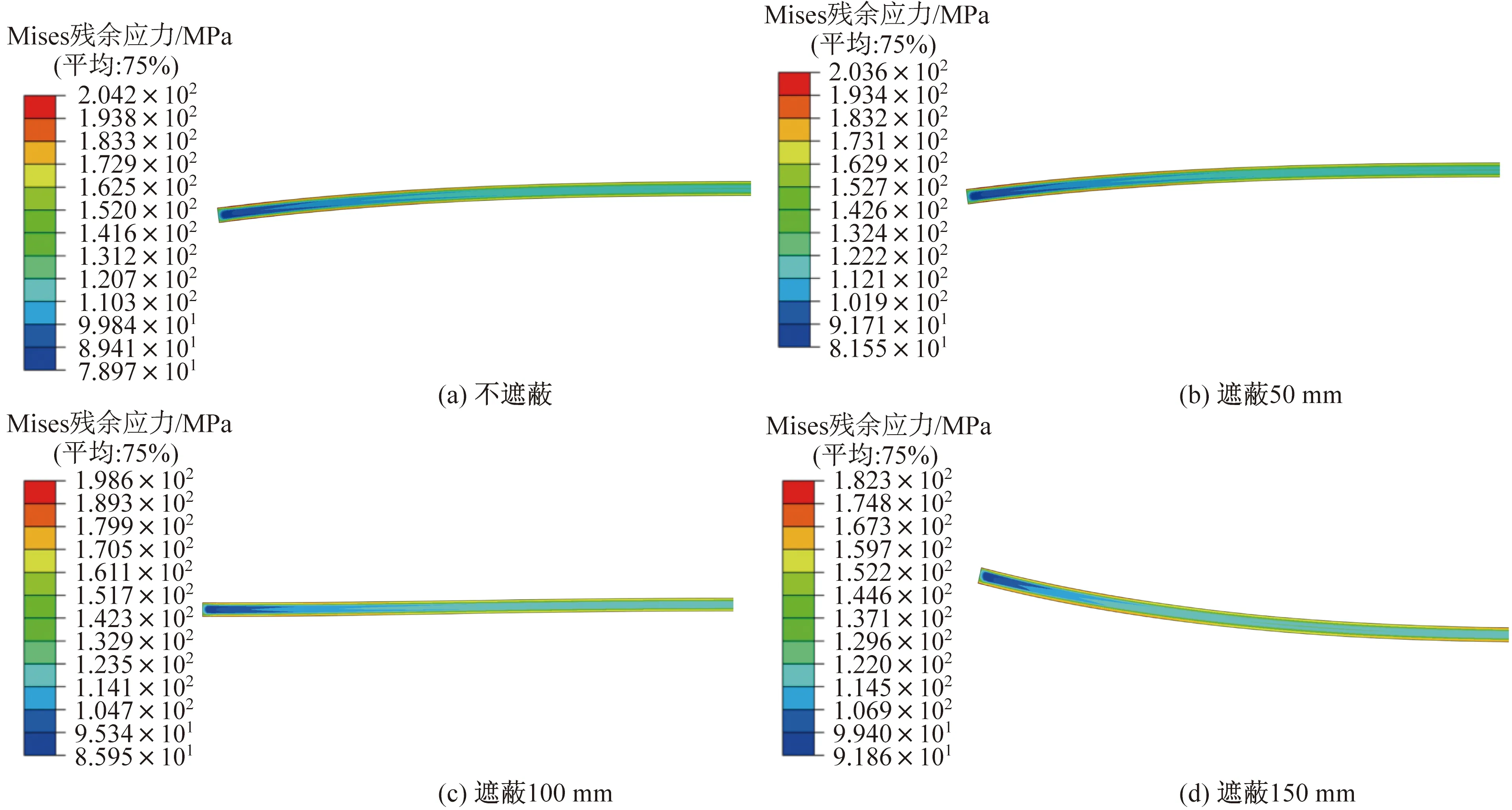
图9 边部遮蔽宽度对带钢板形的影响Fig.9 Influence of edge masking width on shape of the strip steel

4 结论

(1)带钢经过第一段水冷,温度降至650 ℃左右,但由于冷速较大未发生相变,在空冷阶段迅速发生相变,相变潜热对带钢温度场影响较大,对于该成分体系的700 MPa级高强钢,相变潜热对卷取温度的贡献约为40 ℃。

(2)带钢上表面层流冷却水的流动特性导致其边部的冷却能力高于中部,因此带钢边部温度较低,残余应力较大,并且出现了下翘缺陷。通过仿真模拟计算,在带钢层流冷却过程中使用边部遮蔽策略,能够较好地改善带钢边部缺陷,边部遮蔽宽度设置为100 mm较合适。

(3)建立的700 MPa级高强钢多场耦合仿真模型考虑了带钢在层流冷却过程中相变效应对温度场、应力应变场的影响,温度场计算结果与实测值吻合度较高,模型预测较为准确。通过调整冷却模式计算得到对应的物理场分布,能为实际生产过程中板形的控制提供一定的理论指导。