SUS304不锈钢冷轧粘辊现象的改善方法
李均禹 李立新 周 顺 彭 洲 苏 严
(武汉科技大学 省部共建耐火材料与冶金国家重点实验室,湖北 武汉 430081)
SUS304不锈钢是一种应用广泛的奥氏体不锈钢,在其冷轧生产过程中时常会发生粘辊现象。粘辊是指轧制材料的部分碎片在轧制过程中不断粘附累积在工作辊表面,导致工作辊使用寿命缩短、产品表面质量恶化。国内外学者一直在研究粘辊机制及其影响因素[1-6]。由于铁素体不锈钢的粘辊现象比奥氏体不锈钢严重得多[7],目前关于铁素体不锈钢热轧粘辊的研究较多,而对奥氏体不锈钢冷轧粘辊的研究较少。彭艳等[8]建立了冷轧粘着指数模型,并作为判断钛板冷轧粘辊程度的依据,这为判断奥氏体不锈钢冷轧粘辊程度提供了思路。
本文以SUS304奥氏体不锈钢为研究对象,在已有粘辊模型的基础上,考虑冷轧时轧辊的弹性压扁以及前后张力等影响,从轧制规程、轧制速度、轧辊尺寸等方面探究了影响粘辊的主要因素,并提出了具体改进措施。
1 粘着指数模型优化
已有的冷轧粘着指数模型[8]:
λ=f(Ea,M,Tm,ξ50,V,ε,k,p,c,H,h1,r,RZ,ΔγA-B)
(1)
式中:λ为粘着指数,其值与材料性质、润滑油性能、轧制工艺参数等有关;Ea为润滑油吸附能;M为润滑油相对分子质量;Tm为润滑油熔点;ξ50为润滑油在50 ℃时的运动黏度;V为轧辊的圆周速度;ε为压下率;k、p、c分别为轧件的热导率、密度和比热容;H为板材硬度;h1为轧件出口厚度;r为轧辊半径;RZ为轧辊表面不平度的平均高度;ΔγA-B为界面粘着能。考虑到不同材料对于模型的适用情况存在差异,为了更好地表征SUS304不锈钢在实际冷轧时的粘着程度,本文对其冷轧粘着指数模型进行了优化。
1.1 润滑油膜破裂失效的临界温度
塑性加工过程通常处于边界摩擦状态,或是以边界摩擦为主的混合摩擦状态。在边界摩擦状态,具有润滑作用的润滑剂油膜称为边界润滑膜。孙建林[9]对边界润滑膜失效临界温度公式进行了推导简化:
(2)
式中:R为气体常数,取8.314 J/(mol·K);Us为轧辊与板材变形区相对滑动速度。
Gelujiefu等[10]提出了一种接触表面间相对滑动速度的计算方法:
(3)
式中:V、Δh、h1分别为轧辊的圆周速度、压下量和轧件出口厚度。
1.2 辊缝最高温度
由布洛克滑动界面最高温度模型[11]得到辊缝最高温度的计算公式:
(4)
式中:Tmax为辊缝最高温度;A为形状系数,取决于热通量q在热源宽度w上的分布形式,热通量均匀分布时q=qav,A取1.13,半椭圆分布时A取1.11;qav为热通量分布平均值;w为热源宽度,可以近似为变形区接触弧长L;v为热源速度,可以近似为轧辊与板材变形区相对滑动速度Us。图1为假设的不规则带状移动热源模型。
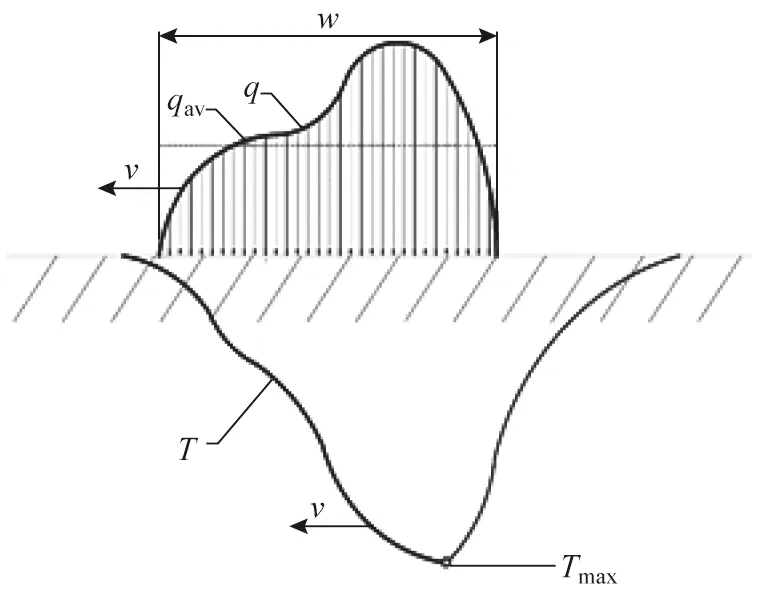
图1 移动带状热源Fig.1 Moving band-shaped heat source
根据文献[12],热通量平均分布值qav为:
(5)
式中:J为热功当量,取4.184 0 J;m为与摩擦因数μ有关的系数,根据经验取m=7;P为单位宽度轧制力,根据Hill对Bland-Ford公式简化后的公式[13]计算:
(6)
(7)
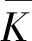
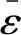
(8)
式中:ε0为本道次轧前的预变形量,ε0=(H0-h0)/H0;ε1为本道次轧后的总变形量,ε1=(H0-h1)/H0;H0、h0、h1分别为冷轧前轧件的厚度、本道次轧前轧件的厚度和本道次轧后轧件的厚度。
由于不锈钢连续冷轧时常采用张力轧制,优化后的冷轧粘着指数模型需考虑张力的影响。文献[15-16]分别给出了张力影响系数nt的计算公式:
(9)
(10)
式中:μt为加权系数,取0.7;tf、tb分别为前后张力;当无张力轧制时,张力影响系数nt=1。
由于冷轧过程中材料的变形抗力很大,轧辊会产生明显的弹性压扁现象,此时变形区长度可用西齐柯克公式计算[17]:
(11)
(12)
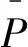
计算钢板冷轧时的摩擦因数[18]:
(13)
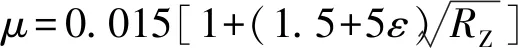
1.3 优化后的粘着指数
确定润滑油膜破裂失效的临界温度和辊缝最高温度的计算公式后,建立优化的粘着指数模型:
ξ50,σφ,γ,h0,h1,r,k,p,c,tf,tb)
(14)
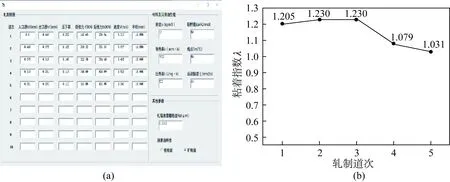
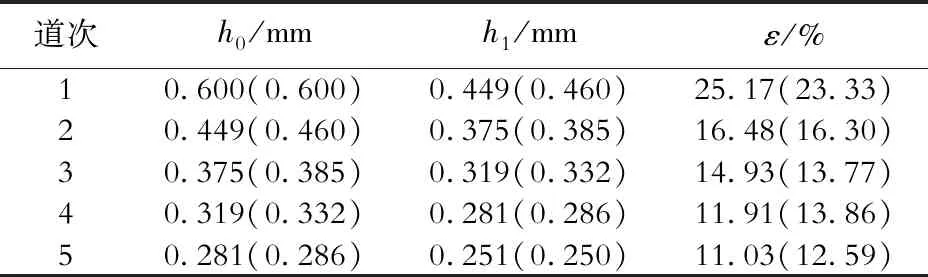
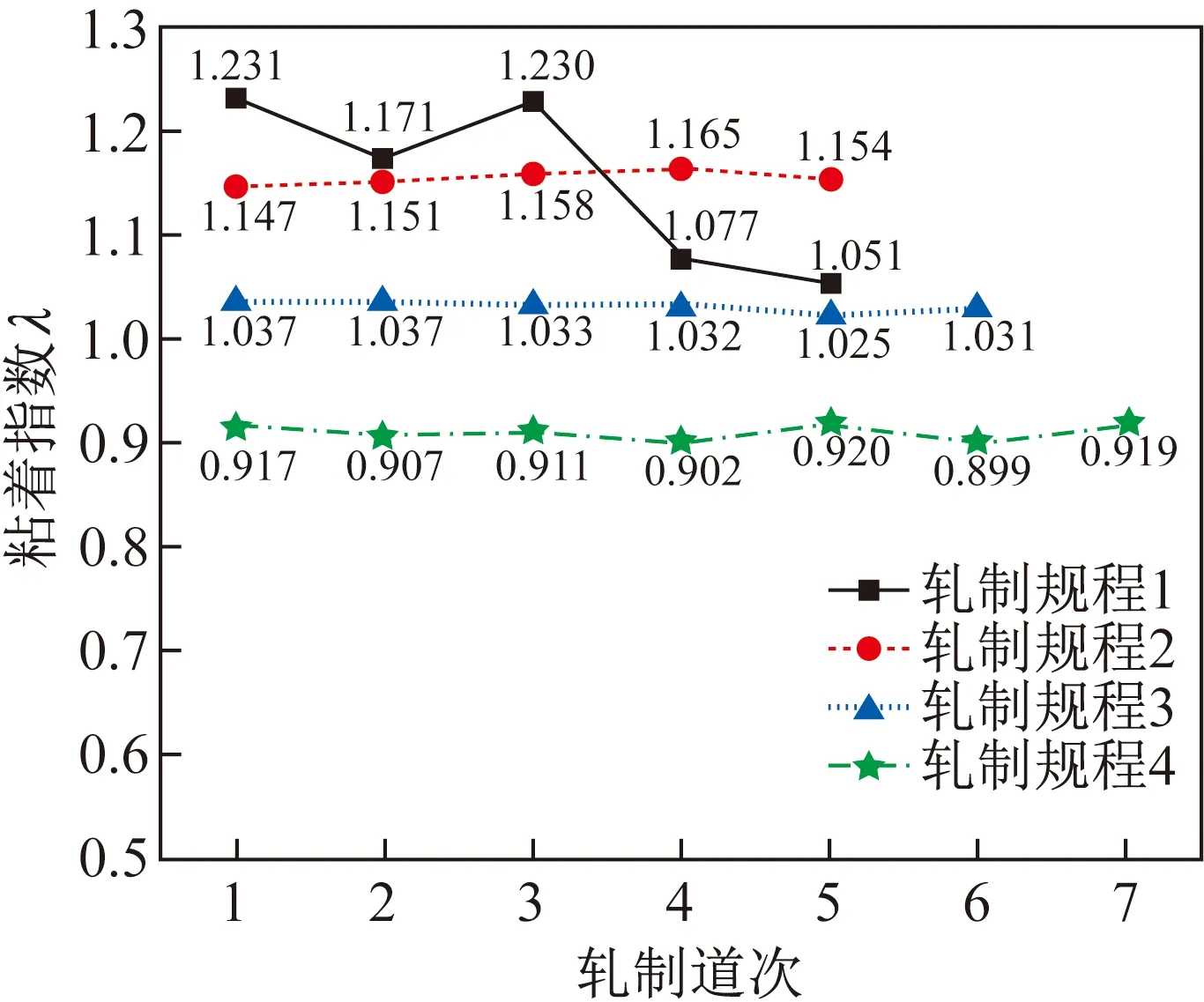
当λ′>1时,即Tmax>Tr,此时辊缝最高温度高于润滑油膜破裂失效的临界温度,润滑油发生破裂失效,容易产生粘辊现象;当λ′<1时,即Tmax 对粘着指数模型主要做了如下优化:考虑冷轧时轧辊的弹性压扁现象,使变形区长度和轧辊半径的计算更符合实际;不锈钢冷轧多采用连轧,需考虑张力的影响,将前后张力作为新的自变量添加到新模型中;结合冷轧摩擦因数的影响因子,给出了不同轧辊表面不平度时摩擦因数的计算公式,使不同状况下的摩擦因数更精确。 根据优化后的粘着指数模型,通过Visual Basic软件进行编程,具有通过输入相关自变量参数就能计算得到相应冷轧粘着指数的功能。计算机仿真软件的参数输入界面及计算结果如图3所示。 图3 计算机仿真软件的参数输入界面(a)及计算结果(b)Fig.3 Interface of parameter input(a) and calculation results(b) of computer simulation software 由式(14)可知,粘着指数λ与润滑油种类和性能、轧辊速度、压下量、材料性质、前后张力、轧辊尺寸、轧面粗糙度等因素有关。下文主要就其中的轧制规程、轧辊速度、轧辊尺寸、前后张力等因素进行探讨。 为更好地研究轧制规程对SUS304不锈钢冷轧粘着的影响,对国内某冷轧厂存在明显粘着现象的生产线进行分析。将该生产线的轧制规程命名为轧制规程1。在保持总压下量不变的前提下,改变各道次压下率,得到轧制规程2,具体数据如表1所示,表中括号外数据为轧制规程1,括号内数据为轧制规程2。为考虑单一变量,需控制其他变量保持不变,故不考虑前后张力,取轧制速度V=3.5 m/s,润滑油熔点Tm=50 ℃,运动黏度ξ50=11 mm2/s,吸附能E=50 kJ/mol,相对分子质量M=350,轧辊半径r=16 mm,原始粗糙度RZ=2.22 μm,计算两种压下规程下各机架对应的粘着指数λ值,结果如图4所示。 表1 轧制规程1和2Table 1 Rolling schedules 1 and 2 图4 轧制规程与粘着指数的关系Fig.4 Relation between rolling schedule and sticking index 从图4可以看出:由于轧制规程1各道次的压下率较大,其粘着指数整体偏大;优化后的轧制规程2各道次的粘着指数λ整体在1.1~1.2之间,但仍大于1,说明调整轧制规程能减少个别道次粘着指数较大的情况的发生,但对粘辊较严重、各道次粘着指数普遍偏高的情况,并不能有效地降低其整体粘着指数。 因此,本文提出了另一种方法来降低整体粘着指数,即增加轧制规程的道次,使每一道次的压下率降低。将轧制规程从5道次分别增加至6和7道次,具体数据如表2所示,括号内的为轧制规程3,括号外的为轧制规程4。 表2 轧制规程3和4Table 2 Rolling schedules 3 and 4 在保持其他参数不变的情况下,计算两种压下规程下各机架对应的λ值,结果如图4所示。从图4可以看出,增加了1个道次的轧制规程3各道次的粘着指数基本为1左右,增加了2个道次的轧制规程4各道次的粘着指数均小于1,说明通过增加轧制规程道次进而降低各道次压下率的方法能有效降低粘着指数。 不考虑润滑油性能的影响,在保持其他参数不变的情况下,按照轧制规程1模拟3种不同轧制速度与冷轧机各机架粘着指数的关系,如图5所示。从图5可以看出,在相同道次下,轧制速度越大,粘着指数越大,粘辊越严重。这是由于轧制速度的提高促进了变形区温度的升高,温度越高润滑膜越容易破裂,进而导致粘辊。当轧制速度超过1.5 m/s时,部分道次的粘着指数大于1,存在粘辊风险。 图5 轧制速度与粘着指数的关系Fig.5 Relation between rolling speed and sticking index 取1.5、2.5、3.5 m/s 轧制速度下轧制规程1的第1道次为研究对象,分别计算10%、15%、20%、25%压下率下的粘着指数λ。轧制规程和计算结果分别如表3和图6所示。可以看出,在轧制速度一定的情况下,随着压下率的增加,单道次粘着指数呈上升趋势。轧制速度相同时,压下率越大,粘着指数越大;压下率相同时,轧制速度越大,粘着指数越大。说明通过降低轧制速度、减小道次压下率能够有效降低粘辊程度。 表3 第1道次轧制规程Table 3 Rolling schedule of the first pass 图6 压下率与粘着指数的关系Fig.6 Relation between reduction rate and sticking index 不锈钢冷轧薄板通常用多辊轧机轧制,多辊轧机的最大特点之一就是采用小直径的工作辊。辊机的辊数越多,工作辊直径则越小,轧制带材越薄,轧制带材的最小可轧厚度与轧辊直径成正比[20]。为探究轧辊尺寸对粘着程度的影响,选取辊径分别为8、16、24 mm的3种工作辊,其他参数保持不变,计算对应的粘着指数如图7所示。从图7可知,轧辊半径越大,相同道次的粘着指数越大,说明使用更小直径的轧辊可以在一定程度上降低粘辊倾向。 图7 工作辊半径与粘着指数的关系Fig.7 Relation between roll radius and sticking index 在轧制薄带钢尤其是极薄带钢时,由于弹性变形,一定直径的轧辊不可能再对相应厚度的带钢产生压缩作用,此时只有采用张力轧制才能使薄带钢或极薄带钢变形[21],所以探究张力对轧辊粘着程度的影响十分必要。为了探究单一参数对粘着指数的影响,在原有轧制规程1的基础上,考虑前后张力的影响得到轧制规程5。 为探究张力大小对粘着指数的影响,减小前后张力得到轧制规程6,增加前后张力得到轧制规程7,分别计算3种轧制规程各机架对应的粘着指数,结果如图8所示。由图8可知:减小前后张力后,粘着指数整体略微上升;增加前后张力后,粘着指数整体略微下降,但几乎可以忽略不计。前后张力的改变会引起变形抗力和轧制压力的变化,从而影响辊缝最高温度。但从计算结果看,通过增大前后张力来降低粘着指数的方法效果并不理想。 图8 张力与粘着指数的关系Fig.8 Relation between tension and sticking index 通过调整润滑工艺可以降低冷连轧过程中轧辊的消耗,同时提高板形质量[22]。由式(13)可知,轧辊表面粗糙度和润滑油运动黏度的改变会影响摩擦因数,进而引起粘着指数的变化。在轧制规程1的基础上,选取表面粗糙度RZ分别为1.821 2、2.221 2和2.621 2 mm的轧辊计算粘着指数,结果如图9(a)所示;选取运动黏度ξ50分别为7、11和15 mm2/s的润滑油计算粘着指数,结果如图9(b)所示。可见通过降低轧辊表面粗糙度、提高润滑油黏度能够在一定程度上降低粘着指数,避免粘辊。 将优化后的粘着指数模型应用于国内某冷轧厂,对发生明显粘辊现象的生产线进行分析,将实际生产设定的工艺参数输入VB程序,计算得到的粘着指数均大于1。然后通过调整轧制规程和轧制速度等工艺参数,将粘着指数控制在1以内,再将调整后的工艺参数应用于生产线,粘辊现象得到了明显改善,证明了该模型的可靠性。 通过合理调整轧制规程,优化各道次压下率,粘着指数明显降低;在轧辊正常运行速度范围内,适当降低轧辊轧制速度能够有效降低粘着指数;在不影响正常生产的前提下,选用更小直径的轧辊能降低粘着指数;张力大小对粘着指数的影响较小;采用表面粗糙度较小的轧辊能够降低粘着指数;选用黏度较高的润滑油能够在一定程度上降低粘着指数。通过降低粘着指数,能够有效改善冷轧SUS304不锈钢产品质量,降低对轧辊的损耗,从而降低生产成本,提高生产效率。1.4 计算机模拟软件开发
2 影响粘辊程度的因素
2.1 轧制规程对粘着程度的影响
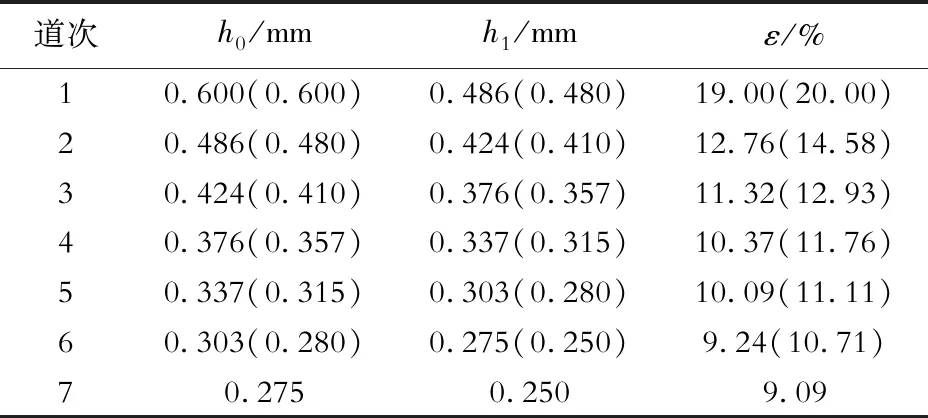
2.2 轧制速度和压下率对粘着程度的影响
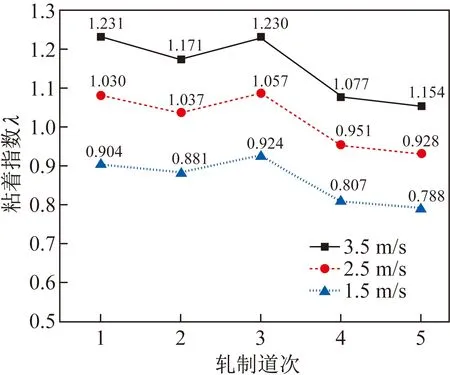
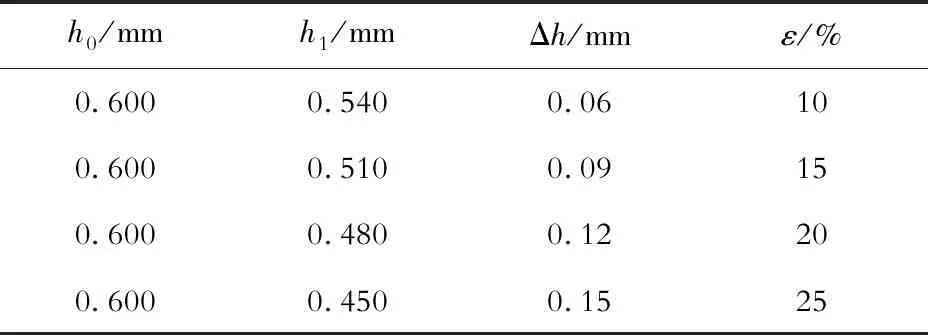
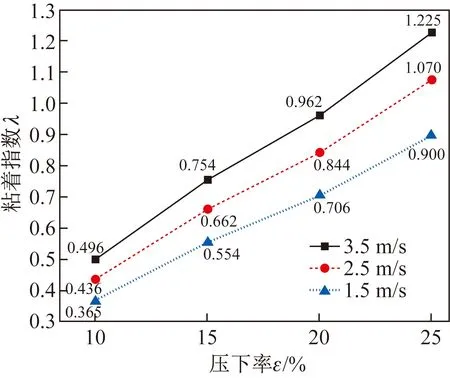
2.3 轧辊尺寸对粘着程度的影响
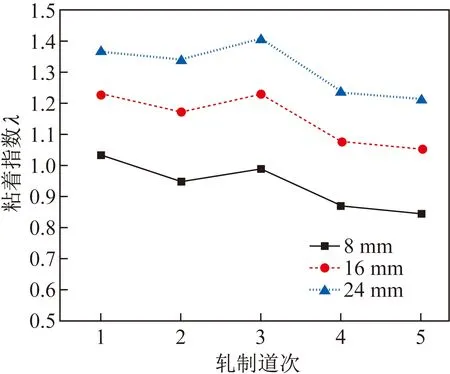
2.4 张力对粘着程度的影响
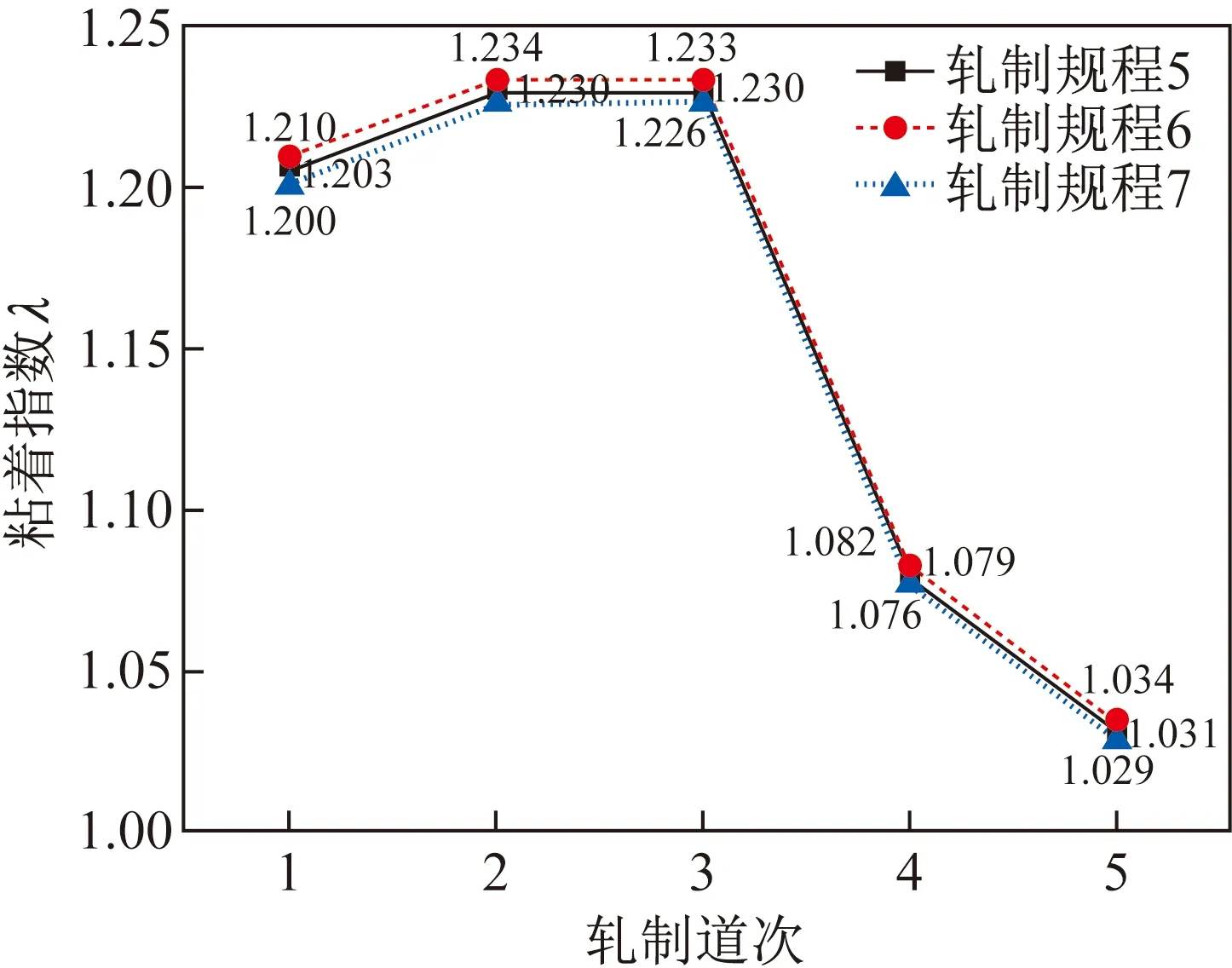
2.5 轧辊表面粗糙度和润滑油运动黏度对粘着程度的影响
2.6 现场使用效果
3 结论

