基于改进人工势场的物流无人机三维航迹规划

陈明强，冯树娟，李奇峰

(中国民用航空飞行学院 飞行技术学院，四川 广汉 618307)

0 引言

无人机作为新技术和先进生产力的重要载体,已经成为航空新业态发展的核心驱动力[1]。随着电商的兴起,最为突出的问题就是最后一公里难以送达或配送效率不高,因此物流无人机的应用随之涌现[2-4]。利用无人机技术不仅可以提高配送效率,而且可以最大限度地减少能源消耗,达到节约能源的效果。采用无人机进行配送,这一途径受到了各大物流企业的青睐,然而仍然存在一些技术上的瓶颈,阻碍了物流无人机的进一步发展。本文主要对其中的一项难题进行了研究,即物流无人机的航迹规划问题。简而言之,为了将运输物品及时、准确、安全地运送到消费者手中,规划出一条把货物从服务商的最后一站配送点送至消费者,尽可能最优、尽量避开障碍物的实际可飞的航线[5]。

孟想[6]在传统人工势场法的斥力函数中引入旋转斥力、校正因子和安全距离,并将改进后的算法应用于动态航路规划中,有效地解决了物流无人机三维航路规划问题。徐宏飞[7]在传统人工势场法中改进引力算法为固定值、引入调节分量,验证了面向智慧避障的物流无人机航迹规划模型、三维人工势场算法的有效性,但规划的路径不够平滑。张凌云[8]结合量子局部搜索和反向学习策略对狮群算法进行改进,使所求的物流无人机航迹合理可靠。但只考虑了物流无人机在实际可飞行环境中基础的物理量,忽略了一个关键的约束条件——货物质量约束。李志锟等[9]将人工势场法与蚁群算法进行融合,引入目标点距离影响因子改进斥力场函数,避免移动机器人受到较大斥力而无法实现路径规划,构造势场合力衰减系数避免了融合人工势场蚁群算法陷入局部最优解,但该方法相对复杂且仅适用于二维环境中。王兵等[10]通过引力补偿增益系数来避免引力过大的问题;对于局部极小值点问题根据环境信息采取不同的虚拟目标点来解决,提高了安全性,缩短了路径长度。但只在二维环境中进行了仿真验证,并没有扩展至三维环境中。Fan等[11]提出的改进人工势场算法主要思想是构建一个虚拟正六边形模型,当运动目标陷入局部极小值时,利用正六边形模型引导运动目标跳出局部极小值的陷阱。虽然该方法解决了传统人工势场法局部极小值的问题,但存在路径震荡和转弯角过大的问题。

本文针对传统人工势场算法目标不可达和局部极小值的缺点,设计了一种改进的人工势场算法。通过在斥力势场函数中添加无人机和目标点之间的相对距离来解决目标不可达问题。采用球体模型策略有效地改善局部极小值问题。

1 无人机的性能约束

物流无人机的货物运输需要从多方面进行考虑,本文从物流无人机性能约束和任务要求两方面着手,建立多约束条件下的物流无人机航迹规划模型。设物流无人机运输任务的区域是以长、宽、高分别为x、y、z的空间环境。

1.1 最远航程约束

判断航迹规划好与不好的一个重要因素是规划的航迹长度,在满足各种需求的条件下规划的航迹越短越好。因此物流无人机的运输距离不得大于最远航程,(xi,yi,zi)表示无人机在三维空间直角坐标系中第i个点的位置,约束为:

(1)

di≤dmax,

(2)

式中:dmax为无人机最远航程。

1.2 最大货物质量约束

物流无人机能够承载货物的质量是有限的,物流无人机的总质量由物流无人机自身质量及货物质量两部分组成。而物流无人机自身的质量是恒定不变的,所以只能对货物进行限制。上限约束为:

M=m+n,

(3)

n≤nmax,

(4)

式中:m为物流无人机自身的质量,n为货物的质量,nmax为最大载货质量。

1.3 飞行高度约束

物流无人机在飞行的过程中受到自身性能和货物的影响,飞行高度应该限制在最低飞行高度和最高飞行高度之间。约束为:

hmin≤h≤hmax,

(5)

式中:hmin为最低飞行高度,hmax为最高飞行高度。

1.4 俯仰角约束

为了保证物流无人机运输的整体安全,物流无人机在持续飞行过程中的垂直旋转角度受到限制,不可能实现革命性的大角度旋转[7],约束为:

(6)

式中:b为最大俯仰角。

2 传统人工势场法及其缺陷

2.1 传统人工势场法

传统人工势场(Traditional Artificial Potential Field, TAPF)法是由Khatib于1985年提出的一种解决路径规划的有效方法[12],其核心思想是构造虚拟势场,目标位置会对无人机产生引力Fatt作用,障碍物在一定范围内对无人机产生斥力Frep作用,最终在二者的合力F作用下使得无人机沿着无碰撞的轨迹运动至目标位置。无人机受力图如图1所示。

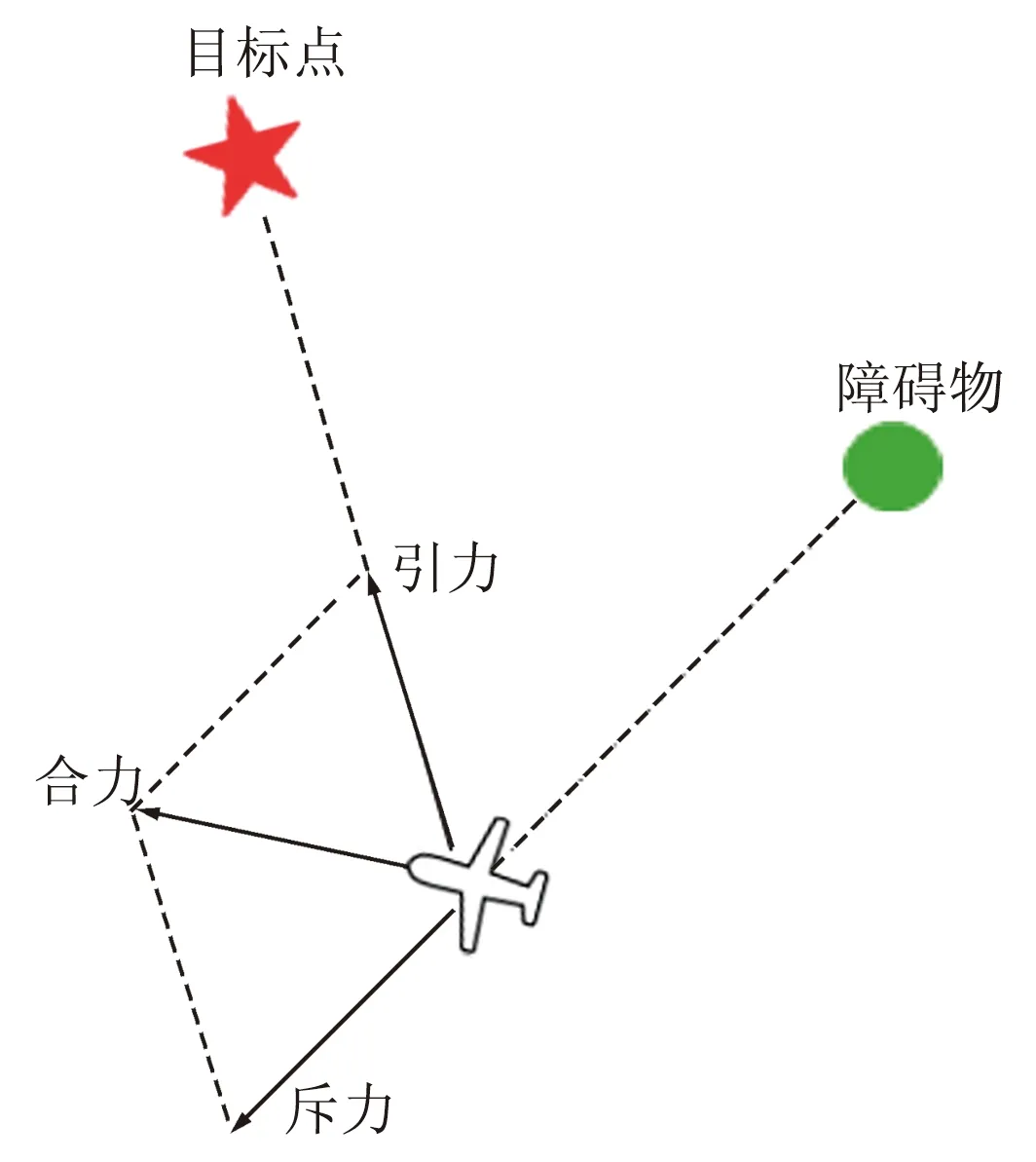
图1 无人机受力图Fig.1 Drone force diagram

引力势场函数:

Uatt(X)=0.5kattρ2(X,Xg),

(7)

引力函数:

Fatt(X)=-▽Uatt(X)=-kattρ(X,Xg),

(8)

斥力势场函数:

(9)

斥力函数:

Frep(X)=-▽Urep(X)=

(10)

合力:

F(X)=Fatt(X)+Frep(X),

(11)

式中:Xg表示目标点位置,Xo表示障碍物位置,katt表示引力增益系数,krep表示斥力增益系数,ρ表示2点之间的距离,ρ0表示斥力作用范围,Fatt为势场Uatt的负梯度,Frep为势场Urep的负梯度,F为无人机所受到的合力。

2.2 TAPF法的缺陷

2.2.1 目标不可达

物体在目标点附近时斥力大于引力,此时物流无人机无法到达目标点的情况称为目标不可达问题[13]。如图2所示。

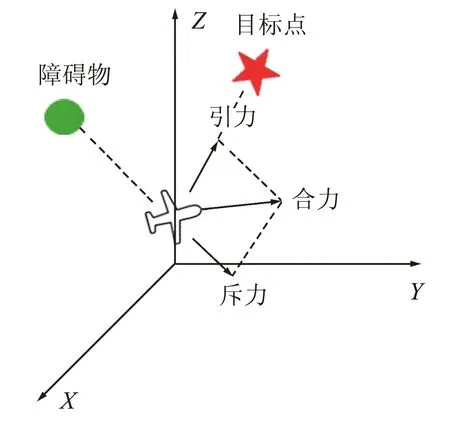
图2 目标不可达示意Fig.2 Schematic of unreachable target

2.2.2 局部最优

当物流无人机、目标点以及障碍物在同一直线上时总会出现一点使得引力和斥力大小相等、方向相反且合力为零,此时无人机就陷入局部极小值,如图3所示。为了解决该问题,本文提出基于改进人工势场法的无人机三维航迹规划。

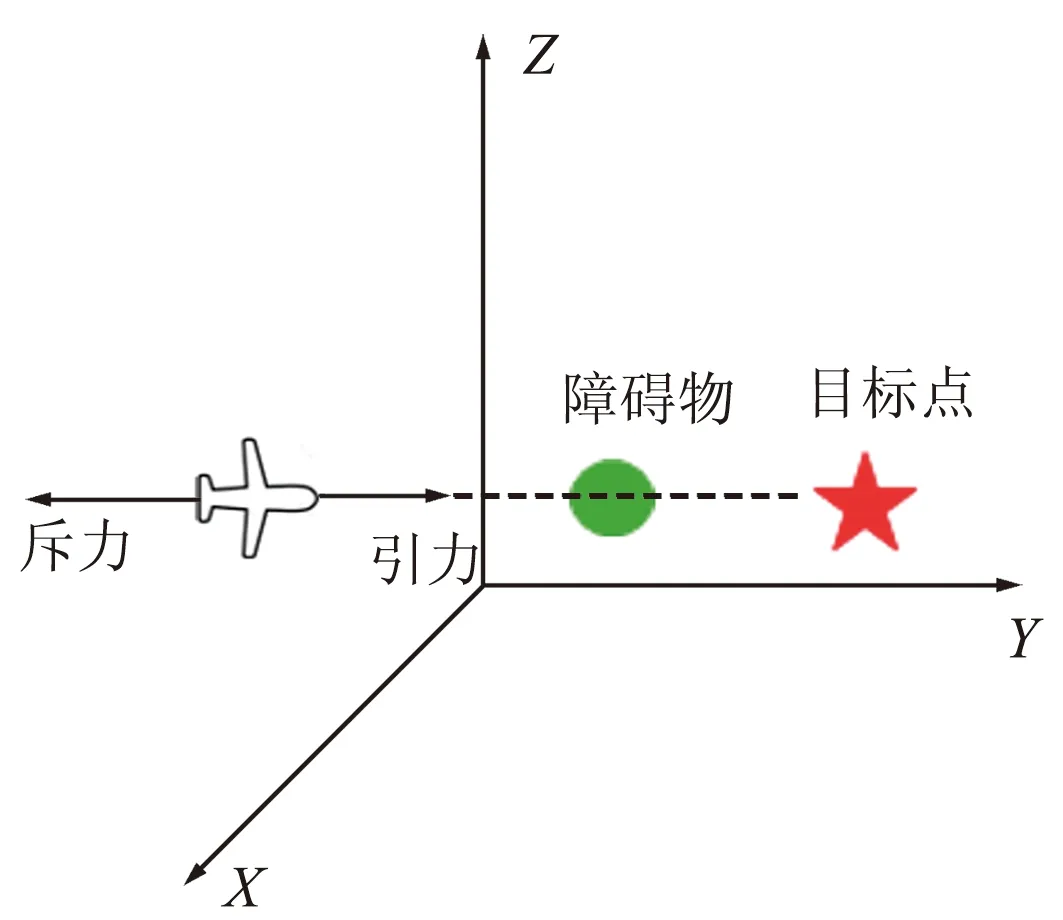
图3 局部极小值示意Fig.3 Schematic of local minimums

3 TAPF算法的改进

3.1 改进斥力函数

针对目标不可达的问题,常用的方法是在斥力势场函数中添加无人机和目标点之间的相对距离[14]。

改进后的斥力势场函数:

(12)

改进后的斥力函数:

Frep(X)=-▽Urep(X)=

(13)

(14)

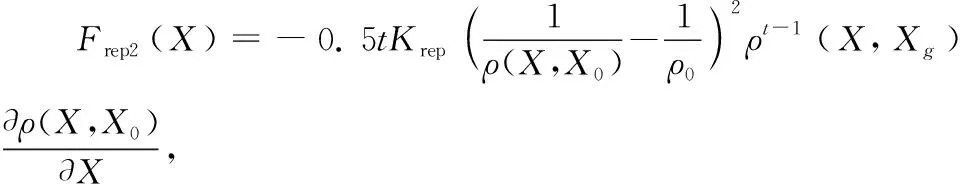
(15)

ρt(X,Xg)=|(x-xg)t|+|(y-yg)t|+|(z-zg)t|。

(16)

式(13)中的Frep1和Frep2见式(14)和式(15)。式(16)为无人机和目标点之间的相对距离,t可取大于零的任意常数。Frep1的方向是障碍物与无人机之间的连线并指向无人机,Frep2的方向是无人机与目标点之间的连线并指向目标点。无人机受力分析如图4所示。

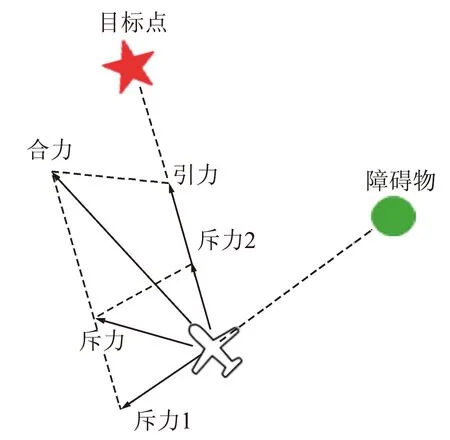
图4 改进斥力后无人机受力图Fig.4 Drone force diagram with improved repulsion

随着t的取值发生变化,物流无人机的受力情况也随之发生变化。接下来对t进行分类讨论:

① 当t为0～1时,

(17)

(18)

因此,当t为0～1时,随着物流无人机和目标点之间的距离不断减小,Frep1(X)趋向于0,Frep2(X)趋向于∞,而Frep2(X)的方向是物流无人机与目标点之间的连线并指向目标点。此时无人机只受到斥力分量Frep2(X)和引力Fatt的作用,所以物流无人机在共同力的作用下朝着目标点的方向运动。

② 当t=1时,

(19)

(20)

因此,当t=1时,随着物流无人机和目标点之间的距离不断减小,Frep1(X)趋向于0,Frep2(X)趋向于-0.5Krep(1/ρ(X,X0)-1/ρ0)2,而Frep2(X)的方向是物流无人机与目标点之间的连线并指向目标点。此时无人机只受到斥力分量Frep2(X)和引力Fatt的作用,所以物流无人机在共同力的作用下朝着目标点的方向运动。

③ 当t﹥1时,

(21)

(22)

因此,当t﹥1时,随着物流无人机和目标点之间的距离不断缩小,Frep1(X)趋向于0,Frep2(X)趋向于0,此时无人机只受到引力Fatt的作用不受斥力的影响,且在引力的作用下使物流无人机朝着目标点的方向运动。

由此可知,无论t取任何大于零的常数时,斥力分量Frep1(X)都趋向于0,所以物流无人机在运动的过程中只受到斥力分量Frep2(X)和目标引力Fatt的影响。而斥力分量Frep2(X)以及引力Fatt的方向均是物流无人机与目标点之间的连线并指向目标点的,因此,当目标点与障碍物之间的距离较近时,物流无人机也能够在斥力分量Frep2(X)和引力Fatt二者合力的共同作用下安全到达目标点。

3.2 球体模型策略

考虑到物流无人机在复杂环境下可能遇到多个局部极小值点问题,无法直接到达目标点,提出一种球体模型策略,通过在合适的位置设定虚拟目标点,打破原有力的平衡,使物流无人机在障碍物、目标点以及虚拟目标点的共同作用下跳出局部极小值陷阱,继续向目标点移动。

首先,需要判断物流无人机是否陷入局部极小值点。当物流无人机陷入局部极小值时,就会在某一点暂停或是在特别小的范围内前后移动,本文通过设定一个阈值与第i(i≥2) 次迭代时的位置和第i+1次迭代时的位置之间的相对距离进行比较,若2个点位置之间的相对距离小于设定的阈值,则物流无人机陷入局部极小值的陷阱;反之,则没有[15-17]。或依据合力是否为0判断物流无人机是否陷入局部极小值的陷阱。

针对上述问题,本文提出一种球体模型策略来解决。具体如下:若物流无人机陷入局部极小值,则以物流无人机陷入局部极小值为原点,建立三维空间直角坐标系XYZ,如图5所示。本文把障碍物及其影响范围抽象为一个球体(图中的橙色区域),该球体是以障碍物的坐标(O)为球心,障碍物的影响范围(r)为半径。在XYZ坐标系中画一个以局部极小值点为球心,局部极小值点(A)和目标点(G)的欧式距离为半径(s)的球体N。物流无人机在局部极小值点扫射障碍物,以障碍物影响范围的边界为切点会有无数条切线,这些切线会与球体N相交形成一个圆(圆心为e,半径为R,图中的紫色区域),圆上的点可作为虚拟目标点,从而使物流无人机跳出局部最小值的陷阱。

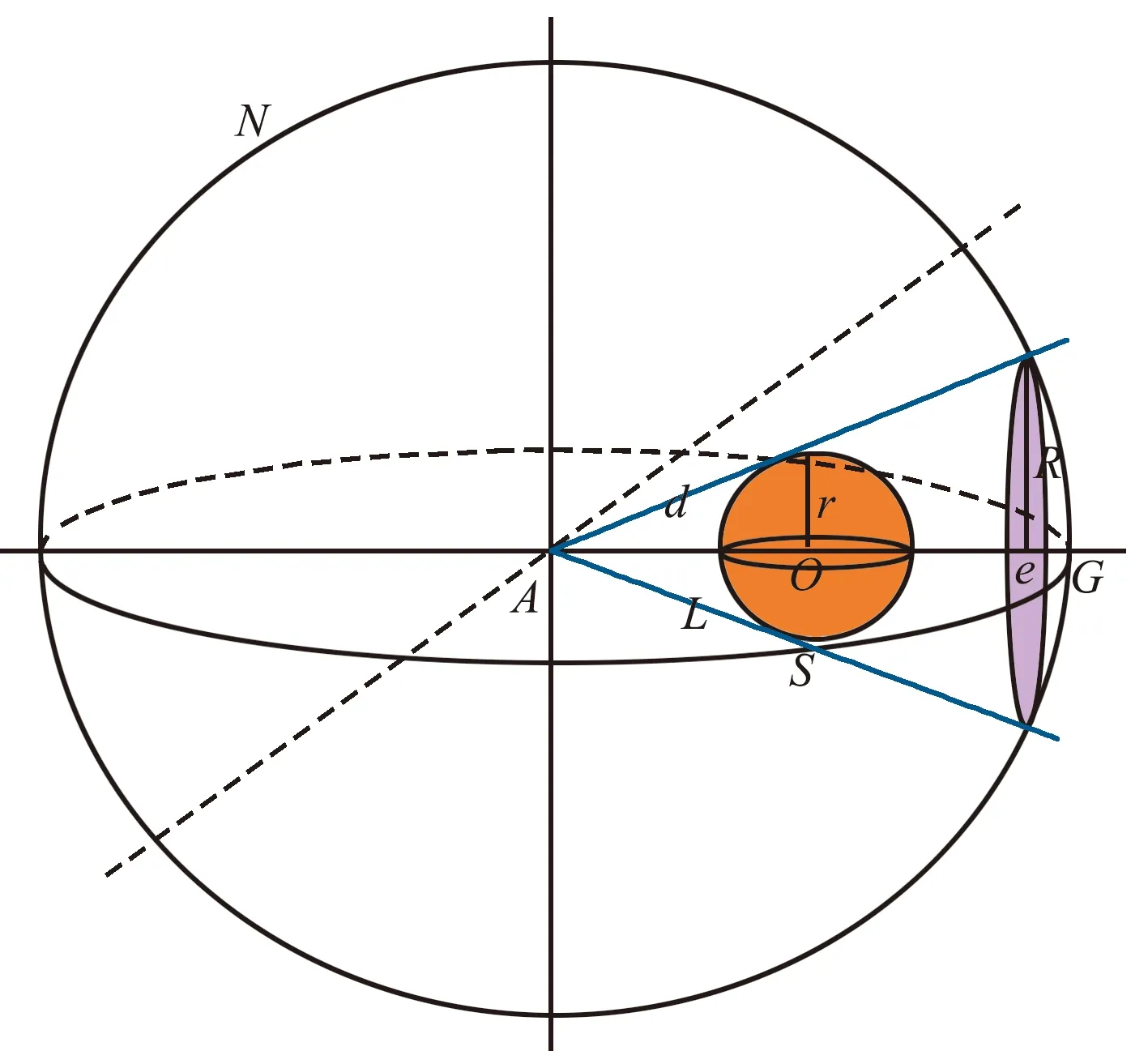
图5 球体模型Fig.5 Sphere model

设空间中的局部极小值点坐标为A(x1,y1,z1),障碍物的坐标为O(x0,y0,z0),目标点为G(xg,yg,zg),建立模型。

局部极小值与障碍物之间的距离:

(23)

局部极小值与切点之间的距离:

(24)

局部极小值与目标点之间的距离:

(25)

由式(24)和式(25)得圆的半径:

(26)

带入参数得:

(27)

由式(23)、式(24)和式(25)得圆心:

(28)

带入参数得:

(29)

由式(27)和式(29)得圆的标准方程:

[x-(x1+e)]2+(y-yg)2=R2。

(30)

带入参数得:

(31)

局部极小值问题通过在空间坐标系XYZ中设立虚拟目标点进行处理。当物流无人机陷入局部极小值的陷阱后,通过采用球体模型策略的方法在目标点附近建立虚拟目标点进行处理,使无人机跳出局部极小值的陷阱,顺利到达目标点。设立虚拟目标点后物流无人机受力分析如图6所示。

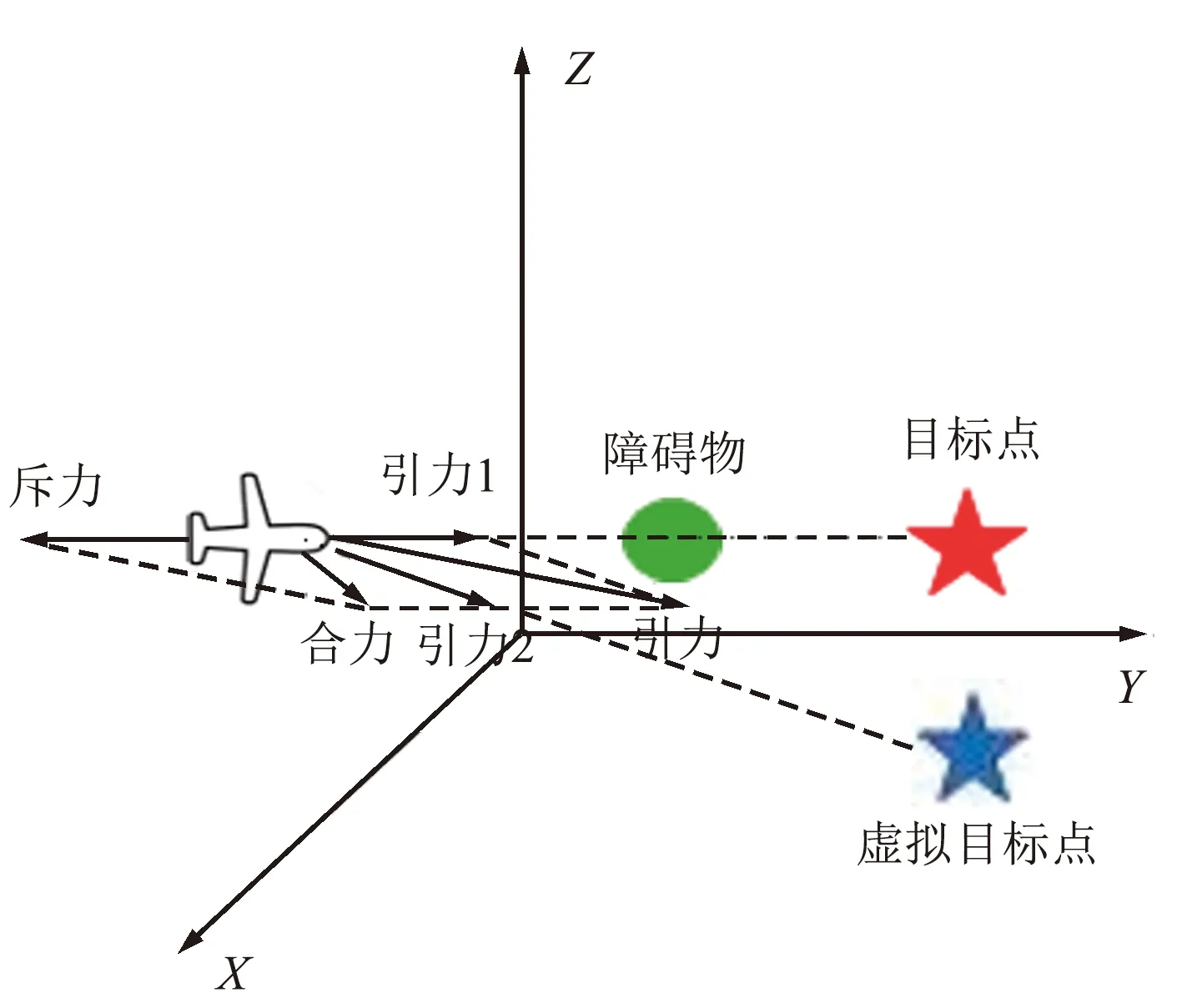
图6 设立虚拟目标点后无人机受力图Fig.6 Drone force diagram after setting up a virtual target point

3.3 算法流程

改进后的算法流程如下:

① 初始化参数,设置物流无人机的初始位置、目标点位置和障碍物的位置。

② 根据式(8)、式(11)和式(13)计算合力。

③ 依据合力是否为零判断物流无人机是否陷入局部极小值的陷阱,若是则转至步骤④;否则转至步骤⑤。

④ 采用球体模型的策略使物流无人机跳出局部极小值的陷阱。

⑤ 以改进后的人工势场法驱动物流无人机继续向前行驶,判断物流无人机是否到达目标点,若是则转至步骤⑥;否则转至步骤② 继续进行迭代。

⑥ 结束流程。

算法流程如图7所示。

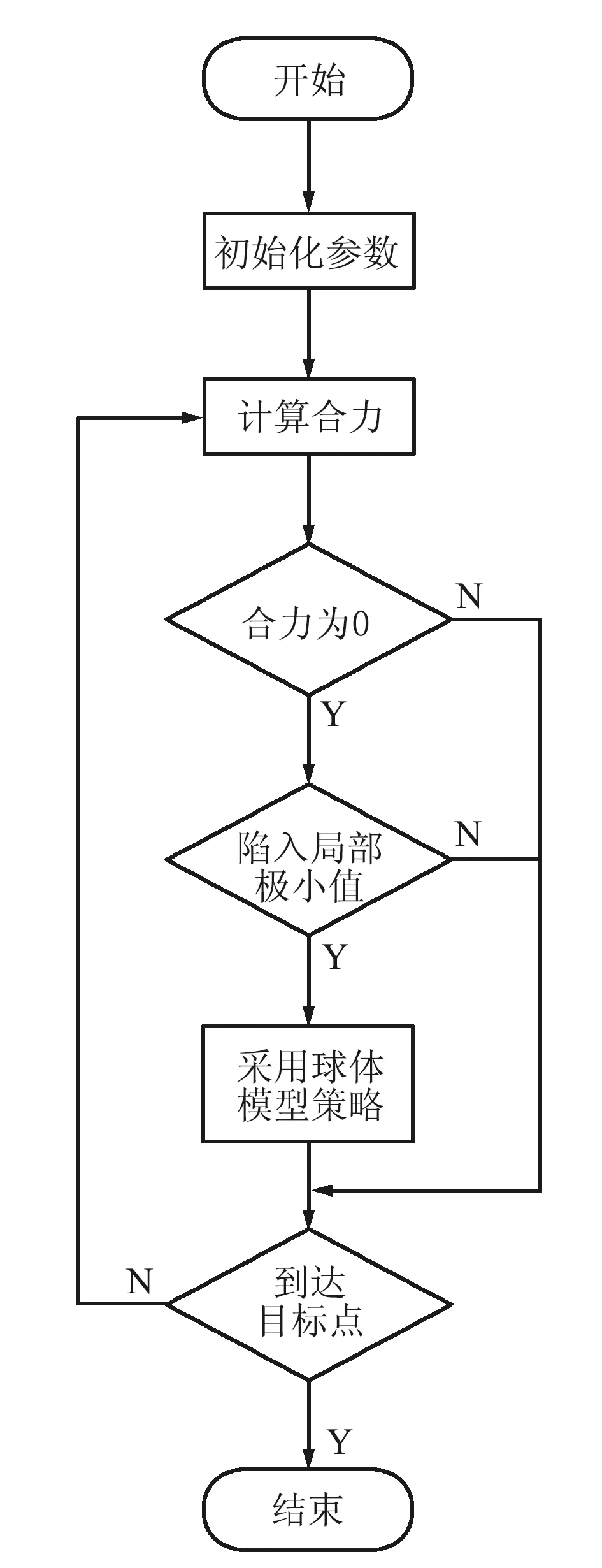
图7 算法流程Fig.7 Algorithm flowchart

4 仿真分析

4.1 基于改进斥力函数的仿真

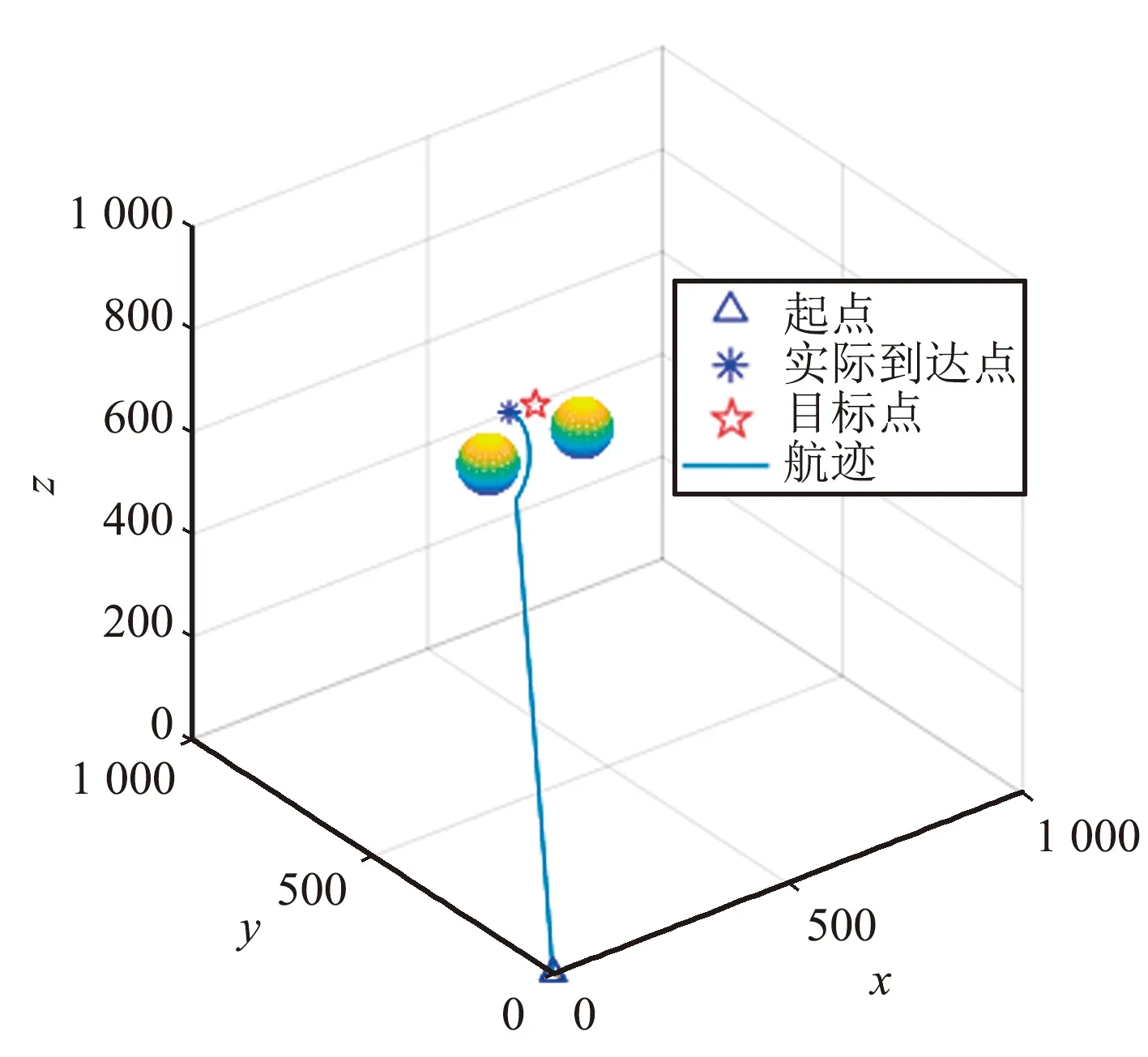
图8 目标不可达仿真结果Fig.8 Simulation results for unreachable target

在斥力势场函数中添加无人机和目标点之间的相对距离,解决了上述目标不可达的问题,仿真结果如图9所示。可以看出,实际到达点和目标点重合,即物流无人机到达目标点。

图9 改进斥力函数仿真结果Fig.9 Simulation results for improved repulsion function

4.2 球体模型策略的仿真

为了验证本文所提出的球体模型策略对物流无人机跳出局部极小值陷阱的有效性,在Matlab仿真软件上进行仿真实验。设物流无人机的起始点为(0,0,0),终点为(900,900,900)。在只有一个障碍物的环境中,障碍物的坐标为(313,313,313)。由于起点、障碍物和终点3点共线,且在其中的一点合力为0,导致传统人工势场法陷入局部极值的陷阱,如图10所示。

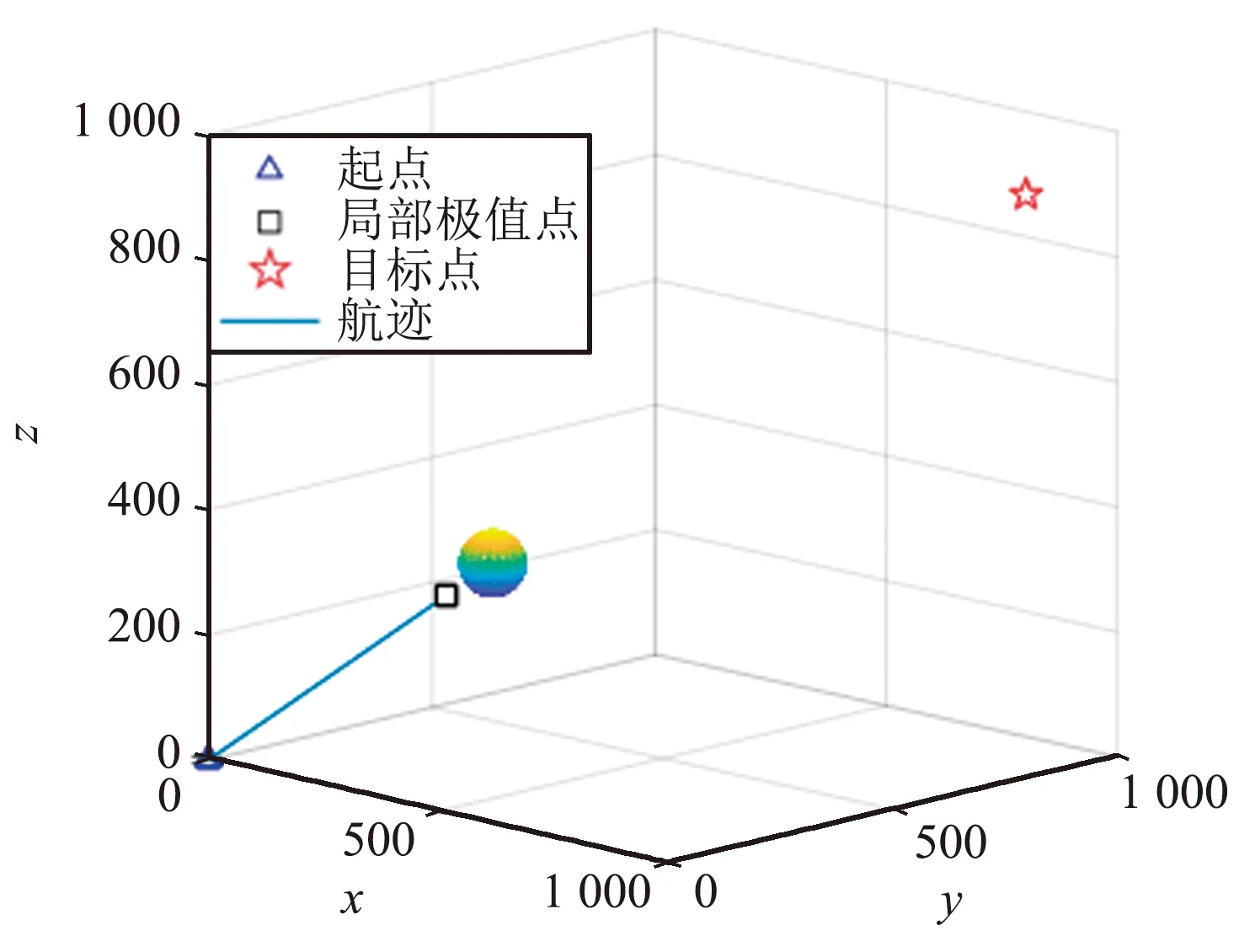
图10 局部最优仿真结果Fig.10 Simulation results for local optimal solution

判断物流无人机已陷入局部极小值的陷阱,用本文提出的球体模型策略,产生虚拟目标点,打破原有力的平衡,使物流无人机跳出局部极小值的陷阱并安全到达目标点,球体模型策略规划结果如图11所示。

图11 单障碍物球体模型策略规划结果Fig.11 Planning results for single-obstacle sphere model strategy

上述仿真实验验证的是在只有一个碍物的场景中,当物流无人机陷入局部极值的陷阱时采用球体模型的策略跳出局部极小值陷阱是可行且有效的。接下来进行多障碍物情景中物流无人机的运动。设起点坐标(0,0,0),终点坐标(900,900,900),障碍物坐标分别为(313,313,313)、(400,700,100)、(530,610,600)、(800,750,300)、(700,400,600)、(730,710,710)、(132,625,440),使用TAPF法进行仿真,结果如图12所示。

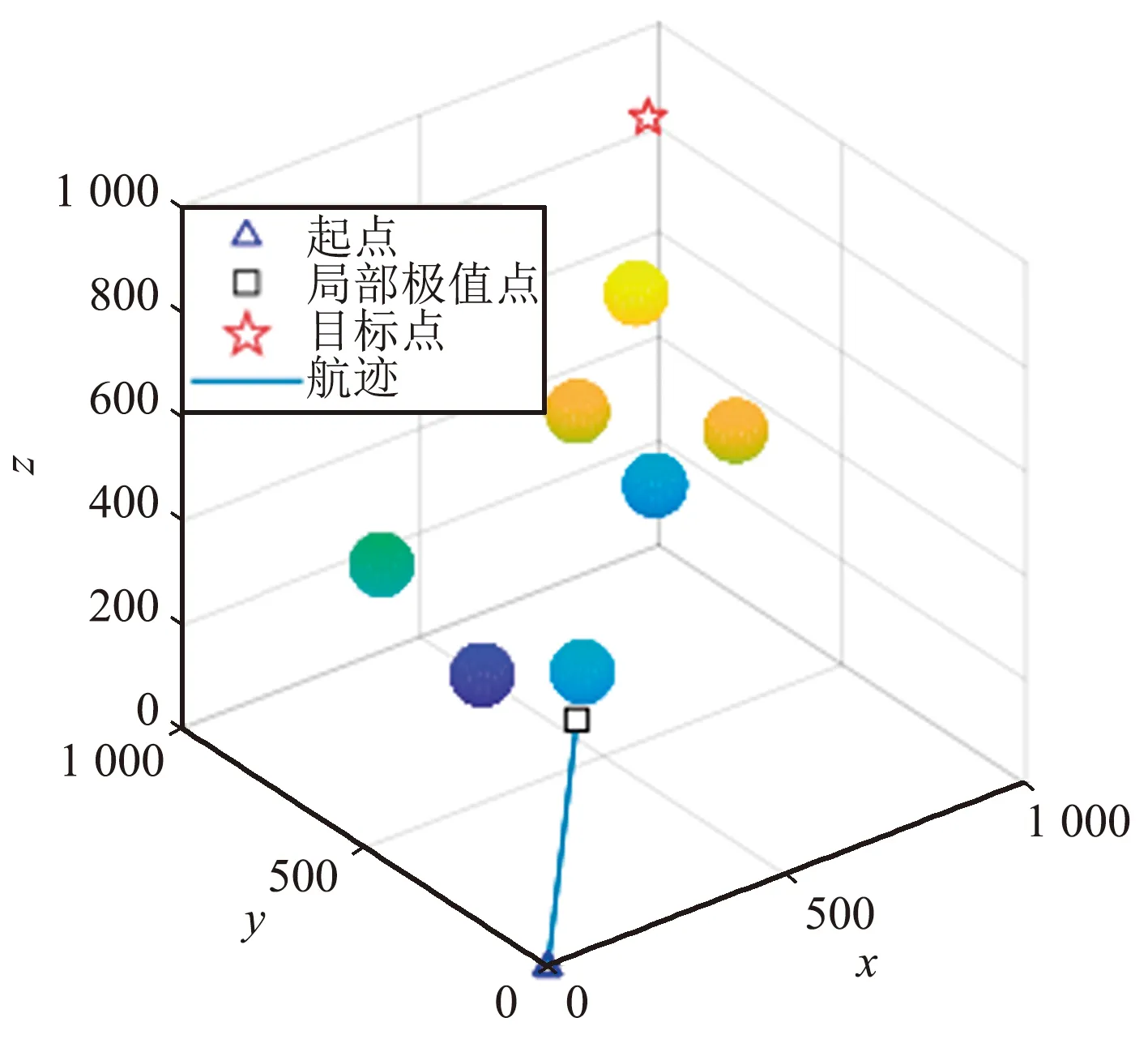
图12 TAPF法规划结果Fig.12 Planning results for TAPF method

由图12可以看出,当前物流无人机已陷入局部极小值陷阱,采用本文提出的球体模型的策略,产生虚拟目标点,打破原有力的平衡,使物流无人机跳出局部极小值的陷阱并安全到达目标点,如图13所示。

图13 多障碍物球体模型策略规划结果Fig.13 Planning results for multi-obstacle sphere model strategy

通过上述2组实验可以看出,物流无人机灵巧地避开了所有障碍物,逃离局部极小点的陷阱,到达最终目标点。验证了本文提出的改进人工势场方法尤其是球体模型策略在物流无人机三维航迹规划中的可行性。

5 结束语

本文针对物流无人机三维航迹规划问题,分析了TAPF法及其存在的缺陷并提出了解决方案。通过改变斥力势场函数解决目标不可达问题;当无人机处于局部极值时,采用球体模型策略构造虚拟目标点使无人机在障碍物的斥力、目标点的引力以及虚拟目标点引力的共同作用下解决局部极小值问题。仿真结果显示,改进的人工势场法能够有效地规划出符合要求的最佳航迹,使物流无人机成功避开所有障碍物,安全到达目标点。