一种IGrubbs-LWLR的区域高程异常拟合方法

张 炎，刘立龙，蒙金龙，徐 勇，何广焕，胡鹏程

(1. 桂林理工大学 测绘地理信息学院，广西 桂林 541006；2.广西空间信息与测绘重点实验室，广西 桂林 541006；3.广西建设职业技术学院 市政与交通学院，广西 南宁 530007)

0 引言

现今通过全球导航卫星系统(Global Navigation Satellite System,GNSS)获取地理信息数据已成为空间大地测量领域的一种重要手段,该技术所采集的高程值是以WGS-84参考椭球面为基准的大地高[1-2]。实际工程中,常常采用以似大地水准面为基准的正常高,二者之间存在的差值,即为高程异常值[3]。外野采集的数据中往往存在一定的粗差,剔除粗差及选定合适的高程异常预测模型的拟合方法是在工程项目中完成测高工作的重要内容[4]。对于观测值中的粗差判别/剔除,目前常用的方法有格拉布斯(Grubbs)法则、t检验法和稳健估计法等,针对不同的样本总量及所存异常值比例,选用不同的方法进行粗差识别及剔除的效果也不尽相同[5-7]。韩红超[8]利用Grubbs检验法对某市的沉降监测数据进行粗差探测和剔除,证明了Grubbs法应用于大量数据中的粗差探测的可行性,取得了良好的效果。在完成原始测量数据中的粗差剔除后,拟合方法的选择也极为重要,常用的多面函数法、样条曲线拟合法、支持向量机等在面对山峰突起且山体分布不规则的情况时,所建高程异常拟合模型的效果不理想,其精度也难以满足实际测绘生产的需求[9]。

本文提出一种改进格拉布斯法(Improved Grubbs,IGrubbs)结合局部加权线性回归(Local Weighted Linear Regression,LWLR)组合算法来构建区域高程异常拟合模型。在原Grubbs的基础上,引入自适应迭代,构建新的评判指标参数,来提高Grubbs法则对测量数据中粗差的判别及剔除效率。通过LWLR法对预处理后的高程异常数据进行拟合,完成精度较高的区域高程异常预测模型的建立,为以后的测高工作提供一定的参考。

1 原理与方法

1.1 Grubbs法则

在样本总体标准差未知的情况下,Grubbs通过对服从正态样本或接近服从正态样本的数据进行异常判决[10-11]。计算公式如下:

(1)

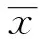
(2)

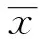
1.2 IGrubbs粗差剔除法

在对测量数据中的粗差进行判定及识别时,若样本方差偏大或偏小,将会存在对之后的样本产生误判或漏判的可能[12]。特别是在样本中非零值估计偏差受异常值影响过大时,会导致后续样本总量偏低,发生错误识别及判定的机率将会提高[13]。为了有效避免误判及漏判的情况发生,对原Grubbs作出改进,具体如下:

① 引入自适应迭代。以样本长度作为自适应迭代参数进行循环判定,从而确保样本中所有数值得到充分检验。

② 设定粗差剔除完成的指标参数。在剔除粗差的过程中,以观测值残差与标准差的比值与Grubbs临界值的差作为粗差剔除完成的指标参数。在对测量数据的粗差识别及判定的过程中,当样本中所有数据均已低于对应的Grubbs临界值时,表明当前样本中已不存在异常值,则退出自适应迭代,不再进行冗余运算。指标参数flag具体如下:

(3)

式中:数据组U为储存所有样本数据的动态数组,Gi为最大偏离值,Gg为Grubbs临界值与标准差的乘积,L为数据组U的样本总量。

当原始测量数据中存在粗差值时,IGrubbs对其进行识别及判定的具体步骤如下:

① 数据初步处理:原始样本数据为存在粗差的所有测量点,构成三维(平面坐标及高程异常)数组U,获取每个高程异常值所对应的平面坐标的位置索引,将U中高程异常值按从小到大的顺序排列,随后计算U中样本长度L0,L0的大小即为自适应迭代参数控制最大迭代次数T,从而保证样本中所有数值得到充分检验。

② 分配IGrubbs临界值区间:IGrubbs临界值区间由选定的置信区间及样本长度L决定,当置信水平α=95.00%时则选取对应95.00%置信区间的IGrubbs临界值进行异常值判定,随着置信水平值的变大,其对应的异常判定严密程度也更为强烈。通常情况下,置信区间的选取应为适中状态,过高或过低均难以达到最佳的粗差识别目的。根据前者的研究经验,实验时在对高程异常数据中的粗差识别过程中选择置信水平为95.00%或97.50%时置信区间所对应的IGrubbs临界值来作为粗差判定的标准。

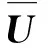
图1 IGrubb粗差剔除流程Fig.1 The process of gross error elimination based on IGrubbs method

1.3 LWLR算法

在对训练样本数据进行预处理后,利用LWLR法来构建区域高程异常拟合模型。线性回归法求的是具有小均方误差的无偏估计,回归曲线受整体影响较大,易形成欠拟合现象[14-15]。与之相比,LWLR法的优势在于每一次迭代预测时都会更新权值,重新确定拟合系数,从而使拟合面逐渐逼近真实值[16]。在着重考虑到局部点的同时,也使局部以外的整体数据参与到拟合曲线中来,更适用于非线性变化的高程异常数据的拟合及预测。具体内容如下:

若存在m个高程拟合点,(xi,yi)为拟合点平面坐标,f(xi,yi)为曲面拟合函数,vi为残差,ξi为对应的高程异常值,则已知点与高程异常值的关系可表示为:

(4)

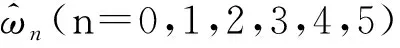
(5)

(6)

通过测量获取的高程异常数据集来构建一定范围内连续变化的坐标曲面函数,若选择的拟合点分布不均匀或未选择到能够代表地形起伏的特征点,则最终形成的拟合面将与实际相差较大。因此,在式(6)的基础上,引入距离定权的权重矩阵W,以拟合点与检核点的距离作为评判二者相关程度的标准,使拟合函数能够较为准确地反映出周围地形起伏变化的状态,从而有效降低拟合点远离检核点对拟合模型产生的负面效果[17]。加入权重后的公式如下:

(7)

式中:本文选择高斯核函数的权重作为其权重系数。

(8)

式中:di为检核点到拟合点的距离,(xi,yi)为拟合点平面坐标,(ej,fj)为检核点平面坐标,g为检核点数,k为波长。

1.4 拟合模型的构建

在工程测高工作中,粗差往往是难以避免的,若未能得到及时处理,将会对后期项目中待测点获取的高程精度产生严重影响。本文利用IGrubbs-LWLR组合法来完成粗差的剔除及待测点的高程预测工作,建立较高精度的区域高程异常拟合模型。具体过程如下:

① 对训练样本数据进行初步处理,读取数据集。

每名学生都必须参加出科考核，考核内容包括病史询问、体格检查、病历书写及技能操作。除病历书写外其他项均由总住院医师负责考核，病历书写由总住院医师协助主治医师实施考核。在考核中，总住院医师应关注每名学生的成绩，给出客观、真实的评价，指出学生存在的问题，并给予相应指导；同时对于学生做得好的方面，给予表扬和鼓励，真正做到以考促学。4重视实习生反馈意见，不断改进教学方法

② 记录数据组所对应位置索引并排序。选取置信区间,确定Grubbs临界值区间。

④ 迭代开始,对待检点进行粗差识别,调用格拉布斯临界值λ(a,n),判断该点的Gi是否大于λ(a,n)与标准差E的乘积,若Gi大于λ(a,n),将该点视为可疑值并记录,保存该可疑点;若Gi小于λ(a,n),则表明该检测点中未含有粗差值,不做记录及保存。

⑤ 对第一个待测点判别完成后,则迭代进入下一个待测点的粗差识别工作,返回至步骤④中进行。直到迭代次数达到最大值时,训练样本数据中的粗差判定完毕,统计训练样本中含有粗差的数值,并对其进行剔除,整理获取新的训练样本集。

⑥ 对剔除粗差后的训练数据集作出归一化处理,利用LWLR法来构建区域高程异常拟合模型。

⑦ 输入预处理后的训练数据与测试数据,设置参数k初始值及最大迭代次数Tm。

⑩ 判断当前的均方误差值是否满足阈值或者达到最大迭代次数,若满足条件,迭代停止,记录并保存当前模型的相关系数及预测值,此时所构建的区域高程异常拟合模型的精度最佳;若未满足条件,更新参数k(k=k+0.05),重复步骤⑧、⑨,直至达到限定条件位置,输出结果,迭代停止。

2 实例分析

实验数据选定为广西东北小范围山地区域内的采集的74个GNSS水准重合点(四等水准测量要求,部分点含有粗差),用于后期区域高程异常拟合模型建立及精度检验。研究区域内点位分布较为均匀,2个GNSS水准重合点间隔在2.5 km范围内,总区域覆盖面积约为300 km2。均匀选取其中的59个GNSS水准重合点作为模型的训练样本集,剩余的15个重合点作为拟合模型精度的检核点。

2.1 IGrubbs剔除粗差

为确保拟合模型的精确度及可靠性,通过IGrubbs对参与模型构建的高程异常值进行预处理,剔除存在粗差的数据。同时选用传统Grubbs作对比分析,设置不同的置信区间,对59个建模点进行粗差探测/剔除,2种算法在α=99.5%的高置信水平下包含了低置信区间剔除的所有可疑点。最终,传统Grubbs筛选出高程异常值分别为20.553、19.258、20.856 m的3个可疑点,IGrubbs筛选出高程异常值分别为20.553、19.258、19.363、20.856、20.461 m的5个可疑点。具体的效果对比如表1所示。

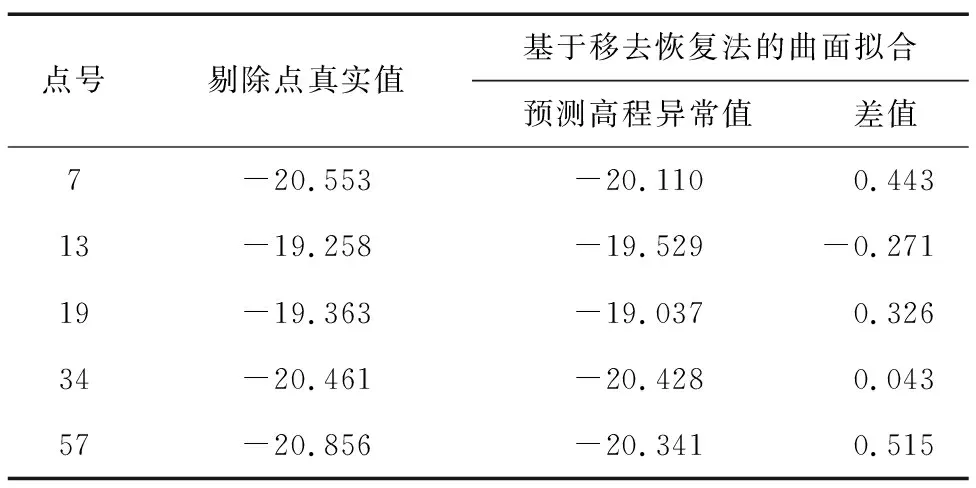
表1 剔除点的检核统计表Tab.1 The check statistics of elimination points 单位:m

为了检验2种方法是否存在粗差误判的情况,选用常规移去恢复法的二次曲面对疑似点周边的数个GNSS水准重合点进行拟合,获取疑似点的预测高程异常值。经过对比分析发现,34号点的真实值与预测值的差异较小,可认定为误判,对其进行留存,其余4个疑似点存在的误差均可作为粗差进行剔除。二者最终的结果比较如表2所示。

表2 IGrubbs与Grubbs粗差剔除效果对比Tab.2 Comparison of gross error elimination effect between IGrubbs and Grubbs

在实验过程中,Grubbs在置信水平为90.0%时仅识别出1个误差值,3个误差值未识别出;相比于Grubbs,IGrubbs在置信水平为95.0%或97.5%时能够较为准确地识别出4个误差值并进行剔除。在另外2种相同情况下,误差值的识别及判定效率均要优于Grubbs。在利用IGrubbs对训练样本数据进行预处理后,其剔除粗差前后的高程异常数据变化如图2所示。

由图2可知,在通过IGrubbs进行粗差探测及剔除时,发现参与后期建模的59个GNSS水准重合点中存在4个偏离正常值的数值,其中存在的粗差与正常值的最小差值为0.27 m。若未及时对其进行识别及剔除,将会严重影响后期所建拟合模型的预测精度。在对训练样本数据进行预处理后,测试重合点及检核点分布如图3所示。

图3 点位分布Fig.3 Distribution of points

2.2 构建拟合模型

在完成训练样本数据的粗差识别及剔除后,通过LWLR法来建立区域高程异常拟合模型。建模前,对实验数据进行归一化处理,可提高算法的计算效率。将模型中的参数k初始值设置为0.5,最大迭代次数为70,通过迭代计算完成研究区域内最适高程异常拟合模型的选择,并预测出检核点的高程异常值。在训练数据集及检核点预测数据的基础上,借助Matlab绘制出其相应的三维效果图(如图4所示)。为近一步比较分析拟合模型的预测精度,分别利用传统多面函数法、基于移去恢复法的二次曲面拟合来建立预测模型[19-20],对3种方法建模的预测结果进行了统计,其相应的残差值分布变化如图5所示。

图4 高程异常拟合三维图Fig.4 Three-dimensional graph of elevation anomaly fitting

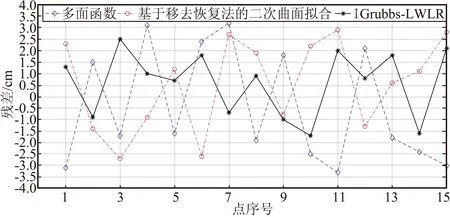
图5 模型检核点的残差对比Fig.5 Residual comparison of model checkpoints

由图5可以看出,传统多面函数法建模的检核点残差波动范围最为明显,稳定性相对较差;IGrubbs-LWLR所对应的残差值的最大值及最小值均要优于其他2种方法建立的拟合模型,变化更为趋近于0,拟合效果更为理想。为更加直观地了解各模型的拟合效果,选择外符合精度(检核点的均方根误差)作为模型精度的判定指标,具体如表3所示。

表3 不同拟合模型检核点的预测结果Tab.3 Prediction results of different fitting model checkpoints

由表3可知,多面函数法残差变化为-3.3～3.2 cm,基于移去恢复法的二次曲面拟合残差变化为-2.7～2.9 cm,IGrubbs-LWLR建模的拟合残差变化为-1.7～2.5 cm。相比之下,IGrubbs-LWLR的拟合残差变化区间较小,外符合精度为±1.6 cm,其拟合模型预测的精准度更高。表明针对小范围的地形起伏较为明显的区域,选用IGrubbs-LWLR来建立高程异常拟合模型具备一定的时效性及稳定性。

3 结论

为解决测量数据中粗差干扰及高程异常拟合模性构建方法选择的问题,本文提出利用IGrubbs-LWLR来完成区域高程异常拟合模型的建立,结论如下:

① 在常规Grubbs法则的基础上,引入自适应迭代及判定粗差提出工作完成的指标参数,降低了其原先易发生漏判及误判的概率,提高了该算法对样本数剧中粗差识别及判定剔除的效率;

② 在对数据预处理后,选用LWLR法来构建区域高程异常拟合预测模型,与传统多面函数法、基于移去恢复法的二次曲面拟合法相比,其精度分别提高了38.5%、23.8%。表明IGrubbs-LWLR应用于区域高程异常拟合模型的构建具备一定的现实性。

当前实验区域研究范围有限,地势变化较为简单,在之后的研究中,会将该方法应用于更为复杂多变的区域来构建拟合模型,同时也会对模型中的参数近一步优化提取,提高拟合模型的稳定性及时效性,为今后的测高工作提供更高的参考价值。