基于声比拟法的埋地输气管道泄漏数值模拟

陈一鸣,王 博,刘宏达,张秋实

(1.辽宁石油化工大学 石油天然气工程学院,辽宁 抚顺 113001; 2.中国石油天然气集团有限公司 长庆油田分公司第一输油处,陕西 西安 710021)

引 言

截至2018年底,我国油气管道总里程累计已达到13.6×104km,但其中已有半数以上的管道进入到了管道运行的“老龄期”[1],所以因腐蚀穿孔、疲劳失效等原因所造成的安全事故层出不穷。因此,实时对管道的运行状况进行检测,及时发现并准确定位泄漏点的位置,对保证输送管道的安全运行、保证人民的生命财产安全、降低经济损失,具有重大的现实意义。

国内外学者针对管道泄漏的检测与定位问题进行了大量的研究,Mansour等[2]针对输水管道的微小泄漏,运用CFD软件对泄漏过程进行了仿真模拟,得到了泄漏声源产生的机理;Xu等[3]对输气管道泄漏的声波场进行了研究,得到了泄漏声源的特征及变化规律;Lee等[4]运用大范围超声波传感器和欧几里德矢量机构建了油气管道智能失效预测系统;张卫国[5]基于负压波法,分析了不同泄露孔的泄露信号;常维宁[6]基于瞬变模型检测方法,对泄漏管道的瞬变流动规律进行了模拟和试验研究;顾明生[7]采用次声波信号分析法对供水管道泄漏现象进行了研究。虽然管道泄漏的检测方法有很多,但是每种方法都有各自的优缺点,周兆明等[8]阐述了负压波法、流量平衡法、次声波法、分布式光纤检测法和内检测技术等几种管道泄漏检测技术的概况,对比分析了不同泄漏检测技术的性能指标及优缺点。相比于其他方法,声波法具有定位精度高、响应时间短、适应能力强等优点,而输气管道泄漏声源的特性对声波法泄漏检测的精度和适应性起着决定性的作用。为此,本文运用声比拟法对不同泄漏口直径、不同管内压力以及不同泄漏时间的埋地输气管道泄漏声源的特性进行了仿真模拟,以便为管道泄漏声波检测法和定位系统的开发提供一定的理论依据。

1 数学模型

1.1 声比拟模型

声波法管道泄漏检测技术利用管道泄漏流体的气动噪声来检测和定位泄漏源[9]。由于噪声直接模拟法需要高精度数值求解方法及精细的网格结构,并且对于中、远场的求解较困难,因此未被广泛应用。而基于Lighthill的“噪声比拟”法可将波动方程与流动方程解耦,将求解结果作为噪声源,通过求解波动方程得到解析解,把流动的求解过程从声学分析中分离出来[10]。声比拟模型(Ffowcs Williams and Hawkings,FW-H)是基于Lighthill方法最常用的计算模型之一,其消耗的计算资源较小且无流场限制,因此选择该方法对埋地管道泄漏声场进行分析求解。

FW-H方程通过引入广义函数将Navier-Stokes方程按波动方程的形式重新整理而成[11],其方程可写为:

(1)

式中:α0为远场声速,m/s;p′为观测点声压,Pa;ρ为气体密度,kg/m3;ρ0为远场介质密度,kg/m3;t为时间,s;f为声源数据积分面;μi为i方向流体的速度分量,m/s;n为积分面法线方向;un、vn分别为积分面法线方向的流体速度分量和积分面移动速度分量,m/s;δ(f)为Dirac函数;H(f)为Heaviside函数;Pij、Tij分别为应力张量和Lighthill张量。

1.2 组分输运模型

当天然气管道发生泄漏时,泄漏气体浓度与周围气体浓度相互交换,该过程被称之为拟平衡过程[12],此过程遵循组分输运方程,控制方程如下:

(2)

(3)

式中:i为扩散介质种类;Yi为i介质的局部质量分数;Si为i介质质量分数源项;Ji为i介质质量扩散速率,kg/s;μt为湍流黏度,Pa·s;Sct为湍流施密特数;Dt为湍流扩散强度。

1.3 多孔介质模型

当埋地管道泄漏的高压气体扩散到土壤介质中时,流体因受到土壤的毛细阻力作用,湍动能量被不断削弱,直至渗漏到地表大气外。土壤介质可被看成是多孔介质,采用Fluent中定义的多孔介质模型对泄露气体在土壤内的扩散过程进行模拟。在已有动量方程中添加一个可用于计算动量耗散的源项S,该源项由两部分构成,即黏性损失项和惯性损失项[13],表达式如下:

(4)

式中:S为源项;μ为黏度,Pa·s;Dij、Cij为源项构成系数矩阵。

1.4 大涡模拟模型

输气管道泄漏的高速气体会在泄漏口附近产生湍动旋涡现象,为了准确地模拟管道的湍动流场,启用大涡模拟模型(Large eddy simulation,LES)。该模型通过对Navier-Stokes方程进行滤波运算,大于滤波宽度的大尺度涡运动进行直接模拟,而小于滤波宽度的小尺度涡运动通过亚格子尺度模型(Sub-grid scale,SGS)进行模拟。由于盒式滤波函数应用较广,因此采用盒式滤波函数[14]进行求解计算,其控制方程为:

(5)

式中:xt为任意网格节点的坐标;Δxt为第t方向滤波器网格尺度。

经滤波函数筛选后得到大尺度涡的Navier-Stokes方程如下:

(6)

(7)

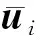
计算启动LES模型后,定义标准亚格子模型[15-16],模型控制方程如下:

(8)

(9)

(10)

(11)

(12)

(13)

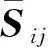
2 物理模型及边界条件

2.1 物理模型

选取天然气输送管道为研究对象,天然气是由多种气体混合而成,其中甲烷(CH4)占总体积分数的99.88 %,因此可选用CH4代替天然气混合物进行模拟计算。管道规格DN500,泄漏孔径5 mm,管道运行压力2 MPa;埋地管道顶部埋深1.2 m,土壤孔隙度0.267,渗透率3.846×10-5m2,土壤平均直径0.2 mm;物理模型如图1所示。

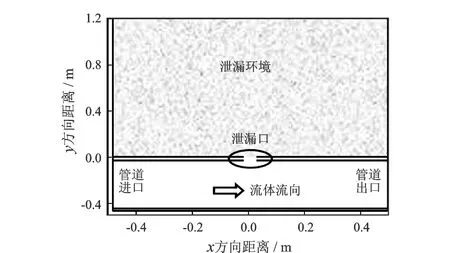
图1 物理模型Fig.1 Physical model

2.2 网格划分及边界设定

设定管道进、出口皆为Pressure边界,管道上、下壁面为标准无滑移壁面;土壤区域设定无反射边界条件,管道内壁面设定反射边界条件。采用结构化网格进行单元划分[18],局部位置进行加密处理以便于捕捉参数的变化。选取管道泄漏口流体的喷射速率为检验指标,对网格无关性进行验证,最终确定网格,如图2所示。

图2 网格划分及边界设定Fig.2 Mesh generation and boundary setting

3 埋地天然气管道声场模拟

3.1 埋地管道流场分析

当输气管道发生泄漏时,管内流动参数将会发生变化,泄漏口两侧临近区域的气体在压差的作用下向泄漏口处补充[19],致使泄漏点相邻区域内的气体密度减小、压力降低;由于管道内压的作用,使得更远处的气体向泄漏口相邻区间补充;以此模式从泄漏口处向管道上下游进行传播,从而形成声波震动的传播[20]。

为准确分析泄漏流场变化对声波传送造成的影响,首先对管道的泄漏进行流场分析。设定管道泄漏口直径为5 mm,管道内压为2 MPa。为清晰地观察泄漏口处管道内、外的速度分布特征,绘制管道泄漏口处速度变化曲线,如图3所示。

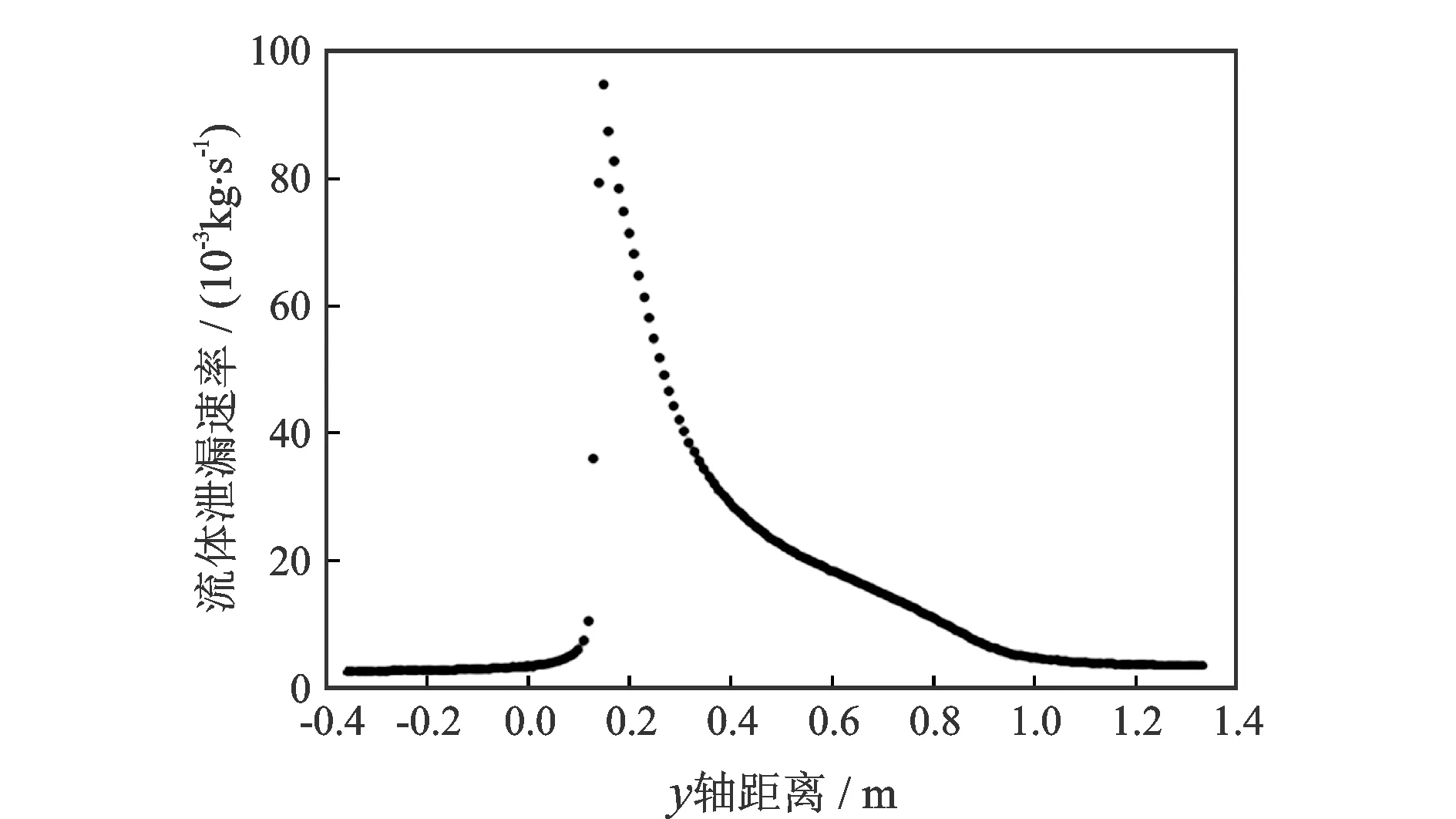
图3 泄漏口法向速度曲线图Fig.3 Normal velocity curve at leakage port

由图3可知,流体在泄漏口处(y=0.0 m)取得速度的最大值;在管道外部流体因受到土壤孔隙阻力的作用,其扩散速度逐渐递减,在管道上方0.2 m以后衰竭才较为明显, 且在地表附近的速度逐渐衰减至0 m/s。由此可见,管道外泄漏环境对流体的扩散会产生较大的影响。因此在测算各类泄漏检测装置时,应在真实的环境下进行试验,研究结果才能更好地服务于管道工程。

3.2 埋地管道声场分析

基于埋地管道流场分析的参数设置进行声场分析。图4为埋地管道泄漏气动噪声声源分布云图。

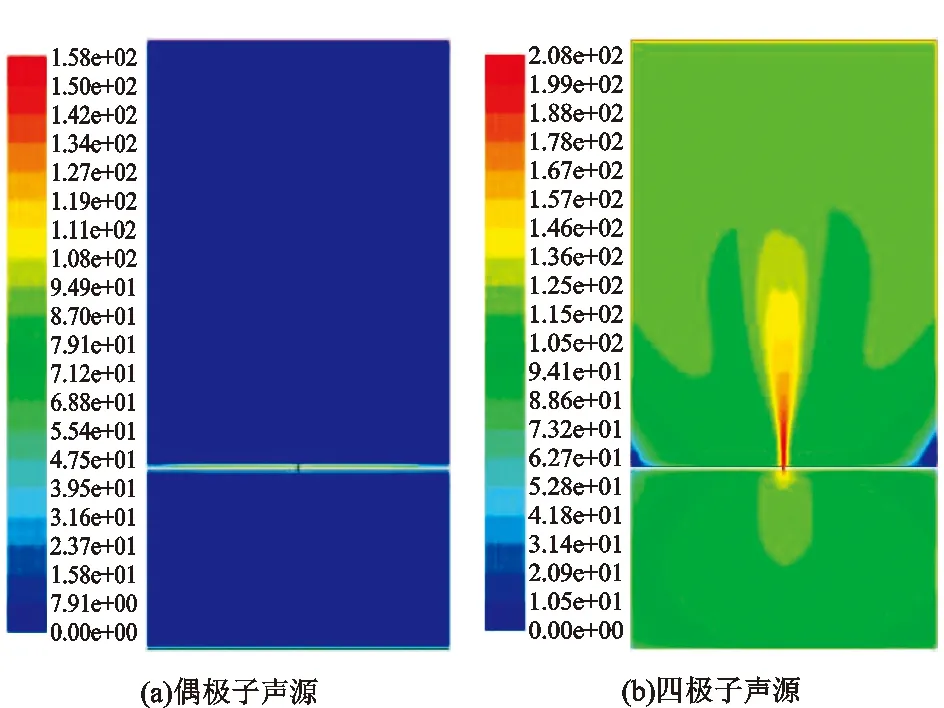
图4 管道泄漏气动噪声的声源分布云图Fig.4 Sound source distribution nephogram of pipeline leakage aerodynamic noise

由图4可知,在泄露口处气体喷射产生震动,从而形成四极子湍流噪声,因此四极子声源主要集中在管道以外的开扩区域,该声源也是管道泄漏噪声主要的声源。该结论与前人的研究结果一致[21-22]。

3.2.1 管道内压对管道泄漏声场的影响

为研究管道内压对泄漏声场的影响,设定管道泄漏口直径为5 mm,管道内压分别取2 MPa、3 MPa、4 MPa、5 MPa进行求解计算及泄漏声场分析。

图5为不同管道内压的四极子声源分布云图。

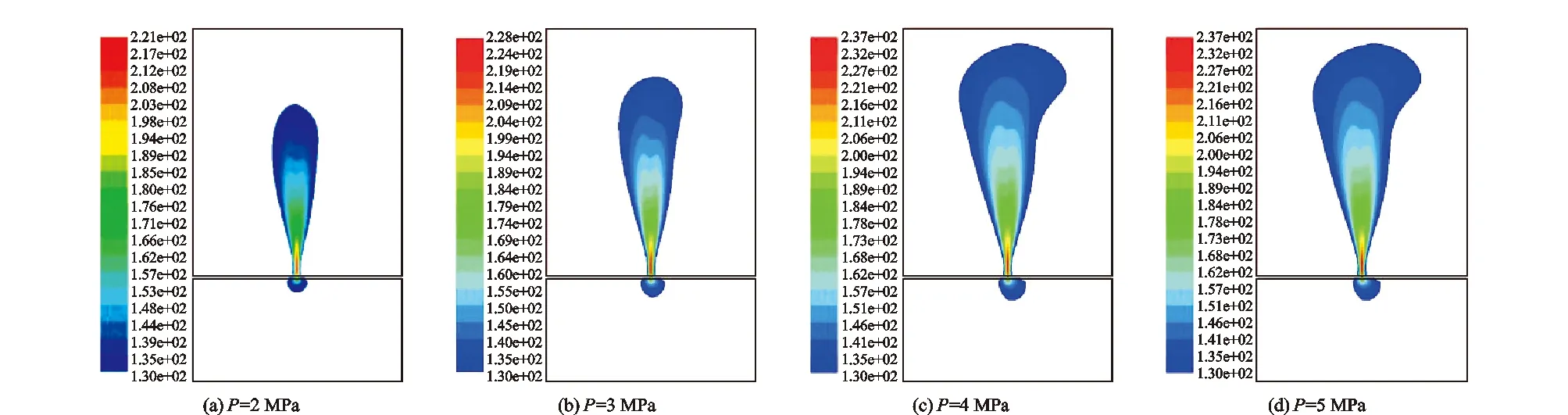
图5 四极子声源分布云图(声压大于130 dB)Fig.5 Quadrupole sound source distribution nephogram (sound pressure greater than 130 dB)

由图5可知,在泄漏口直径不变的条件下,随着管道内压的增加,四极子声源分布区域逐渐增大;但管道内部四极子声源的增幅远小于管道外部土壤区域内四极子声源的增幅,产生该现象的原因是管道内部泄漏声场是由于气体喷射的反作用力引起的涡流脉动,而管道外部泄漏声场是由于气体自身湍流脉动形成的涡流脉动,因此管道内压对管道外部的声场影响较大;当管道内压增加至一定程度时,泄漏声场逐渐趋于稳定。因此,在管道附近安装噪声传感器来检测管道泄漏情况是可行的。

图6为不同管道内压的偶极子声源变化曲线。

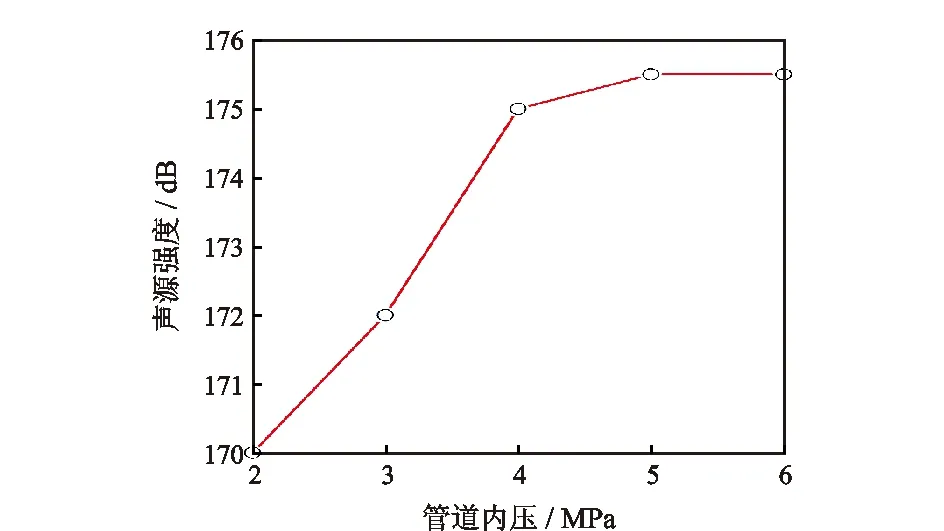
图6 不同内压的偶极子声源变化曲线Fig.6 Dipole sound source variation curve with pressure

由图6可知,随着管道内压的增加,泄漏声场的偶极子声源逐渐增大,但增幅程度很小且远小于四级子声源,这也进一步说明了管道泄漏的主要声源是四极子声源。

3.2.2 泄漏口直径对管道泄漏声场的影响

为研究泄漏口直径对埋地天然气管道泄漏声场的影响,设定管道内压为2 MPa,泄漏口直径分别取5 mm、10 mm、15 mm、20 mm进行求解计算及泄漏声场分析。

图7为不同泄漏口直径的四极子声源分布云图。由图7可知,在管道内压不变的条件下,不同管道泄漏口直径的四极子声源分布存在一定差异;在一定范围内,随着管道泄漏口直径的增加,泄漏声场的四极子声源的声波强度及影响区域逐渐增大,但当泄漏口直径超过一定数值后, 其分布规律基本保持不变,最大声源强度接近相同。这是因为泄漏初期随泄漏口直径的增加,管外天然气泄漏的流速逐渐增大,从而导致气动噪声的声波强度逐渐增加,当泄漏口直径进一步增大时,泄漏流体因受土壤孔隙阻力的作用,管道内外压差逐渐达到拟平衡状态,故管外声强增幅程度越来越小,最终趋于平稳;而管内流体经过上下两壁面反射后,声波相互叠加,使得管内局部声压增大,但仍低于管外声强。

图7 不同泄漏口直径的四极子声源分布云图Fig.7 Quadrupole sound source distribution nephograms under different leakage port diameters

图8为不同泄漏口直径的偶极子声源变化曲线。由图8可知,当管道泄漏口直径由5 mm增至20 mm后,偶极子声源强度基本稳定在173 dB左右,其平均增长速度为0.47 dB/mm,因此可知虽然偶极子声强随着泄漏口直径的增加有所增大,但因受泄漏口两侧流体的壁面剪切力作用,其增加幅度较小。

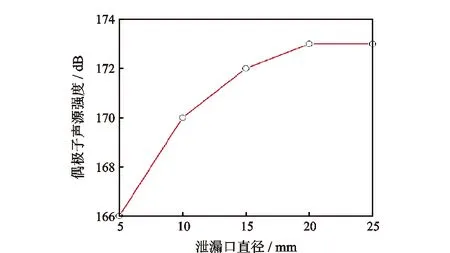
图8 不同泄漏口直径的偶极子声源变化曲线Fig.8 Dipole sound source variation curve with leakage port diameter

3.2.3 不同泄漏时间对管道泄漏声场的影响

为了研究泄漏声场随泄漏时间变化的发展规律,设定管道内压为2 MPa,泄漏口直径为5 mm进行模拟计算。

图9为不同泄漏时间的四极子声源分布云图。由图9可知,随着泄漏时间的延长,流体湍流脉动流场的四极子声源不断发展,但很快达到拟稳定状态;当泄漏发生0.08 s后,四极子声源分布基本趋于稳定,这主要是因为在既定的压力及泄漏口直径的条件下,流体流场已经达到拟稳定状态,流场内参数不再变化,这也说明泄漏声波强度与管道内压、泄漏口直径有一定的内在联系。

图9 不同泄漏时间的四极子声源分布云图Fig.9 Quadrupole sound source distribution nephograms at different leakage times

图10为不同泄漏时间的偶极子声强曲线图。由图10可知,泄漏声场偶极子声源的最大声强随泄漏时间的延长逐渐减小,但很快趋于平稳;当泄漏时间达到0.08 s后,偶极子最大声强数值基本保持不变,这主要是受流场稳定性的影响,泄漏初期管道内外压差较大,流体的湍流脉动较剧烈;随着泄漏时间的延长,泄漏流场逐步达到拟稳定状态,各项参数快速趋于稳定,因此声波强度也不再变化。

图10 不同泄漏时间的偶极子声源变化曲线Fig.10 Dipole sound source variation curve with leakage time

4 结 论

(1)埋地管道发生泄漏后,管内流体的速度分布较为均匀,而管外土壤中泄漏流体的速度变化梯度较大。

(2)埋地管道泄漏声源由偶极子声源和四极子声源构成,其中偶极子噪声主要集中在管道壁面处,而四极子噪声主要集中在管道外的开阔区域。

(3)随着埋地管道内压的增加,泄漏声场的声强逐渐增大;随着泄漏口直径的增加,泄漏声场的声强也逐渐增大,但泄漏口直径变化引起的声强变化程度远小于内压变化引起的声强变化程度。