基于非线性模型预测的欠驱动船舶轨迹跟踪控制研究

杜 朋 柱, 张 砚 北, 隆 武 强, 朱 晶 宇

(大连理工大学 能源与动力学院,辽宁 大连 116024 )

0 引 言

船舶轨迹跟踪控制是指船舶在规定时限内跟踪上期望的路径,并一直保持跟踪状态的控制[1],该问题一直以来都是智能化船舶技术领域的研究热点.大多数船舶是欠驱动控制的,只有螺旋桨产生的纵向推进力和舵产生的艏摇方向转船力,而横荡方向没有控制力[2],其控制系统具有非线性、大惯性、时滞、局部线性不可控等特点[3].海上运行的船舶不可避免受到外界环境干扰,具有高度非线性和强耦合特性[4],所以在环境干扰下的稳定控制是船舶轨迹跟踪控制的关键.在模型不确定性和外部扰动的影响下,船舶运动控制的鲁棒性会受到影响[5].因此,为实现船舶高可靠性的自主航行,良好的运动控制系统的研究与设计具有重要意义.

Fossen等[6]利用基于视距的PID控制方法实现船舶路径跟踪,该方法是目前应用最广泛的船舶运动控制策略.但由于船舶在实际运行中存在不确定参数摄动以及外界环境干扰等问题,该控制策略的路径跟踪偏差较大.Do[2]在欠驱动船舶路径跟踪问题中引入弱非线性Lyapunov函数和强非线性Lyapunov函数,克服了欠驱动带来的模型不确定性.张晓玲等[7]以三自由度全驱动船舶为研究对象,针对轨迹跟踪控制中船舶遭受未知外部环境扰动的问题,设计了一种带扰动观测器的自适应动态面滑模控制方法,并进行了仿真试验,验证了所设计控制律的有效性.施文煜等[8]以某散货船为研究对象,基于欠驱动船舶的误差模型,采用Lyapunov直接法设计虚拟控制量,结合反步思想和积分滑模控制方法,得到纵向推力及转艏力矩滑模控制律,仿真结果显示,该轨迹跟踪控制策略具有较好的跟踪性能.焦建芳等[9]引入具有约束作用的性能函数进行控制器的设计,通过径向基函数(RBF)神经网络克服模型参数摄动,利用非线性增益函数与双曲正切函数设计自适应律,对外界未知干扰与模型参数逼近误差的总和的界进行估计,仿真试验表明,该船舶轨迹跟踪误差收敛到规定的范围内,验证了所提控制策略的有效性与优越性.

船舶运动数学模型主要有[10]整体型数学模型(Abkowitz模型)、分离型数学模型(ship manoeuvring mathematical model group,MMG)和响应型数学模型(Nomoto模型).现阶段绝大多数船舶运动控制都是基于以上机理模型进行设计的.其中,应用较为广泛的是由Fossen[11]整理推导的欠驱动三自由度整体型平面运动数学模型,因此本文将以此模型为基础进行轨迹跟踪控制研究设计.

基于以上研究成果,本文针对欠驱动船舶轨迹跟踪控制的非线性特点,在考虑外界环境干扰的情况下,结合扩展卡尔曼滤波器和序列二次规划(sequential quadratic programming,SQP)算法,设计基于非线性模型预测的船舶轨迹跟踪控制策略,并基于一艘运输船进行仿真试验,验证所设计轨迹跟踪控制器的有效性和实时性.

1 船舶欠驱动运动数学模型

研究船舶平面运动控制时,只考虑船舶纵荡、横荡和艏摇这3个自由度,如图1所示.

图1 船舶三自由度平面运动

船舶三自由度的运动由状态量η=(xyψ)T和ν=(uvr)T描述.位置状态量η表示为船舶在水平面的横坐标、纵坐标和艏摇角.速度状态量ν表示为船舶的纵荡速度、横荡速度和艏摇角速度.三自由度船舶运动数学模型的表达式[12]如下:

(1)

其中,矩阵J(η)、M、C(v)和D分别为

船舶的推进力和力矩控制量τ=(τu0τr)T.其中τu表示船舶纵向推进力,τr表示偏航力矩,一般纵向推进力由船舶的螺旋桨产生,偏航力矩由船舶的舵或以差速控制的双螺旋桨产生.环境干扰量τe=(τue0τre)T,其中τue与τre分别为环境干扰作用在纵向和艏摇方向的外界扰动力及干扰力矩.最终式(1)的船舶运动学和动力学方程可表示为

(2)

上述模型即典型的船舶欠驱动三自由度平面运动模型,该模型已经被广泛地应用在船舶运动控制研究中,因为该模型参数较少,计算量适中,拟合度高,在船舶运动控制中具有很大优势.

2 非线性模型预测轨迹跟踪控制器设计

船舶非线性轨迹跟踪控制问题可以转化为有限时域内的非线性约束优化问题,而序列二次规划算法是求解该问题的有效方法.这一方法具有超线性收敛速度,在轨迹跟踪控制问题中具有实时应用的潜力.

本文对应用非线性模型预测解决水面船舶轨迹跟踪控制问题的有效性及实时性进行研究,设计具有一定复杂度的参考轨迹,可以对船舶在高速直线、低速曲线、不同回转半径、非光滑参考路径等工况下的轨迹跟踪情况进行测试,并能很好地反映船舶的工况切换情况.控制器架构如图2所示.

图2 非线性模型预测轨迹跟踪控制器架构

2.1 预测模型设计

将式(2)欠驱动三自由度平面运动模型作为预测模型,其一般形式为

(3)

2.2 目标函数设计

为了使船舶快速且平稳地跟踪到参考轨迹,将目标函数定义为

RΔU(k+i-1|k)+ρε2

(4)

该目标函数的第一项对系统输出量偏差进行限制,反映了控制器对参考轨迹的跟踪能力.第二项考虑了控制量的增量,以避免控制量突变.权重矩阵用以调节轨迹跟踪性能与船舶操纵性能.同时,在目标函数中引入松弛因子以防止优化问题求解过程中出现没有可行解的情况.

2.3 约束条件设计

考虑控制过程中的控制量约束Umin、Umax,船舶的推进力与偏航力矩及其在一个采样周期内的增量约束ΔUmin、ΔUmax,约束条件可表示为

(5)

综上所述,船舶非线性轨迹跟踪控制问题可以转化为有限时域内的最优化问题:

(6)

2.4 控制目标设定

本文的控制目标设定如下:在给定参考轨迹(xryrψr)T的情况下,通过求解优化问题(6),得到船舶的控制量(τuτr)T以跟踪到设计的轨迹及船舶平面位姿.使X轴位置偏差xe=xr-x=0与Y轴位置偏差ye=yr-y=0以跟踪到船舶目标速度,使艏摇角偏差ψe=ψr-ψ=0以控制船舶平面位姿.

3 轨迹跟踪控制仿真验证

为了验证所提非线性模型预测在船舶轨迹跟踪控制中的可应用性,本文基于Simulink平台搭建了非线性模型预测轨迹跟踪控制仿真模型,包括参考轨迹、轨迹跟踪控制器、船舶模型与可视化模块,整体架构如图3所示.为了提高非线性模型预测的跟踪控制效果,对参考轨迹进行了预览处理,其输出为以时间为序列的Np×3位置坐标矩阵,即轨迹向量组合得到的矩阵.轨迹跟踪控制器是基于扩展卡尔曼滤波器的非线性模型预测控制器.船舶模型包括了三自由度欠驱动船舶运动控制模型与相应的环境干扰模型.

图3 非线性模型预测轨迹跟踪控制仿真模型架构

3.1 参考轨迹的设计

参考Karetnikov等[13]设计的拉多加水域模拟路线,同时考虑到船舶的可操作性,设计了具有一定复杂度的参考轨迹,如图4所示.该轨迹设计了船舶起动航道(L1)、不同速度工况下的5条直线航道(L2、L4、L6、L8、L10)和4条圆形航道(L3、L5、L7、L9),同时设计圆形航道沿路线对回转半径进行递减.

图4 参考轨迹

参考轨迹航道参数见表1.

表1 参考轨迹航道参数

3.2 船舶及环境干扰设计

为了验证所设计的非线性模型预测轨迹跟踪控制方案的有效性,采用Do等[14]提供的运输船作为控制对象,该船长为38 m,质量为118×103kg.

Do通过VERES软件计算船舶的水动力导数,可以得到运输船的惯性参数矩阵的分量和阻尼参数矩阵的分量分别为

m11=120×103kg,m22=217.9×103kg,

m33=636×105kg·m2,

d11=215×102kg/s,d22=117×103kg/s,

d33=802×104kg·m2/s

将上述惯性参数矩阵的分量和阻尼参数矩阵的分量代入式(1),便可以得到控制对象船舶的欠驱动运动数学模型.

为了模拟船舶在真实运行条件下的环境情况,设置外界的风浪干扰作用力及力矩如式(7)、(8)所示,其随时间的变化曲线如图5所示.

图5 风浪干扰作用力及力矩模拟

(7)

(8)

3.3 仿真结果

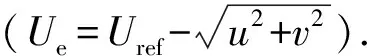
图6 路径跟踪结果

(a) 位置和方向跟踪误差

(a) 推进力

从图6路径跟踪结果可以看出,使用非线性模型预测轨迹跟踪控制器可以很好地跟踪到目标航道路径,实际路径与参考路径基本没有偏移.

轨迹跟踪误差结果和控制量及各状态量曲线(图7、8)展示了船舶在各航道变换中的工况切换情况.在具有初始纵荡速度偏差ue与艏摇角偏差ψe的情况下,非线性模型预测轨迹跟踪控制器对推进力τu和偏航力矩τr进行了快速规划,船舶合速度和航向在10 s内调整并稳定到设计参考值.

在所设计的非光滑参考轨迹(起动航道L1～直线航道L2)中,设计速度由3 m/s转换为10 m/s,设计艏摇角由π/4转换为0,船舶在20 s内达到了直线航道的设计航速与艏摇角.最大X轴位置跟踪偏差为15.36 m,仅为船长的40%.但是,对控制量曲线进行分析后发现,规划得到的推进力τu和偏航力矩τr的变化率过大,不符合船舶实际操控要求,因此在对非线性模型预测轨迹跟踪控制器的设计中,需要对控制量变化率进行更加合理的约束限制.

在各高速工况直线航道(L2、L4、L6、L8、L10)中,除工况切换时出现较小的超调量以外,船舶轨迹跟踪效果较好,在较短时间内(约10 s)跟踪到设计航道位置及航速.

船舶进入具有较低速度限制的半圆形回转航道(L3、L5、L7、L9)后,快速进行了减速操作(推进力τu转换为负值),X、Y轴位置跟踪偏差呈周期性波动,即呈现正负交替的偏差图,船舶在跟踪具有减速工况的回转航道时,会运行在参考半圆轨迹的外侧.

X轴位置跟踪偏差在光滑参考路径(L2～L10)下整体小于3 m,小于船长的10%,满足船舶的应用要求.同样,Y轴位置跟踪偏差在光滑参考路径下整体小于3.5 m,小于船长的10%.

从以上分析中可以看出,非线性模型预测在轨迹跟踪应用中展现了良好的控制效果,具有快速响应、跟踪误差小的特点.

4 结 语

船舶非线性轨迹跟踪控制问题可以转化为有限时域内的非线性约束优化问题,结合扩展卡尔曼滤波器和序列二次规划算法,本文设计了基于非线性模型预测的船舶轨迹跟踪控制策略.仿真结果表明,使用非线性模型预测轨迹跟踪控制器可以较好地跟踪到目标航道路径.在具有初始纵荡速度偏差与艏摇角偏差的情况下,船舶合速度和航向能够得到快速调整.但船舶在对非光滑轨迹进行跟踪时容易出现控制量剧烈变化的现象,不符合工程应用要求.在参考轨迹为光滑的直线航道及回转航道时,船舶轨迹跟踪效果较好,满足船舶的操控要求.非线性模型预测在船舶复杂工况切换下的轨迹跟踪控制中表现出较好的鲁棒性,具有实际应用前景.