斜流式气波制冷机制冷性能数值模拟研究

胡 大 鹏, 白 宇, 刘 凤 霞*

(1.大连理工大学 化工学院,辽宁 大连 116024;2.大连理工大学 精细化工国家重点实验室 智能材料化工前沿科学中心,辽宁 大连 116024 )

0 引 言

天然气作为一种清洁高效的能源[1],其加工处理工艺中需要降温使天然气中的水汽冷凝分离,并回收其中的轻烃等有效成分[2-3].针对上述需求,大连理工大学成功研发出气波制冷机[4-5],通过振荡管内非定常波系运动实现能量的交换,达到制冷目的,并针对不同操作和结构参数做了诸多研究[6-10].气波制冷机可以充分利用天然气层中的压力能,其等熵效率高于节流阀,同时相比膨胀机转速较低,且具有一定持液运行能力,十分适用于天然气处理.

传统的双开口气波制冷机为轴流式结构,调整波转子通道与旋转轴夹角,则可为气体流动带来一定的离心力,可以用于克服制冷循环过程中的流动阻力,并输出具有更高压力能的低温气体,提高等熵效率;若用于过膨胀循环方式,可以减小甚至代替外置循环设备,使得整体结构更加紧凑,减少空间占用,节约设备和配管成本.同时在给定转速下调整合适锥角,可以改变大端旋转线速度,有利于降低渐开渐闭损失和黏性损失.谢明明[11]、袁博[12]对径流式波转子进行了研究,其带来循环压差的同时轴功大幅上升,且制冷效果受到很大影响,同时其结构上的不稳定性制约了实验和实际应用.

本文综合轴流式和径流式气波制冷机的优点,提出一种斜流式气波制冷机,构建锥形波转子理想波图,完成端口匹配,建立并简化模型,进行数值计算,研究锥角、压比、转速对于制冷和增压效果的影响,并与轴流式和径流式气波制冷机加以对比.

1 斜流式气波制冷机理论及模型建立

本文提出的斜流式气波制冷机,其核心部件波转子为锥形结构,振荡管为等截面直通道,如图1所示.进气方式为返流式,低温出口位于大端一侧,低压入口位于小端一侧,从而能够利用锥形结构产生的离心力.

图1 直通道锥形波转子三维结构示意图

1.1 理想波图构建及端口匹配

为实现气波制冷,波转子振荡管内需合理控制运动波系[13-15].依据气体动力学原理并借鉴轴流式气波制冷机理想波图(图2),得到如图3所示的斜流式气波制冷机理想波图.

图2 轴流式气波制冷机理想波图

在一个周期内,制冷过程大致可分为高压排气阶段和低温排气阶段.

(1)高压排气阶段

振荡管匀速旋转,当高压入口与振荡管接通,向通道内传递一个右行激波S1,气体压力增大、温度升高.

当右行激波S1传播到通道右侧时,接通中压出口,发生开口反射形成左行膨胀波E1.

波转子继续旋转,高压入口关闭产生右行膨胀波E2,中压出口在E2到达振荡管右端时闭合.

(2)低温排气阶段

由于通道右侧压力低于中压出口压力,中压气体在波转子通道内膨胀,在通道尾部形成激波S2.

本文根据Hu等的研究设计方法[16],按表1操作参数设计锥形波转子结构参数,见表2.

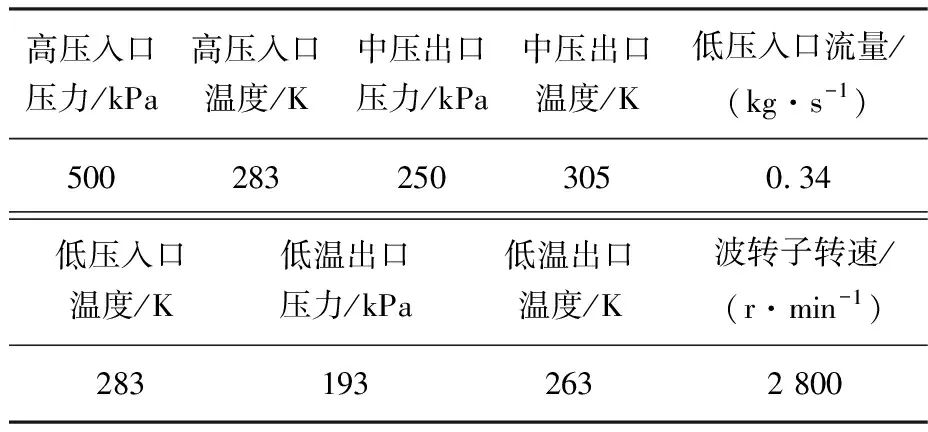
表1 斜流式气波制冷机典型工况操作参数

表2 锥形波转子结构参数

1.2 计算模型及数值方法

依据已构建的理想波图,为更直观地展现斜流式气波制冷机内部气体流动状态,综合考虑准确性和计算量,将波转子结构由三维向二维简化[17-18],类比轴流式和径流式气波制冷机二维展开方式,按照圆台展开方式展开:锥形波转子两条母线延长相交,得到新的圆心;选取内外弧长等于原锥形波转子两端周长,如图4所示.

图4 三维向二维转换示意图

利用Gambit软件进行网格划分,采用结构化网格,经过网格无关性验证,全局网格尺寸为2 mm×2 mm,网格数共计87 970,通道两侧设为周期性边界,得到如图5所示网格模型.利用流体仿真软件Ansys Fluent进行数值计算.介质选用理想空气;计算类型为基于密度的瞬态计算;湍流模型设置为Realizablek-ε模型;离散格式设置为AUSM+二阶迎风格式[19-21];时间步长设置为1×10-5s,迭代次数为20.

图5 二维网格模型示意图

如图6所示,对比Okamoto等的实验数据发现[22],虽然由于管壁非绝热以及黏性损失等原因出现细微差距,但静压变化规律与实验数据整体吻合,说明本文采用的计算模型可用于描述波转子通道内部气体流动状态,误差在可接受范围内.

1.3 性能评价指标选取

(1)制冷效果

等熵效率(η)定义为气波制冷机进出口的实际焓降与等熵焓降之比:

(1)

式中:ΔHpr为单位时间气波制冷机进出口的实际焓降,J/s;ΔHid为单位时间理想焓降(等熵焓降),J/s.鉴于本文外循环气波制冷机的工况,进口为高压入口,出口为低温出口,气体经过斜流式气波制冷机的热力学焓的实际变化量

ΔHpr=mcp(Thp-Tlt)

(2)

式中:m为质量流量,kg/s;cp为比定压热容,J/(kg·K);Thp为高压入口温度,K;Tlt为低温出口温度,K.

根据气体等熵变化计算式,可得气体膨胀的理想焓降为

(3)

则等熵效率计算式可以表示为

(4)

(2)增压效果

本文定义循环压差为低压入口和低温出口气体总压差,用来衡量斜流式气波制冷机的气体增压效果.

2 数值模拟与分析

2.1 锥角对波转子性能影响

为了对比在同样操作参数下波转子锥角对气波制冷机制冷性能和增压效果的影响,在表1所列工况下,保持波转子小端中径、振荡管长不变,端口尺寸、固壁面尺寸、高中压端口尺寸和相对位置均不变,分别建立锥角α为0°(轴流式)、6°、12°、20°、30°、45°、60°、90°(径流式)的单周期等截面直通道结构波转子.

锥形波转子随锥角增大,内外径差值Δr增大,mω2Δr增大,产生更大的离心力,可以用来克服循环阻力,并输出具有更高压力能的低温气体.由图7可得出,低压入口进气压力下降,回气所需压力降低;低温出口出气压力上升,气体在波转子中膨胀输出的低温气体压力提高.

图7 不同锥角下波转子增压性能

由于所建立模型在改变波转子锥角时保证各端口所占角度不变,且角速度不变,原则上振荡管与端口接通时间相同,但实际由图8可看出,锥角增大气波制冷机气体流量明显减小,相对于锥角0°(轴流式)波转子,12°锥形波转子高压入口进气流量下降约15%,至90°(径流式)时,流量降低近30%.这是由于高压入口位于大端,高压气运行方向与离心力相逆,随锥角增大,离心力使进气阻力增大.

图8 不同锥角下波转子轴功和气体流量

循环推动力的来源是锥形波转子的离心力,其增大必然会带来轴功消耗的增大,但同时流量下降一定程度上会减缓轴功上升.由图8可以看出,锥角较小时,流量下降较快,轴功上升较慢,锥角为12°时,轴功仅增大1.26 kW;锥角较大时,流量下降趋缓,轴功上升迅速,至锥角为90°(径流式)时,轴功上升至14.3 kW,此时所需电机功率增大,能耗提高,经济性下降.

锥形波转子两侧线速度不同,导致高压入口进气状态发生改变.因为振荡管有一定宽度,在旋转至高压端口时并不能瞬时接通和关闭,流动状态和速度分布如图9所示,轴流式波转子渐开渐闭现象使得进气初期,入射流股会在上下管壁间多次碰撞,带来很大的流动损失;而随锥角增大,波转子高压侧线速度增大,12°时外圈线速度由43.1 m/s增大至64.9 m/s,振荡管达到完全接通状态的时间减少,渐开渐闭损失降低,入射流股反射碰撞程度降低,气体流动损失下降,流速提高;当锥角进一步增大,60°时外圈线速度增大至133.0 m/s,径流式增大至145.7 m/s.此时高压进气入射后快速流向压力面并附壁,再缓慢向通道内扩散.入射流股在压力面汇聚并压缩,通道实际流通面积减小,产生节流损失.接触面扭曲程度严重,黏性耗散、掺混等流动损失更为严重.

(a) 0°锥角(轴流式)

波转子锥角改变反映在振荡管内的温度分布如图10所示,与轴流式波转子相比,以12°为代表的小角度锥形波转子分界面运动距离增大,气体膨胀深度提高,制冷温降增大;而对于大角度锥形波转子,进气流量下降,流动损失增大,加之离心力对入射气体做功抑制其膨胀,导致分界面运动距离减小,膨胀深度降低,制冷温降减小.

(a) 0°锥角(轴流式)

由图11(a)可以看出,当锥角较小时,随锥角增大,气波制冷机制冷温降(Thp-Tlt)增大,同时低温出口气体压力增大,由式(4)可得等熵效率η提升,气体膨胀制冷效果提高;当锥角较大时,虽然低温出口气体压力持续上升,但制冷温降大幅下降,制冷效果快速恶化.锥形波转子制冷效果随锥角先增大后减小.为进一步得到精确最优值,在6°～12°及其附近,每隔2°设置一个计算点,如图11(b)所示,在12°存在一个最优锥角.此时制冷温降和等熵效率相较轴流式分别高9.59 ℃和13.8%,相较径流式分别高20.48 ℃和30.9%.

(a) 0°～90°锥角

2.2 转速对锥形波转子性能影响

本节固定12°锥角,保持其余结构参数和工况不变,转速由1 800 r/min逐渐增大至4 400 r/min.

提高转速是在内外径差值Δr不变的情况下,通过增大角速度ω,产生更大的离心力.由图12可得,随转速由1 800 r/min增大至4 400 r/min,离心效果增强,轴功增大;循环压差总体上呈上升趋势,其在转速低于2 500 r/min时较低,由于激波在固壁面发生反射,使得管内整体压力提升,低压回气阻力提升.

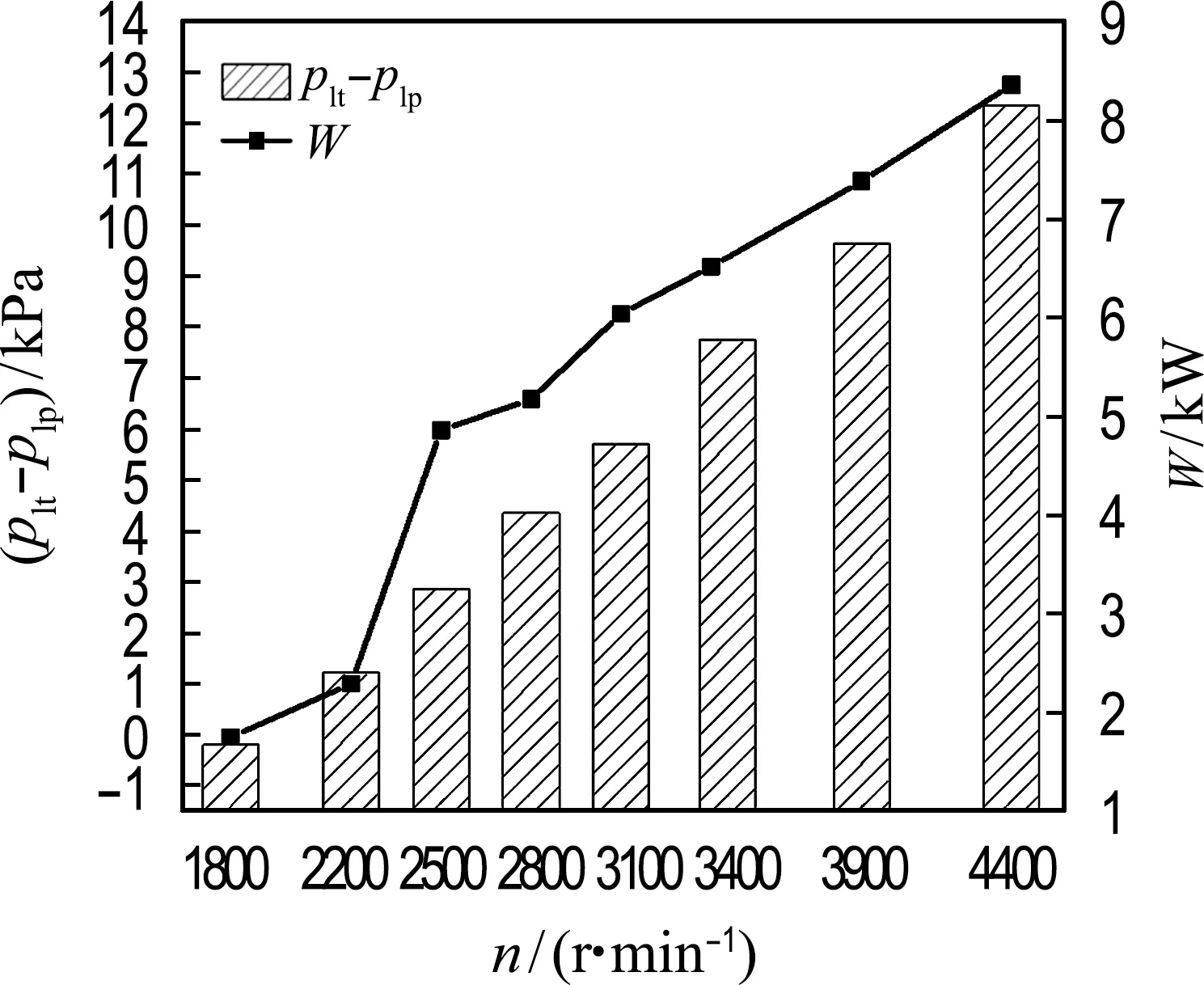
图12 不同转速下波转子增压性能

如图13所示,制冷温降和等熵效率先上升后下降,在2 500 r/min处达到最高.在转速低于最优转速时,激波到达振荡管末端时,中压出口尚未接通,激波发生固壁反射,重新加热低温气体,导致制冷效果下降;而转速高于最优转速时,中压出口提前接通,此时激波尚未到达,振荡管末端气体压力较低,中压出口会入射一道压缩波,同样会影响制冷效果.

图13 不同转速下波转子制冷性能

2.3 压比对锥形波转子性能影响

本节仍取锥角12°,固定低温出口气体压力193 kPa,从300 kPa至700 kPa调整高压入口气体压力,对应压比从1.5至3.5变化.

如图14所示,随着压比增大,高压入口进气流量增大,相匹配的低温出口出气流量也随之增大,推动气体排出所需的回气压力随之增大,循环压差降低.由于锥形波转子运行带来离心力,轴功相应更大,循环压差相比轴流式波转子平均高4.5 kPa,流量较低时,锥形波转子的循环压差会大幅降低,但仍高于轴流式波转子.

图14 不同压比下波转子增压性能

如图15所示,压比提高带来的进气流量增大,使得接触面移动距离变长,气体膨胀深度增大,制冷温降增大,流动损失所占比例降低,等熵效率提高.由图15可以看出,相比轴流式波转子,锥形波转子等熵效率提升15%以上,同时制冷温降提高约30%.

图15 不同压比下波转子制冷性能

3 结 论

(1)在固定工况的情况下,斜流式气波制冷机增压性能介于轴流式和径流式之间,同时制冷效果优于二者.随锥角增大,循环压差和轴功一直增大,制冷温降和等熵效率先增大后降低,在锥角12°左右达到最大.因而适当锥角的斜流式气波制冷机增压效果优于轴流式,且轴功小于径流式,同时制冷效果均大幅优于二者.

(2)转速的提高会直接增大离心效果,带来循环压差和轴功消耗的增大;但制冷温降和等熵效率会先上升后下降,转速在2 500 r/min时达到制冷效果的峰值.

(3)压比的增大会带来气波制冷机气体流量的增大,轴功消耗会上升,循环压差降低.同时压比增大,流动损失占比下降,制冷效果有所提升.在同等工况下,斜流式气波制冷机循环压差平均高于轴流式4.5 kPa,制冷温降提高约30%,等熵效率提升15%以上.