适用于区块链溯源场景的门限签名方案

李 莉，李 涛，杜慧娜

(东北林业大学 信息与计算机工程学院，黑龙江 哈尔滨 150040)

0 引 言

随着区块链技术[1]的快速发展，区块链溯源技术得到了广泛的应用。然而，在区块链溯源系统中，传统的群签名、环签名和代理签名等签名算法并不适用。

目前对数字签名的研究主要集中在基于公钥密码体制。文献[2]和文献[3]研究了区块链系统中的门限ECDSA方案，两种门限ECDSA方案都无需可信中心参与。Schnorr提出了Schnorr签名方案[4]，相比较ECDSA签名算法明显缩短了签名长度，文献[5，6]提出了两种基于Schnorr签名的门限签名协议，但是未应用于区块链场景中。文献[7-9]所提签名方案，需可信第三方进行密钥分配。文献[10]提出了基于Asmuth-Bloom秘密共享的签名方案，允许签名成员加入和退出，但是签名验证效率较低。文献[11]提出了基于Pedersen承诺和Schnorr协议的安全多方计算协议，然而恶意节点可通过合谋攻击获取用户的私钥，从而导致签名信息的可信度受到威胁。文献[12]所提出的门限RSA签名方案，允许节点的动态加入，但没有考虑节点退出问题。以上方案适配于区块链溯源场景时具有一定的效率问题和安全性问题。

针对上述问题，本文基于Schnorr门限签名算法和Pedersen可验证秘密共享方案，提出了一种适用于区块链溯源系统的门限签名方案。该方案摒弃了依赖可信中心的设计，而是通过节点之间的相互协作来生成子密钥并进行签名生成，设计了符合区块链溯源场景的成员加入和成员退出机制。本文方案在缩短签名时间和签名验证时间的同时，可以有效地预防抗合谋攻击和签名伪造。

1 预备知识

1.1 Schnorr签名算法

Schnorr数字签名算法的安全性基于离散对数的困难性[13]，此外，该算法大部分计算可以在签名前的预处理阶段完成。其具体方案定义如下：

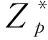
(2)签名算法：设待签名的消息为m，签名者选择随机数k∈Zq， 计算e=gkmodp，r=H(m‖e)，s=k+xrmodq， 则得到对消息m的数字签名 (r，s)。

(3)签名算法验证：签名验证者收到签名 (r，s，m) 后首先计算e′=gsy-rmodp， 然后验证等式r=H(m‖e′) 是否成立，若成立则签名有效。

1.2 Pedersen可验证秘密共享

秘密共享[14]的提出是为了解决密钥管理的安全问题。Shamir提出的基于拉格朗日插值多项式的 (t，n) 门限方案中n为成员个数，t(t≤n) 为阈值。秘密被分享为n个子密钥分发给n个成员，只有不少于t个子密钥才能恢复秘密。Pedersen可验证秘密共享方案是将承诺方案与Shamir方案[15]相结合。假设有n个成员 {P1，P2，…，Pn}， 要共享的秘密为s，p为一个大质数。q为p-1的一个大质数因子，选取阶数为p生成元为g的循环群G。Pedersen方案具体过程描述如下：

(1)秘密分发阶段：秘密分发者D在Zq上随机选择n个非零元素x1，x2，…，xn构造两个t-1阶多项式

f(x)=a0+a1x+a2x2+…+at-1xt-1

(1)

g(x)=b0+b1x+b2x2+…+bt-1xt-1

(2)

其中，f(0)=a0=s。 然后分发者D计算每个子密钥si=(f(xi)，g(xi))， 将si作为Pi的秘密份额。同时分发者计算并广播承诺Cj=gajhbj，j=0，…，k-1。 每个参与者Pi在收到自己的子密钥后判断等式(3)是否成立，若成立则说明子密钥有效

(3)

(2)秘密恢复阶段：秘密恢复者根据拉格朗日插值多项式的存在唯一性定理，通过t个 (xi，f(xi)) 可以确定唯一的t-1阶多项式f(x)， 以此来进行秘密恢复，得到秘密s=f(0)

(4)

2 本文方案

2.1 安全目标定义

本文提出的适用于区块链溯源系统的Schnorr门限签名方案由n个成员 {U1，U2，…，Un} 组成，在区块链系统中n个成员通过安全的点对点通道以及广播通道进行通信。假设门限签名方案中的阈值为t，签名者集合为T∈{U1，U2，…，Un}，|T|=t。 具体的安全目标如下：

(1)实现完全去中心化。整个方案不需要借助第三方可信机构进行密钥生成和密钥管理，而是由成员之间通过安全通信通道交互完成密钥生成、密钥分发和数字签名等协议。

(2)数字签名的不可伪造性。在区块链溯源系统中对于已经上链的商品溯源信息，任何恶意节点都不能伪造合法节点所生成的签名信息。

(3)抗合谋攻击。当成员人数少于门限值t时，无法生成门限签名，只有当至少t个成员共同参与时，才能生成有效的门限签名。本文方案允许恶意敌手A可以腐败的成员个数最大为t-1。 保证在少于t个成员的私钥泄露时，签名者对溯源信息进行数字签名的有效性。

2.2 方案描述

本文方案实现在区块链溯源系统中溯源信息的安全上链，保证溯源信息的真实性、透明性和不可抵赖性。通过Schnorr门限签名方案实现链下对签名所需信息的生成与交互。采用Pedersen可验证秘密共享方案实现无可信中心分配组私钥。根据溯源系统中的溯源信息上传场景设置4种角色，分别是溯源信息上传者、门限签名成员、签名合成者和签名验证者。其中门限签名成员为溯源信息所涉及到的各个企业和供应商。区块链门限签名方案是一种通过节点间的相互协作来生成秘密份额的方案。在该方案中，节点之间共同参与验证信息的计算，确保验证结果的正确性。当验证结果正确时，会生成每个区块链节点的组公钥和个人私钥。这种基于门限签名的机制保证了系统的安全性和可信度。通过节点之间的协作，每个节点都承担一部分计算和验证的责任，使得整个过程更加安全可靠。其方案逻辑如图1所示。

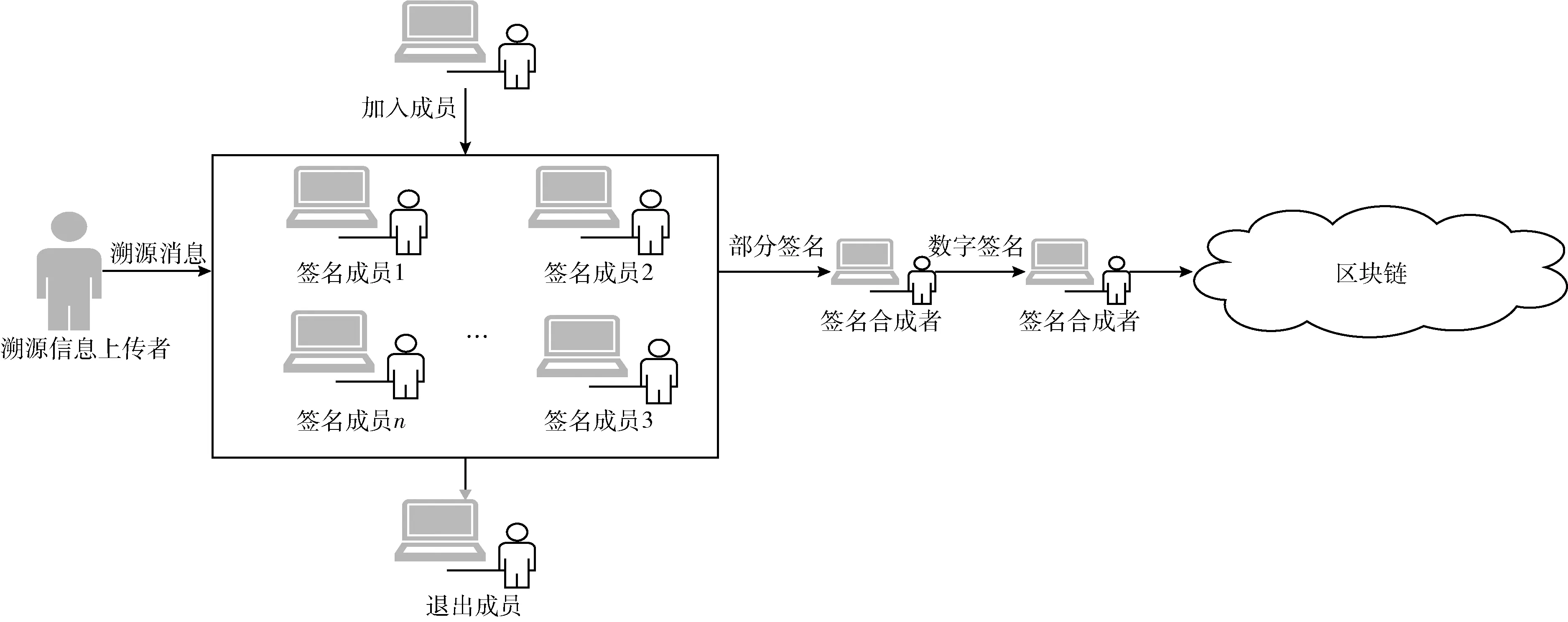
图1 方案逻辑

如图1所示，溯源信息上传者上传溯源信息M。门限签名成员使用个人私钥生成部分签名。签名合成者验证每个部分签名，并合成部分签名形成最终的门限签名。签名验证者进行签名验证，并将溯源信息上链，上链过程在本文不作描述。其中由于门限签名成员为溯源信息的相关者，在实际生产环节中可能会发生变动，因此本文方案允许门限签名成员的动态加入和退出。

2.3 动态Schnorr门限签名设计

本文方案共包括5个算法，分别为密钥生成算法TGenkey、门限签名算法TSign、签名验证算法Verify、签名成员加入算法UserAdd和签名成员退出算法UserDelete。

2.3.1 密钥生成：TGenkey

(1)区块链溯源系统参数初始化

(2)签名成员之间相互协作产生秘密份额

假设在区块链系统中溯源信息有n个相关成员Pi，i=1，2，…，n，t为阈值，每个成员节点都有其唯一的标识符IDi。Pi表示执行操作的一方，Pj表示与Pi进行交互的另一方。此环节产生用户Pi的公私钥对 (uski，upki)， 以及子密钥di和组公钥mpk。具体过程如下：

1)每个门限签名成员节点Pi，i=1，2，…，n选择随机数x∈[1，q-1] 作为他的用户私钥uski， 则对应的用户公钥upki=yi=xiG。Pi广播其公钥upki。

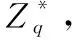
fi(x)=xi+ai，1x+ai，2x2+…+ai，t-1xt-1modq

(5)

节点Pi计算Ci，k并向其它节点广播

Ci，k=ai，kGmodq，k=1，…，t-1

(6)

同时Pi为其它n-1个成员计算共享子密钥si，j， 并通过点对点通道发送给Pj，j=1，2，…，n，j≠i

si，j=fi(IDj)

(7)

3)区块链节点Pj接收到Pi发送的si，j后，通过Pi广播的Ci，k对其进行验证，核实共享子密钥是否有效。如果下述等式成立则接收消息，否则将终止密钥生成算法

(8)

4)节点Pj验证所有其它节点发送给它的共享子密钥后，通过下述公式生成其子密钥dj，并广播其子公钥djG

(9)

5)在所有成员计算完dj后，组私钥为

(10)

任意t个门限签名成员可以根据拉格朗日差值公式恢复组私钥d，并且由此计算出组公钥mpk

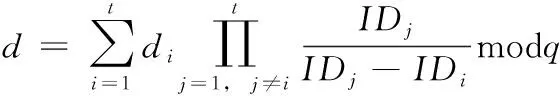
(11)

2.3.2 门限签名：TSign

每次门限签名由集合P={P1，P2，…，Pn} 中的t个成员Pi，i=1，2，…，t完成签名。签名成员通过其子密钥di对溯源信息M进行部分签名，将生成的部分签名发送给指定的签名合成者，由该合成者对每个部分签名进行验证，并合成最终的签名 (M，r，s)。门限签名具体过程如下：

(1)Pi，i=1，2，…，t生成随机数ki∈[1，q-1]， 计算Wi=kiG，Qi=diG是Pi的子公钥。Pi广播Wi。

(2)当Pj接收到其它t-1个成员的Wi，i=1，2，…t，i≠j后，由此计算W和它的横坐标x

(12)

(3)Pj计算e=xmodq， 再通过要签名的溯源信息M计算r=H(e‖M)。 接下来Pj计算sj， 并将部分签名 (M，r，sj) 通过安全点对点通信通道发送给签名合成者

sj=kj+djrmodq

(13)

(4)签名合成者在接收到Pj发送的部分签名后对其进行验证下述等式是否成立，若不成立则终止门限签名算法

Wj=sj-H(e‖M)·Qj

(14)

2.3.3 签名验证：Verify

签名验证者在接收到 (M，r，s) 后对门限签名进行验证。具体过程如下：

(1)签名验证者通过组公钥Q对签名进行验证，依次计算 (x′，y′)，e′和r′

(x′，y′)=sG-rQe′=x′modqr′=H(e′‖M)

(15)

(2)若r′=r， 则签名正确，若等式不成立则签名失败。

2.3.4 签名成员加入：UserAdd

当溯源信息涉及的签名成员集合P需要新成员Pr加入时，Pr需要满足以下几点条件。①已存在的成员节点的子密钥di(i=1，2，…，n) 不会发生改变。②新加入的节点不会改变组公钥Q。③新节点可以生成自己的子密钥dr且不暴露其它成员的子密钥。假设Pr的身份标识为IDr， 具体过程如下：

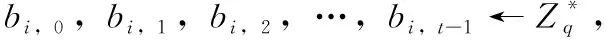
gi(x)=bi，0+bi，1x+bi，2x2+…+bi，t-1xt-1modq

(16)

Pi计算相应的C′i，k并广播它

C′i，k=bi，kGmodq，k=0，1，…，t-1

(17)

同时，Pi为其它n-1个成员计算共享子密钥s′i，j， 并通过安全通道将其发送给Pj

s′i，j=gi(IDj)

(18)

(2)Pj收到Pi发送的s′i，j后，核实其是否有效。如果等式(19)成立，则接收该消息

(19)

(3)Pj在核实s′i，j后通过下述公式计算临时子密钥d′j， 并通过安全通信通道将d′j发送给新加入的节点Pr

(20)

(4)新节点Pr在接收到至少t个成员Pi，i=1，2，…，t发送的d′j后，计算自己的子密钥dr

(21)

2.3.5 签名成员退出：UserDelete

当溯源信息所涉及的签名成员集合P有成员退出时，Pi(i=1，2，…，n-1) 需要重新构建每个成员的子密钥di(i=1，2，…，n-1)， 同时确保组私钥和组公钥保持不变。假设退出的成员为Pw，其身份标识为IDw，成员退出具体过程如下：

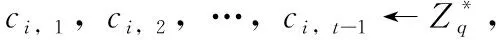
hi(x)=ci，1x+ci，2x2+…+ci，t-1xt-1modq

(22)

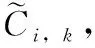
(23)

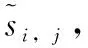
(24)

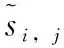
(25)

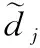
(26)

最后，Pj重构并更新其它成员的共享子密钥，即删除节点Pw的共享子密钥，实现节点Pw的退出。

3 方案分析与实验

3.1 正确性分析

本文所提出的动态Schnorr门限签名方案的正确性分析包括门限签名、动态添加成员和动态删除成员。分别为签名验证者可以验证有效的Schnorr门限签名；新加入的门限签名成员可以计算有效的子密钥，并计算组公钥；当门限签名成员退出时，组私钥和组公钥不会发生变化。

(1)门限签名正确性分析

签名验证者在接收到关于溯源消息M的门限 (M，r，s) 后，通过等式(15)验证签名的有效性。等式(15)成立的证明过程如下：

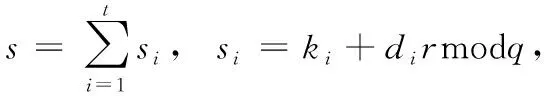
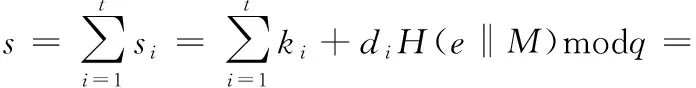
由于上述证明，所以签名验证者计算e′=x′modq，r′=H(e′‖M) 后，若签名正确则e′=e，r′=r， 证明了签名的有效性。

(2)成员动态添加的正确性

节点Pi，i=1，2，…，n发送给新加入成员Pr的d′j符合拉格朗日插值多项式模型，那么新加入的节点Pr在收到其它t个成员的临时秘密份额d′j后，可以通过式(21)计算出其秘密份额dr。

证明

因为

ηi(IDj)=fi(IDj)+gi(IDj)=(xi+bi，0)+(ai，1+bi，1)x+…+(ai，t-1+bi，t-1)xt-1modq

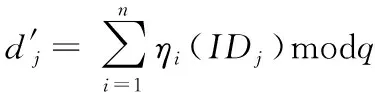
又因为根据式(20)得gi(IDr)=0， 所以

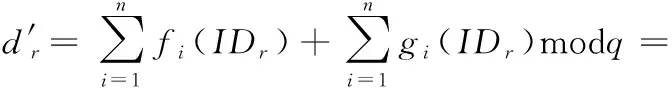
(27)

根据式(10)和式(27)，可以得出新加入的节点Pr的临时子密钥d′r和dr相等，所以Pr在未暴露其它成员的子密钥的同时有效地生成了其子密钥dr， 并可以通过式(11)计算组公钥。

(3)成员动态退出的正确性

集合P中有成员退出后组私钥d不发生改变。

因为hi(0)=0， 所以根据式(26)可得

(28)

由式(28)可知，成员退出后组私钥未发生改变，所以通过式(11)计算的组公钥也不会发生改变。

3.2 安全性分析

3.2.1 去中心化

实现门限Schnorr门限签名的常用方法是将组私钥分为n份，并由可信第三方分发给每个成员。通过将子密钥交由可信第三方完成数字签名，t个成员即可实现门限签名。然而，该方法存在一个潜在的问题，即一旦可信第三方出现故障，就无法进行数字签名的操作。本文所提方案在区块链溯源系统中，签名集合P中的成员通过安全通信通道进行通信，交互式生成子密钥和部分门限签名。在本文方案中，为了确保签名的有效性，采用了由签名合成者进行部分验证和签名合成的步骤。这个过程可以保证签名的正确性和一致性。最终，由签名验证者对签名进行验证，并将验证通过的签名广播到区块链溯源系统中。具体而言，本文方案实现了完全去中心化的目标，主要包括以下几个步骤：

在密钥生成算法中，门限签名成员节点Pi通过式(6)计算Ci，k并向其它节点广播，同时Pi为其它n-1个成员通过式(7)计算共享子密钥si，j， 并通过点对点通道发送给Pj，j=1，2，…，n，j≠i。Pj以此无需可信中心便可通过si，j计算其子密钥dj。

在签名算法中，集合P中的t个成员将其对溯源消息M生成的部分签名 (M，r，sj) 发送给签名合成者进行签名合成和部分签名验证。

同理，在签名成员加入和退出时集合P中的节点通过式(17)、式(18)、式(23)和式(24)计算需给其他成员发送的信息。经过点对点通道和广播的形式无需可信第三方完成签名成员加入和退出时子密钥的新增和更新操作。

3.2.2 不可伪造性分析

不可伪造性是动态Schnorr门限签名重要的安全要求之一。不可伪造攻击模型及具体分析如下。

(1)假设敌手A是第三方攻击者，伪装成合法签名者。其目的是通过伪造门限签名算法Tsign过程中所需要的子密钥dA的值来与其他参与者共同生成有效的签名。

敌手A在获取到系统公共参数 (Fq，E，G，q，a，b，H) 后，被敌手A腐败的成员S计算敌手A的公私钥对 (uskA，upkB) 和其子密钥dA。 在签名阶段，S将签名 (M，r，s) 发送给敌手A，敌手A对溯源消息M构造一个有效签名。在敌手A伪造签名阶段，为了保证伪造签名的有效性，随机数k必须被伪造。随机数k是由集合P中的t个成员随机生成的随机数ki相加而得，无法被公开获取。而且ki在签名过程过没有被重新生成过，因此A只能从kiG中尝试获取随机数。此问题是椭圆曲线离散对数问题，该问题是椭圆曲线密码安全理论的基础，属于非确定性多项式完备问题，因此敌手A无法成功地伪造签名。

(2)假设敌手A是签名成员集合P中的一个不诚实的成员，并且破坏了其它一些成员节点以生成有效的共享私钥来伪造签名。它的目的是破坏门限签名算法Tsign过程中所需要的子密钥，从而与其它参与者生成一个有效的签名。

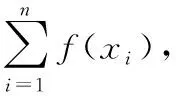
3.2.3 抗合谋攻击

Schnorr门限签名方案的不可伪造性决定本文方案至少t个成员才能生成数字签名，而少于t个则不能。

假设签名集合P中有t-1个恶意签名者进行合谋攻击，伪造门限签名。

在签名阶段每个成员Pi(i∈[1，t-1]) 生成随机数ki∈[1，q-1]， 并伪造第t个成员的随机数kt和子密钥dt。 恶意签名者Pi通过式(12)和式(13)计算对溯源信息M的部分签名信息。在签名验证阶段，由于其伪造的子密钥dt在验证阶段无法通过式(15)的验证，致使签名失败。恶意签名者无法通过重新构造多项式f(xi) 以获得子密钥dt， 因离散对数难题也无法通过组公钥获取到组私钥d。所以子密钥dt被正确伪造的概率与直接伪造组私钥d成功的概率相等，这意味着，攻击者无法通过伪造子密钥来突破门限签名的安全性。又因为数字签名具有不可伪造性，t-1个成员无法联合生成任何交易的签名。因此本文方案可以有效地抵御成员间的合谋攻击。

3.3 性能分析

3.3.1 方案对比分析

本节从签名方式、去中心化、是否能验证份额以及是否允许节点动态加入和退出4个方面与其它方案进行方案对比。

如表1所示，本文所提方案满足去中心化、对溯源信息的不可抵赖性和对签名的不可伪造性，且允许签名成员的动态加入和退出。本文方案在区块链溯源应用中更具有优势。

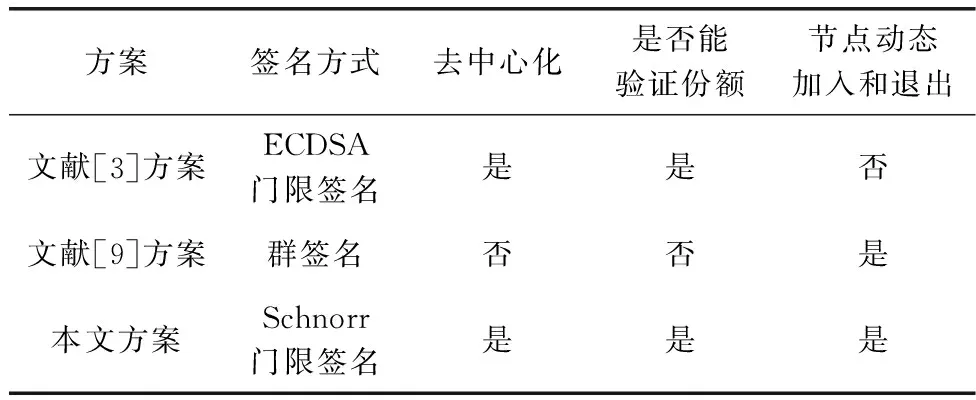
表1 方案对比

3.3.2 效率分析

表2展示了本文提出的Schnorr门限签名方案与其它签名方案在门限签名阶段和签名验证阶段的计算成本对比结果。其中Td表示签名算法在椭圆曲线上进行标量乘法运算或模幂运算的计算成本，Tm表示模乘运算的计算成本，Th表示哈希函数SHA256运算的计算成本，Tc表示模求逆运算的计算成本，t为阈值。模加法、模减法运算的计算量与模幂运算、模乘运算以及标量乘法运算相比可忽略不计，因此本文不统计模加法和模减法运算的计算成本。

表2 门限签名计算成本对比

如表2所示，在签名阶段和签名验证阶段，本文方案的计算成本小于文献[3]和文献[12]中所提方案。由于文献[10]中所提方案的计算成本较为接近。但是，由于文献[10]所提方案在签名阶段和在签名验证阶段进行的模幂运算更为复杂，因此本文所提方案的计算成本实际小于文献[10]所提方案。且文献[3]所提方案缺少签名节点动态加入和退出机制。文献[12]所提方案缺少节点动态退出机制。

对于本文方案的门限签名算法和签名验证算法的计算成本进行仿真对比实验。门限签名阶段主要由阈值t决定计算开销。实验环境为64位ubuntu-20.04.2.0系统，CPU为lntel Core i7-6500U @2.50 GHz，采用GO语言进行代码编写。实验结果如图2和图3所示。

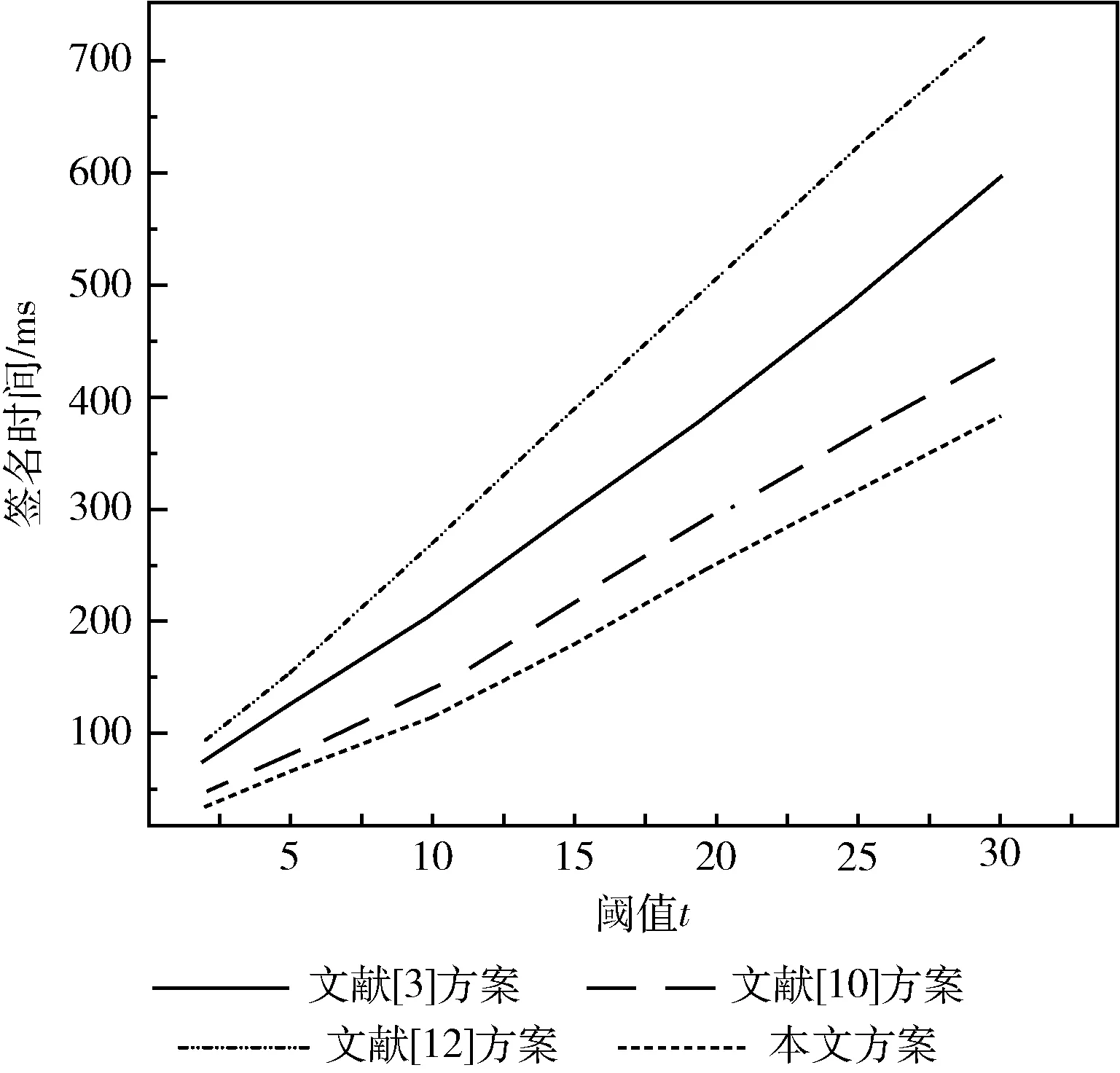
图2 签名时间对比

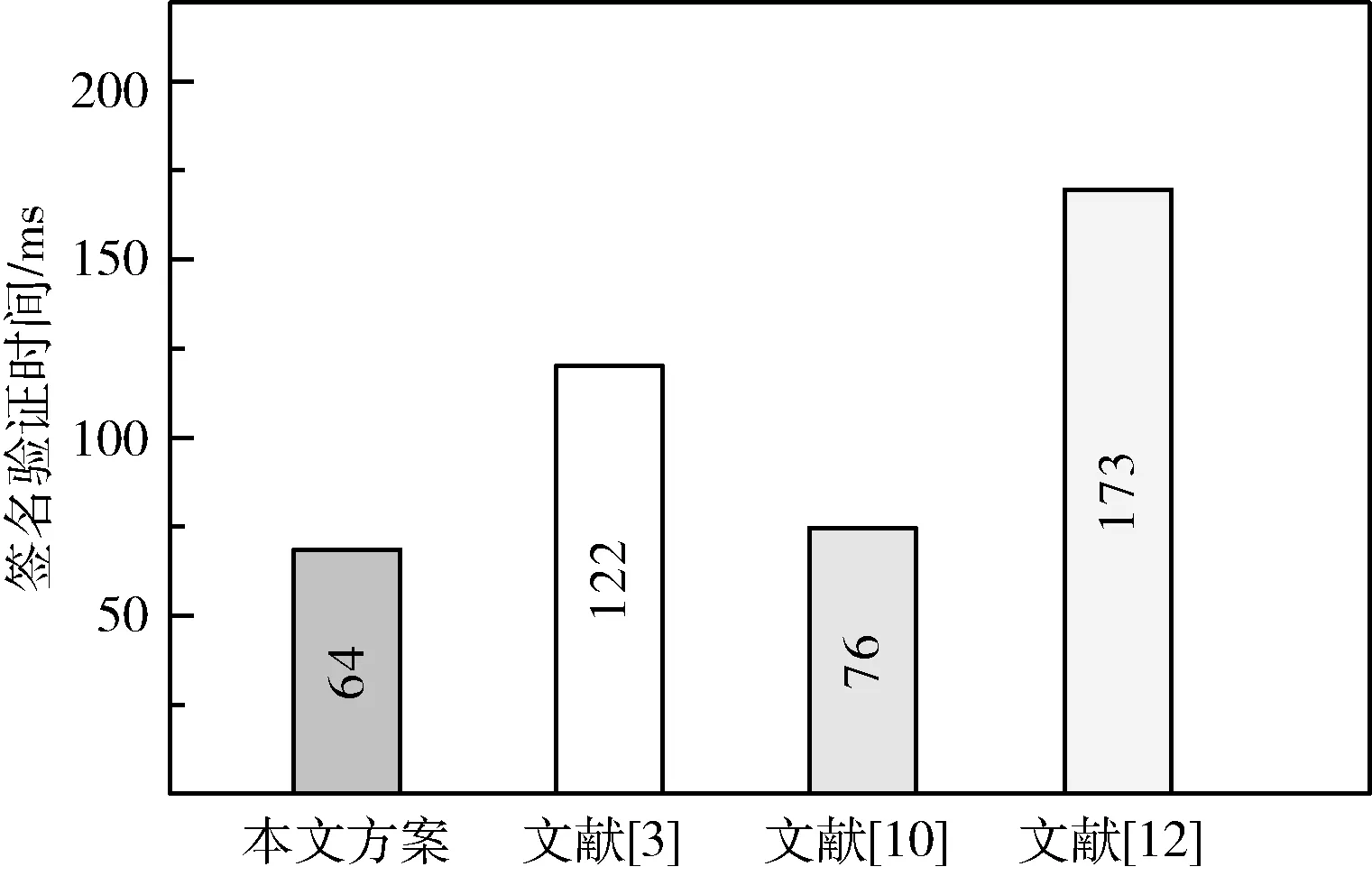
图3 签名验证时间对比

在实验环境和阈值相同的情况下，分别测试100次不同方案的签名时间，实验结果取平均值。由图2可知，相对于文献[3]、文献[10]和文献[12]所提门限签名方案，本文方案的签名时间较短，在阈值为20时，签名时间约为247 ms，具有较高的签名效率。

在实验环境相同的条件下，分别对本文方案、文献[3]所提方案、文献[10]所提方案和文献[12]所提方案中的签名验证阶段进行100次测试，实验结果如图3所示。测试结果表明，相对于文献[3]、文献[10]和文献[12]所提方案，本文方案在签名验证阶段具有较高的签名验证效率。并且本文方案有签名节点动态加入和退出机制，更适用于区块链溯源场景。

4 结束语

根据区块链溯源场景需求，本文提出了一种Schnorr门限签名方案。解决了溯源信息相关者对溯源信息进行签名的不可抵赖性、抗合谋攻击和签名效率问题。签名成员协作生成子密钥和签名，实现了区块链溯源系统在签名环节的完全去中心化。在抗合谋攻击中只有大于t个成员进行合谋才能进行签名伪造。方案允许签名成员动态加入和退出，具有良好的可调整性，且在成员加入和退出时，组私钥和组公钥不会发生改变。

本文提出的Schnorr门限签名方案基于Pedersen可验证秘密共享，在门限签名阶段和签名验证阶段的计算效率较高，其安全性使其适用于涉及签名成员动态加入和退出的溯源系统。