橡胶砂液化特性的动扭剪试验研究
王珂琦, 朱小军, b*
(扬州大学 a. 建筑科学与工程学院; b. 岩土工程研究所, 江苏 扬州 225127)
橡胶砂是一种经济型填料, 其力学特性研究在建筑工程应用中具有重要意义.姚玉文等[1]采用弯曲-伸缩元法对橡胶砂进行研究, 发现在相同围压下, 橡胶砂初始剪切模量和侧限模量随橡胶颗粒掺量的增加而逐渐减小; 周恩金[2]和Ghazavi[3]等采用动扭剪试验系统研究发现, 试样抗液化能力随着橡胶颗粒掺量和粒径的增加而增强; 刘方成等[4-5]研究发现, 当橡胶颗粒含量较少时, 橡胶颗粒分布在砂颗粒空隙中参与整体受力, 橡胶砂动剪切模量较低,当橡胶含量增加时, 橡胶颗粒被砂颗粒包围但不嵌入其中, 形成拱效应, 动剪切模量较大; 研究人员还发现, 橡胶砂的阻尼比趋于稳定时所需的循环次数随竖向应力减小而减少, 且橡胶砂的阻尼比随橡胶颗粒掺量及含水率的增加而减小[6-8]; 刘启菲[9]和祝梦凡[10]等认为橡胶颗粒含量增加时, 橡胶砂的内摩擦角相应减小, 而相对密实度的增加可以提高其抗剪切能力; Amuthan等[11]通过研究砂-橡胶混合料和砂的界面行为, 发现其界面系数在0.85~1范围内变化; Wu等[12]认为橡胶颗粒可显著改善宿主砂性土的动力性能, 在隔震减震技术中有巨大应用潜力; Okur等[13]对橡胶砂开展共振柱和动扭剪试验, 发现橡胶质量掺量为 5%时, 橡胶砂的剪切模量和阻尼比更接近于纯砂.目前, 关于橡胶颗粒对饱和砂土影响的研究多数针对静力特性方面, 而对橡胶砂动力特性的影响尚无明确、系统的研究结论.故本文拟通过动扭剪试验研究橡胶掺量、循环应力比、相对密实度、频率、有效围压等对橡胶砂动力特性的影响, 为橡胶砂理论研究与实践应用提供相应的参考和借鉴.
1 试验概况
1.1 试验材料
本试验采用粒径为0.5~2 mm的粗砂, 颗粒密度为2.70×103kg·m-3, 平均粒径为0.714 mm, 不均匀系数为1.492, 曲率系数为0.921, 级配曲线见图1.筛取粉碎的废橡胶轮胎, 得到粒径为2~4 mm的干橡胶颗粒, 颗粒密度为1.28×103kg·m-3, 平均粒径为3.382 mm, 不均匀系数为1.402, 曲率系数为1.125.
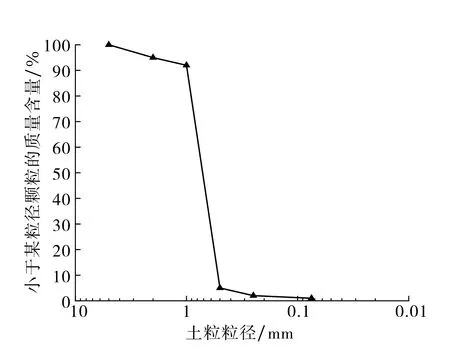
图1 砂土粒径级配曲线Fig.1 Particle size grading curve of sand
1.2 试验方案
采用湿击法制作内径60 mm、外径100 mm、高度200 mm的空心圆柱形橡胶砂试样.制样时先将内橡胶膜固定到基座上, 再将大尺寸的内膜具四瓣膜插入橡胶膜内, 与底座卡合, 用铁箍套于外围进行固定,避免歪斜、褶皱等.然后将小尺寸的一对内模具插入四瓣膜内固定, 形成圆柱环内腔.在底座透水石上放置滤纸, 再将三瓣膜的外膜具包裹外橡胶膜安装在底座上, 形成圆柱环结构.最后将橡胶砂混合土装入圆柱环内.由于空心扭转试验的试样尺寸较大, 故采取二氧化碳饱和、水头饱和、反压饱和等3种措施保证试样达到饱和度要求.通过压力加载测试孔隙水压力系数,若数值稳定并大于0.95, 则饱和度达到要求.试样饱和后, 设置相同的内外围压进行等向固结, 固结时间为8 h.观察反压体积曲线是否处于水平趋势, 并读取每小时的体积变化, 若体积变化小于60 mm3·h-1, 则固结完成, 然后在动扭剪试验系统软件中选择加载模式,并设定相关参数进行试验.
2 试验结果分析
2.1 橡胶掺量的影响
在频率f为0.1 Hz, 有效围压为100 kPa, 循环应力比CSR为0.15, 试样相对密实度Dr为0.3的条件下, 改变橡胶颗粒质量分数Rf, 测试橡胶颗粒掺量对橡胶砂孔压和剪切应力应变的影响, 结果如图2所示.
由图2(a)可知,Rf=5%~30%时, 橡胶砂的孔压发展模式均呈现先快速增长后趋于平稳的趋势.在孔压快速增长阶段,Rf为5%时的孔压发展曲线斜率较缓, 但在孔压发展后期出现二次快速增长现象, 平稳阶段的累积孔压随Rf的增加而呈现下降趋势.Rf=20%的橡胶砂在振动40周后, 循环孔压趋于稳定, 最大孔压比约0.95, 达到临界液化水平, 相比于Rf=10%的橡胶砂发生液化时的周数增加了148%;Rf=30%的橡胶砂的孔压在振动至60周后逐渐平稳, 最大累积孔压比为0.91, 未达到孔压破坏标准.说明橡胶掺量的增加可提高橡胶砂的抗液化水平.这是由于试样中橡胶掺量较大时, 橡胶颗粒起到骨架作用, 砂粒填充在橡胶颗粒之间的孔隙中, 使骨架结构更为密实, 不易液化.此外, 由于掺入橡胶颗粒的粒径较大, 橡胶砂渗透系数增加,在循环载荷作用下试样的孔压更易消散.同时橡胶颗粒降低了橡胶砂的弹性模量, 在循环荷载作用下可产生回弹效应, 使橡胶颗粒与砂颗粒间接触更紧密, 当孔压急剧上升时, 能降低孔压的累积增长趋势.
图2(b)显示, 不同橡胶掺量下试样的剪切应力-应变曲线基本均以原点为中心对称发展, 这表明在循环扭剪载荷作用下, 橡胶颗粒的掺入没有引起材料明显的各向异性.当橡胶颗粒的质量分数提高时, 试样的剪切应变发展范围增大,滞回曲线的斜率随之减小, 说明其动弹性模量逐渐减小, 刚性减弱.结合图2(c)的广义剪切应变发展曲线可知,随着橡胶含量的增多, 广义剪切应变的累积程度逐渐减缓, 说明橡胶砂的抗变形能力相应增强.
2.2 循环应力比的影响
在频率为0.1 Hz, 有效围压为100 kPa,Dr为0.3,Rf分别为10%, 20%, 30%的条件下, 试样孔压比在不同循环应力比下的发展曲线如图3所示.由图3可知, 橡胶掺量相同时, 循环应力比越大, 循环孔压比趋于平衡时所需的振动周次越少, 这是因为CSR增大时, 试样中橡胶颗粒压缩、回弹的程度相应提高, 导致循环孔压比增速加快, 试样更快发生液化.
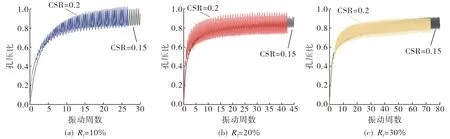
图3 孔压比随循环应力比发展的曲线Fig.3 Pore pressure ratio development curve with cycle stress ratio
2.3 相对密实度的影响
在频率为0.1 Hz, 有效围压为100 kPa,Rf为30%, 循环应力比分别为0.15和0.20的条件下, 相对密实度对试样孔压的影响如图4所示. 由图4可知,Dr为0.3和0.6时, 试样的孔压比均呈现先快速增长后趋于平稳的发展规律, 且两种密实度的孔压曲线均有重合.当Dr=0.3时, 橡胶砂的孔压增长较快, 达到临界液化水平; 当Dr=0.6时, 其循环孔压幅值相对较小, 未达到液化水平.增大循环应力比CSR时, 此现象更为明显.当Rf=30%, CSR=0.2时, 相对密实度对剪切应变时程曲线的影响见图5.由图5可知,Dr较小时橡胶砂剪切应变幅值更大, 发展速度更快, 这是因为Dr较小的橡胶砂结构更为疏松, 颗粒在液化时发生移动破坏; 而Dr较大的橡胶砂颗粒在液化时的运动范围有限, 颗粒排列方式更稳定.且橡胶颗粒掺量较大时, 液化现象也难以发生.综上, 随着相对密实度增大, 橡胶砂发生液化的难度增加.
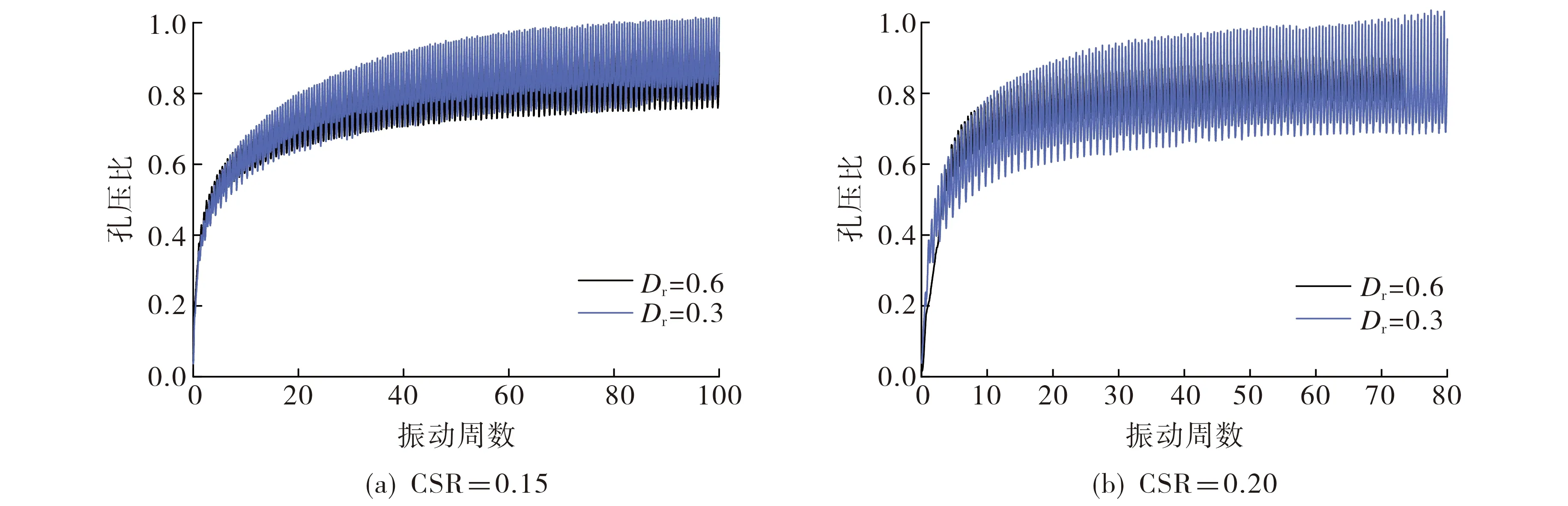
图4 不同密实度下孔压比发展曲线Fig.4 Pore pressure ratio development curve with different density
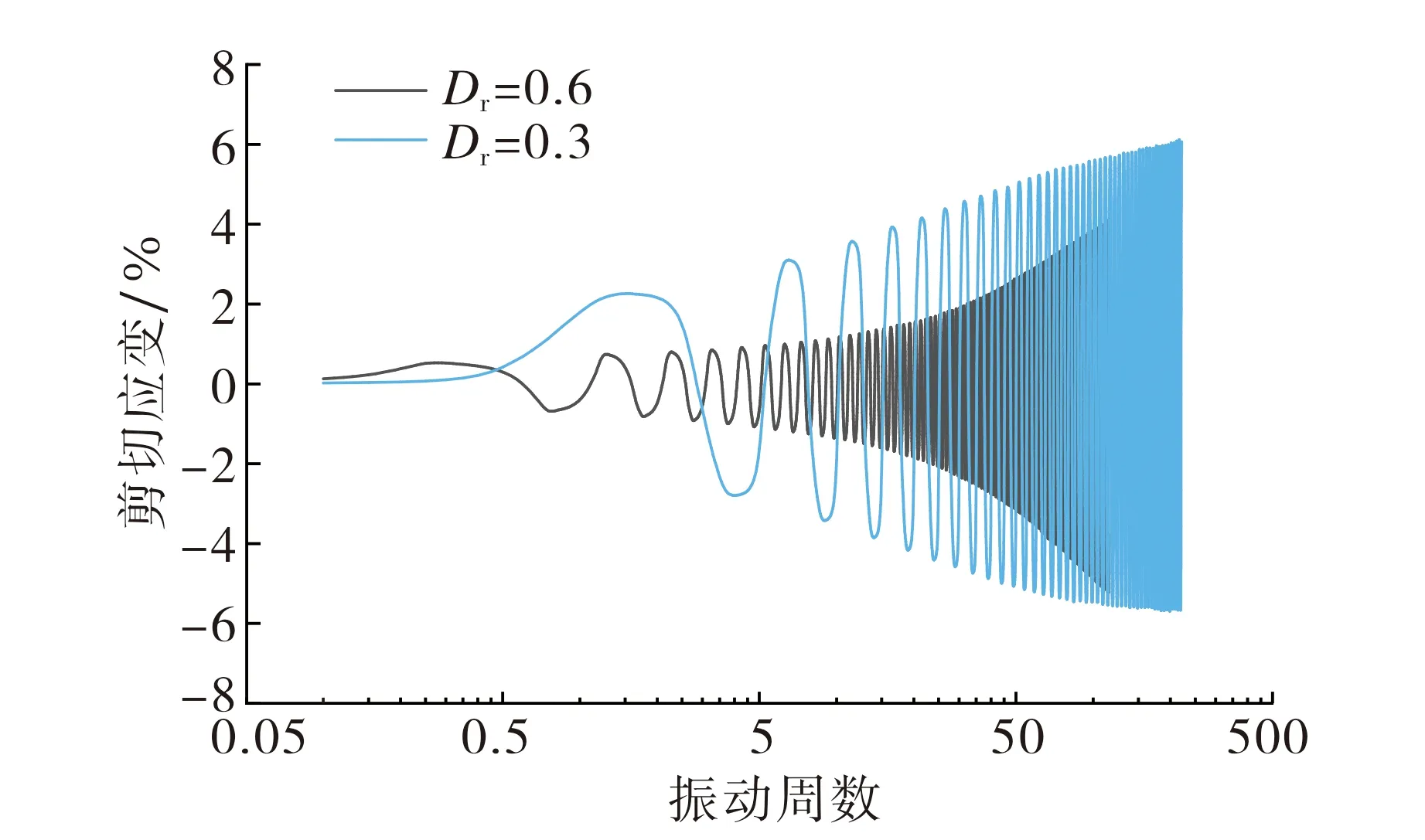
图5 不同密实度下剪切应变时程曲线Fig.5 Shear strain time history curve with different density
2.4 频率的影响
在有效围压为100 kPa, 循环应力比为0.15,Dr为0.3的条件下, 橡胶砂振动频率对孔压发展曲线和剪切应变时程曲线的影响见图6和图7.由图6可知, 频率由0.1 Hz提高到0.5 Hz后, 孔压发展速度明显加快.图7显示, 频率较低的试样剪切应变幅值较低且发展速度较慢, 这是由于在频率较低时, 扭矩的周期变慢, 橡胶砂中的橡胶颗粒来不及充分回弹, 这也是循环孔压发展滞后的原因.因此, 在时间一定的情况下, 试样的液化速度随着频率的增大而加快.
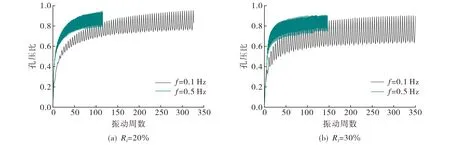
图6 不同振动频率下孔压比发展曲线Fig.6 Pore pressure ratio development curve with different vibrational frequency
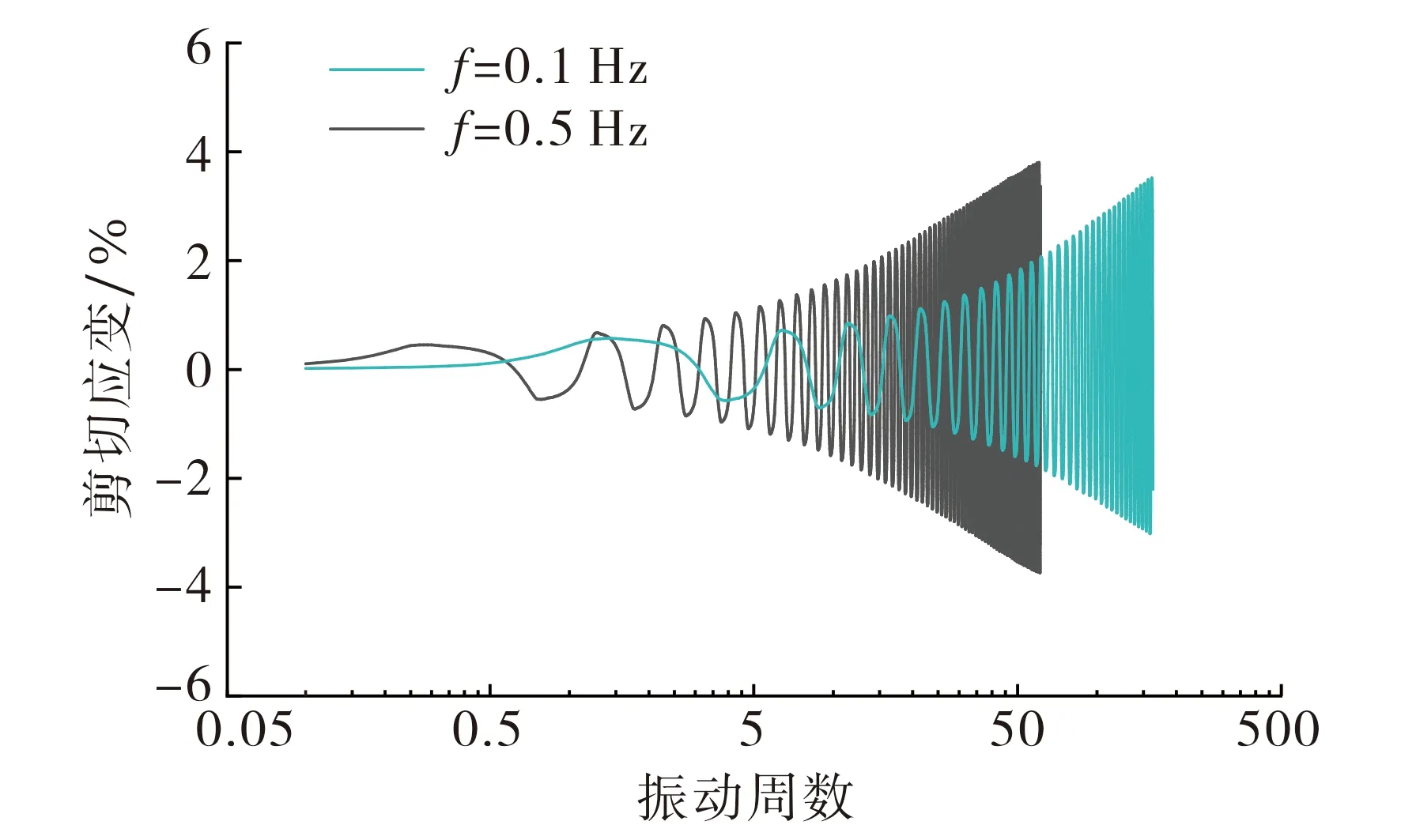
图7 不同频率下剪切应变时程曲线Fig.7 Shear strain time history curve with different vibrational frequency
2.5 有效围压的影响
在频率为0.1 Hz, 循环应力比为0.20,Rf为30%的条件下, 有效围压对孔压的影响关系曲线见图8.由图8可知, 有效围压100 kPa下, 橡胶砂在振动约100周后达到液化水平, 当有效围压为200 kPa时, 橡胶砂的循环孔压最高仅能达到有效围压的92%, 经过多次振动后也不能达到临界液化水平, 孔压保持稳定后不再增长, 但此时的循环孔压较大.由于各颗粒间的应力随着有效围压增加而增加, 橡胶与砂之间的连接更密实, 摩擦力相应增加, 橡胶颗粒进一步压缩并回弹, 使橡胶砂的抗液化能力提高.对比不同密实度下试样的孔压发展情况可知, 在密实度为0.3时, 不同围压下的试样在振动60周后达到液化水平; 而密实度为0.6时, 有效围压为100和200 kPa下, 试样分别振动100周和200周以上才能发生液化.
3 弹性模量和阻尼规律的分析
3.1 弹性模量的变化规律
在频率为0.1 Hz, 有效围压为100 kPa, 循环应力比为0.15,Dr为0.3的条件下, 橡胶砂剪切应变γ和弹性模量E关系的拟合曲线见图9.由图9可知, 4种不同Rf的橡胶砂的弹性模量均随应变的增大而减小, 这是因为试样在载荷下产生较大应变时, 内部结构变得松散.对比图中初始弹性模量可知,其随着橡胶颗粒质量分数的增大而降低.这是因为橡胶砂的形变主要来自橡胶颗粒的压缩和颗粒孔隙间的压缩, 而纯砂的压缩形变仅来自孔隙间的压缩,所以橡胶砂在循环载荷下的弹性形变大于纯砂, 且变形能力随着橡胶颗粒质量分数的增加而增强.因此在相同剪切应变下, 试样的动弹性模量随着橡胶颗粒质量分数的增加而减小.
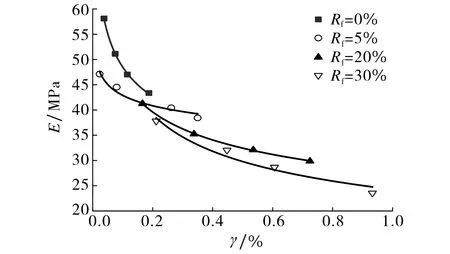
图9 橡胶砂弹性模量-剪切应变关系曲线Fig.9 Relationship curve of rubber sand mixture between elastic modulus and shear strain
3.2 阻尼比的变化规律
在频率为0.1 Hz, 有效围压为100 kPa, CSR为0.15,Dr为0.3的条件下, 橡胶砂剪切应变γ和阻尼比λ关系的拟合曲线见图10.由图10可知, 4种不同橡胶颗粒掺量的橡胶砂的阻尼比均随应变的增大而增大.这是因为试样结构随着应变增加而疏松, 孔隙增多, 所以阻尼比增大.纯砂的最小阻尼比λmin为 0.067, 当Rf为5%和30%时, 橡胶砂的λmin分别为0.153和0.225, 比纯砂分别提高了128.4%和235.8%.表明橡胶砂的阻尼比随着橡胶颗粒质量比的增加而显著增加.这是由于低弹性模量和高回弹性的橡胶颗粒在缓冲循环载荷的同时吸收了能量, 因此在循环载荷作用下橡胶砂的剪切应变滞后, 从而提高了阻尼比.
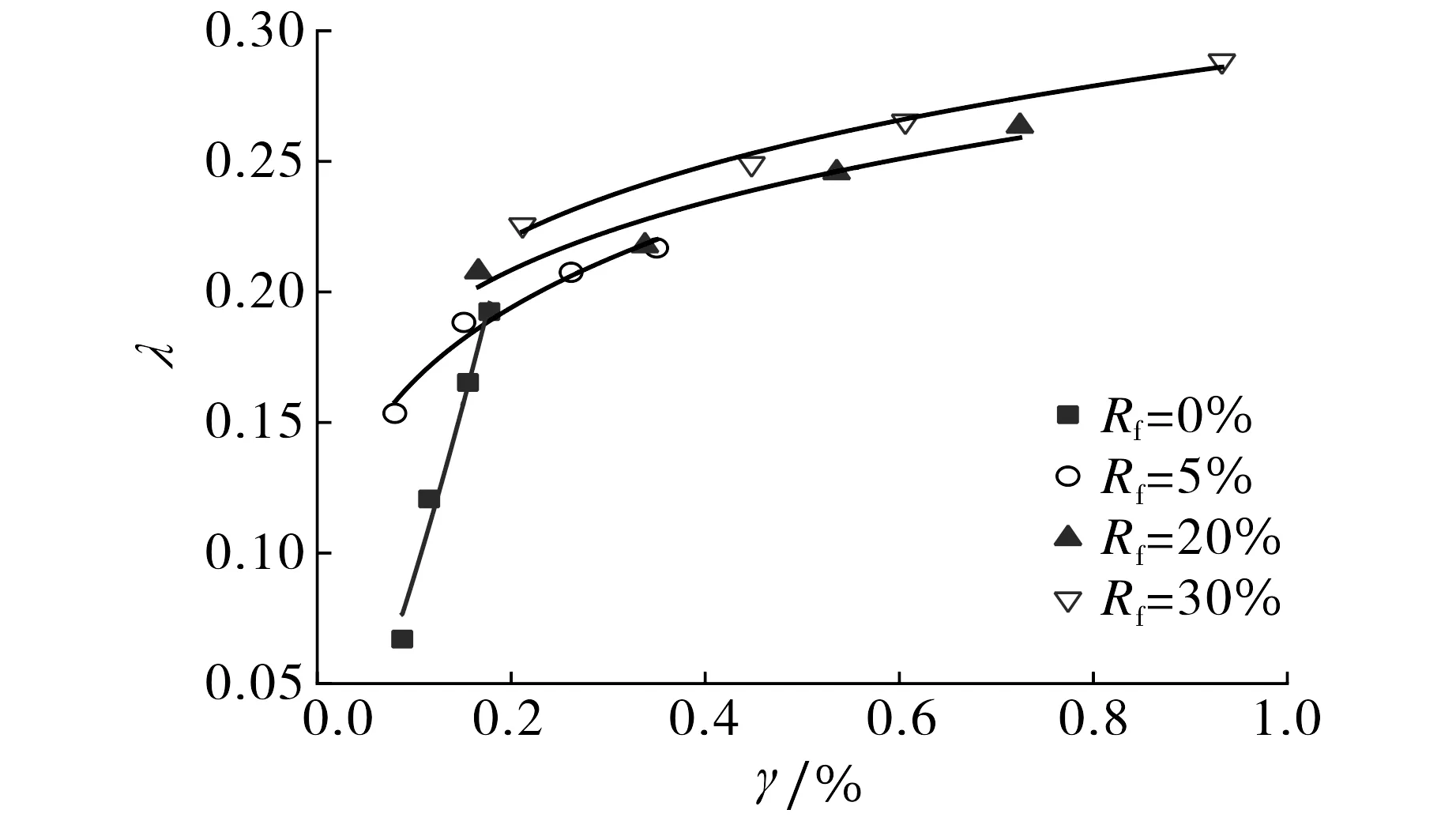
图10 橡胶砂阻尼比-剪切应变关系曲线Fig.10 Relationship curve of rubber sand mixture between damping ratio and shear strain
4 结论
在砂土中掺入橡胶颗粒可以提高砂土的抗液化性能, 改善其动力特性, 橡胶颗粒掺量越高, 橡胶砂孔压发展速度越缓慢, 越不容易液化; 有效围压、试样相对密实度及橡胶颗粒掺量的增加,可显著提高试样的阻尼比,试样更不容易破坏.当橡胶颗粒质量掺量低于30%时, 橡胶砂混合土的动弹性模量可以满足一般挡土墙或路基等填料的要求, 且阻尼比较大,具有良好的减震耗能效果.

