有理特征值问题两类改进的数值求解算法
陈小平, 魏 伟, 潘小明, 史雪莹, 罗 安
(1. 泰州学院数理学院, 江苏 泰州 225300; 2. 东南大学数学学院, 南京 210009;3. 南京林业大学理学院, 南京 210037)
考虑有理特征值问题: 寻找特征值λ∈R, 非零向量x∈Rn, 使得
T(λ)x=0,
(1)
其中T(λ)是关于参数λ的有理矩阵函数且T(λ)∈Rn×n, 并称(λ,x)为式(1)的一个特征对.上述问题广泛应用于高速列车自动发射器的优化[1]、流-固结构振动[2]和量子点结构计算[3-4]等.然而, 实际应用过程中往往无须求出有理特征值问题(1)的所有特征对, 研究者真正感兴趣的主要是部分特征对(λ,x)∈I×H, 式中I⊂R为某一区间,H⊂Rn是Hilbert空间.目前, 求解有理特征值问题(1)的第一类常见方法是通过线性化等方法[5-6]将原有理特征值问题(1)转化为等价的多项式特征值问题, 然后进行求解.第二类常用方法是直接将有理特征问题(1)视为一般的非线性特征值问题, 这类方法主要包括矩阵分解方法[7-10]、 插值类方法[11]、 投影类方法[12-14]和逐次近似方法[15-16]等.这些方法虽能较好地求解有理特征值问题(1), 但在求解时不能利用原有理特征值问题(1)的某些特殊结构或性质.最近, Chen等[17]研究了具有特殊结构的有理特征值问题(1)的谱性质, 并结合这些谱性质发展了求解有理特征值问题的二分迭代算法和Rayleigh函数迭代算法.然而, 该算法在实际计算时依赖初值的选取, 不合适的初值可能会导致迭代不收敛, 故本文拟通过区间变换来改进有理特征值问题的数值求解方法.
众所周知,有理特征值问题(1)中的有理矩阵函数T(λ)通常可表示成如下标准形式:
(2)
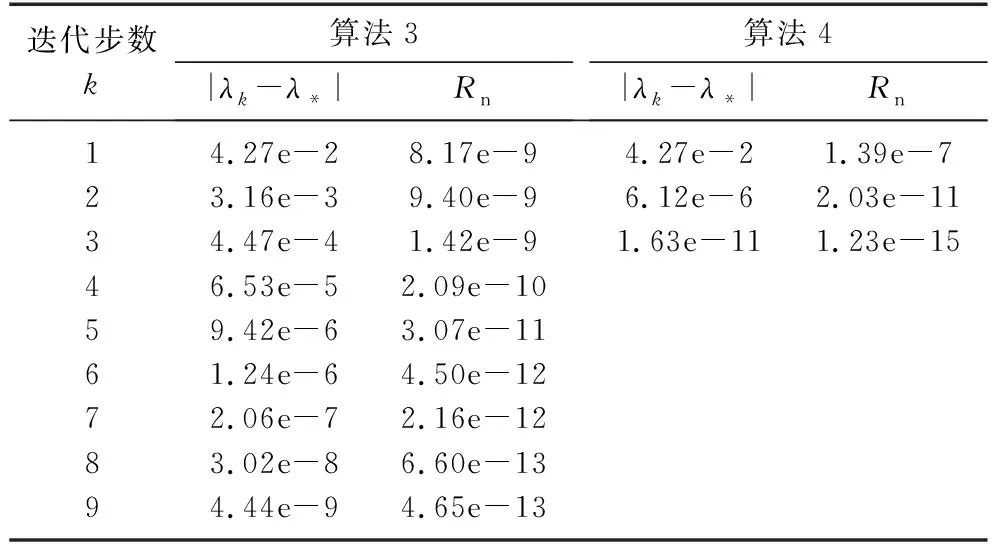
其中P(λ)=λmAm+λm-1Am-1+…+λA1+A0为矩阵多项式;fi(λ),gi(λ)分别是关于参数λ的阶数为mi,ni互质的标量多项式函数, 且mi (3) 其中fi(λ)=ai,mi-1λmi-1+…+ai,1λ+ai,0,gi(λ)=λni+bi,ni-1λni-1+…+bi,1λ+bi,0. 类似文献[17], 本文仅探讨有理特征值问题(3)在正半实轴上的特征值分布情况, 并假设如下[17]: 假设1矩阵Ai为对称正定矩阵, 对于任意i=1,2,…,m, 且A0为对称矩阵. 假设2矩阵Bi为低秩对称半正定矩阵, 对于任意i=1,2,…,j. 有理特征值问题(3)的谱理论详见文献[17].根据假设2和低秩扰动理论[18], 有理特征值问题(3)可近似转化为多项式特征值问题 (4) 一般事先无法预知有理特征值问题(3)的λ, 故若选定的σ接近于区间Il的边界, 则会导致算法1和算法2的计算效率较差,甚至算法失效, 即最接近σ的μ不在Il内.为改善上述问题, 本文基于区间变换法提出求解有理特征值问题的两种改进的数值方法. T1(ξ)x=0. (5) 不难发现,λ为问题(3)特征值的充分必要条件是:ξ为有理特征值问题(5)的特征值, 且上述问题具有相同的特征向量. 另外, 若计算有理特征值问题(3)在Il=(σl-1,σl)内的特征值λ.不妨令ζ=(λ-σl-1)/(σl-σl-1), 则λ=ζ(σl-σl-1)+σl-1, 式中ζ∈(0,1).将此式代入有理特征值问题(3), 则问题(3)变为新的有理特征值问题, 记作 T2(ζ)x=0, (6) 注1类似算法3, 可得求解有理特征值问题(3)的改进Rayleigh泛函加速迭代法(算法4), 即将算法3第8步中“ω=(ω+μ)/2”改为“ω=pl(x)”即可. 定理1若假设1~3均成立, 则算法3和算法4产生的迭代序列分别具有局部线性收敛性和二阶收敛性. 证明 由二分法以及Rayleigh商迭代收敛性[17]可知,算法3具有局部线性收敛性, 且算法4具有局部二阶收敛性. 通过与算法1和算法2的对比, 说明本文改进算法的有效性, 其中λk表示各算法运行第k步的近似特征值.类似文献[17], 数值分析时仅考虑有理特征值问题在I1=(0,η)和I2=(η,100)上特征值的分布, 并取参数η=1和精度τ=10-12. 例1[5]有理特征值问题 (7) 取n=1 000, 容易验证λ*=0.457 318 5为有理特征值问题(7)的精确特征值, 因为T(λ*)的最小奇异值小于10-9.利用MATLAB R2019a编程, 置σ=0.5, 运行算法3和算法4, 计算结果如表1所示.由表1可见, 算法3和算法4分别具有线性和二阶收敛性. 表1 算法3和算法4的数值结果 取n=2 000, 容易验证λ*=0.457 318 5和λ*=63.723 821 1分别是有理特征值问题(7)在区间I1=(0,1)和区间I2=(50,100)内的2个精确特征值, 因为它们的最小奇异值均小于10-9.分别置σ=0.5和σ=75, 不同算法的计算结果见表2.由表2可见, 算法3和算法4的数值效果分别优于算法1和算法2, 因此区间变换是有必要的.此外, 算法1和算法2能否计算出有效结果主要取决于σ取值是否合适.数值计算结果表明, 若σ取值接近各区间的边界,则计算会出现不收敛的情形. 表2 四种算法在区间I1和I2内的数值结果 取n=1 000,σ=1.ω取0.5和13时, 算法4的计算耗时分别为0.03和0.04 s, 而投影方法[19]在ω1=0.3,ω2=0.4,ω3=0.5,ω4=0.6和ω1=5,ω2=9,ω3=13,ω4=17条件下的计算耗时均达0.08 s.计算结果表明, 本文提出的算法4比文献[19]中的投影方法更快. 本文基于区间变换法提出两种求解有理特征值问题的改进的迭代算法以及相应的理论结果,新方法的收敛因子有待进一步研究.虽然数值实验验证了结论的正确性以及新算法的有效性, 但是对于更一般的有理特征值问题谱性质及其相应的数值求解算法有待深入研究.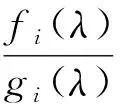
1 两种数值方法求解有理特征值问题
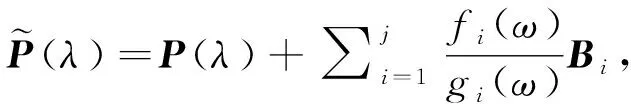

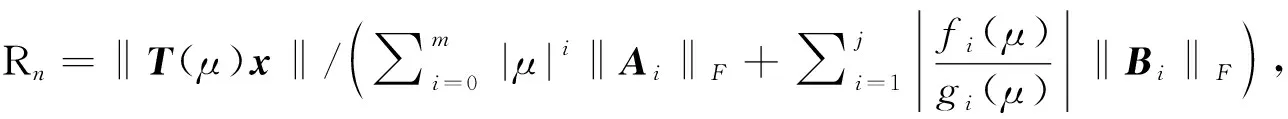
2 两种改进的数值方法求解有理特征值问题
2.1 两种改进的数值方法的构造
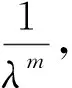


2.2 改进算法的收敛性
3 数值实验
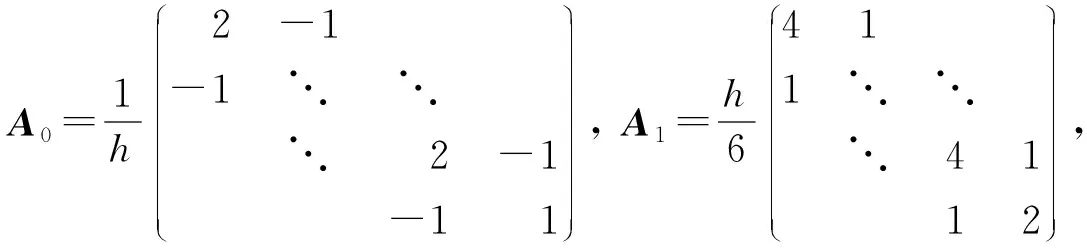

4 结论

