高转速低功耗非晶定子永磁无刷直流电机优化设计研究

孙海波，朱 锋，张志臻，庞雷宇，黄旭文

（1.佛山科学技术学院 材料科学与氢能学院，广东 佛山 528000；2.佛山中研磁电科技股份有限公司，广东 佛山 528241）

随着电机技术、驱动电子、微控制器和GPS 导航等科技的进步，无人机已广泛应用于航空摄影、电力巡检、物流服务、移动基站等重要的社会和经济领域［1-2］。续航性能是无人机的重要性能指标。影响无人机续航性能的因素有很多，主要包括：无人机自重、飞行速度、电池容量及电机效率等［3］。其中，采用更高速度运行的电机是提升电机效率及无人机续航性能行之有效的解决方案之一［4］。然而，高速条件下，传统硅钢材料由于其铁芯损耗（以下简称铁损）系数较高［5］，难以降低铁损提升效率。目前提升电机效率常用的方法有两种：一为采用低铁损磁性材料，如非晶纳米晶合金等；二为优化电机拓扑结构或电磁参数进行轻量化设计。

已有研究表明，非晶纳米晶合金软磁材料的应用在提高电机效率以及电机轻量化发展方向上有广阔前景［6］。Flyur R.Ismagilov 等［7］通过实验研究证明，将非晶材料应用于高速电机中，可使电机铁损降低5～7 倍。Jing Ou 等［8］基于非晶合金材料特性所设计的高速用永磁同步电机效率达94.91%。对于优化电机拓扑结构或电磁参数进行轻量化设计，国内外也进行了大量研究。彭珍等［9］使用二代非支配排序遗传算法（NSGA-II），建立了圆筒型永磁直线电机的多目标优化模型，对电机功率及效率进行优化后，电机功率提升了13.08%，电机效率提升了7.35%。Yong Kong 等［10］设计并基于负载周期优化了应用于无人机系统的外转子永磁同步电机，结果表明，采用非晶合金制造定子铁芯性能优越，通过优化设计，在配备相同电池容量的一次飞行中，无人机系统增加了10.4%的续航距离且材料成本降低了11.7%。陈萍等［11］从材料和结构两个方面提出电动飞机主驱动电机轻量化设计方法，对比相同结构参数的非晶合金电机和硅钢片电机的性能，在提升电机效率的同时使非晶合金电机整体减重了7.95%。

综上所述，相比于传统的解析及有限元优化设计，多目标优化算法优化设计在提高效率及准确度方面具有优势，已成为电机结构参数设计的趋势，且与传统硅钢等软磁材料相比，非晶合金材料在高频时铁耗较低，其在高频领域的应用效果优异［5］。然而，前人对非晶电机性能优化设计进行研究时未对不同优化算法进行比较，且未采用优化算法对电机做进一步拓扑结构优化，限制了电机效率及质量的优化效果［9-10］。鉴于此，本文以24 槽28 极永磁无刷直流电机为研究对象，采用铁基非晶合金为其定子铁芯材料，在建立电机性能计算解析模型基础上，结合基于材料特性建立的优化模型，以最高效率及最小重量为优化目标对比了不同优化算法对于电机模型的优化效果；随后，使用优化设计所得电机参数建立有限元模型，通过有限元计算验证优化设计的合理性，并基于有限元计算结果进一步进行拓扑结构优化。

1 非晶电机优化设计模型

1.1 非晶电机计算模型

图1 为24 槽28 极的永磁无刷直流电机结构示意图。由图可知，电机的永磁外转子结构具有转矩输出能力高、散热条件好等优点，可与铁基非晶合金材料Bs值和导热系数低于硅钢的材料［12］性能特点互补。而采用多极设计，可降低磁轭的厚度和机械强度的要求，便于后续质量优化。优化设计首先需对所研究电机建立解析计算模型，具体模型几何参数如图1 所示，这些几何参数之间关系可用以下方程来描述

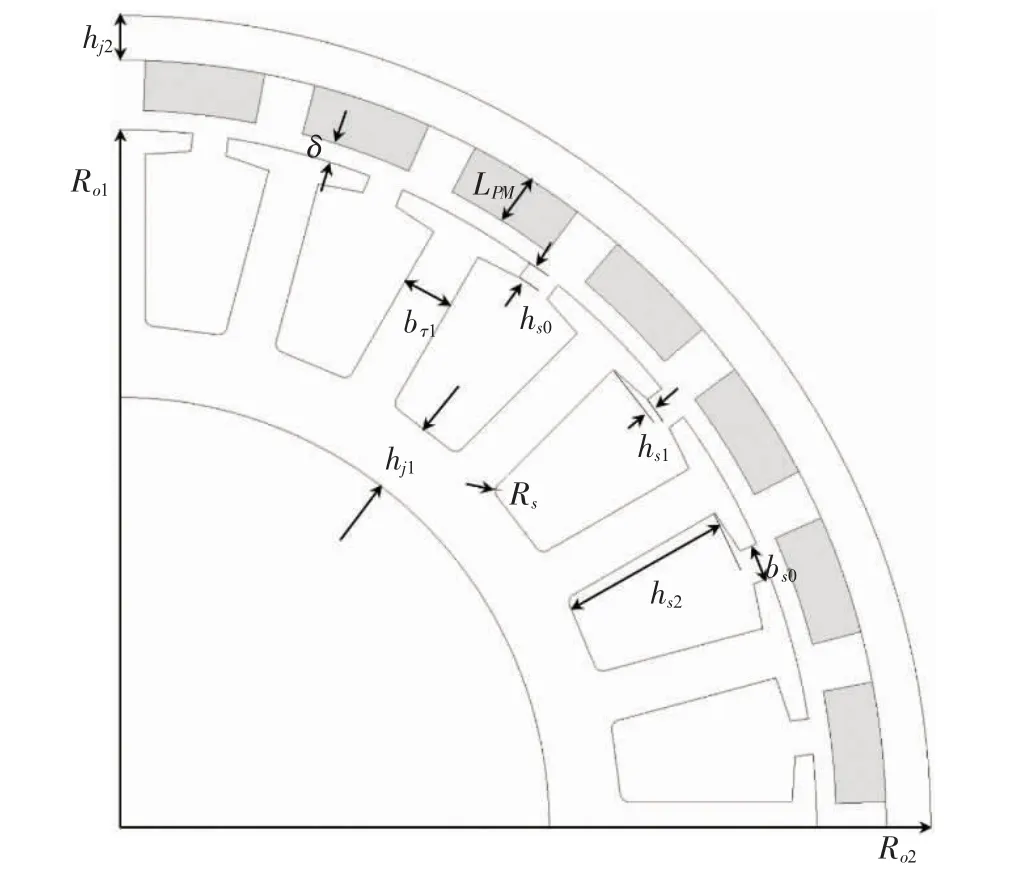
图1 永磁无刷直流电机结构及其解析模型几何参数示意图

其中，非晶电机的槽距τ1与极距τp可根据式（1）与式（2）得到，非晶电机最大输出转矩Tmax和电载荷A由式（3）及式（4）［13］来确定，Bδd为气隙磁密幅值，Lef为电枢计算长度，Ro1为电机定子外半径，a 为并联支路数，N 为绕组总匝数，I 为额定相电流有效值。

依据软磁材料的磁化特性，铁基非晶合金定子的齿部磁通量密度Bt1d、轭部磁通量密度Bj1d以及机壳转子轭部磁通量密度Bj2d可由下式分别计算［14］

其中，bτ1为定子齿宽，Kfe为铁基非晶合金材料叠压系数（依据工程经验取0.9），L1为定子铁芯叠压长度，hj1为定子轭部厚度，σ 为漏磁系数，αi为极弧系数，hj2为转子轭部厚度，L2为转子机壳长度。

电磁计算模型中，所计算的损耗分量主要为铁损和铜损，铁损通常用磁滞损耗Ph、涡流损耗Pe和附加损耗Pc表示。根据文献［15］，假设电流频率f 内的磁通量密度为正弦分布，则非晶定子齿部铁损Pt1d及轭部的铁损Pj1d可根据下式计算

其中，kh、ke分别为磁滞损耗系数、附加损耗系数；而涡流损耗如式中所示，根据非晶材料电导率ρfe及材料叠片厚度d 计算得出；Vt1d、Vj1d分别为非晶定子齿部及轭部的体积。

为保证后续优化设计结果合理，所得电机须满足以下要求：电机各部分避免出现磁路饱和；齿槽转矩小于额定转矩的10%；额定输出功率约为1.5 kW；额定转速3 000 rpm 以上。综合考虑所需设计非晶电机的运行速度、电负荷、槽满率、相电阻以及电机效率等参数，其中，几何参数优化过程中定子主要机械参数约束范围如表1 所示，电机主要磁路部分电磁参数约束如表2 所示。

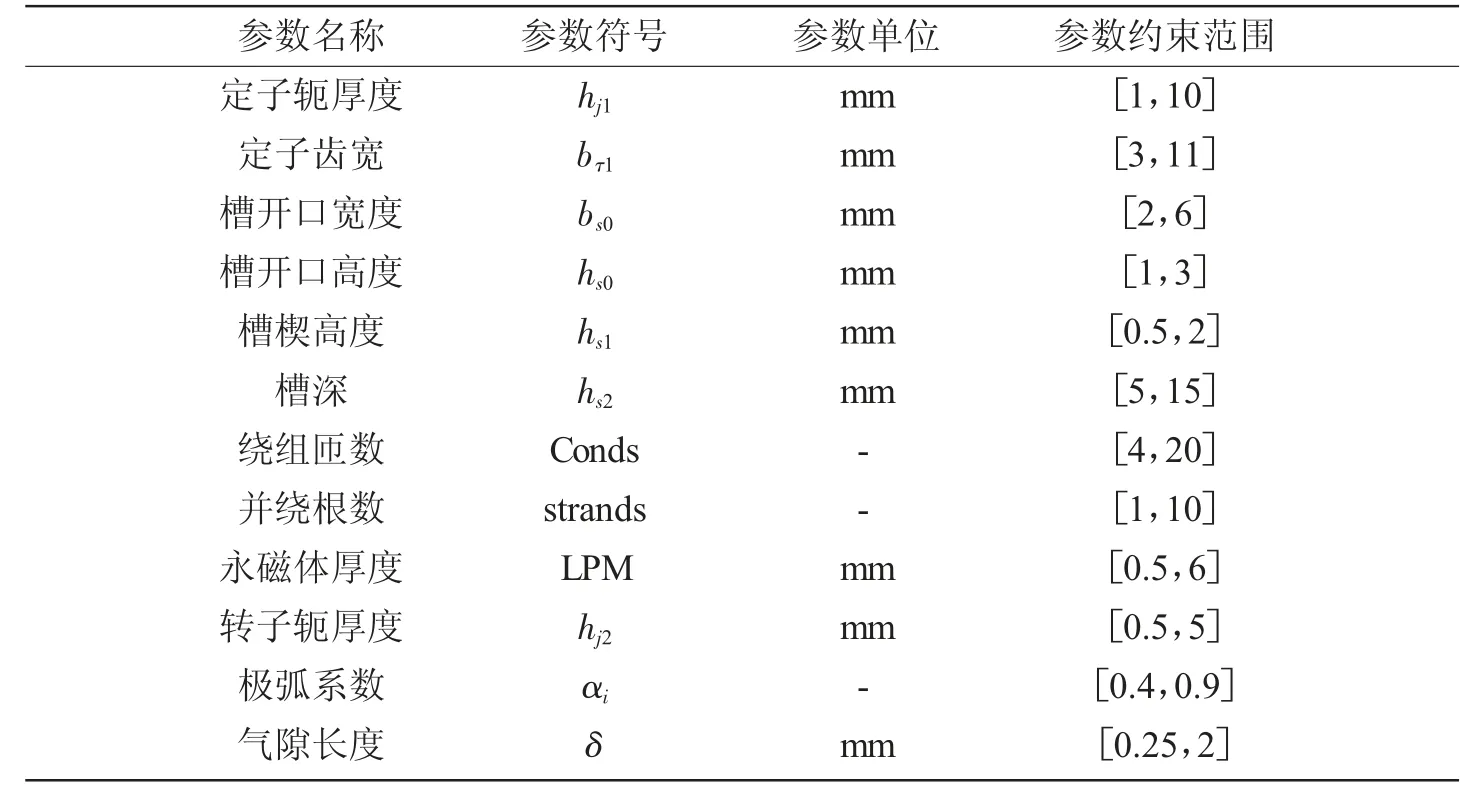
表1 定子主要机械参数约束范围

表2 电机主要磁路部分电磁参数约束

1.2 目标函数设置

对设计参数进行约束定义后，需确定优化问题和目标函数。针对本研究的非晶电机，需优化问题为：在满足性能要求前提下，使电机的效率尽可能高，质量尽可能小。其中，电机效率η 和电机质量M的定义分别为

其中，Pout、Pj2d、mfe、mpm、mcu、mroto分别为输出功率、转子铁损、非晶定子、永磁体、铜线和转子轭部质量。各部分质量等于各部分体积与各部分材料密度的乘积。则目标方程为

2 优化设计结果分析

在解析计算模型与目标函数确认后，建立基于优化算法的计算模型。所采用的优化算法包括：多目标遗传算法计算（MOGA）、粒子群优化算法（PSO）及自适应多目标算法（AMO）。图2 给出了上述三种优化算法计算所得帕累托边界收敛过程图。由图可知，所有算法都能找到一个关于所选参数的最优帕累托边界，其表示的是电机重量和效率之间权衡关系。这是由于当重量增加时，电机可设计为较低的电载荷及磁载荷，效率也就随之提高［16］。为此，图2 中提高电机效率的同时将导致其重量增加，且当效率提升至一定程度后，微小的效率提升都将导致电机质量的大幅度上升。对于MOGA 算法，由于计算时所搜索的目标区域较为集中，因而容易陷入局部最优解［17］，其所包含的帕累托解数量最多，有150 个帕累托解且连续性最强，但搜索范围较小。PSO 算法由于搜索范围更广，更不容易陷入局部最优解之中，其帕累托边界所包含的帕累托解数量较少，仅有22 个，搜索区域分布较为分散，也代表其搜索范围更广，且其精度不如多目标遗传算法。AMO 算法虽然计算点数最少，收敛较快，搜索范围较广，但其所给出的帕累托边界最为陡峭，且搜索趋势并不集中，在质量为2 kg 以内时，其所包含的帕累托解仅有9 个。

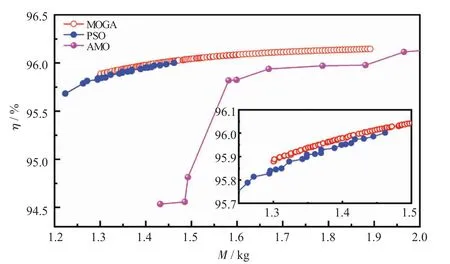
图2 不同优化算法的帕累托边界图

通过权衡效率与质量的关系，在三组帕累托边界中选择算法推荐的权重方案。表3 列出了三种不同优化算法下非晶电机尺寸参数优化设计结果。由表可知，MOGA 和PSO 算法的收敛速度较慢，均为计算到所设置的最大计算步数（20 000 步）时强制收敛，而AMO 算法的收敛速度较快，其在计算8 375 步后自行收敛。综合图2 及表3 结果还可知，利用MOGA 算法得到了最佳非晶电机效率以及最佳的权重方案，但计算效率较低；通过PSO 算法可得到最小非晶电机重量方案，但其最终结果在效率与质量方面均无明显优势，且其解集可认为被多目标遗传算法的计算结果解集所支配；AMO 算法仅在计算速度方面具有明显优势。

表3 不同优化算法下非晶电机尺寸参数优化设计结果

3 优化模型的有限元验证

为验证上述三种不同优化算法结果的合理性，基于Maxwell 有限元软件，采用表3 中所列的不同优化算法下非晶电机尺寸的优化参数建立了有限元模型。其中，为保证计算结果的准确性和稳定性，在进行有限元计算前，需要进行合理的建模和预处理。在非晶电机有限元计算过程中，假设以下条件以简化计算。

（1）由于使用二维电机截面进行计算，因此忽略非晶电机的端部漏磁问题，且只考虑z 轴分量磁矢位Az；

（2）为了简化计算，通常会忽略铁芯的饱和效应，且忽略电机的温度效应，假设电机的温度保持75 ℃不变；

（3）在电机磁化过程中，由于磁介质的磁滞特性，会导致磁场和磁势之间的关系是非线性的。为简化计算，忽略磁滞效应，假设磁场和磁势之间为线性关系；

（4）在电机运行过程中，由于磁场的变化会在导体中激发涡流，从而消耗能量，但本模型中，铜线截面积较小，线圈内的涡流损耗极小，计算中忽略。

综合以上假设，本研究中非晶电机的二维有限元瞬态模型的边值问题满足下式［14］

其中，Ω 表示非晶电机的总体求解区域；Az为磁矢位；S1表示第1 类边界条件，即电机转子外圆和定子铁芯内圆；S2为第2 类边界条件，在本研究的模型中代表永磁体内表面圆弧；μ 表示材料的磁导率；σ 表示材料的电导率；t 表示时间步长；Jz、Js分别表示轴向电流的面密度及永磁体区域等效面的电流密度（A/m2）；μ1、μ2为S2两侧的部件材料磁导率。图3 给出了有限元计算模型边界条件及网格剖分。

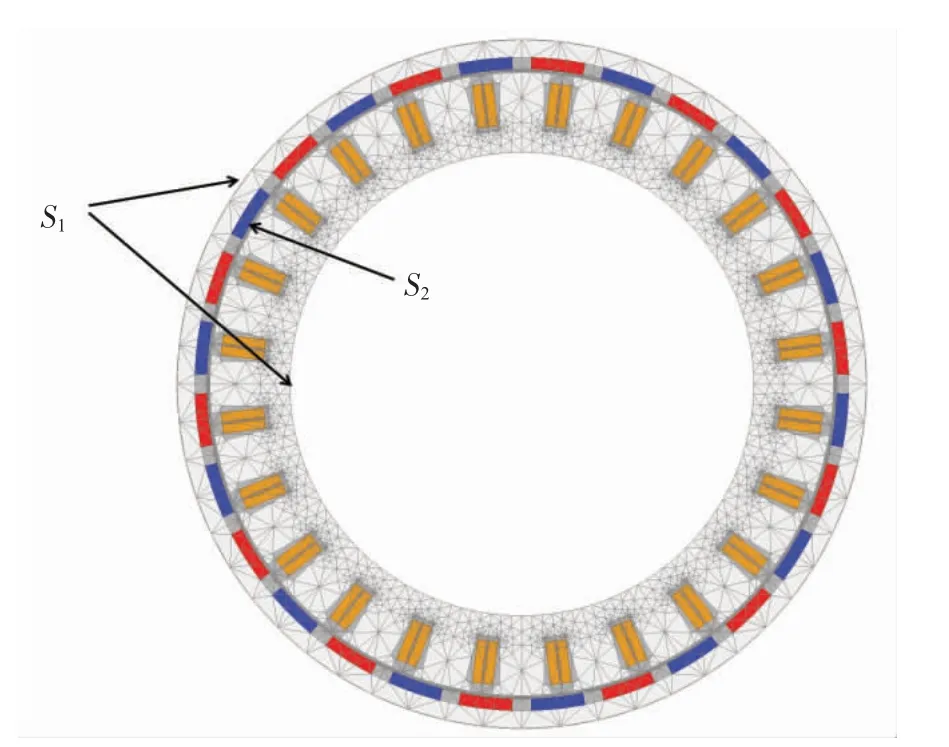
图3 有限元分析网格及边界条件

图4 给出了三种不同优化算法下非晶电机二维横截面有限元负载磁密云图。由图可知，额定负载工况下，定子轭部磁密幅值小于1.21 T，齿部磁密幅值小于1.62 T，绝大部分区域磁密低于1.26 T。由三种方案磁密云图，可知总体磁密处于合理范围内，且磁密较小（绝大部分区域磁密低于0.8 倍Bs），留有较大的过载空间。由此可知，采用MOGA、PSO 与AMO 三种不同优化算法设计的铁芯负载磁密均分布合理。

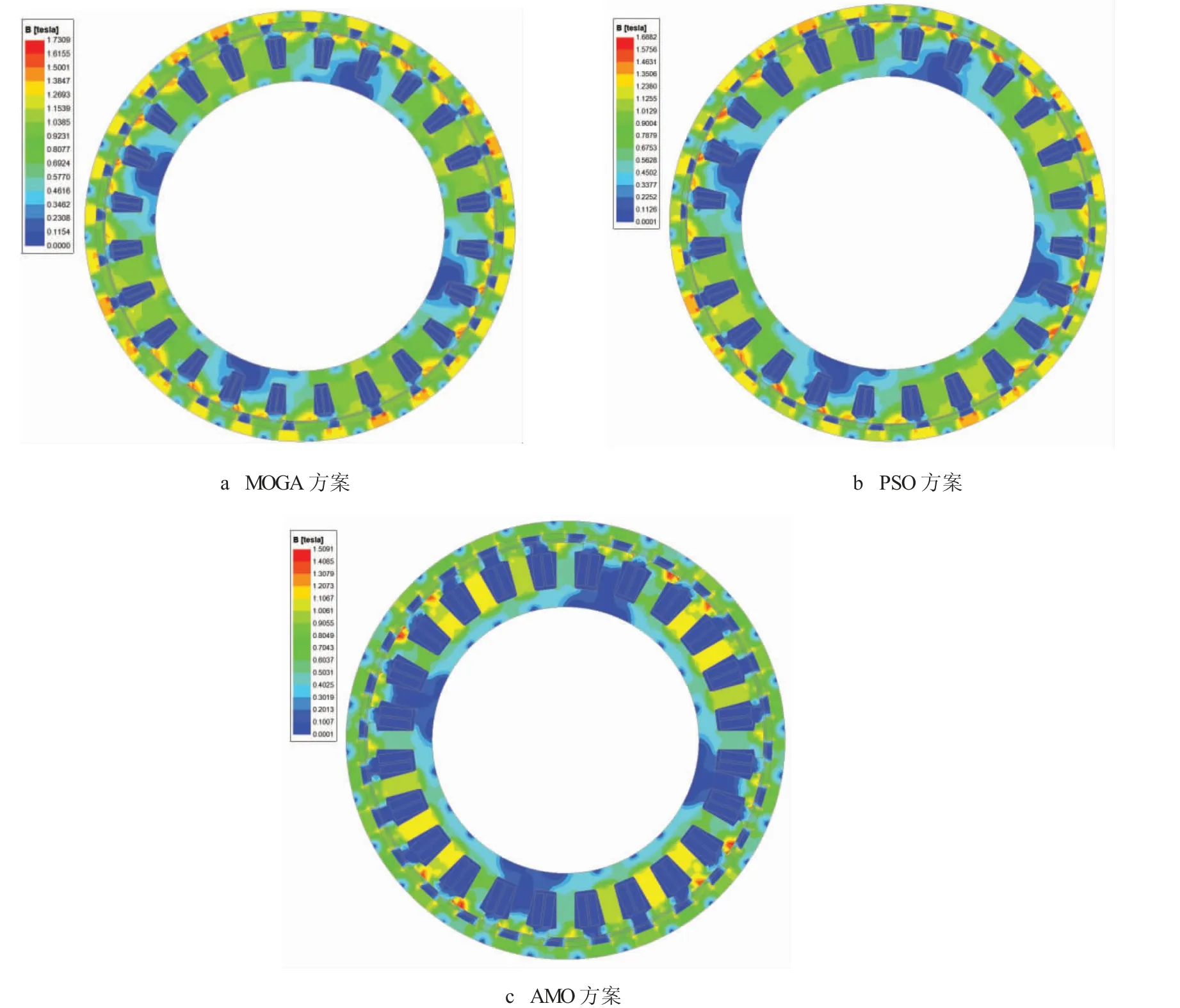
图4 不同优化算法方案非晶电机二维横截面有限元负载磁密云图

表4 列出了采用不同优化算法设计的与使用有限元计算的转速、扭矩及效率结果对比情况。由表可知，优化算法设计结果和有限元分析结果之间有很好的一致性，相对误差范围仅在5%以内。这也进一步验证了优化算法设计结果的合理性。同时考虑到MOGA 算法可获得更高的电机效率（如表3 所示），后续的非晶电机拓扑结构优化选择MOGA 算法为最佳权重算法。

表4 优化算法设计与有限元计算的转速、扭矩及效率结果对比情况

4 拓扑结构的优化

由图4a 可知，MOGA 方案定子轭部与转子轭部上存在磁密极低的点位。其中，低磁密点位位于磁路的交接转角处。为此，可将此处的铁磁材料去除，若对磁路及非晶电机性能影响甚微，则可达到从拓扑结构上对电机实现轻量化的目的。图5 给出了非晶电机拓扑结构优化图。

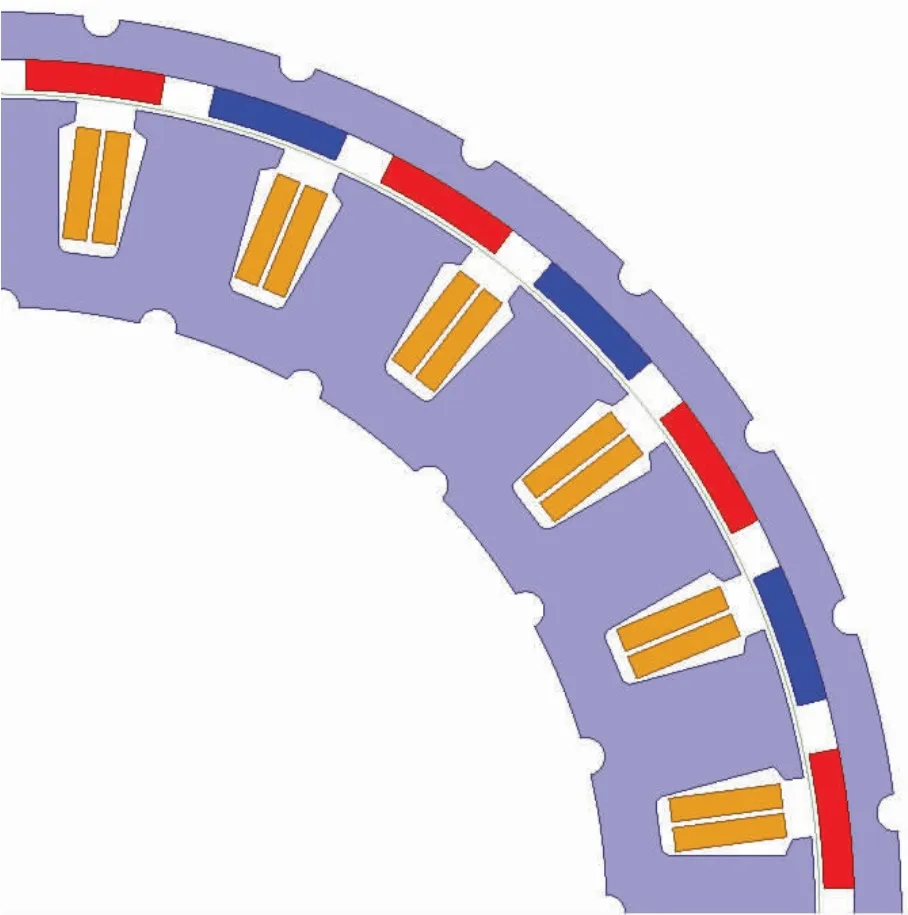
图5 非晶电机拓扑结构优化示意图

图6 为非晶电机拓扑结构优化后二维横截面有限元负载磁密云图。其中，定、转子开槽半径选择均为1 mm。与图4a 结果对比可知，转子轭部最大磁密由1.73 T 上升至1.75 T，仅上升0.02 T，仍未超过转子轭部材料饱和磁密1.84 T。定子轭部最大磁密由1.27 T 上升至1.28 T，仅上升0.01 T，定子齿部磁密幅值低于1.62 T，定子绝大部分磁密低于1.28 T，定子未出现过饱和现象，非晶电机仍有充足过载空间。

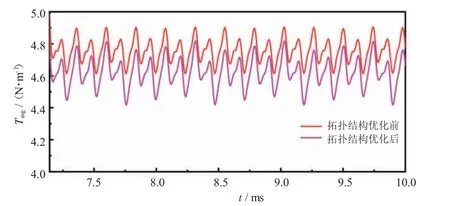
图6 最终优化方案的二维横截面有限元负载磁密云图

图7 给出了非晶电机拓扑结构优化前后负载输出转矩曲线对比情况。由图可得，拓扑结构优化后，非晶电机输出转矩略有降低，由4.75 N·m 降低至4.62 N·m，降低了1.26%；转矩脉动增加了60 mN·m，转矩脉动占额定扭矩比重由7.8%上升至9.3%，上升了1.5%。

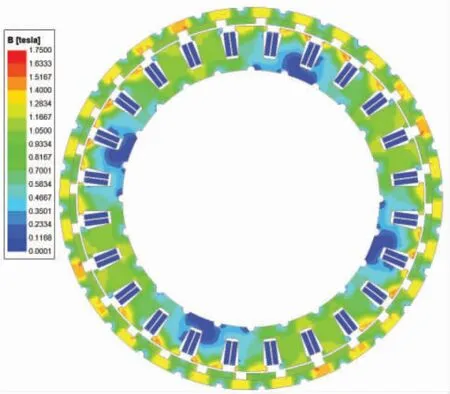
图7 非晶电机拓扑结构优化前后负载输出转矩曲线对比

综上所述，得出拓扑结构优化后，转矩脉动为9.3%，符合转矩脉动低于10%的性能要求；负载工况下定子磁密幅值低于1.62 T；输出转矩仅下降1.26%；拓扑结构优化后的电机负载性能仍符合要求，从负载性能角度拓扑结构优化的合理性。表5 给出了非晶电机拓扑结构优化前后有限元计算所得非晶电机效率与定、转子质量对比。由表可知，经过拓扑结构优化，定子重量减少了2.0%，转子轭铁重量减少了5.6%，非晶电机效率提升了1.02%，相比于输出转矩的下降，减重及效率提升效果更为显著。

表5 初始方案及最终优化方案有限元计算所得电机效率与定、转子质量对比

5 结论

本文以24 槽28 极永磁无刷直流电动机为研究对象，以提高电机效率和降低电机质量为目标，采用了MOGA、PSO、AMO 三种优化算法搭建了参数化的磁路法电机计算模型，并结合有限元模型的验证，对非晶电机的12 个结构参数进行优化设计，主要结论如下所述。

（1）基于解析计算模型得出的优化结构参数，使用MOGA、PSO 及AMO 算法对非晶电机进行了优化设计。帕累托边界图结果表明，MOGA 计算时其所搜索的目标区域较为集中，计算最为精确但易陷入局部最优解；PSO 搜索区域分布较为分散，其搜索范围较MOGA 更为宽广；AMO 计算点数最少，收敛最快但精度最低。

（2）通过MOGA、PSO 以及AMO 算法优化的非晶电机质量与电机效率依次分别为：1.33 kg 和95.75%，1.27 kg 和95.24%，1.49 kg 和94.36%。鉴于MOGA 优化的方案效率最高且其质量较PSO 算法得出的仅重0.06 kg，为此选用MOGA 算法作为最佳权重计算方案。

（3）结合有限元模型，对三种不同算法优化设计所得的非晶电机空载与负载特性进行了验证和比较。结果表明，基于不同算法的优化结果和有限元分析结果具有较好的一致性，各项性能参数相比误差范围均在5 %以内。其中，经有限元分析验证可知，MOGA、PSO 及AMO 算法的电机效率依次为93.79%，92.54%和94.16%。

（4）采用有限元模型对MOGA 算法优化的非晶电机做进一步的拓扑结构优化。与优化前相比，非晶电机定子和转子轭铁质量分别减少了2.0%和5.6%，电机效率提升了1.02%至94.81%。