凹角外问题非重叠区域分解算法的自适应研究

蔡文璐，刘保庆

（南京财经大学 应用数学学院，江苏 南京 210023）

在求解和研究无界区域的偏微分方程问题时，区域分解算法有着广泛的应用［1-5］。但是，当面对具有间断解或大梯度解的偏微分方程问题时，均匀网格产生的误差可能会很大，为了提高解的精度，自适应方法则可以根据偏微分方程的特点进行剖分［6-9］。本文在非重叠型区域分解算法的基础上，提出了无界凹角区域上各向异性偏微分方程的自适应研究。

1 问题描述

设Ω 是具有光滑边界、简单的无界区域，∂Ω=Γ1∪Γ∪Γ2，其中

Γ2=｛（r，θ）│r=a，θ=ω）｝，考虑如下边值问题

设b>a>0，区域Ω，边界Γ1，Γ2，Γ 用极坐标可以表示成

其中，（r，θ）为极坐标，它与直角坐标（x，y）的关系如下

下面为了将各向异性问题转化为线性问题进行讨论，作如下变量变换

则Γ 上任一点（ξ，η）处的单位外法方向为

于是Dirichlet 边值问题（1）转化为如下调和问题

引入椭圆坐标（μ，φ），它与坐标（ξ，η）的关系如下

通过Fourier 级数展开法可得到如下Poisson 积分公式和自然积分公式

2 D-N 算法以及变分问题

作半径为R'的圆弧Γ'包围Γ，外区域Ω 被分为两个部分：有界区域Ω1和无界区域Ω2，具体如图1所示。

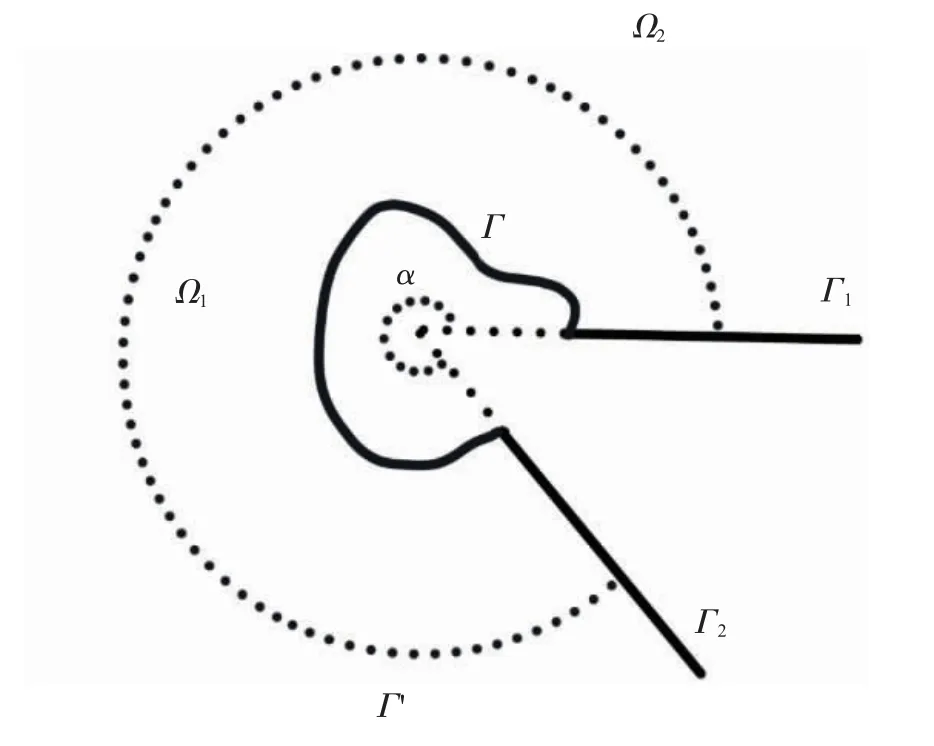
图1 D-N 交替算法求解区域

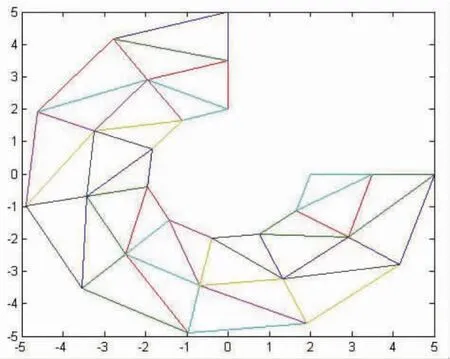
图2 9*2 的均匀网格

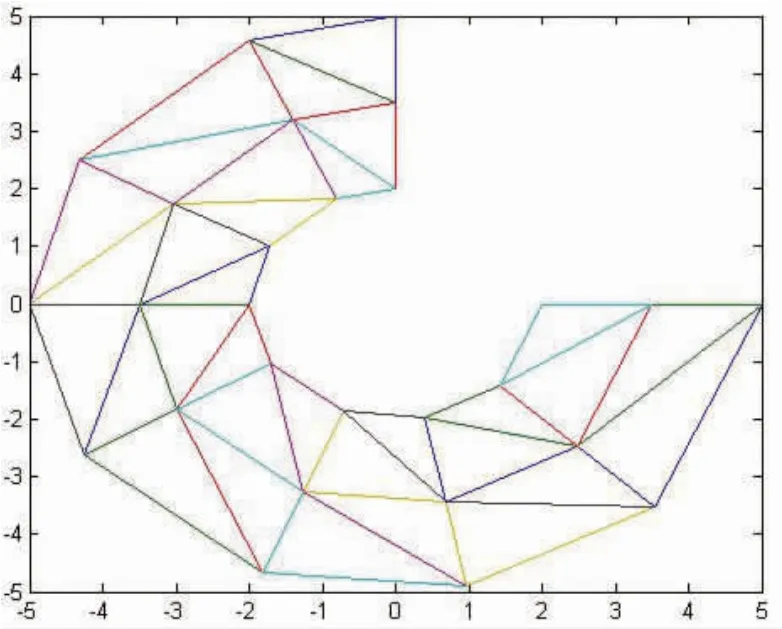
图3 9*2 的移动网格

D-N 算法的定义如下：

步骤4：计算或输入松弛因子δk，并在Γ'上令+（1-δk）λk。

步骤5：k=k+1，继续步骤2 的计算。

将圆弧Γ'分为N 份，并在Ω1中进行有限元剖分，可以得到D-N 交替算法的离散化格式。

3 收敛性分析

离散D-N 算法的迭代过程可以写成

定理1 离散D-N 算法（5），（6）与预处理Richardson 迭代法等价。

预处理Richardson 迭代法构造如下

定理3 当0＜min δk≤max δk＜1 时，离散D-N 算法均收敛，且收敛速度与h 无关。

4 自适应算法与数值例子

自适应算法有很多种，本文将运用移动网格方法。为了提高解的精度，通过控制函数将节点移动到解需要精确逼近的地方,所以自适应算法相比一般的均匀网格剖分具有高效率高精度的特点。

由表1、2 可知，迭代序列是几何收敛的；数值解与精确解的误差随着剖分网格的加密而降低；无论网格粗细，收敛速度大致相同，说明D-N 算法的收敛速度与网格参数无关，这与第3 节的定理结论一致；移动网格下的数值解与精确解的误差比均匀网格下的小，说明移动网格的数值解的精度比均匀网格的更高。

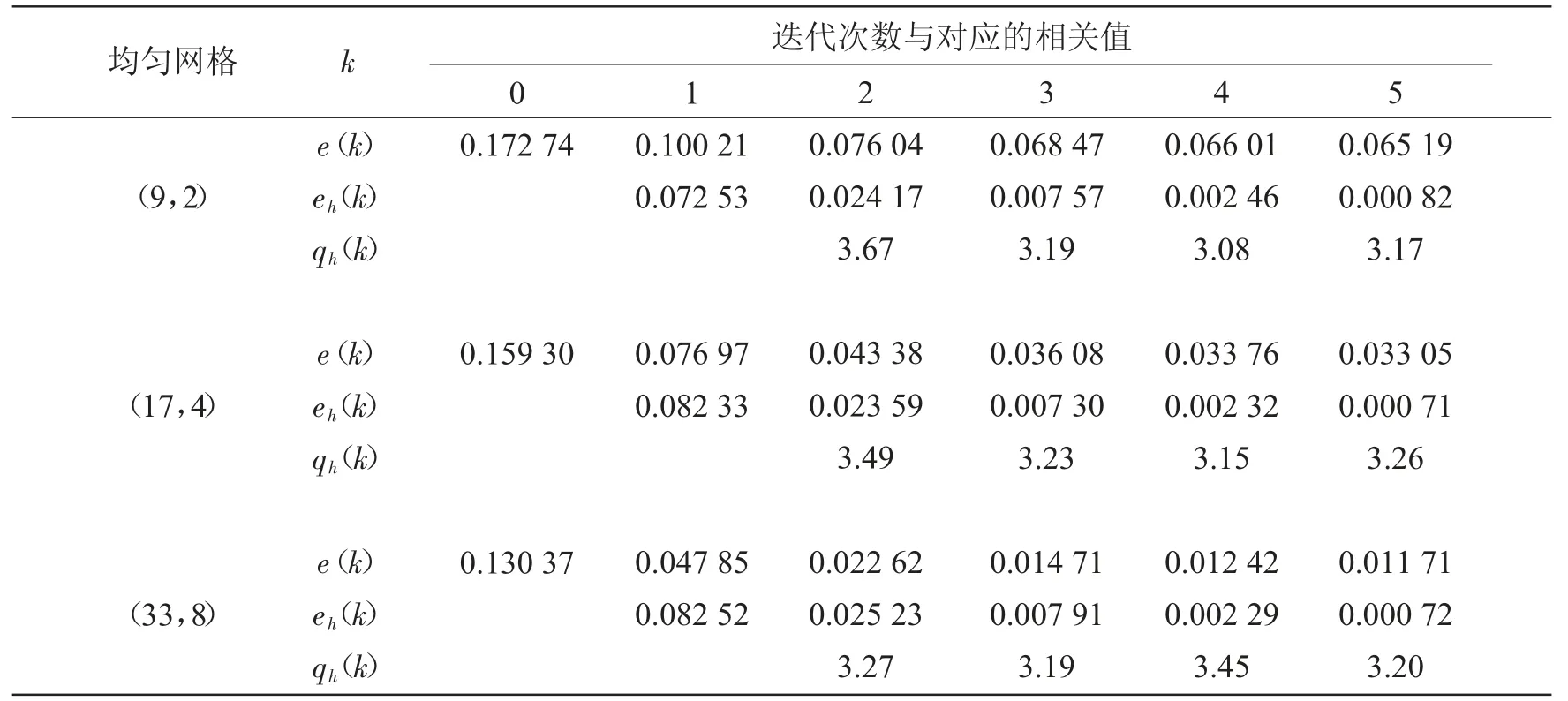
表1 均匀网格中误差与网格的关系

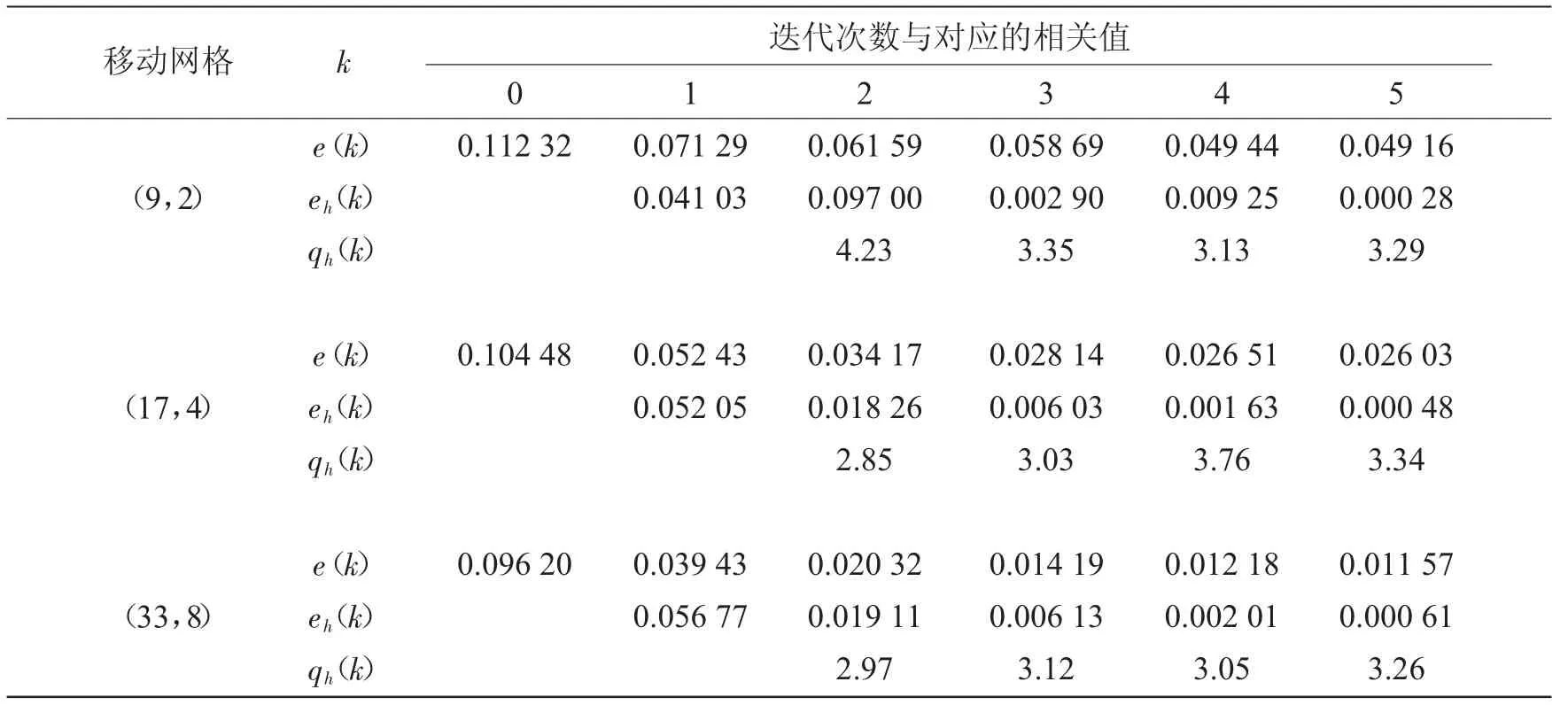
表2 移动网格中误差与网格的关系