异构无人集群分组编队自适应跟踪-合围控制
张 毅, 于 浩, 杨秀霞, 姜子劼
(海军航空大学航空作战勤务学院, 山东 烟台 264001)
0 引 言
随着分布式作战、马赛克战等前沿作战理论的提出,无人集群系统成为世界各国研究新型作战样式的重要武器平台。由无人机(unmanned aerial vehicle,UAV)和无人车(unmanned ground vehicle,UGV)组成的空地协同作战系统,在协同探测、侦测等任务场景中发挥了重要作用。UAV具有侦察范围广、机动能力强的优势,作为通信中继,可通过伴飞侦察为UGV提供精准的环境信息,能够克服不利地形对地面车辆的影响,显著提升了作战效能。
编队控制是实现集群系统协同的基础,通过控制协议的设计,使智能体按照预定的时变队形形成期望的相对阵位关系,执行特定任务[1-3]。合围控制由传统的编队控制问题衍生而来,在确保部分智能体(领导者)形成期望队形的同时,还使其余智能体(跟随者)的状态或输出收敛至领导者形成的凸包内[4]。在目标跟踪等典型任务场景中,领导者和跟随者除了需要形成预设的编队合围构型外,还需跟踪目标的运动轨迹,由此便催生了更为复杂的跟踪-合围控制问题[5-6]。
研究跟踪-合围控制问题的大多数文献中,一般将目标视为“自治系统”[7-10],即不考虑目标的机动行为。而在执行对非合作目标的合围任务时,目标往往通过改变机动形式实时调整期望轨迹,来摆脱集群系统的跟踪。文献[11]针对具有未知输入目标的跟踪-合围控制问题,设计了分布式控制协议,利用光滑的非线性函数有效抑制时变输入的影响;文献[12]提出一种双层编队跟踪-合围控制策略,给出控制参数选取的具体算法,并基于移动机器人验证方案的可行性。
上述文献的研究对象均为同构集群系统,即智能体具有相同的动力学模型和状态维度,利用克罗内克尔积可直接对集群系统进行状态维度的扩展,进而得到系统稳定的可行性条件;而对于可以发挥互补优势的异构集群系统来说,模型及状态维度的显著差异使得传统的线性齐次分析方法不再直接适用,无法为跨区域、多维度的复杂任务提供有效的解决方案。随着研究的深入,国内外学者基于输出调节和状态调节两种策略,对异构集群的合围问题进行研究。文献[13]分别构造静态和动态输出反馈控制协议,解决了同构和异构集群系统的时变输出合围控制问题;文献[14]结合观测器理论和事件触发机制设计控制律,使集群系统实现输出合围的同时避免了智能体之间的连续通信;文献[15]利用动态补偿技术,将合围控制问题转化为多智能体系统的输出调节问题,提出一种分布式动态自适应状态反馈和自适应输出反馈控制协议。
需要指出的是,在执行如多目标探测、合围等分布式作战任务时,仅靠单一编队难以解决问题,此时需要将集群系统分为多个小组,通过组间的协同配合共同完成任务。目前,解决异构集群系统分组合围问题的研究成果尚未见报道。文献[16]研究了同构集群系统的分组合围控制问题,提出完全分布式的控制协议,并将其应用到多机器人系统;文献[17]在文献[11]的基础上推导得到分组编队间拉普拉斯矩阵的耦合性质,实现了对多目标的分组合围。
受上述研究成果的启发,本文研究了目标控制输入未知情形下异构集群系统分组编队的跟踪-合围控制问题。集群系统中的智能体分为目标、领导者和跟随者,控制目标是使领导者以期望输出队形按预定分组跟踪目标,同时跟随者以期望输出队形收敛至所属分组内的领导者输出形成的凸组合,间接实现对目标的分组合围。本文主要贡献有:
(1) 领导者和跟随者的期望输出队形均是时变的,每个智能体的动力学模型和状态维度均是异构的,且目标均具有未知控制输入;
(2) 基于节点和通信边的自适应控制方法,分别为领导者和跟随者设计分布式观测器,利用邻接信息估计目标和领导者状态的同时,实现对时变控制输入的动态补偿,并给出观测器收敛的充分条件;
(3) 利用Luenberger观测器估计智能体自身状态,并基于状态估计值和输出调节策略,设计分组跟踪-合围控制律,避免了对拉普拉斯矩阵特征值的显式计算,并给出异构无人集群实现分组跟踪-合围的充分条件。
1 问题描述和模型建立
1.1 问题描述
异构集群系统中各类智能体因动力学模型或分配任务的不同,使得工作空间或外部环境存在较大差异,而通过不同智能体之间的相互通信、自主协调,可以并行解决问题,显著提高作战效能。例如,受地球曲率的影响,无人艇的探测距离相对受限,无法直接获取视距外目标的状态信息,对此引入多架UAV作为通信中继,可以为前者提供丰富的环境信息,大幅提升集群系统的安全性和探测的精度;在野外执行任务时,UGV易因高山、树木的遮挡,而使通信和探测能力受到制约,此时需要探测能力强的多UAV系统提供第三视角,提高UGV行驶工况的稳定性和安全性同时,实现对目标的跟踪。
结合图1,解释说明本文空地异构协同跟踪的任务背景及控制目标。图中目标设定为在地面移动且输入未知的智能体,领导者表示执行空中伴飞侦察任务的UAV,跟随者表示UGV。为此本文的控制目标确定为:通过控制协议的设计使多UAV根据预定分组形成期望队形跟踪目标,同时使UGV以期望队形收敛至多UAV形成的凸包投影内部。由于空中UAV完成对目标的跟踪后,将以地面目标为中心建立期望队形,而UGV又以多UAV状态的加权值作为编队中心形成期望队形,据此可以确保UGV间接实现了对目标的合围。

图1 UAV-UGV异构集群系统协同目标跟踪Fig.1 Cooperative target tracking of UAV-UGV heterogeneous swarm system
1.2 模型建立
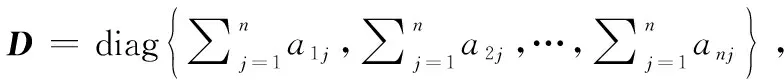
假设异构无人集群系统包括p个目标、N个领导者和M个跟随者。其中,领导者和跟随者的模型[18-19]可描述为
(1)
式中:i=1,2,…,N,…,N+M,xi(t)∈Rni、yi(t)∈Rl和ui(t)∈Rmi分别表示智能体的状态、输出和控制量;Ai∈Rni×ni、Bi∈Rni×mi和Ci∈Rl×ni分别表示系统矩阵、输入矩阵和输出矩阵。其中,(Ai,Bi)是可控的且(Ci,Ai)是可测的。目标的模型为
(2)
式中:j=1,2,…,p,vj(t)∈Rm、sj(t)∈Rl和rj(t)∈Rr分别表示目标的状态、输出和控制量;AT∈Rm×m、BT∈Rm×r和CT∈Rl×m分别表示系统矩阵、输入矩阵和输出矩阵。其中,(AT,BT)是可控的且(CT,AT)是可测的。
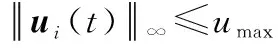
假设2异构集群系统包括p个分组且满足:① 每个分组中均存在以目标为根节点的有向生成树;② 领导者之间可进行跨组通信;③ 跟随者只能接收本组领导者的信息,并与其邻居跟随者是双向通信的,且不存在孤立领导者;④ 目标相对独立,仅向领导者发送信息而不接收信息。
根据假设2,集群系统的拉普拉斯矩阵可表示为
(3)
式中:LET∈RN×p表示目标到领导者的通信;LE∈RN×N表示领导者之间的通信;LF∈RM×M表示跟随者之间的通信;LFE∈RM×N表示领导者到跟随者的通信。
结合假设2可进一步将LE分解为
(4)

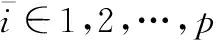
假设4[20]对于领导者i=1,2,…,N,调节器方程:
(5)
有对解(Xi,Ui),且矩阵方程:
BiRi-XiBT=0
(6)
存在解Ri。
假设5[20]对于跟随者j=N+1,N+2,…,N+M,调节器方程:
(7)
有对解(Wji,Yji),且矩阵方程:
Bjφji-WjiBi=0
(8)
存在解φji。
由于异构集群系统状态维度的差异,无法直接利用智能体的状态信息进行控制器的设计,为此利用假设4和假设5中的调节方程进行输出维度的统一。
分别设时变向量hi(t)、δj(t)为领导者和跟随者的期望时变输出队形,hi(t)和δj(t)是可微的,且分别满足输出方程hEi(t)=Cihi(t)和δFj(t)=Cjδj(t)。

(9)
则称领导者实现以期望输出队形hEi(t)跟踪目标。

(10)

定义3若定义1和定义2同时成立,则称异构无人集群系统实现了对多目标的分组跟踪-合围。

2 控制律设计与稳定性分析
为实现上述控制任务,本节分别针对领导者和跟随者进行控制律设计。
2.1 跟踪控制律设计

ηBTfi(ζi(t))
(11)
(12)

在分布式观测器式(11)中,自适应增益ci(t)的引入,使得在进行状态估计的过程中,同步进行邻接估计误差的实时反馈和补偿,实现状态估计的自调节,能够提高状态估计的精度和观测器的收敛速度。
为使领导者形成期望队形并实现对目标精确跟踪,设计如下控制协议:
(13)
wi(t)-ηϑi(t)
(14)
在观测器中,设计了基于节点的自适应补偿增益,使得对目标的邻接估计误差能够进行实时反馈,提高了集群系统的跟踪性能。
引理 1[17]在假设2成立的条件下,对于含组间通信耦合的LaplacianLE,存在实对角矩阵Δ1和G使不等式成立:
(15)
为实现领导者对目标的分组跟踪,控制协议式(11)~式(14)中的部分参数需满足:

(16)
式中:Q>0。
(2) 选取(Xi,Ui)、Ri使假设4成立,设计Ei、K1i使Ai+EiCi和Ai+BiK1i是Hurwitz的,K2i满足K2i=Ui-K1iXi。
(3) 非线性函数fi(ζi(t))、ϑi(t)定义为
(17)
ϑi(t)=RiGi(t)
(18)
式中:
(19)

(4) 存在正定矩阵Mi,满足方程:
Mi(Ai+BiK1i)+(Ai+BiK1i)TMi+2Ini=0
(20)
(5) 选取控制输入抑制参数:η>rmax。
下面给出异构无人集群系统实现分组编队跟踪控制的充分条件。
定理1若假设1~假设5成立,控制律中的参数满足式(16)~式(20)且期望队形的补偿函数wi(t)满足:
(21)
则异构集群系统在控制协议式(11)~式(14)的作用下,实现了分组编队的跟踪控制。

η(IN⊗BT)f(ζ(t))-(IN⊗BT)rT(t)
(22)
式中:
ζ(t)=[ζ1(t),ζ2(t),…,ζN(t)]T
c(t)=diag{c1(t),c2(t),…,cN(t)}
ρ(t)=diag{ρ1(t),ρ2(t),…,ρN(t)}


(23)
结合式(22)可得
η(LE⊗BT)f(ζ(t))-(LE⊗BT)rT(t)
(24)
构造具有如下形式的Lyapunov函数,
(25)

(26)
式中:
2ζT(t)[(c(t)+ρ(t))Δ1GLE⊗PBT]rT(t)-
2ηζT(t)[(c(t)+ρ(t))Δ1GLE⊗PBT]f(ζ(t))
(27)
根据f(ζ(t))定义并结合Cauchy-Schwarz不等式可得
-2ηζT(t)[(c(t)+ρ(t))Δ1GLE⊗PBT]f(ζ(t))≤
(28)
根据假设1有
-2ζT(t)[(c(t)+ρ(t))Δ1GLE⊗PBT]rT(t)≤
(29)
综上可得
(30)
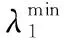
(31)

(32)

下面证明领导者在控制律的作用下能够实现以期望队形跟踪目标。
将控制律代入系统方程可得

(33)
对ξi(t)求导可得:
(34)
构造具有如下形式的Lyapunov函数:
(35)
沿式(35)求导得到:
(36)

(37)


(38)
由此可得

(39)

故领导者最终能够以期望输出队形跟踪上目标。
证毕
2.2 合围控制律设计
在实际任务背景下,因外部环境的限制,跟随者无法直接获取目标的状态信息,因此需要领导者作为中介,间接“传递”目标状态。在第2.1节中,领导者以目标为中心形成期望队形,则只需保证跟随者以期望的输出队形在控制协议的作用下收敛至领导者输出的凸组合,即可完成跟随者对于目标的输出合围。
(40)
(41)
(42)
式中:
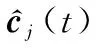
与观测器式(11)不同,式(41)中设计基于通信边的自适应增益,实现估计误差实时反馈的同时,便于后续Lyapunov函数的设计和闭环系统稳定性的分析。
为实现跟随者对目标的分组合围,控制协议式(40)~式(42)中的部分参数需满足:

(2) 非线性函数fj(t)、κji(t)定义为
(44)
(3) 存在正定矩阵Mj,满足方程:
Mj(Aj+BjK1j)+(Aj+BjK1j)TMj=-2Inj
(45)
(4) 选取控制输入抑制参数:
η1>umax
(46)
下面给出异构无人集群系统实现分组合围的充分条件。
定理2若假设1~假设5成立,且控制参数满足上述条件且编队辅助函数满足可行性条件:
(47)
则跟随者在控制协议式(40)~式(42)的作用下以期望队形收敛至领导者输出的凸组合。
证明首先证明观测器的收敛性。定义跟随者对领导者的估计误差为


(48)
定义具有如下形式的Lyapunov函数:
(49)
对式(49)求导可得
(50)
式中:
(51)
根据fj(t)的定义及假设1可得
(52)
且
(53)
结合式(46),据此可将式(50)化简为
(54)

(55)

(56)
令

证毕
将控制律式(42)代入系统方程可得
(57)

(58)
根据式(47)及假设5化简得
(59)
设计如式(60)所示的Lyapunov函数:
(60)
求导得
(61)
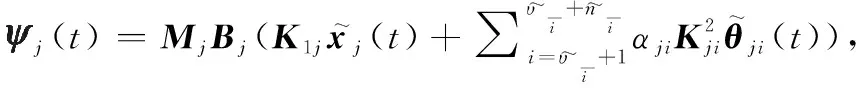

(62)

(63)
故可将式(61)化简为

(64)

证毕
综上,异构集群系统能够在控制协议的作用下实现分组编队的跟踪-合围控制。
上述控制协议的设计是针对多目标的跟踪与合围问题展开的,适用于目标空间位置较为分散的情形。而当多个目标空间位置较为集中时,无需对异构集群系统进行分组设计, 此时本文研究的问题便转化为单一编队对目标的跟踪-合围控制问题,领导者对目标状态的估计转化为
ηBTfi(ζi(t))
(65)
(66)
(67)

(68)
定义估计误差:
(69)

(70)
(71)
ζ(t)-η(LE⊗BT)f(ζ(t))-(-LET⊗BT)rT(t)
(72)
后续证明过程与定理1类似。与分组编队不同,在此情形下观测器的期望值为目标状态的加权值,即所有领导者都以多目标状态的凸组合为编队中心,并在控制协议的作用下形成期望队形,实现了对目标的跟踪控制,跟随者的控制策略与前文类似。相较于文献[23],本文的运动目标具有未知的控制输入,而非传统的“自治系统”,需在观测器及控制律的设计中利用非线性函数对rT(t)进行抑制。
3 仿真验证
3.1 仿真场景构建
为验证本文控制策略的有效性,本节考虑由12架UAV、9辆UGV组成的空地异构无人集群系统共同执行对3个机动目标的跟踪-合围任务,其中领导者i=1,2,…,12表示UAV,跟随者j=1,2,…,9表示UGV。考虑实际任务背景下,受限于高山或其他建筑物的遮挡,UGV无法利用自身携带的传感设备探测地面机动目标的具体方位,此时需要UAV作为通信中介在空中形成期望编队,并确保目标处于UAV队形在地面的投影内,同时UGV以期望输出队形跟踪UAV输出的凸组合,进而间接实现了UGV对地面目标的合围。
考虑如下目标模型:
在本文研究的跟踪-合围问题中,重点关注智能体之间的位置关系,且由于目标在XOY平面内运动,因此仅考虑UAV在定常高度下飞行,基于文献[24]中位置环的控制架构,给出UAV线性化模型
利用反馈线性化理论,基于麦克纳姆轮结构的UGV模型[25]可表示为
Aj=02×2,Bj=I2,Cj=I2
3.2 仿真参数设置
假设在初始阶段t取0~30 s,目标沿同一方向运动,此时异构智能体构成单一编队进行合围,智能体间的通信关系如图2(a)所示,目标的控制输入设定为

图2 集群通信拓扑 Fig.2 Swarm communication topology
目标初始运动状态设定为:v1(0)=(1,0,2,0),v2(0)=(3,0,2,0),v3(0)=(2,0,2,0)。
为直观描述异构集群系统的控制效果,分别设计UAV、UGV的编队函数为
为使UGV以期望输出队形跟踪UAV输出的凸组合,设置权重αji=1/12,即,将UAV输出的平均值作为UGV期望编队的中心。智能体的初始状态随机给出。
下面对控制策略中的参数值进行设计。

取Q=0.5I2,求解Riccati方程得
求解Lyapunov方程得
根据编队可行性条件求得编队辅助函数:
wi(t)=
wj(t)=
假设各目标在t取30~60 s进行分散机动,为实现分组合围,智能体间的通信拓扑切换为图2(b)所示的结构,控制输入调整为
r1(t)=[0.8sin(0.06t),0.8cos(0.04t)]
r2(t)=[0.5sin(0.06t),0.8cos(0.05t)]
r3(t)=[0.3sin(0.06t),0.8cos(0.06t)]
UAV和UGV按预定分组继续执行上一阶段的编队函数。
3.3 仿真结果与分析
异构集群系统在不同时刻对目标的合围情况如图3所示,其中UAV设定在固定高度20 m飞行,并以颜色区分不同群组。t取0~30 s时,UAV在空中形成圆形编队,并围绕目标旋转,UGV以UAV输出的加权值为中心,在地面形成时变编队,实现对目标的合围;t取30~60 s时,集群系统在控制协议的作用下形成3个子编队,实现对目标的分组围捕。图4表示各架UAV对目标状态的估计值,在t取0~30 s期间,目标运动轨迹相对集中,各架UAV对多目标状态的加权值进行估计,作为编队中心形成期望队形,t取30~60 s期间,目标进行分散机动,各UAV按预定拓扑对分组内的目标状态进行估计,并形成分组队形;由图5可知,各UAV对目标状态估计误差的范数随时间收敛至较小幅值范围内。从图6可以看出,UAV对目标跟踪误差的范数在有限时间内迅速衰减到合理范围内,在t取30 s时集群开始形成分组队形,误差的范数经短暂增大后迅速收敛至较小幅值范围内,说明UAV能够以期望队形跟踪目标输出的凸组合。从图7可以看出,输出合围误差的范数能够收敛至较小范围内,说明UGV的输出能够在控制协议的作用下收敛至UAV输出的凸组合。图8表示UAV对目标状态估计的自适应增益演化曲线。

图3 异构集群系统目标合围示意图Fig.3 Schematic diagram of target containment of heterogeneous swarm system

图4 目标状态估计值Fig.4 Estimation value of target state
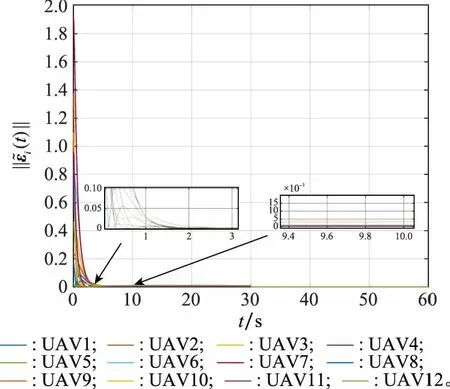
图5 目标状态估计误差Fig.5 Estimation error of target state

图6 UAV目标跟踪误差Fig.6 UAV target tracking error

图7 UGV合围误差Fig.7 UGV containment error

图8 自适应增益Fig.8 Adaptive gain
4 结 论
本文研究了异构集群系统分组编队的跟踪-合围控制问题,主要结论如下:
(1) 系统中目标轨迹通过时变输入进行规划,克服了“自治系统”(无控制输入)机动能力差的缺陷,使后续控制策略的设计过程更符合工程实践;
(2) 为获取目标和领导者状态的凸组合,结合自适应控制理论分别为领导者和跟随者设计基于邻接信息的分布式观测器,实现对时变控制输入的动态补偿,并给出观测器收敛的充分条件;
(3) 针对智能体模型异构的特点,利用状态估计值和输出调节策略,设计分组跟踪-合围控制律,避免了对拉普拉斯矩阵特征值的显式计算,并给出异构无人集群实现分组跟踪-合围的充分条件;
(4) 仿真结果表明,在控制协议的作用下,UAV-UGV异构集群系统能够实现目标的分组合围。
下一步,将对含外部扰动和时延约束的异构集群系统分组编队的合围问题进行深入研究,并对研究成果做进一步验证。
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

