联合最小方差与最大似然谱估计的前视成像方法
祝昇翔, 何 岷, 贺志毅, 王嘉欣
(北京遥感设备研究所, 北京 100854)
0 引 言
雷达成像技术自诞生以来,在军事领域的战场侦察以及民用领域的遥感测绘等方面发挥了重要的作用。与经典的合成孔径雷达(synthetic aperture radar, SAR)成像方式不同的是,前视成像需要对雷达平台的正前方进行成像,其飞行方向与距离向一致,与方位向垂直,无法获得横向的多普勒信息,因此无法通过合成孔径方式来改善方位向的分辨率,这也正是前视成像的难点所在。目前,常用的前视成像方法包括实孔径成像、单脉冲成像、基于反卷积的超分辨成像、双基地前视SAR等[1]。
雷达采用单脉冲测角方式,通过比较多个波束内收到的信号获得目标的角度信息,可用于前视成像[2-6]。文献[2]采用迭代方式,从回波中挑选孤立强点来改善单脉冲鉴角曲线,实现单脉冲图像的方位向自聚焦。文献[3]提出了衡量单脉冲成像性能的3个指标,包括目标图像位置失真、分辨率和图像信噪比。单脉冲成像的问题是受瑞利限的限制,无法实现波束内多目标分辨,只能对图像质量进行非均匀改善[4]。文献[5]采用调频Z变换来重建单脉冲和差通道的多普勒估计,以改善测角精度,但是其性能仍然受制于多普勒梯度差异。文献[6]将贝叶斯自适应直接搜索优化算法用于极化单脉冲前视成像。
反卷积类算法认为,雷达回波在方位向表现为波束与目标角度信息的卷积,并通过反卷积实现超分辨,以获得目标位置信息[7-12]。文献[7]利用泊松和高斯噪声的分布先验信息,采用贝叶斯最大似然准则对反卷积问题进行正则化处理,最后通过迭代求解实现方位向超分辨。文献[8]采用截断奇异值分解法进行反卷积前视成像,在10 dB信噪比仿真条件下,相邻目标的峰谷点差可达6.4 dB。文献[9]提出了基于贝叶斯理论的超分辨方法,以解决最大后验准则下的反卷积问题。文献[10]和文献[11]分别采用了基于全变分的正则化方法和线性预测方法,以改善方位向分辨率。文献[12]构建了多普勒-卷积模型,采用自适应迭代算法重构成像场景。这类算法的问题是在噪声较大时,反卷积问题变为病态问题,难以精确求解,而且算法通常需要迭代计算,难以满足高速运动平台雷达实时成像的要求。
近年来,压缩感知技术、神经网络技术等也被用于前视成像领域[13-17],其性能和实时处理能力也值得关注。文献[13]将压缩感知与稀疏贝叶斯学习算法用于实现超分辨成像。文献[14]基于交替下降条件梯度改善了压缩感知成像存在的网格点失配问题。文献[15]和文献[16]基于随机辐射场的机理和稀疏重构方法提出了微波关联成像算法,并应用于静止平台前视成像。
阵列信号处理理论通过多个传感器在空间的排布实现空域滤波。其中,空间谱估计技术可以增强波束内空间目标的分辨能力,因此也可用于前视成像。Herbert等[18]最早将经典的多重信号分类(multiple signal classification, MUSIC)谱估计用于前视成像,采用天线扫描方式实现了对波束内两个目标的超分辨。多家高校也研究了基于空间谱估计的机载雷达前视超分辨成像[19-22]。
空间谱估计在实际应用时,如果指向角度精度不足,或者场景中存在相干干扰信号,性能会显著下降。文献[23]采用不确定集约束方法对天线阵列的导向矢量进行优化。文献[24]研究了相位量化误差对相控阵天线的影响,并提出了改进方法。文献[25]在传统的空间平滑方法基础上提出了二次平滑方法,以改善阵列的解相干性能。
除了MUSIC谱估计这类子空间算法,最大似然(maximum likelihood,ML)估计是一类基于概率统计思想的算法,适用于低信噪比、小快拍数目和相干信号源条件,性能优于子空间类算法,更加接近于克拉美罗界[26-30]。文献[26]研究了ML估计的分辨概率性能。文献[27]提出了高阶最大似然估计方法。文献[28]将其用于车载雷达的前视目标超分辨,并提出了基于酉变换的方法以简化目标函数求解。文献[29]提出一种两步网格搜索法以减少ML估计的搜索时间,但是该方法有可能错过真正的最大值。文献[30]研究了基于车载雷达平台的ML估计等信号处理算法的高效实现。
高速运动平台相控阵雷达在探测阶段需要对正前方的目标进行检测和跟踪。利用前视成像技术获取二维图像,可以改善目标识别性能,具有重要的应用价值。本文基于阵列信号处理理论,提出一种联合最小方差与ML估计的超分辨前视成像方法,以改善波束宽度内的目标分辨性能。
1 前视成像
1.1 信号模型
设高速运动平台雷达以速度v向正前方飞行,同时波束从左向右扫描。雷达与目标的初始斜距为R0,经过时间ta后斜距为R(ta),其计算方式如下:
(1)
式中:θs为斜视角。
在vta≪R0条件下可近似表示为
(2)
雷达发射线性调频信号,可得到点目标的回波为
(3)
式中:σi为第i个目标的散射系数;tr为距离向快时间;ta为方位向慢时间;rect(·)为矩形脉冲函数;Wa(ta)为方位向的天线方向图函数;fc为载波频率;k为线性调频斜率;c为光速。
对回波进行数字下变频和脉冲压缩后得到
(4)
方位向慢时间对应波束扫描时间:
ta=(θ-θi)/ω
(5)
式中:ω为扫描速度;θi为第i个目标的角度。
因此,以距离和方位角为自变量,所有点目标的回波结果可表示为
(6)

式(6)实际上是一个二维卷积模型,其中距离向由目标散射系数与sinc函数卷积,方位向由目标散射系数与天线方向图卷积。因此,利用天线方向图的辐射空变性和波束扫描的转动时变性,通过天线对雷达正前方的场景进行精准的波束扫描,可以获得距离—方位的二维图像,从而使得雷达获取目标的散射特性信息。
1.2 信号处理架构
雷达系统可以获取不同维度的数据,将其排列在一起即可组成所谓的雷达数据立方体。常用的维度包括距离维、多普勒维、角度维等。常用的三维模型为
e(l,m,n)
(7)
式中:l,m,n分别为距离维、多普勒维和角度维的数据索引;K为目标个数;Ak为信号幅度;λk,μk,νk分别为距离维、多普勒维和角度维的归一化角频率;e为高斯白噪声。
经典的雷达信号处理架构通常先进行距离维和多普勒维的快速傅里叶变换(fast Fourier transform, FFT),在完成目标检测后再对过门限的区域进行角度维的单脉冲测角等处理,此时角度维可获得的快拍数据有限,导致角度分辨率受限。对于前视成像应用,可以先进行角度维处理,然后进行距离维等后续处理。通过波束扫描方式获取不同角度的快拍数据,有利于改善成像效果。此架构可获取距离—方位二维图像,适用于近距离目标高分辨测量,如图1所示。

图1 前视成像架构Fig.1 Architecture of forward-looking imaging
2 超分辨成像
2.1 最小方差谱估计
最小方差谱估计是一种空间谱估计算法,其估计性能优于常规波束形成方法,可改善目标分辨性能。
阵列收到的快拍数据为
X(t)=AS(t)+n(t)
(8)
式中:A=[a(θ1),a(θ2),…,a(θM)]为阵列流形矢量;a(θM)为第M个信源信号的导向矢量;S(t)为信源信号;n(t)为噪声信号。
阵列的协方差矩阵为
(9)
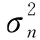
采用最小方差谱估计,按照信号估计无失真且估计方差最小的约束条件,得到最优权值为
(10)
式中:Rx为采样协方差矩阵,是阵列协方差矩阵的估计,由多次快拍取平均计算而得,a(θ0)为目标信号的导向矢量。
按照角度θ进行波束扫描可得到空间功率谱,其峰值对应方向即为信源信号方向:
(11)
2.2 算法修正
最小方差谱估计在真实场景应用中面临多径信号或相干干扰的影响,导致波束指向不精确,使得估计性能下降。
令有用信号为s1(t),相干干扰信号为s2(t)=ρs1(t),阵列接收信号为
y(t)=a(θ1)s1(t)+b(θ2)s2(t)+e(t)=
[a(θ1)+ρb(θ2)]s1(t)+e(t)
(12)
式中:a(θ1)和b(θ2)分别为信号和干扰的导向矢量;e(t)为噪声。
此时信号的导向矢量变为a(θ1)+ρb(θ2),而不再是a(θ1),导致谱估计按照错误的导向矢量进行干扰抑制,使得估计性能下降。
常用的处理相干干扰的算法包括空间平滑算法和矩阵重构算法。其中,空间平滑算法对阵列的各个子阵协方差矩阵求平均,会导致阵列孔径损失,性能下降。而以Toeplitz算法为代表的矩阵重构算法则存在估计方差较大的缺点。本文采用二次平滑[25]加时间平滑的方法进行联合处理。
首先,对采样协方差矩阵进行二次平滑
(13)
然后进行时间平滑
(14)
式中:J为反向单位矩阵,即反对角线元素为1、其他元素为0的矩阵。
采用12 阵元的均匀线阵(uniform linear array, ULA),快拍点数设为256,信噪比为10 dB,设置(0°,5°,10°)的3个信号进行仿真。其中,5°的信号为0°信号的相干干扰信号,相关系数为0.8。标准的最小方差谱估计只能估计出2个峰值,而采用平滑处理修正后则可以估计出3个峰值,如图2所示。

图2 修正前后谱估计结果Fig.2 Spectrum estimation results with and without correction
2.3 ML估计
除了最小方差谱估计,MUSIC谱估计属于另一类基于子空间算法的经典谱估计方法,在理想条件下分辨性能优异。但是在阵列存在误差或相干干扰等非理想条件下,MUSIC谱估计性能显著下降,需要采用空间平滑进行处理,导致阵列孔径损失。最小方差谱估计在采用第2.2节的算法修正后性能有所改善,但是最多只能处理两个相干干扰。另一方面,ML估计通过求解似然函数实现概率统计意义上的最优估计,适用于低信噪比、小快拍数和多个相干干扰等恶劣条件。
在进行空间谱估计时,快拍模型如式(8)所示。通常采用多次快拍进行估计以保证统计性能,其联合概率密度函数为
(15)
式中:det(·)表示矩阵的行列式;σ2为噪声功率;A(θ)为阵列流形矩阵;s(ti)为信号;L为快拍数。
求最大似然估计需要对式(15)取自然对数,再求最大值,从而得到信号和角度的估计值:
(16)

(17)

当信号源个数为1时,式(17)退化为常规波束形成,只能估计出波束内的单个目标。而当信号源个数为K时,则成为一个K维非线性优化问题。直接求解需要遍历搜索空间求极大值,运算量巨大。常用的优化算法有交替投影算法、数学期望最大化算法等,均需要迭代计算,而且无法完全避免只收敛到局部极大值的问题。文献[29]所提方法虽然加快了搜索速度,但也有可能错过全局极大值点。因此,要应用ML估计,一是需要减小搜索空间,二是需要提升单次搜索的计算效率。
采用12阵元ULA阵列,设置角度为(11°,13°)的两个信号,其中13°信号为11°信号的干扰信号,相关系数为0.8。采用ML估计,按照0.01°的搜索网格步长对两个目标进行二维搜索,仿真结果如图3所示。
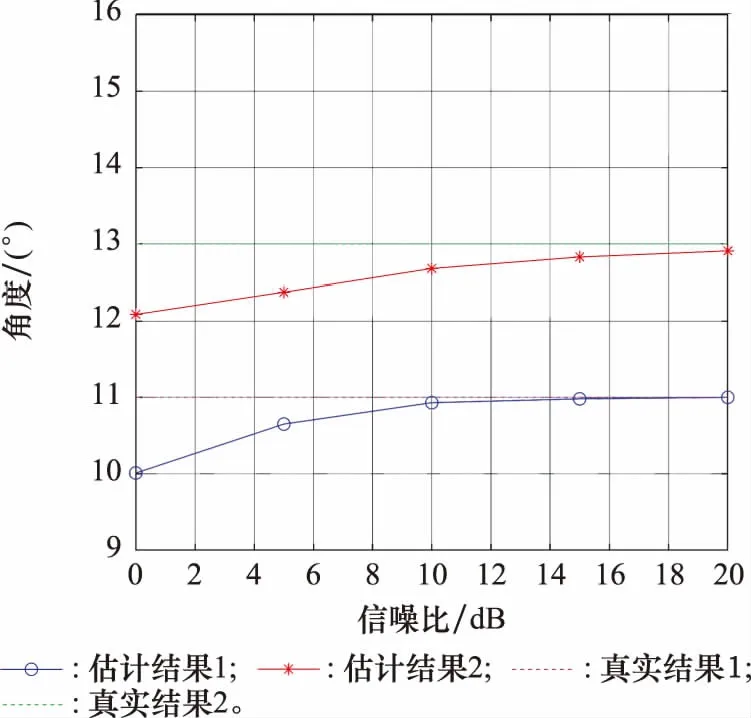
图3 两个相关目标估计结果Fig.3 Estimation results with two correlated targets
由图3可以看出,随着信噪比升高,估计结果收敛到真实值。再设置3个信号,角度为(11°,12°,13°)。其中,12°,13°信号为11°信号的干扰信号,相关系数均为0.4。仍然按照两个目标进行二维搜索,仿真结果如图4所示。

图4 3个相关目标估计结果Fig.4 Estimation results with three correlated targets
由图4可以看出,对于功率相等且相关的两个信号只能估计出一个,但是在大信噪比条件下可收敛到真实值。因此按照两个目标估计,实际有3个信号的场景,仍然可得到两个比较准确的结果,并不会失效。
2.4 超分辨成像算法
用于前视成像的高速运动平台相控阵雷达典型波束宽度为3°~4°,作用距离为1~10 km。由几何关系可知,尽管波束宽度已经很窄,但是波束内同一距离单元的两个目标最大距离可达70~700 m不等,因此波束照射区域内可能存在多个需要分辨的反射点目标。
单脉冲算法可精确估计波束内的单个目标,但无法分辨多个目标。MUSIC谱估计可以实现角度超分辨,但是将其应用于前视成像的缺点是估计结果为伪谱,不能反映目标的真实散射特性,而且必须事先准确估计信源个数,还需要对协方差矩阵进行特征值分解,计算时间较长。最小方差谱估计虽然性能不如前者,但是估计结果为真实功率谱,而且不需要知道信源个数,经过修正处理后性能有所改善,因此可用于前视成像的粗估计。在粗估计的基础上,可采用ML估计进行小范围搜索,进一步改善目标分辨性能。因此,提出一种联合最小方差与ML估计的前视成像方法,如图5所示。步骤如下:

图5 超分辨前视成像算法步骤Fig.5 Procedures of super-resolution forward-looking imaging algorithm
(1) 对雷达平台正前方进行波束扫描并录取回波。采用最小方差谱估计计算最优权值,实现波束形成,见第2.1节;
(2) 在谱估计计算过程中进行修正处理,见第2.2节;
(3) 对每个脉冲重复周期波束形成的结果进行脉冲压缩;
(4) 对每个角度驻留的n个脉冲进行非相参积累,只保留一组结果,得到距离—方位二维图像;
(5) 对图像进行目标检测,找到幅度峰值过门限的区域,再根据典型目标的尺寸限定目标所在区域大小;
(6) 使用目标所在距离门的方位向数据计算得到协方差矩阵。然后,以各目标所在区域的峰值点为中心,分别进行ML估计的搜索;
(7) 将目标估计结果上报或进行其他后处理。
3 仿真校验
采用16阵元的ULA阵列,方位向3 dB波束宽度约为6.3°,发射线性调频波形。雷达平台高度为1 000 m,x方向速度为100 m/s。设置3个点目标,其雷达散射截面积(radar cross section, RCS)均为1 m2,坐标分别为(4 500,-40),(4 500,0),(4 500,40),目标角度间隔为0.51°。设置参数如表1所示。波束扫描角度步长设为0.1°,信噪比为25 dB。首先,采用最小方差谱估计进行前视成像仿真。可以看出,在较高信噪比条件下可以实现波束内3个不相关目标的分辨,如图6所示。

表1 仿真参数Table 1 Simulation parameters

图6 3个不相关目标成像结果Fig.6 Imaging result of three uncorrelated targets
将目标2和目标3改为目标1的相关信号,相关系数均为0.3,再进行仿真。此时,最小方差谱估计的成像结果只有一个尖峰,无法分辨出3个目标,如图7所示。因此,最小方差谱估计的成像结果无法分辨相关信号,只能作为粗估计结果。

图7 3个相关目标成像结果Fig.7 Imaging result of three correlated targets
在粗估计的基础上对图像进行目标检测,然后根据目标所在区域,在方位向进行ML估计搜索和计算。设置搜索网格步长为0.05°,估计结果如图8所示。图8中,黑色虚线为目标真实位置,蓝色实线为由最小方差谱估计得到的粗估计结果,红色实线为ML估计结果。从仿真结果可以看出,在3个相关目标的条件下用二维ML估计可以估计出其中两个目标。

图8 方位向成像结果Fig.8 Azimuth imaging result
为了进一步评估本方法的性能,将ML估计与谱估计类成像方法中的MUSIC谱估计[18,20-22]进行对比。在不同信噪比和目标角度间隔条件下,采用这两种方法分别对相关目标和不相关目标进行了100次蒙特卡罗仿真,仿真结果如图9和图10所示。由于标准MUSIC算法在相关信号条件下性能显著下降,因此这里对其进行了前向-后向空间平滑处理。可以看出,ML估计在低信噪比和目标角度间隔相对较小的条件下估计性能更好,在相关信号条件下性能虽然有所下降,但是仍明显优于使用空间平滑的MUSIC谱估计。此外,对ML估计的搜索步长的不同取值进行仿真,仿真结果如图11所示。

图9 不同信噪比估计结果Fig.9 Estimation results with different signal-to-noise ratios

图10 不同角度间隔估计结果Fig.10 Estimation results with different azimuth intervals

图11 不同步长估计结果Fig.11 Estimation results with different steps
由图11可以看出,在不相关目标条件下,搜索步长越小则估计误差越小,而在相关目标条件下,减小搜索步长对估计误差改善不明显。由于搜索步长的大小直接影响成像的实时性,综合考虑估计性能和实时性要求,可以选择搜索步长小于等于扫描步长的一半。
为了评估本方法的计算量,对ML估计与MUSIC谱估计分别按照2个目标和3个目标进行估计,算法复杂度比较如表2所示。其中,N为天线通道数,M为谱估计的一维搜索次数。可以看出,ML估计需要多维搜索,因此搜索次数远大于MUSIC谱估计。但是,单次计算所需的乘法和加法次数较少,而且不需要复杂的矩阵特征值分解和信源个数估计运算。因此, 在目标数较小的条件下可以实现实时处理。本文方法通过最小方差谱估计的粗估计结果确定搜索区域,可以缩小搜索范围,从而减小搜索次数,达到改善成像实时性的目的。

表2 算法复杂度比较Table 2 Algorithm complexity comparison
4 结 论
针对传统前视成像算法存在的方位向分辨率不足的问题,本文基于阵列信号处理理论提出了一种联合最小方差与ML估计的超分辨前视成像方法,通过修正和联合处理,突破了瑞利限的限制,改善了波束内多个目标的分辨性能。
仿真实例说明了该方法的有效性,在波束内存在多个目标的场景下可估计出波束内至少两个目标的信息,具有一定的工程应用价值。虽然理论上可以支持全部分辨3个甚至更多目标的场景,但是全局搜索计算复杂度过高,无法满足目前高速运动平台的实时处理要求,而目前的快速ML估计优化算法如交替投影算法、数学期望最大化算法等也存在一定局限,后续还需要进一步探索算法实时性提升手段,并保证求解的稳定性。

