Searching for a0(980)-meson parton distribution function

Zai-Hui Wu, Hai-Bing Fu, Tao Zhong, Yu Chen and Ya-Hong Dai

Department of Physics, Guizhou Minzu University, Guiyang 550025, China

Abstract In this paper, we calculate the scalar a0(980)-meson leading-twist wave function by using the light-cone harmonic oscillator model (LCHO), where the model parameters are determined by fitting the ξ-momentsof its light-cone distribution amplitudes.Then, the a0(980)-meson leading-twist light-cone distribution amplitudes with three different scales ζ=(1.0, 2.0, 5.2)GeV are given.After constructing the relationship between the a0(980)-meson leading-twist parton distribution functions/valence quark distribution function and its LCHO wave function,we exhibit theq a0(x,ζ)andxq a0(x,ζ)with different scales.Furthermore, we also calculate the Mellin moments of the a0(980)-meson’s valence quark distribution function〈x n qa0 〉ζwith n=(1,2,3),i.e.〈xqa0〉ζ 5=0.027,〈x 2qa0〉ζ 5=0.018and〈x 3qa0〉ζ 5=0.013.Finally, the scale evolution for the ratio of the Mellin momentsxna0(ζ ,ζk)are presented.

Keywords: parton distribution functions, light-cone distribution amplitudes, light scalar meson,light-cone harmonic oscillator model

1.Introduction

The exploration of quark-gluon structure hadrons has been a cutting-edge issue across particle physics and medium-high energy nuclear physics in recent years.Among them, quarks and gluons, called partons, are the fundamental degrees of freedom of quantum chromodynamics (QCD).Although the parton can not be directly observed, the QCD factorization theorem allows one to express the information of the parton inside the nucleon in terms of nonperturbative functions [1].At the same time, the parton distribution function (PDF) is considered to be the most important nonperturbative function,which plays an important role in describing the nonperturbative QCD for the internal structure of hadronic bound states [2].In addition, it also gives the probability of finding quarks and gluons inside a hadron.In the infinite momentum coordinate system [3-6], PDFs are used to describe the onedimensional momentum distributions of quarks and gluons.Therefore, the internal structure of hadrons can be studied by calculating the meson’s PDF.

The PDF constitutes the basic limit of the Higgs boson characterization in the matter of coupling and is the main system for Standard Model (SM) measurements such asWboson mass.Also,it is still the largest uncertainty outside the production of SM heavy particles so it has important phenomenological value.The MMHT[7], CT [8], NNPDF [9],HERAPDF[10],and JAM[11]have made substantial efforts to determine PDFs and their uncertainties.The pion deemed to the lightest bound state of QCD and kaon has been predicted by many theoretical calculations, chiral-quark model[12-14], Nambu-Jona-Lasinio model [15], light-front holographic QCD (LHFQCD) [16-19], light front quantization[20-22], maximum entropy method [23, 24], Dyson-Schwinger equations (DSEs) [25-35] and lattice QCD[36-45]for the valence quark PDF.Meanwhile,PDFs can be attained directly from the light-front wave function (LFWF),which has been researched via the Bethe-Salpeter wave functions within covariant DSEs, LHFCD and BLFQ.The scalar mesons below 1 GeV are an interesting field to researchers, especially fora0(980) state.Its internal structure has some pictures, such as quark-antiquark states[46-51],tetraquark states [52-57], two-meson molecule-bound states[58-62] and hybrid states [63].In this paper, we mainly take thea0(980) state as the quark-antiquark picture.Until now,there is less research about the scalar mesona0(980) PDFs.Thus, in order to understand the internal structure of thea0(980)-meson, thea0(980)-meson parton distribution function will be studied in this paper.

One of the earliest predictions for theJ=0 meson valence-quark distribution function for large-xbehaviour within the QCD improved parton model [64-66], has the following expression:

wherec(ζ) is independent ofxand the ζ stands for the resolving scale.The symbol‘M’stands for eachJ=0 meson.Since the meson’s PDF can be obtained directly from its wave function (WF), a more accuratea0(980)-meson WF is crucial for us to determine its PDF.The light-cone harmonic oscillator model (LCHO) for the light or heavy meson WF is mainly based on the Brodsky-Huang-Lepage (BHL) prescription [67], which has been used in many cases [68-76].For this model,the total WF can be separated into spin-space WF(x,k⊥)and spatial wave functionψRM(x,k⊥).The spatial WF is divided into thex-dependence part and the k⊥-dependence part for calculation.The k⊥-dependence part derives from the approximate bound-state solution and thexdependence part φM(x) can be expanded in Gegenbauer polynomials.

Furthermore, the meson light-cone distribution amplitudes (LCDAs) can also be related to its WF, which leads to the indirect relationship between meson LCDAs and PDFs.In many applications of LCDAs, one usually takes a truncated form to determine DAs, involving only the first few terms of the Gegenbauer expansion series.With the increase ofn,there will exist dimensional anomalies which lead to spurious oscillations.In addition, one of the most important factors is the unreliability of the higher-order Gegenbauer moments.In order to improve this phenomenon,one can adopt the LCHO model to deal with the meson LCDAs.In our previous works[76,77],meson leading-twist LCDAs are studied by using the LCHO model, and then the model parameters are determined by fitting moments with the least squares method.Therefore,we will study thea0(980)-meson PDFs based on BHL prescription in this paper.

2.Theoretical framework

If one wants to use the typical probability expression of quantum mechanics to describe the measurable properties of a given hadron, the first thing one needs to do is find the WF.Each element of the WF Fock-space decomposition represents the probability amplitude of findingncomponents in the hadron.However, the PDFs describe the longitudinal momentum distribution parton of the hadron.To derive thea0(980)-meson leading-twist PDF, the following expression can be used [34]

whereψa0(x,k⊥)is WF and ζ stands for the scale.In order to calculate the PDF, the connection between distribution amplitudes and distribution function can be established to achieve the purpose.Exploiting this relationship, one can predicta0(980)-meson leading-twist PDFs with the LCHO model based on the BHL description[67,75,78].The LCHO model of thea0(980)-meson leading-twist WF is denoted by

where k⊥is transverse momentum and the symbol‘R’means that(x,k⊥)is the spatial wave function in coordinate form.The LCHO model consists of the spin wave function(x,k⊥)and(x,k⊥)as the space wave function.Furthermore, λ1and λ2are the helicities of the two constituent quarks.The spin-space WF(x,k⊥)comes from the Wigner-Melosh rotation.The different forms for λ1λ2can also be found in[75].Thus the sum of the spin-space WF has the following form

withmq=mu=md.On the other hand, the BHL description proposed the assumption that the valence Fock WF depends only on the energy variable ∊outside the shell.At the same time, the connection between the equal-time WF in the rest frame and the light-cone wave function in the infinite frame by equating the energy propagator∊=M2- (ki)2is proposed.The propagators in different frames are as follows

where the indexiis represented as the parton,wheni=1,it is represented as theu-quark, andi=2 is represented as thedquark.For the two-particle system, one can get

whereq10=q20.Besides,the rest frame wave function ψCM(q)and the light-cone wave function ψLC(x,k)might be related in some way [75]

In this paper, based on the approximation for the bound state solution of the meson quark model, the WF of the harmonic oscillator model in the rest frame is expressed as

Combining equations (7) and(8), the spatial WF fora0(980)-meson can be obtained

where the free parametersAa0stands for normalization constant, the harmonious parameterβa0can determine the transverse distribution amplitudes of meson WF andφa(x)is0crucial for determining the WF longitudinal distribution amplitude.It can be expressed in terms of the first few terms of the Gegenbauer moment polynomials since thea0(980)-meson leading-twist amplitude is antisymmetric underu→(1-u) transition in theSUf(3) limit.

By using the relation between thea0(980)-meson wavefunction and its distribution amplitude,

And by combining(4) with(10), one can get thea0(980)-meson leading-twist WF

We find that thein equation (18) has a certain influence on adjusting the LCDA’s behavior, soxcan be introduced into the longitudinal distribution amplitude, the expression is as follows,

where the free parameterαa0can be obtained by fitting moment 〈〉ζwith the least square method.Furthermore,thea0(980)-meson leading-twist valence-quark distribution function can be obtained by integrating over the squared transverse momentum, i.e.Equation (2), which leads to the following formula

Then, the ratio of Mellin moments is also a point of interest,and its expression is as follows

Another significant physical quantity associated with thea0(980)-meson PDF is its LCDA.The relationship between thea0(980)-meson leading-twist LCDA and the WF is

After integrating over the squared transverse momentum,one can get the LCDA formula

On the other hand, the ξ-moments can be calculated by the QCD sum rule approach within background field theory(BFTSR).The two-point correlation function is taken as

withntaking the odd numbers, while the even order will vanish due to theG-parity.The currents areThe detailed calculation process for the ξ-moments is given in our recent paper [79].

Then, one can adopt the least squares method to fit ξmoments 〈〉ζin determining the free model parameters.The purpose of the least squares method is to obtain the optimal value of the fitting parameter θ by minimizing the likelihood function

where μ(xi, θ) is thea0(980)-meson ξ-moments 〈〉ζof combining equations(18)and(19).The value ofyiand its variance σiare defined as the value of ξ-moments calculated by the QCD sum rule.Beyond that, making use of the probability density functionof χ2, one can get the goodness of fit with the following probabilityPχ2

with∈(0, 1).The closer the goodness of fit is to 1, the better the parameters are obtained.Incorporating the effect of scale ζ, according to the renormalization group equations of Gegenbauer moments of thea0(980)-meson leading-twist LCDA,

withCF=4/3.Then, one can gain the ξ-moments at the arbitrary scales ζ.Then,by fitting moments 〈ξna0〉ζunder the different scale ζ with the least square method, LCDA i.e, equation (18)under corresponding scales can be obtained.Finally, according to the wave functions under different scales,we can calculate thea0(980)-meson valence quark distribution function, Mellin moments〈xnqa0〉ζand ratioxna0(ζ,ζk)with different scales by using equations (2), (15) and (16).

3.Numerical analysis

To do the numerical analysis, the following input parameters are used.The mass ofa0(980)-meson is taken asma0=0.980 ±0.020 GeV.The current light quark-mass,charm quark mass,the values of the non-perturbative vacuum condensates, the continuum thresholds0and the corresponding Borel windows used in ξ-moments BFTSR are consistent with our previous work[79].Generally,we can treat it as the constituent quarkmqfor thea0(980)-meson with the quark componentqq.In this paper, we take three typical scales, the initial scales ζ0=1.0 GeV, the processes scale ζ2=2.0 GeV and the scale for π-nucleon Drell-Yan experiment[80]or the E615 experiment ζ5=5.2 GeV,which agree with the pion cases [34].

Firstly,based on the sum rule for distribution amplitudes moments 〈〉ζcalculated in our previous work [79], we list thea0(980)-meson leading-twist LCDA ξ-moments 〈〉ζwith three different scales ζ=(1.0, 2.0, 5.2)GeV in table 1.Here,the accuracy of our calculation is up to the 9th order.It can be seen that the absolute value of ξ-moments decreases as the scale ζ increases.Secondly, the absolute value of ξmoments decreases as thenincreases, which shows that our calculation has good convergence.Then, we adopt the least squares method to fit the ξ-moments 〈〉ζ.At the same time,thea0(980)-meson twist-2 distribution amplitudes withdifferent constituent quarksmq=(200, 250, 300, 350)MeV are shown in figure 1.The result shows that constituent quarksmqhave a certain influence on distribution amplitudes.It is taken to be 250 MeV in the invariant meson mass scheme[81-87] or 330 MeV in the spin-averaged meson mass[89-93].In this paper, we mainly takemq=250 MeV.Then,the fitting model parameters with the different scale ζ are given in table 2.Based on the experience of other mesons[69-72,76,77,88,94,95],we take the WF model parameterβa0= 0.5.Obviously,Aa0gradually decreases with the increment of the scale ζ.However,the goodness of fitis not very well when the scale is higher, such as ζ=5.2 GeV.The reason may lie in the higher-order Gegenbauer moments taking a higher contribution with a larger scale.

Table 1.The a0(980)-meson leading-twist LCDA moments 〈 〉ζat scales ζ=(1.0, 2.0, 5.2) GeV.

Table 1.The a0(980)-meson leading-twist LCDA moments 〈 〉ζat scales ζ=(1.0, 2.0, 5.2) GeV.

ζ0ζ2ζ5 ξ 1〈 〉ζ 0-0.309±0.043 -0.214±0.029 -0.159±0.022 ξ a 3〈 〉ζ 0-0.184±0.032 -0.093±0.016 -0.049±0.009 ξ a 5〈 〉ζ 0-0.082±0.027 -0.057±0.017 -0.040±0.011 ξ a 7〈 〉ζ 0-0.053±0.025 -0.037±0.015 -0.026±0.010 ξ a 9〈 〉ζ a 0-0.043±0.034 -0.014±0.0110.001±0.005

Table 2.The LCHO model parameters Aa0 (in unit: GeV-1),βa0 (in unit: GeV),αa0 and goodness of fitchanged with the factorization scales ζ=(1.0, 2.0, 5.2) GeV.

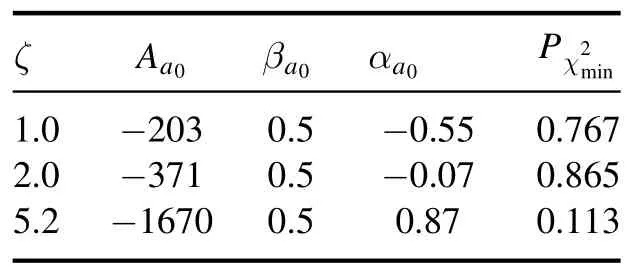
Table 2.The LCHO model parameters Aa0 (in unit: GeV-1),βa0 (in unit: GeV),αa0 and goodness of fitchanged with the factorization scales ζ=(1.0, 2.0, 5.2) GeV.

ζAa0βa0αa0Pχmin 2 1.0-2030.5-0.550.767 2.0-3710.5-0.070.865 5.2 -1670 0.50.870.113

With the resultant LCHO model parameters, the curves ofa0(980)-meson leading-twist LCDA with three scales ζ are shown in figure 2.The figure shows that

· The behavior of the three curves tends to be antisymmetric,which will equal zero when the LCDA integrates with respect tox, e.g.

Meanwhile, the three curves go through the zero at the locationx=0.5.

· The absolute value of the peaks is decreased with the increase of ζ and thex-location of the peaks tends toward 0.5 with the ζ increase.When the scale tends to infinity i.e.ζ →∞,the curve ofa0(980)-meson LCDA will tend to asymptotic formφa0(x,∞)=0.

Secondly, after taking the LCHO parameters into thea0(980)-meson valence-quark distribution function, e.g.Equation (14), the predictions ofqa0(x,ζ)can be obtained.

Figure 1.The a0(980)-meson LCDA with different quark masses mq=(200, 250, 300, 350)MeV.

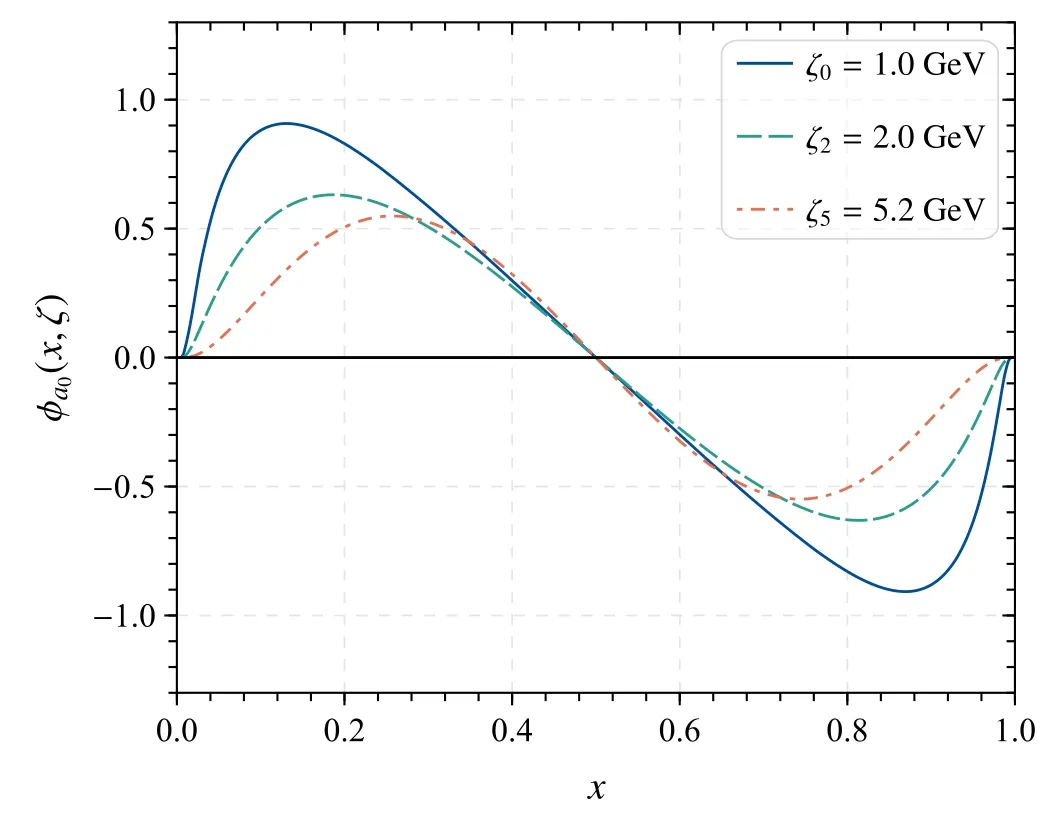
Figure 2.The a0(980)-meson leading-twist LCDAφa0(x,ζ)changed with three different scales ζ=(1.0, 2.0, 5.2) GeV.

The curves ofa0(980)-meson valence-quark distribution functionwith different scales ζ are shown in figure 3, which shows that the value of peaks decreases with the increase of scale ζ.Since thea0(980)-meson leading-twist LCDA is antisymmetric behavior under theu→(1-u)interchange in the SUf(3)limit,its valence-quark distribution functionxqa0(x,ζ)tends to zero atx=0.5.Additionally,the valence-quark distribution function tends toward bimodal behavior.In general,the valence-quark distribution functions of pion and kaon tend to a unimodal behavior [34].

Using the meson’s valence quark distribution function,we can get the Mellin moments〈xnqa0〉ζof thea0(980)-meson valence-quark distribution function, which are presented in table 3.From the table, we can see that the Mellin moments convergence with the ordernincreased.Meanwhile, the Mellin moments’convergence with the scale ζ increased.This agrees with the Mellin moments of pion’s valence-quark distribution function decreasing with the increase of scale.The greater ζ,the smaller the value of the moments in[34].It proves our prediction of the Mellin moments〈xnqa0〉ζis reasonable.

Figure 3.The a0(980)-meson valence quark distribution function q a0(x,ζ)andxq a0(x,ζ)with different scales.

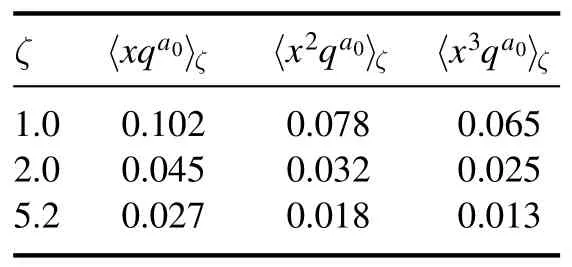
Table 3.The Mellin moments for a0(980)-meson leading-twist distribution function〈x n qa0 〉ζwith different scales ζ=(1.0, 2.0,5.2) GeV.

Finally, we also calculate the ratioxna0(ζ,ζk)of Mellin moments changed with the scale ζ.The predictions of the ratio of Mellin moments with three fixed scales ζk=(1.0,2.0,5.2)GeV and different ordersn=(1, 2, 3) are depicted in figure 4.It is obvious that thexna0(ζ,ζk)are increased with indexnbefore the point of ζk, and decreased withnafter ζk.The curves ofxna0(ζ,ζk)are decreasing as the ζ increases.The curves will coincide with each other when the scale ζ and ζktend to infinity.

4.Summary

In this paper, we fit moments〈xan0〉ζwith the least squares method to obtain the free model parametersAa0,βa0andαa0at the scales ζ=(1.0,2.0,5.2)GeV.Meanwhile,the goodness of fitis also given.Then, we present the curves ofa0(980)-meson leading-twist LCDA shown in figure 2.After constructing the relationship betweena0(980)-meson leadingtwist WF and PDFs, thea0(980)-meson valence quark distribution functionqa0(x,ζ)andxqa0(x,ζ)with different scales are shown in figure 3,which tends to bimodal behavior.The LCDA and PDFs tend to zero at the locationx=0.5 due to the antisymmetry of the WF.Based on thea0(980)-meson valence quark distribution function, we can get the first three order Mellin moments〈xqa0〉ζof thea0(980)-meson valence quark DF shown in table 3.Referring to the predicted pion’s Mellin moments, our predicted result is quite reasonable.At the same time, we also give the ratioxna0(ζ,ζk)of Mellin moments with ζ=(1.0,2.0,5.2)GeV shown in figure 4.The ratioxna0(ζ,ζk)shows a downward tendency with the increase of ζ.

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China under Grant No.12265010,No.12265009, the Project of Guizhou Provincial Department of Science and Technology under Grant No.ZK[2021]024,the Project of Guizhou Provincial Department of Education under Grant No.KY[2021]030.

ORCID iDs