Multiple soliton solutions and symmetry analysis of a nonlocal coupled KP system

Xi-zhong Liu, Jie-tong Li and Jun Yu

Institute of Nonlinear Science, Shaoxing University, Shaoxing 312000, China

Abstract A nonlocal coupled Kadomtsev-Petviashivili(ncKP)system with shifted parity( )and delayed time reversal () symmetries is generated from the local coupled Kadomtsev-Petviashivili(cKP)system.By introducing new dependent variables which have determined parities under the action of, the ncKP is transformed to a local system.Through this way, multiple even number of soliton solutions of the ncKPI system are generated from N-soliton solutions of the cKP system, which become breathers by choosing appropriate parameters.The standard Lie symmetry method is also applied on the ncKPII system to get its symmetry reduction solutions.

Keywords: nonlocal coupled Kadomtsev-Petviashivili system, N-soliton solutions, symmetry reduction solutions

1.Introduction

In 2013 Ablowitz and Musslimani introduced a new nonlocal nonlinear Schrödinger (nNLS) equation [1]

withq*(−x,t) being complex conjugate ofq(−x,t), which is proved to be integrable under the meaning that it has a Lax pair and an infinite number of conservation laws.Contrary to local equations where dependent variables have the same independent variables, dependent variables of a nonlocal equation have two or more independent variables which are usually linked by space and/or time reversion, such as the variables of (−x,t) and (x,t) in equation (1).Since the work of [1], nonlocal versions of many famous nonlinear systems,such as the Korteweg de-Vries (KdV) and modified KdV equation, the sine-Gordon equation, the Kadomtsev-Petviashivili (KP) equation, Sasa-Satsuma equation, etc are introduced and studied by applying various methods including inverse scattering transform [2, 3], Riemann-Hilbert method[4, 5], the Hirota’s bilinear method [6-9], the Darboux transformations [10-12], Wronskian technique [13],symmetry analysis [14], deep learning neural network framework [15] and so on.

In recent years, Lou and Huang proposed the concept of the Alice-Bob(AB)system to describe two correlated events which can be assumed to be related by an operator, e.g.A=, wherecan be taken as shifted parity and delayed time reversal and so forth [16].In other words, there exist at least two spacetime coordinates in one AB system.In this context, many AB-type nonlocal systems are constructed including the AB-KdV equation [17], AB-mKdV equation[18], AB-AKNS system [17], etc.In [19], a consistent correlated bang (CCB) method is proposed from which one can generate nonlocal systems from known local ones [20, 21].

The coupled KP (cKP) system [22-25] takes the form

which was first appeared in a paper of Jimbo and Miwa in Hirota bilinear form [26], it has N-soliton solutions expressed in terms of Pfaffians [27].The cKP system (2) can be categorized as cKPI by taking σ2=−1 and cKPII by taking σ2=1.In [23, 28], a host of solitonic interactions of the cKP are obtained, among which peculiar spider-web solutions are obtained and analyzed.In this paper, inspired by the CCB method,we introduce a nonlocal coupled KP(ncKP)system as

with

and probe its exact solutions and symmetry properties.

The paper is organized as follows.In section 2, we convert the ncKPI (σ2=−1) system into a local system by introducing some new variables with definite parity properties to replace the variables of the ncKPI system.Then we use N-soliton solutions of the cKP system to generate an even number of N-soliton solutions of the ncKPI system.In section 3,we apply the standard Lie symmetry method on the ncKPII (σ2=1) system to give its Lie symmetry group and similarity reduction solutions.The last section is devoted to a summary.

2.Multiple soliton solutions of the ncKPI system

To convert the ncKPI system into a local system,considering the relation (9), we take

with

Substituting equation (10) into the ncKP system (3)-(9) we split it into the following equations

It can be seen that equations (12)-(14) are just the cKPI system (2) with σ2=−1 while equations (15)-(17) are linearized equations of the cKPI system.

The cKP system(2)has the following N-soliton solution[22]

with α being a nonzero real number, which is an extension of N-soliton solutions of the KP equation, the summations should be done for all permutations ofνi＇=0, 1(i＇ =1, 2, 3,…N), and

with arbitrary constantskj,rj, ξj0, (j=1, 2, 3, …,N).

Considering thatu,vandwin equation(18)are invariant under the following transformation

we rewrite

where

with arbitrary constantsy0jand η0j.So the N-soliton solutions of the cKPI system can be rewritten as [17]

where the summation of ν being done for all non-dual permutations ofνi＇= 1, -1,(i＇ =1, 2, 3,…N)and

It is clear that solutions ofu1,v1, andw1in equations(15)-(17)are symmetries of the cKP system,which can be taken as

wheref1,f2andf3are arbitrary functions oftsatisfying

It can be verified that equation (21) with equation (22)satisfies the condition of equation (11).So, N-soliton solutions of the ncKPI system (12)-(14) can be expressed by equation (10) with equations (19) and (21).

By the condition of equation(20),odd number solitons of the ncKPI system are prohibited.As forN=2,4,the explicit expressions ofFNin equation (19) are

and

where

and

At timet=0, forN=2 case, figures 1(a) and 2(a) give density plot and three-dimensional plot ofAof the ncKP system expressed by equations (10) with equations (19) and(21) where the parameters are fixed by

as forN=4 case, figures 1(b) and 2(b) give density plot and three-dimensional plot ofAof the ncKPI system where the parameters are fixed by

BecauseF2(orF4) in equations (23) (or (24)) depends similarly on the coordinates ofx,yandt,the multiple soliton interaction behaviors ofAdepending on other variable pairs(x,t) and (y,t) are similar to those in figures 1 and 2.

Whenrj(j=1, 2, 3, …,N) in equation (19) are taken to be a pure imaginary number, these N-soliton solutions become breather solutions.To illustrate this point, for theN=2 case, when we take the parameters as

we get breathers at timet=0 in figure 3.

It is well known that the KP equation has lump solutions,we can verify that the cKPI system has the following solution

with arbitrary constantsd,x0,y0,t0,which leads to lump-type solutions of the ncKP system by substituting equation (28)into equations(10)with equation(21).Figure 4 demonstrates a lump-type solution of the ncKPI system for the variableA,where the parameters are fixed by

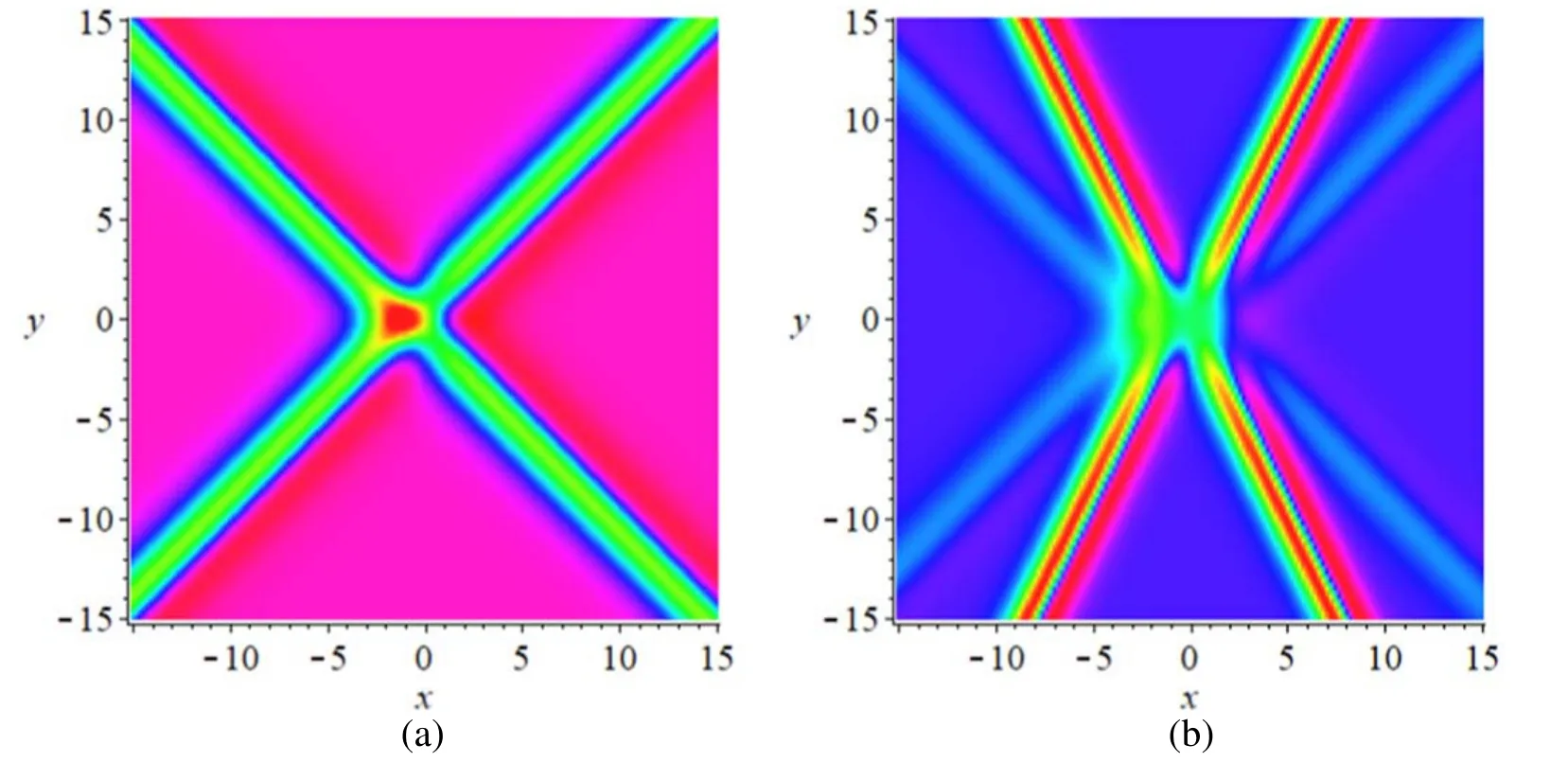
Figure 1.(a)The density plot of the solution A of the ncKPI system at time t=0 for N=2 case with parameters being fixed by equation(25);(b) the density plot of the solution A of the ncKPI system at time t=0 for N=4 case with parameters being fixed by equation (26).

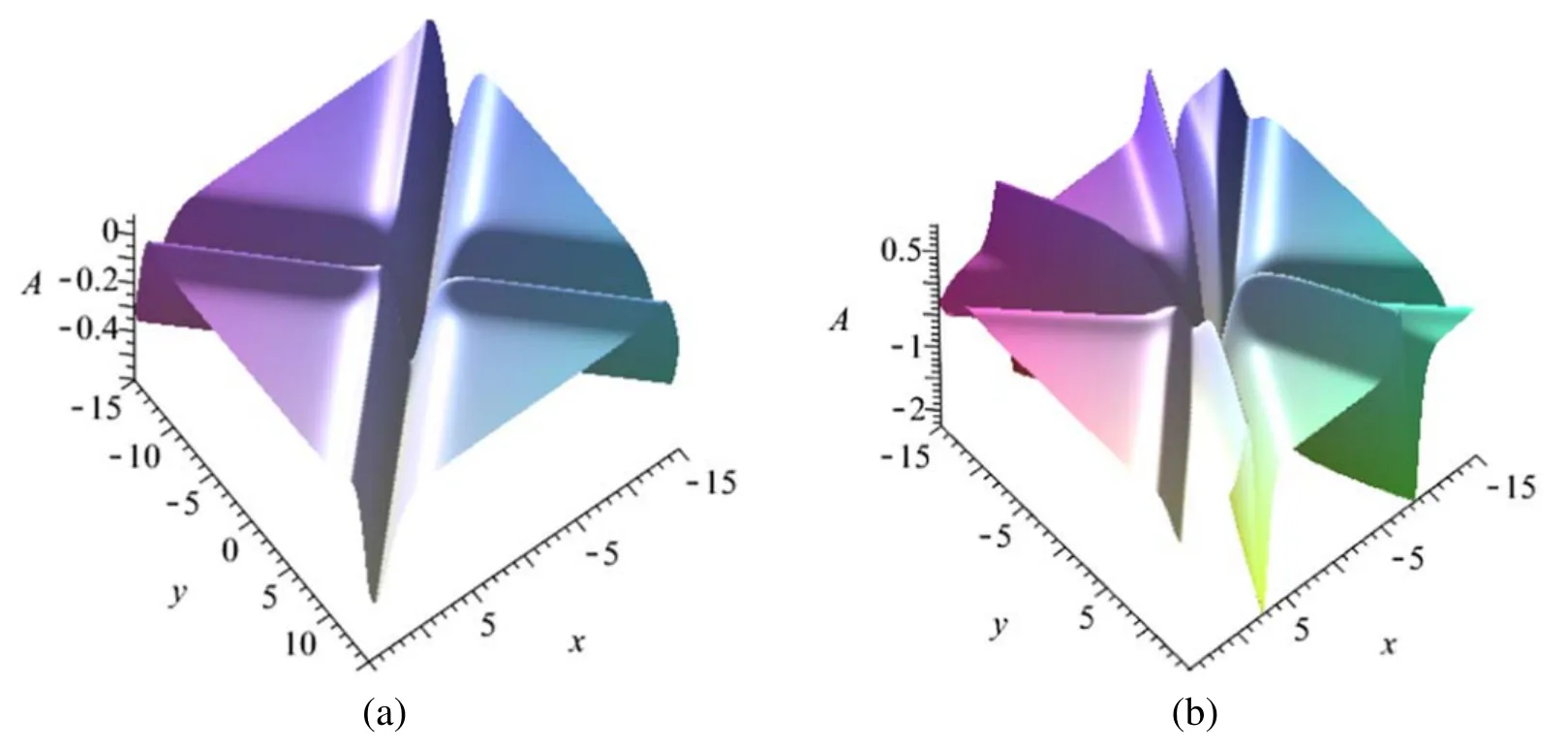
Figure 2.(a) The three-dimensional plot of the solution A of the ncKPI system at time t=0 for N=2 case with parameters being fixed by equation(25);(b)the three-dimensional plot of the solution A of the ncKPI system at time t=0 for N=4 case with parameters being fixed by equation (26).

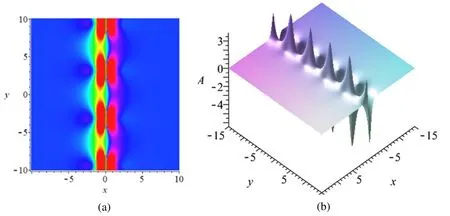
Figure 3.Breather solutions of the ncKPI system at time t=0 for:(a)the density plots of the variable A;(b)the three-dimensional plots of the variable A.The parameters are fixed by equation (27).

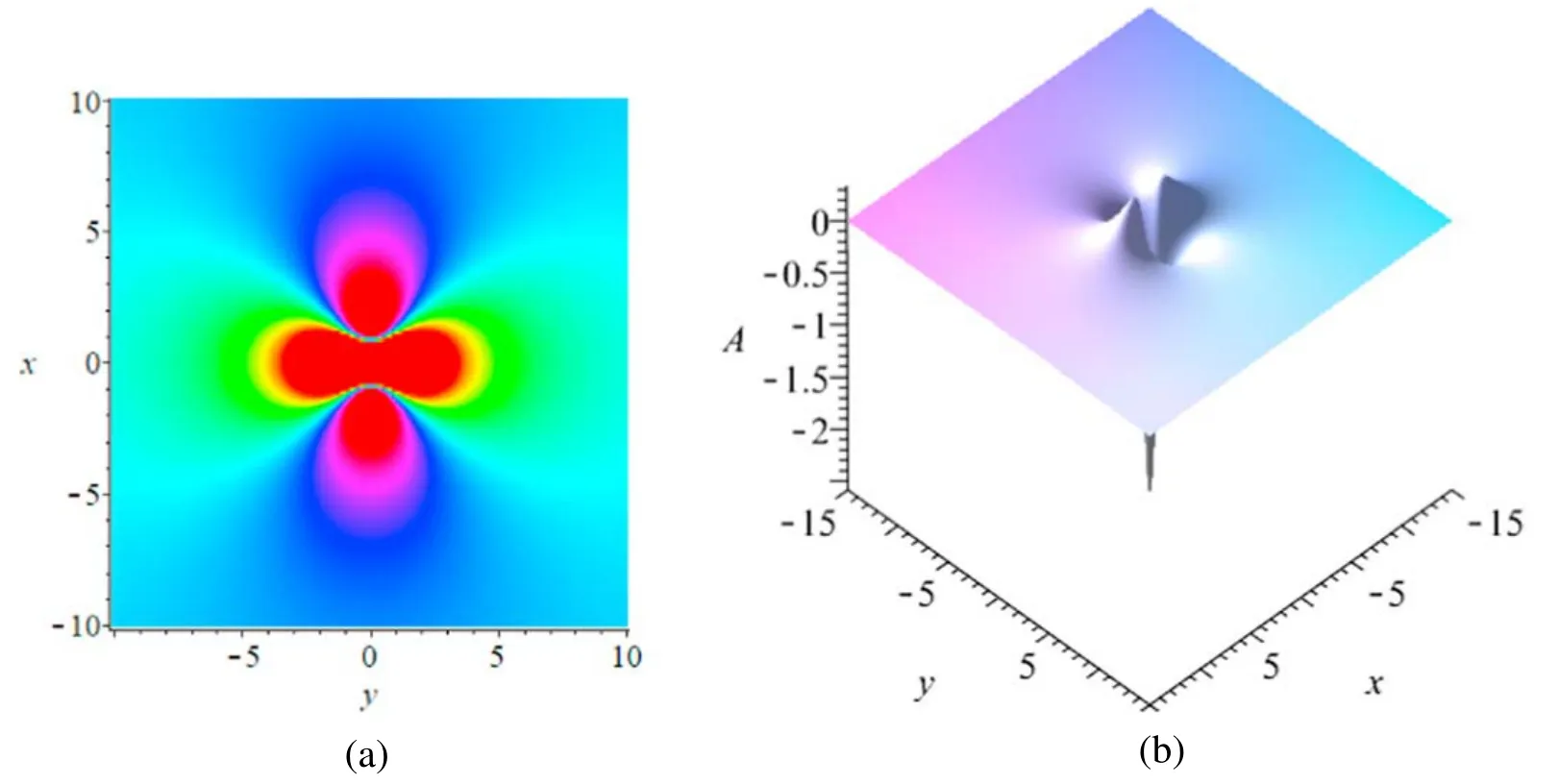
Figure 4.Plots of lump solution of A of the ncKPI system at time t=0,while the parameters being fixed by equation(29):(a)density plot;(b) three-dimensional plot.

3.Symmetry reduction solutions of the the ncKPII system

Symmetry analysis plays an important role in solving nonlinear systems [29, 30], in this section we apply the standard Lie symmetry method on the ncKPII system.To this end,we first give the Lie point symmetry of this system in the form

whereX,Y,T,Γ1,Γ2,Γ3,Λ1,Λ2,Λ3are functions ofx,y,t,A,B,C,E,F,Gthat needs to be determined.In other words,the ncKPII system is invariant under the following transformation

with infinitesimal parameter ∊.The symmetry of equation(30)can be written in function form as

which satisfy the linearized equations of the ncKPII system

and also the nonlocal condition

By substituting equations (31) into equation (32) and eliminatingAxt,Bxt,Cxt,Ext,Fxt,Gxtby the ncKPII system,we obtain a system of the functionsX,Y,T,Γ1,Γ2,Γ3,Λ1,Λ2,Λ3.By vanishing all independent partial derivatives of variablesA,B,C,E,F,Gwe obtain a system of over determined linear equations, which can be solved by software likemaple.After considering the nonlocal relation of equation (32g), we have

wheref1,f2,f3are arbitrary functions oftsatisfying the condition of (22).So the explicit expressions of equation (31)are

Group invariant solutions of the ncKPII system can be obtained by solving equation (33) under the condition σA=σB=σC=σE=σF=σG=0, which is equivalent to solving the characteristic equation

After solving equation (34) we get symmetry reduction solutions of the ncKPII system

whereA1,B1,C1,E1,F1,G1are invariant functions of two new invariant variables

In equation(41),m1,m2,m3are arbitrary functions oftwhich related tof1,f2,f3by

and satisfy

By substituting equations(35)-(40)into the ncKPII system,we get corresponding symmetry reduction equations

along with

4.Summary

In summary,a nonlocal coupled KP system is introduced and studied by converting it into a localized system. Via this method,new solutions of the ncKP system are generated from known ones of the cKP system.An even number of singular soliton solutions are obtained in a general form,among whichN=2 andN=4 soliton solutions are plotted and analyzed.By fixing appropriate parameters, soliton solutions of the ncKPI system become breathers and we also attained lumptype solutions.The standard Lie symmetry method is carried on the ncKPII system to obtain symmetry reduction solutions.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant Nos.12175148,11975156.

Compliance with ethical standards

Conflict of interest statement

The authors declare that they have no conflicts of interest to this work.There is no professional or other personal interest of any nature or kind in any product that could be construed as influencing the position presented in the manuscript entitled.