Tsallis relative α entropy of coherence dynamics in Grover′s search algorithm
Linlin Ye, Zhaoqi Wu,∗and Shao-Ming Fei
1 Department of Mathematics, Nanchang University, Nanchang 330031, China
2 School of Mathematical Sciences, Capital Normal University, Beijing 100048, China
Abstract Quantum coherence plays a central role in Grover’s search algorithm.We study the Tsallis relative α entropy of coherence dynamics of the evolved state in Grover’s search algorithm.We prove that the Tsallis relative α entropy of coherence decreases with the increase of the success probability, and derive the complementarity relations between the coherence and the success probability.We show that the operator coherence of the firstH ⊗n relies on the size of the database N,the success probability and the target states.Moreover,we illustrate the relationships between coherence and entanglement of the superposition state of targets, as well as the production and deletion of coherence in Grover iterations.
Keywords: quantum coherence, Grover’s search algorithm, Tsallis relative α entropy of coherence
1.Introduction
Coherence is a fundamental property of quantum mechanics that stems from the quantum superposition principle.Quantification of coherence is one of the most important problems in the study of quantum coherence.Baumgratz, Gramer and Plenio [1] constituted a rigorous framework to quantify coherence from the viewpoint of quantum resource theories[2, 3] which is powerful and highly versatile.Based on this framework, some coherence measures have been proposed[4-7].An alternative framework for quantifying coherence[8] has been formulated, and some other coherence measures[9, 10] have been presented.These frameworks stimulated further research on relationships with other quantum resources [11-14], coherence dynamics and related problems[15-27], and coherence quantification in infinite-dimensional systems [28, 29].As a significant physical resource, coherence has diverse applications in biological systems [30, 31],thermodynamical systems [32-36], nanoscale physics [37],and quantum phase transition [38].
Quantum algorithms may be able to solve problems that are classically difficult.The factorization of large integers is considered to be a notoriously difficult problem on a classical device.There is no classical factorization algorithm with polynomial run-time.Shor’s quantum factorization algorithm[39] gives a superpolynomial speedup over all known classical factorization algorithms [40, 41].Hassidim and Lloyd[42]proposed the Harrow-Hassidim-Lloyd(HHL)algorithm for solving linear systems of equations and proved that any classical algorithm generically requires exponentially more time than the HHL algorithm.
The well-known Grover’s search algorithm (GSA) has been widely used in quantum information processing, which provides a quadratic temporal speedup over classical search algorithms.It has been pointed out that GSA is the repetition of the application of Grover operatorG[43], which can be decomposed intoG=H⊗nPH⊗nO,whereH,PandOare Hadamard operator,condition phase-shift operator and oracle operator,respectively.The great utility of the algorithm arises from the fact that one does not need to assume any particular structures of the database.As a crucial resource,entanglement plays a significant role[44-46]in GSA.Pan,Qiu,Mateus and Gruska [47] have shown that the oracle operatorOand the reflection operatorRcontribute to entanglement in GSA, and demonstrated that there exists a turning point during Grover’s iteration application.
Tsallis entropy [48] is an extension of Shannon entropy,which plays an important role in nonextensive statistics.Tsallis relative entropy offers an information-theoretic basis for measuring the difference between two given distributions and establishes a convergence property.Its applications in the classical system has been studied in[49-51].Quantum Tsallis relativeαentropy[52,53]is a superior information-theoretic measure of the degree of state purification compared with classical case, and it is monotonic under trace preserving completely positive linear map without the requirement that density operators are invertible [54].A quantum coherence quantifier based on Tsallis relativeαentropy has been first proposed in [55], which satisfies the monotonicity and variational monotonicity, but not the strong monotonicity.Zhao and Yu [56] proposed a modified well-defined quantifier for which the strong monotonicity holds.For Tsallis relativeαentropy, the required minimization can be solved with an explicit answer.
Noteworthily, Tsallis relativeαentropy of coherence reduces to the standard relative entropy of coherence whenα→1, and reduces to the skew information of coherence when, up to a constant factor.The relative entropy of coherence can be understood as the optimal rate for distilling a maximally coherent state from given states [2] and has a close connection with entanglement [57].The tradeoff relation of relative entropy of coherence not only depends on the state but is also accompanied by the basis-free coherence[23].The skew information of coherence has an obvious operational meaning based on quantum metrology, and forms the natural upper bounds for quantum correlations prepared by incoherent operations [6].It characterizes the contribution of the commutation between the density matrix of interest and the broken observable.The skew information andl1norm can induce the experimentally measurable bounds of coherence,while the relative entropy of coherence can be exactly measured in experiment in principle.Interestingly,Tsallis relativeαentropy of coherence andl1norm of coherence give the same ordering for single-qubit pure states [58].
The role of coherence in quantum algorithms has attracted considerable attention in recent years[59-66].It has been found that the Deutsch-Jozsa algorithm relies on coherence during the processing, and its precision is directly related to the recoverable coherence[67,68].Following their footsteps, Pan and Qiu [69] have explored the coherence dynamics of each basic operator in GSA, and the coherence production and depletion in terms of thel1norm of coherence.Likewise, similar methods have been applied to other algorithms, including the Deutsch-Jozsa algorithm and Shor’s algorithm [70], and it is found that coherence depletion always exists [70, 71].Pan, Situ and Zheng [72] have displayed the complementarity relation between coherence and the success probability in GSA via thel1norm of coherence.Coherence determines the performance of Shor’s algorithm by bounding the success probability from below and above[73].Decoherence in quantum algorithms has been studied[74-78], and coherence has been explored alongside entanglement in algorithms [74, 79-81].The role of coherence playing in the deterministic quantum computation with one qubit model has been investigated explicitly [82-86].
In this paper, we study the coherence dynamics and derive the complementarity relations between the success probability and coherence in GSA based on Tsallis relativeαentropy.The rest of the paper is organized as follows.In section 2, we recall GSA and Tsallis relativeαentropy of coherence, study the dynamics of the Tsallis relativeαentropy of coherence in GSA, and explore the complementarity relations between coherence and the success probability.In section 3, we investigate the coherence dynamics of the state after each basic operator is applied in GSA.In section 4, we study the Tsallis relativeαentropy of coherence dynamics for different cases of the target states.By identifying the variations before and after the basic operators are imposed, we explore the coherence depletion and production in section 5.In section 6,we compare our work with previous works on coherence dynamics in GSA.Finally, we summarize our results and discuss further problems in section 7.
2.Tsallis relative α entropy of coherence in GSA and complementarity relations
In section 2.1, we first review the concepts of the Tsallis relativeαentropy of coherence and GSA,and then study the coherence dynamics in GSA.We investigate the complementarity relations between coherence and success probability in section 2.2.
2.1.Tsallis relative α entropy of coherence in GSA
The Tsallis relativeαentropy is defined by [52, 53]
where
It is shown that whenα→1,Dα(ρ‖σ)reduces toS'(ρ‖σ)=ln 2S(ρ‖σ),whereS(ρ‖σ)=Tr (ρlogρ)-Tr (ρlogσ) is the standard relative entropy between two quantum statesρand σ,and the logarithm‘log’is taken to be base 2.With respect to a fixed orthonormal basisin addimensional Hilbert space, based on Tsallis relative α entropy the coherence(ρ)of a density operatorρis defined by [55]
where I denotes the set of incoherent states.It is worthwhile to note that(ρ) does not satisfy the strong monotonicity[55], and thus(ρ) is not a good coherence measure.A well-defined coherence quantifier based on Tsallis relativeαentropy has been presented forα∈ (0 ,1) ∪(1 ,2][56],
Cα(ρ) reduces to ln 2Cr(ρ) whenα→1, whereCr(ρ)=Tr (ρlogρ)-Tr(ρdiaglogρdiag) is the relative entropy of coherence [1].WhenCα(ρ) reduces to 2Cs(ρ) ,whereis the skew information of coherence [6].
LetN= 2nbe the number of elements of the database,andtthe amount of target states that meet some specific conditions in the database.The purpose of the search algorithm is to seek out the target states from the database.GSA makes use of a singlenqubit register, starts with ann-qubit pure state ∣0〉⊗nand applies the Hadamard operatorHto get an equal superposed state,
It is useful to adopt the convention that ∣χ0〉denotes the sum of all not-target states ∣xn〉,and ∣χ1〉the sum of all target states∣xs〉,
Simple algebra shows that ∣ψ〉 can be expressed as
The quantum algorithm repeats the application of a quantum subroutineG=H⊗nPH⊗nOnamed as the Grover iteration or Grover operator.Gcan be decomposed into four steps:
(i) Apply the oracle operatorO=I- 2∑xs∣xs〉〈xs∣=∑x( -1)f(x)∣x〉〈x∣.
(ii) Apply the Hadamard transform× ∣y〉〈x∣.
(iii) Perform a conditional phase shift operatorP=2∣ 0〉
(iv) Apply the Hadamard transformH⊗n.
Letρk=∣ψk〉〈ψk∣be the density operator of the state ∣ψk〉.The success probability can be expressed asPk=sin2θk.Combining equation (3) with (5), we have
Under the conditiont≪N,we have from equation (6)
· when α ∈ (0, 1),
· when α ∈ (1, 2],
Remark 2.1.Setin equation (7).The skew information of coherence of the state ∣ψk〉is given by
Under the limitα→1, from equation (6) the relative entropy of coherence of the state ∣ψk〉is
HereA≃Bmeans thatAasymptotically equals toBunder the conditiont≪N.When the success probability is increasing, according to equations (7) and(8), we obtain that the coherence is decreasing,i.e.coherence decreases with the increase of the success probability.In particular, from equation (6), when the success probability reaches 1, the coherence isIn other words,the success probability relies on the coherence depletion in terms of Tsallis relativeαentropy of coherence.
2.2.Complementarity relations between Tsallis relative α entropy of coherence and success probability
with the Bloch vectorr=(rx,ry,rz) =(sinθcosφ, sinθ×sinφ, cosθ).The Bloch vector of the original state ∣ψ〉=cosθ∣χ0〉 +sinθ∣χ1〉in GSA isr(0 ) =(sin 2θ,0,cos 2θ).Sincery=0,the Grover iterationGin the Bloch representation is given by
Afterkiterations, we have
From
we obtainrx(k) ≃-sin 2θkandrz(k)≃cos2θkwhent≪N.
Following the idea in [72], we define the normalizedαCas
Obviously,N(Cα) ∈[0, 1] .
Theorem 1.The Tsallis relativeαentropy of coherence and the success probability satisfies the following complementary relations in GSA fort≪N.
(1) Forα∈ (0 ,1), it holds that
(2) Forα∈ (1 ,2], it holds that
where ≃means the algorithm search in a large database satisfyingt≪N.
Proof.Sincerx(k) ≃-sin 2θkandrz(k)≃ cos 2θk,simple calculation yields thatandAccording to equation (6), we have
Whenα∈ (0, 1),t≪N,we obtain
Sincerz(k) ∈[0, 1] ,the maximum ofCαis
Then we have
Whenα∈ (1, 2],t≪N,we obtain
Sincerz(k) ∈[0, 1] ,we have
and
Remark 2.2.Whenin equation (12), the complementarity relation between skew information of coherence and success probability is of the form,
At the limitα→1, equation (6) gives rise to
Whenrz=1,we have
According to equations (12) and (13), whenα∈ (0, 1)andPk=1,normalization of coherence satisfiesWhenα∈ (1, 2] andPk=1,normalization of coherence satisfiesN(Cα) ≃0.Noting thatN(Cα)is the normalization ofCα,andA≃Bmeans thatAis asymptotically equal toBunder the conditiont≪N,this does not necessarily mean thatCαis asymptotically equal to 0, let alone it is equal to 0.
3.Dynamics of the Tsallis relative α entropy of coherence in GSA
In this section, we investigate the coherence of the state after each basic operator is applied in the Grover iteration.
Denote the firstH⊗nand the secondH⊗nbyHOandHP,respectively.In [21,87] it has been shown thatis the general form of any of the unitary incoherent operators, whereβ(i) is relabeling of {i}.Hence,the oracle operatorOand the condition phase-shift operatorPare incoherent operators.Moreover, bothOandPdo not change the coherence.Denote ∣ψkO〉the state afterOis applied on ∣ψk〉andρkO=∣ψkO〉〈ψkO∣.We have
Combining equation(3)with(5),we haveCα(ρkO)=Cα(ρk),whereα∈ (0, 1) ∪(1, 2].
In the computational basis,theN-dimensional Hadamard matrix has the following three properties: (i) The common coefficient is(ii) The elements of the first row and the first column are 1.(iii) In any other rows or columns, a half of the elements are 1, and the others are-1.LetHy,xdenote the element of theyth row and thexth column in a Hadamard matrix andtydenote the number ofHy,x=1,ty=∣{Hy,x∣Hy,x=1,x∈{xs}}∣.Denote by ∣ψkHO〉the state afterHOis applied on ∣ψkO〉and ∣ψkHP〉the state afterHPis applied onPH⊗n∣ψkO〉.We have
and
Theorem 2.The Tsallis relativeαentropy of coherence of the states ∣ψkHO〉and ∣ψkHP〉are given by
and
respectively fort≪Nandα∈ (0, 1), and
and
respectively fort≪Nandα∈ (1, 2] ,whereγ(t,ty)=andPk=sin2θk.
Proof.From equation (21) ∣ψkHO〉can be reexpressed as
According to equation (22), we obtain
By straightforward derivation we have
andρkHP=∣ψkHP〉〈ψkHP∣=ρk+1.
Combining equation (3) with (29) we have
SinceρkHP=ρk+1,we haveCα(ρkHP)=Cα(ρk+1) and
Remark 3.1.Setin equations(23)and(24).The skew information of coherence of the states ∣ψkHO〉and ∣ψkHP〉satisfy
respectively.Whenα→1 in equation (30), according to equation (10), the relative entropies of coherence of the state∣ψkHO〉 and ∣ψkHP〉satisfy
respectively.Based on Theorem 2, it is easy to see that the coherence of the state ∣ψkHO〉is related to the size of the databaseN, success probabilityPkand target states.The coherence of the state ∣ψkHP〉is dependent onNandPk.
4.Different target states
In this section,we discuss the coherence of the state ∣ψkHO〉for special target states, i.e.the superposition state ∣χ〉1is a product state, and the target numbers aret≤ 4.We have the following result.
Theorem 3Suppose that the superposition state ∣χ〉1is a product state.Then whent≪Nthe Tsallis relativeαentropy of coherence of the state ∣ψkHO〉is given byforα∈ (0, 1), and
forα∈ (1 ,2].
Proof.Denote ∣χ0H〉 =H⊗n∣χ0〉and ∣χ1H〉 =H⊗n∣χ1〉.Sinceis the product ofnsingle-qubit states of the forms either ∣0〉 ,∣1〉 orcan be written as
and
where
and
After a simple transformation, we have
and
Consequently, we derive that
Whent≪N,α∈ (0, 1) ,andPk=sin2θk,we have
and whent≪N,α∈ (1 ,2],Cα(ρkHO) takes the form
This completes the proof.□
In addition,for the case that ∣χ〉1is a product state,t≪Nandin equation (34), the skew information of coherence of the state ∣ψkHO〉is given by
Taking the limitα→1 in equation (40), the relative entropy of coherence of the state ∣ψkHO〉is given by
We now explore the coherence of the state ∣ψkHO〉when the number of the target states is small (t≤ 4).
· Whent= 1, the database has one single target state,∣χ〉1is always a product state.According to Theorem 3 we get
whenα∈ (0 ,1), and
whenα∈ (1 ,2].
·Whent= 2,we denote the two target states by ∣x11〉and∣x12〉,respectively.We have ∣t-2ty∣=1for either ∣x11〉 =0 or∣x11〉 ≠0[69].Thus
(1) Whenα∈ (0 ,1), according to equation (23)we have
(2) Whenα∈ (1 ,2], according to equation (25) we obtain
(1) According to equation (23) we get
forα∈ (0 ,1),
(2) for α ∈(1, 2],
· Whent= 4,there are two cases that ∣χ〉1is either a product state or not.
Case 1: ∣χ〉1is a product state.It is observed that∣t-2ty∣=1[69] and
(1) Whenα∈ (0,1 ) we obtain
(2) Whenα∈ (1 ,2] the coherence of the state ∣ψkHO〉is
Case 2: ∣χ〉1is not a product state.It is observed that[69] and
(1) Whenα∈ (0,1 ) we have
(2) Whenα∈ (1 ,2] ,the coherence of the state ∣ψkHO〉is
Remark 4.1.(1) Whent= 1 andin equation (45),according to equation(44)the skew information of coherence and the relative entropy of coherence of the state ∣ψkHO〉are
respectively.
(2) Whent= 2,in equation (47), according to equation (33) the skew information of coherence and the relative entropy of coherence of the state ∣ψkHO〉are
respectively.
(3) Whent= 3 andin equation.(49), according to equation (33) the skew information of coherence and the relative entropy of coherence of the state ∣ψkHO〉are
respectively.
(4) Whent= 4, there are two cases.
respectively.
respectively.
According to Theorem 3 and equations (51), (52), (53)and (54), whenα∈ (1,2 ] the Tsallis relativeαentropy of coherence of the state ∣ψkHO〉is larger when the superposition state of the targets is an entangled one.However, whenα∈ (0,1 ) it is found that the coherence is smaller when the superposition state of the targets is entangled.
ConjectureThe Tsallis relativeαentropy of coherence of the staterelies on the size of the databaseN, the success probability and the target states.
(1) Forα∈ (0 ,1) ,the coherence of ∣ψkHO〉reaches the lower bound whent=1,and the coherence of ∣ψkHO〉reaches the upper bound when ∣χ〉1is a product state.It holds that
(2) Forα∈ (1 ,2] ,the coherence of ∣ψkHO〉reaches the upper bound whent=1, and the coherence of ∣ψkHO〉reaches the lower bound when ∣χ〉1is a product state.It holds that
5.Production and depletion of Tsallis relative α entropy of coherence
The coherence of a state changes when the operatorsHPandHOare applied.In this section, we investigate how the coherence changes before and after these operators are applied, i.e.the production and depletion of the Tsallis relativeαentropy of coherence forα∈ (1, 2].In order to clarify the variations and connections of operator coherence in GSA,we also provide some examples and diagrammatic sketches related to the coherence dynamics.
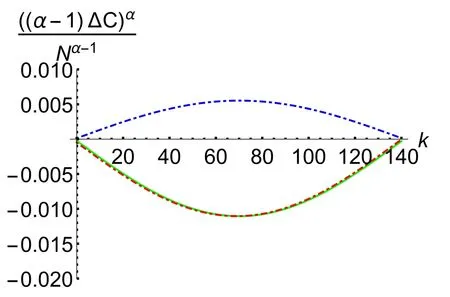
We first introduce the following definitions.The variations of operator coherence between two consecutive iterations ofHO,HPandGin GSA are defined as
The variations of suboperator coherence of each basic operatorHOandHPin one Grover iteration are defined as
Concerning the production and depletion of coherence for basic operators in GSA, we have the following conclusion.
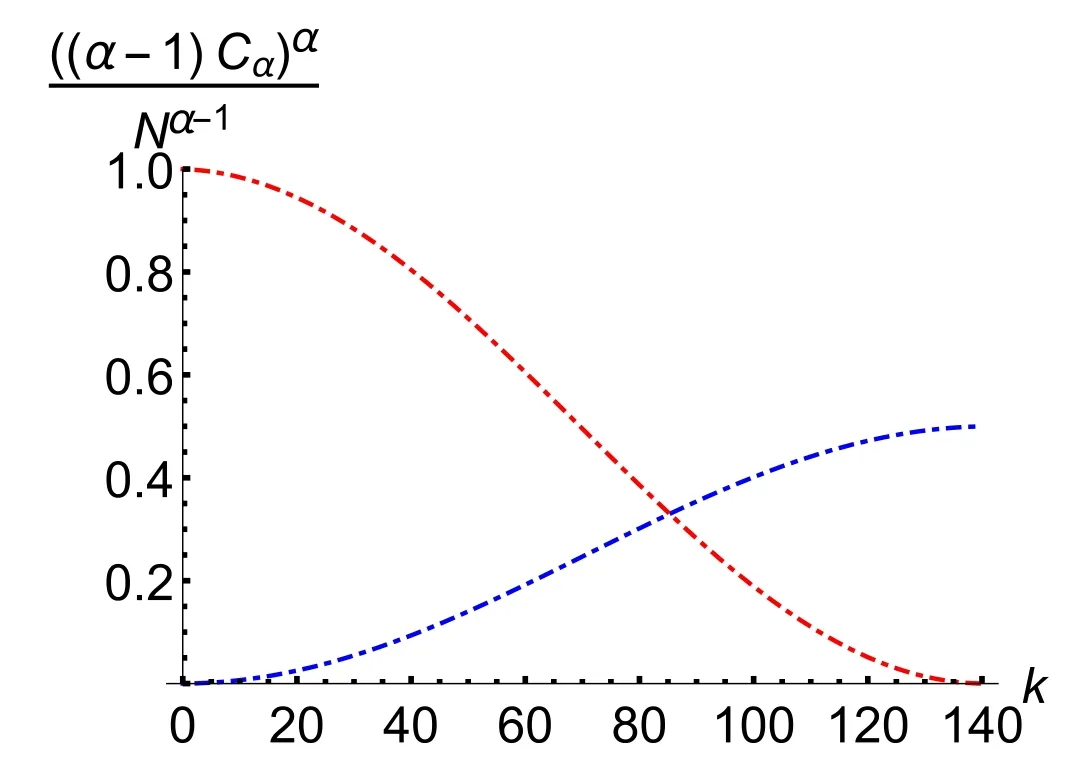
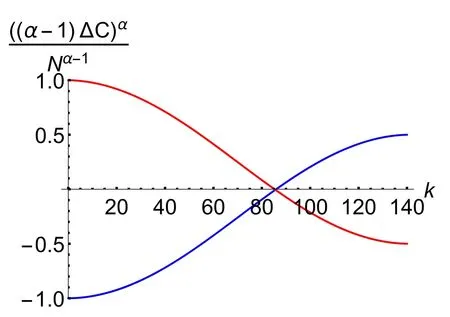
Theorem 4.Forα∈ (1,2 ]andt≪N,the variations and connections of operator coherence between two consecutive iterations ofHO,HPandGin GSA are given by
and
Proof.Combining equations (8) with (55), it is easy to obtain
SincePk Similarly, according to equations (25) and (56), it is easy to get Combining equations (26) with (57), we have Obviously, we have the following relationship among these variations, According to Theorem 4,the operator coherence between two consecutive iterations ofHPandGis depleted.Both of them rely on the size of the databaseNand the success probability.Correspondingly, the operator coherence between two consecutive iterations ofHOis produced,which relies on the size of the databaseN, the success probability and target states. Theorem 5.Forα∈ (1,2 ] andt≪N,the functions ΔCα(ρkHP) and ΔCα(ρkHO) have a turning point.The variations of the suboperator coherence of each basic operatorHOandHPin one Grover iteration are given by Proof.According to equations (8), (25) and (58), we have (62).Similarly, by substituting equations (25) and (26)into (59), we obtain (63).There exists a turning pointkTat which ΔCα(ρkΔHO)=0.This is equivalent to(γ(t,ty)+1)Pk- 1=0,namely, Similar results can be obtained for ΔCα(ρkΔHP)=0.□ According to Theorem 5, fort≪Nwe have ΔCα(ρkΔHO)<0 and ΔCα(ρkΔHP)>0when (γ(t,ty)+1)Pk<1,and ΔCα(ρkΔHO)>0 and ΔCα(ρkΔHP)<0when(γ(t,ty)+1)Pk>1.The Tsallis relativeαentropy of coherence ofHOandHPshow different effects that one depletes coherence and the other produces coherence.Moreover, the operator coherence ofH⊗nis not always produced or depleted, but depleted and produced alternatively.Before the turning point, the operator coherence ofHOis depleting, and the operator coherence ofHPis producing.However, the situation is reversed after the turning point. We now use examples and plots to illustrate the characters of coherence of the state after each basic operator is applied in GSA,how these operators contribute to coherence,and the relationships among the coherence of the operators and the success probability. Example 1Suppose that the qubit numbers aren= 16 and the target numbers aret= 2.In this caseBased on Theorem 5,the suboperator coherence ofOandPin one Grover iteration are unaltered.Whenk Figure 1.The coherence dynamics in one Grover iteration.The red, blue, black and green dots are the coherences ofO, HO ,P and HP ,respectively.The variations of the suboperator coherence before the turning point(a),at the turning point(b)and after the turning point(c). Figure 2 shows that the success probabilityPkincreases with the increase of the number of iterations.According to equations (25) and (26), the operator coherence ofH⊗nvibrates between 1-Pk+1andγ(t,ty)Pk.The relations between the operator coherence ofH⊗nand the operator coherence ofHOandHPare shown in figure 3.The intersection of the two lines is the turning point. Figure 2.The variations of success probability Pk (red dot-dashed line) as a function of the number of iterations k. Figure 3.The operator coherence ofH ⊗n .The blue dot-dashed line and red dot-dashed line represent the operator coherence of HO and HP ,respectively. Figure 4.The operator coherence ofG (green), HP (red dot-dashed)and HO (blue dot-dashed) between two consecutive iterations. Figure 5.The suboperator coherence of HP (red) and HO (blue) in one Grover iteration. Figure 6.Subfigures (a)-(f) are for the case that the superposition state of targets is a product one (an entangled one).(a), (d) The relationships of the operator coherence of HP and HO .(b), (e) The relationships of ΔCα(ρ kG),ΔCα(ρkHP) and ΔCα(ρkHO) between two consecutive iterations.(c), (f) The connections of the suboperator coherence of HP and HO in one Grover iteration. In figure 4, we illustrate the relationships of ΔCα(ρkG),ΔCα(ρkHP) and ΔCα(ρkHO) between two consecutive iterations. According to Theorem 3, we have ΔCα(ρkG)≃which are zero at the beginning and the end.The connections of the suboperator coherence ofHPandHOin one Grover iteration are shown in figure 5.Moreover,the coherence ofHP(HO)is 1(-1)at the beginning andat the end. Example2Consider that the qubit numbers aren= 18 and the target numbers aret= 4.In this casewhen the superposition state of targets is entangled andwhen superposition state is a product one.From Theorem 3 the Tsallis relativeαentropy of coherence of∣ψkHO〉is larger when the superposition state of targets is entangled forα∈ (1 ,2].When the superposition state of targets is entangled, we show in figure 6 the relationships between the operator coherence ofHPandHO,the relationships among ΔCα(ρkG),ΔCα(ρkHP) and ΔCα(ρkHO) between two consecutive iterations, and the connections between the suboperator coherence ofHPandHOin one Grover iteration.For comparison, we also present the corresponding results when the superposition state of targets is a product one. Note that Tsallis relativeαentropy of coherence incorporates two important coherence quantifiers, the relative entropy of coherence and the skew information of coherence,so using such technical methods of Tsallis relativeαentropy to study coherent dynamics may yield more information about the properties of different coherent measures in GSA.It can also be seen from the examples that entanglement has an important contribution to operator coherence in GSA. In order to clarify the contribution of this paper, we compare our work with previous related works in this section. In [69], the authors have investigated thel1norm of coherence of the states after each ofO,PandH⊗nis applied in oneGiteration,and discussed the number of coherence for different cases of the target states.It is shown that the coherence is monotone decreasing with the increase of the success probability, and it is proved that the coherence is vibrating, the overall effect is that coherence is in depletion.Moreover, the coherence is larger when the superposition state of targets is an entangled one. In this work,we study coherence dynamics in GSA based on Tsallis relativeαentropy.The amount of coherence of firstH⊗ndepends on the size of the databaseN, success probability and target states,and the coherence of twoH⊗nhave different effects that one depletes coherence and the other produces coherence.Coherence is not always produced or depleted,but depleted and produced in turn.Whenα∈ (0 ,1),the coherence is smaller when the superposition state of targets is an entangled one, and the coherence reduction is not monotonic,but related to the parameterαwith the increase of the success probability, which is different from [69]. On the other hand,in[47],the Grover iteration has been decomposed into two basic operatorsRandO, whereR=H⊗nPH⊗n.It is demonstrated thatH⊗ndoes not change entanglement, and there exists a turning point during the application of the algorithm.Before the turning point, the entanglement always increases when the operatorOis applied,and the effect of the operatorRcan be almost ignored on the level of entanglement.After the turning point, theRremarkably decreases entanglement, andOincreases entanglement.In our work,we study the coherence of the states on the essential operator level and show that operatorsOandPdo not change the coherence.In addition, we also obtain a turning point whenα∈ (1 ,2].Before the turning point, the operator coherence ofHOis depleting, and the operator coherence ofHPis producing.After the turning point, the situation is reversed. We have explored the coherence dynamics in GSA based on Tsallis relativeαentropy forα∈ (0 ,1) ∪(1 ,2] ,and proved that the coherence decreases with the increase of the success probability.We have derived the complementarity relations between Tsallis relativeαentropy of coherence and the success probability.Moreover, we have studied how each basic operator contributes to the coherence in GSA, and proved that the amount of operator coherence ofHOrelies on the size of the databaseN, the success probability and the target states.Following the idea in [69], we have also discussed the operator coherence of ∣ψkHO〉for different target states.Finally, whenα∈ (1 ,2], we have derived the variations of operator coherence between two consecutive iterations ofHO,HPandGin GSA, and the variations of suboperator coherence of each basic operatorHOandHPin one Grover iteration.The operatorsHOandHPhave different effects on coherence, one produces coherence and another depletes it.Coherence of theH⊗nis not always depleted but depleted and produced alternatively.It oscillates during GSA application. In addition, whenα∈ (0,1 ) andα∈ (1 ,2], the entangled target state has different impacts on the Tsallis relativeαentropy of coherence.Whenα∈ (0 ,1), the coherence is smaller when the superposition state of targets is an entangled one.However,whenα∈ (1 ,2], the coherence is larger when the superposition state of targets is an entangled one.It would be interesting to study how the entanglement of the superposition state of targets is related to the coherence quantitatively.Our results may shed some new light on the study of the coherence dynamics in quantum algorithms, and provide new insights into quantum information processing tasks. Utilizing the relative entropy of coherence and thel1norm of coherence, it has been pointed out in [70] that coherence of the system states reduces to the minimum in company with the successful implementation of Grover’s algorithm.In this paper, we can draw the same conclusion when the Tsallis relativeαentropy of coherence is employed.Nevertheless, a similar assertion does not hold if other quantifiers of a resource, like quantum entanglement, are used.This peculiar character of quantum coherence may be beneficial for designing new quantum algorithms in the future. Acknowledgments The authors would like to express their sincere gratitude to the anonymous referees,which greatly improved this paper.This work was supported by the National Natural Science Foundation of China (Grant Nos.12161056, 12075159,12171044); Beijing Natural Science Foundation (Grant No.Z190005); the Academician Innovation Platform of Hainan Province. Competing interests The authors declare no competing interests.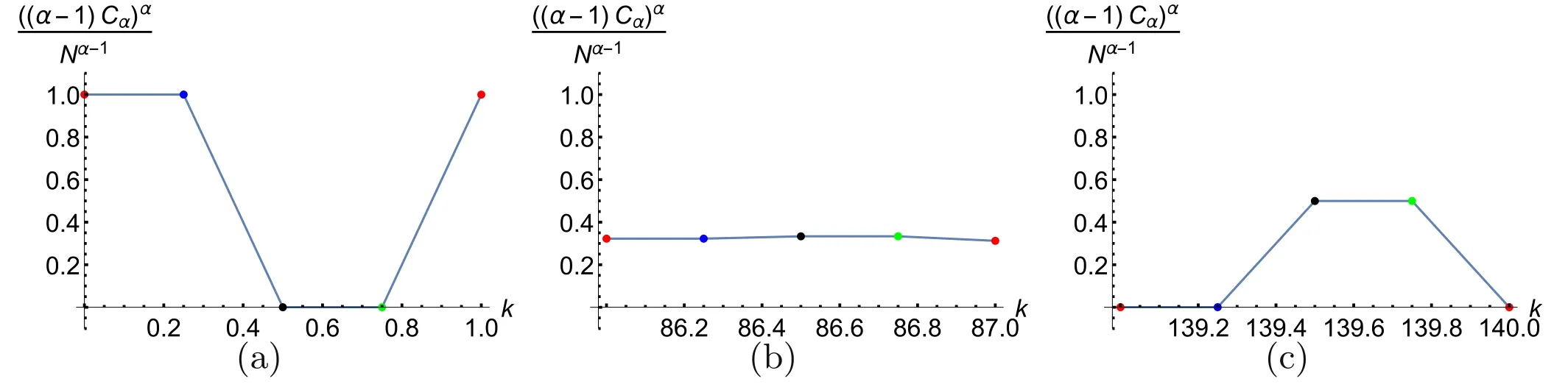


6.Comparison with previous works
7.Conclusions and discussions
 Communications in Theoretical Physics2023年8期
Communications in Theoretical Physics2023年8期
- Communications in Theoretical Physics的其它文章
- On the emergence of gravitational dynamics from tensor networks
- Ordered exponential and its features in Yang-Mills effective action
- Searching for a0(980)-meson parton distribution function
- A study on stochastic longitudinal wave equation in a magneto-electro-elastic annular bar to find the analytical solutions
- Multiple soliton solutions and symmetry analysis of a nonlocal coupled KP system
- Painlevé analysis, infinite dimensional symmetry group and symmetry reductions for the (2+1)-dimensional Korteweg-de Vries-Sawada-Kotera-Ramani equation
