A study on stochastic longitudinal wave equation in a magneto-electro-elastic annular bar to find the analytical solutions
M Mamun Miah, M Ashik Iqbal and M S Osman
1 Department of Mathematics, Khulna University of Engineering and Technology, Khulna-9203,Bangladesh
2 Division of Mathematical and Physical Sciences, Kanazawa University, Kakuma, Kanazawa 920-1192,Japan
3 Department of Mathematics and Physics, Khulna Agricultural University, Khulna-9100, Bangladesh
4 Department of Mathematics, Faculty of Science, Cairo University, Giza 12613, Egypt
Abstract In this paper, we set up dynamic solitary perturb solutions of a unidirectional stochastic longitudinal wave equation in a magneto-electro-elastic annular bar by a feasible, useful, and influential method named the dual (G '/G, 1/G)-expansion method.Computer software, like Mathematica, is used to complete this discussion.The obtained solutions of the proposed equation are classified into trigonometric,hyperbolic,and rational types which play an important role in searching for numerous scientific events.The technique employed here is an extension of the(G '/ G)-expansion technique for finding all previously discovered solutions.To illustrate our findings more clearly, we provide 2D and 3D charts of the various recovery methods.We then contrasted our findings with those of past solutions.The graphical illustrations of the acquired solutions are singular periodic solitons and kink solitons which are added at the end of this paper.
Keywords: dual (G'/G, 1/G)-expansion method, stochastic longitudinal wave equation,dynamic solitary perturb solutions, magneto-electro-elastic annular bar
1.Introduction
Most of the events occurred in nature are modeled by nonlinear partial differential equations (NLPDEs), especially in the science and engineering.Therefore, we are looking for the solutions of NLPDEs to give the scientific explanation of all the occurrences occurred in nature especially in the region of applied science,engineering,quantum physics,plasma physics,solid-state physics, plasma waves, fluid mechanics, electrodynamics, string theory, chemistry, biology, general relativity,astrophysics, biological science, genetic science, and others[1-45].In the research community, many researchers have constructed different kinds of formulae to find the exact dynamic wave solutions of NLPDEs such as the Jacobi elliptic expansion method [1, 2], the new auxiliary equation method[3], the F-expansion method [4], the direct algebraic method[5], the tanh-function method [6, 7], the Hirota’s bilinear transformation method [8, 9], the homogeneous balance method [10, 11], the tanh/coth method [12, 13], the first integral method [14, 15], the finite different approach [16], the auxiliary equation method [17], the exp(-φ(ξ))-expansion method[18,19],the exponential function method[20,21],the variational iteration method [22], the Lie group method [23],the generalized Kudryshov method [24-26], the Cole-Hopf transformation method [27], the Backlund transform method[28], the Riccati equation method [29], the (G'/G)-expansion method [30-32], the improved(G'/G)-expansion method[33, 34], the generalized (G'/G)-expansion method [35], the modifeid(G'/G)-expansion method [36], the enhanced(G'/G)-expansion method [37] and others [38-45].
Lately, Miahetal[46] and Mustafaetal[47] have proposed dual (G'/G, 1/G)-expansion method to solve the integro-differential equations and the Kaup-Kupershmidt equation, respectively.Furthermore, many of the researchers[48-50] have applied this method to solve the NLPDEs.In this work,we discuss the dynamic solitary perturb solution of the unidirectional stochastic longitudinal wave equation in an magneto-electro-elastic (MEE) annular bar.To track down and interpret the various kinds of traveling wave and coefficient function solutions to the stochastic longitudinal wave equation in an MEE annular bar, we have used the dual(G'/G, 1/G)-expansion method.And effectively, we set up many new and simpler traveling wave and coefficient function solutions together with soliton type’s solutions, trigonometric function solutions, hyperbolic function solutions, and rational function solutions.The unidirectional stochastic longitudinal wave equation in an MEE annular bar has the following form:
whereu=u(x,t) is the longitudinal displacement function,v0is the velocity of wave, andnis the diffusion parameter which are all influenced by the rod’s geometry and material characteristics.The unidirectional stochastic longitudinal wave equation in an MEE annular bar has been studied using a variety of computational strategies(Maetal[51]and Khanetal[52]).We believe that the double(G'/G,1/G)-expansion method has not yet been used to study this model.
Our article is designed in the following manners: introduction is stated in section 1.In section 2, the dual(G'/G, 1/G)-expansion method has been investigated.In section 3, the dual(G'/G, 1/G)-expansion method is applied to discuss different solutions of the given unidirectional nonlinear longitudinal wave equation.In section 4, the graphical representations of the attained solutions are provided.The conclusion is given in the last section.
2.Interpretation of the dual (G′/G, 1/G)-expansion method
In this section, we analyze the dual (G'/G, 1/G)-expansion method.To this end, we take into account a linear ordinary differential equation of order two:
and taking the two new functions with the following assumptions:
From equations (2.1) and (2.2), we can set up the next two connections betweenYandZas the following:
Based on the signs ofλ, equation (2.1) gives three categories of solutions which are given below,
Category 1.Forλ> 0, we get a trigonometric function solution of equation (2.1) as
and hence, we get
wherer1=μ12+μ22andμ1andμ2are constants.
Category 2.Forλ< 0, we have a hyperbolic function solution of equation (2.1) as
and hence, we get
wherer2=μ12-μ22.
Category 3.Forλ= 0, a rational function solution has been obtained from equation (2.1) which is given below
and we get
Now, we assume an NLPDE with a polynomialPinu(x,t) and its partial derivatives as the following:
Now, we will discuss the dual (G'/G, 1/G)-expansion method step by step in the following way.
Step I.By using the conventional wave transformation method, we transform the functionuas a function of single parameter as
wherefandcimply the frequency and wave number respectively.
Now,the corresponding ordinary differential equation of equation (2.11) is given below,
whereOis a polynomial inuζ( ) and its derivative regarding toζ.
Step II.We write the solution of equation (2.12) as a combination of the function ofY(ζ)andZ(ζ)in the following formatand the constantsa i(i=0, 1, 2, …,Q),bi(i=1, 2, …,Q)andc,λ,mcan be found by step III.The balance number can be found from the heights order derivative and heights order nonlinear term by the homogenous balance rule.Again,by substituting the required balance number in equation (2.13) and plugging this reformed equation into equation (2.12) and by using equations (2.3) and (2.5) (by considering category 1 as an example), we transform the left hand part of equation(2.12)in the function ofYandZ,where the degree of Z cannot be greater than one and the degree ofYcan be taken from zero up to any positive integer value.
Step III.By balancing the same power of the given expression from the two sides, we obtain a pattern of algebraic solutions in terms ofai,bi,c,λ,m,μ1, andμ2.Now,we can use any computation software(Mathematica or Maple)to get the solution of the required algebraic system.By inserting the required values into equation (2.13), we get the solutions of equation (2.12) and also by putting the valueζ=f(x-ct) in the solutions of equation (2.12), we get the desirable dynamic wave solutions of equation (2.10).
3.Solutions of stochastic longitudinal wave equation in an MEE annular bar
In this part, we apply the dual(G'/G, 1/G)-expansion method to trace the constructive solutions of the given longitudinal wave equation.By applying wave conversion method cited in equation(2.11),we transform the longitudinal wave equation given in equation (1.1) into a nonlinear ordinary differential equation as follows:
Integrating equation(3.1)for two times and omitting the constants of integration, we get
where the prime refers to the derivatives with respect toζ.
By using the homogeneous balance method in equation (3.2), we get the balance numberQ= 2 and inserting this balance number in equation(2.13),we have the following form
wherea i(i=0, 1, 2) andbi(i=1, 2) are constant coefficients and the functionsYζ( ) andZ(ζ) are given by equation (2.3).Now, for three signs of λ, we get the basic three pattern of solutions of equation (3.2) which are given below periodically.
Case 1.For λ > 0.
After differentiating of equation (3.3) for two times and with the help of equations (2.3) and (2.5), we transform the left side of equation(3.2)in terms ofYandZand then setting the coefficients of the acquired expression identical zero, we get three pairs of algebraic equations ina0,a1,a2,b1,b2,λ,f, andc.Now,by using the computer program Mathematica,we gain two sets of solutions as follows
Set 1:
Set 2:
By setting these values from the above two sets into equation (3.3), we attain the solutions of equation (3.2).By using set 1, we have
Again, choosingμ2= 0,m=0 andμ1≠0,we have another particular solution of equation (1.1) as follows
By the same way, using equation (3.5) in equation(3.3),we get the following equation:
Now, forμ2= 0,m=0 andμ1≠0,we have one more particular solution of equation (1.1) as follows
Case 2.For λ < 0.
Similar to condition 1, we attain two sets of solutions as follows
Set 1:
Set 2:
Substituting the values of the sets of constants from equations (3.12) and (3.13), respectively into equation (3.3),we get the solution of equation(3.2).Now,for set 1,we have solution as follows
Again, for set 2, we have another solution of equation (3.2) as follows
Case 3.For λ = 0.
In this case, only one set of values of arbitrary constants exists which is given below
Using equation (3.18) in equation (3.3), we get the solution of equation (3.2) as follows
Now,we placeζ=f(x±v0t)in equation(3.19)and we chooseμ2= 0,m=0 andμ1≠0,then we have a rational function solution of equation (1.1) as follows
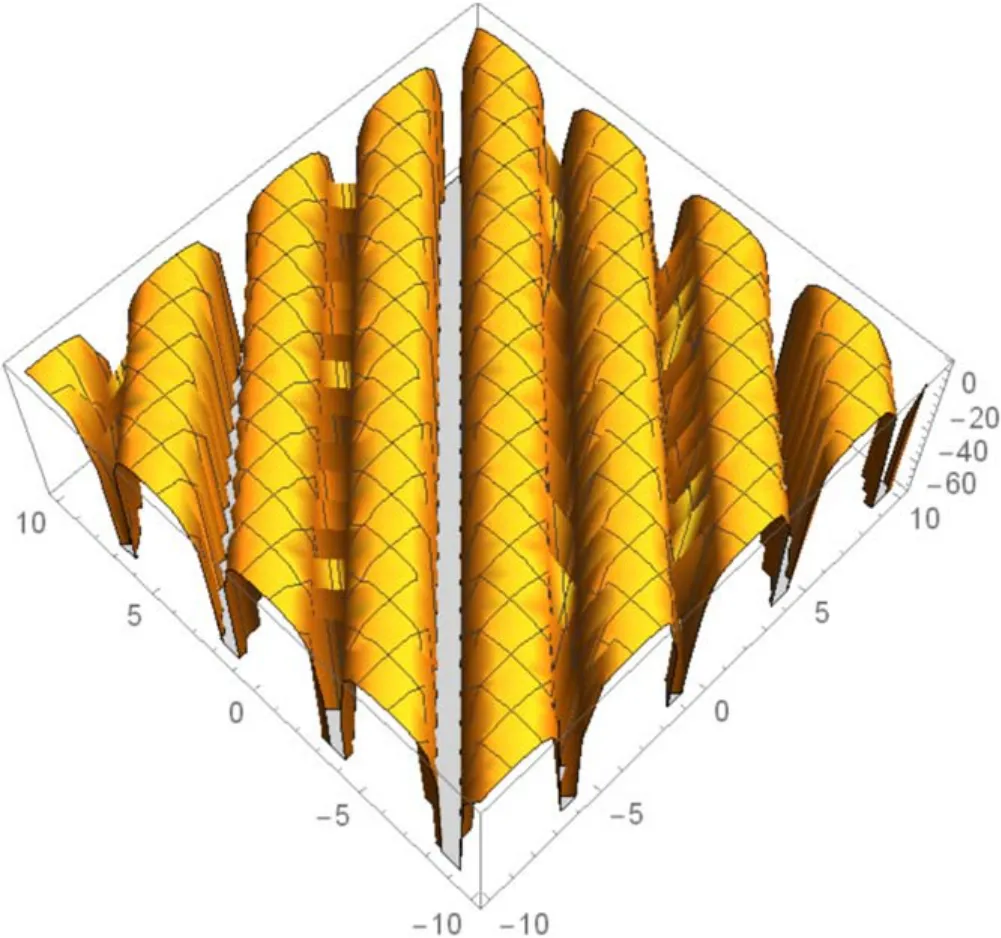
Figure 1.The 3D figure in equation (3.7) implying the singular periodic soliton for c =1, v0=2,n =2.
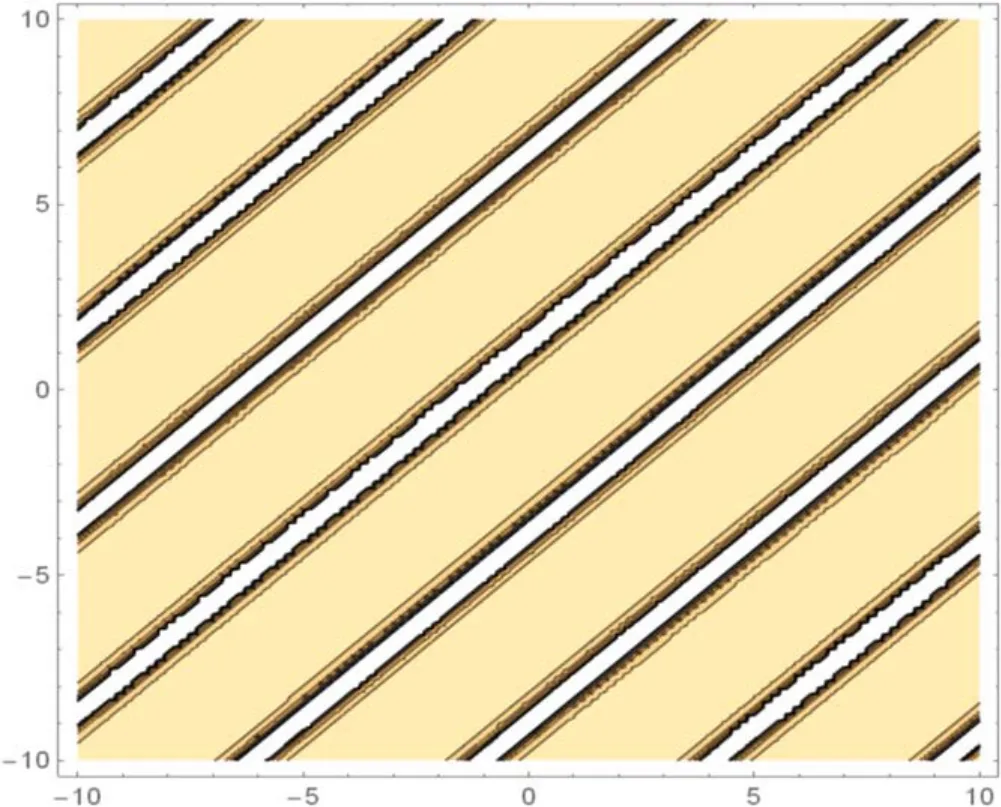
Figure 2.The contour figure in equation (3.7) for c= 1,v0=2,n =2.
4.Numerical simulation results with discussion
In this section, the physical explanation of the obtained solutions of the unidirectional nonlinear longitudinal wave equation in a MEE annular rod has been presented.The acquired solutions are classified into trigonometric, hyperbolic, and rational function types with the aid of the Mathematica program.These solutions are sketched in 3D, contour and 2D plots which are given in figures 1-15 through the intervalsx∈ [-10, 10] andt∈ [-10, 10] .The given 3D shapes imply the structure of a singular periodic soliton and singular kink shape soliton.For the valuesc=1,v0=2,n=2;c=2,v0=1,n=3 andc=2,v0=1,n=1, in figures 1, 4, and 10 the solutions in equations (3.7), (3.11),and equation(3.17),respectively exhibit the singular periodic solitary wave solution and its similar contour shapes are in figures 2, 5, and 11.Further, fort= 1,t= 2, andt= 2, we obtain similar 2D graphs in figures 3,6,and 12,respectively.Similarly, forc=2,v0=1,n=1 andv0=1,n=2, in figures 7 and 13 the solutions in equation (3.15) and in equation (3.20) show the singular kink soliton and its corresponding contour shapes in figures 8 and 14.Also, fort=1 andt=2, we get a similar 2D graph in figures 9 and 15, respectively.

Figure 3.The 2D surface in equation (3.7) for c =1, v0=2,n =2, t =1.
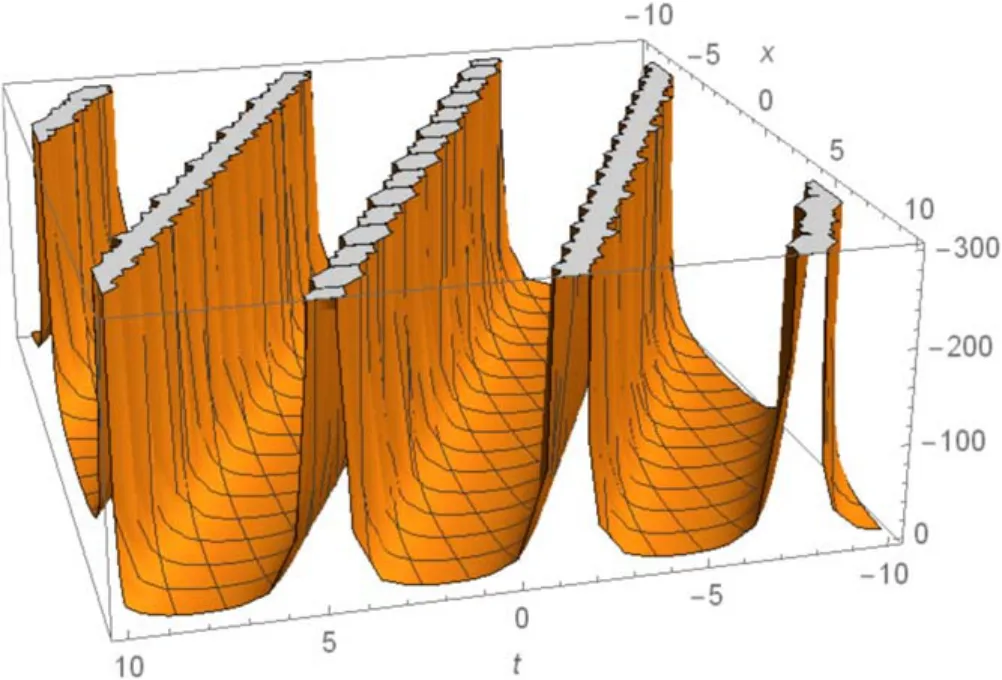
Figure 4.The 3D shape in equation (3.11) implying the singular periodic solitary wave solution for c =2, v0=1,n =3.
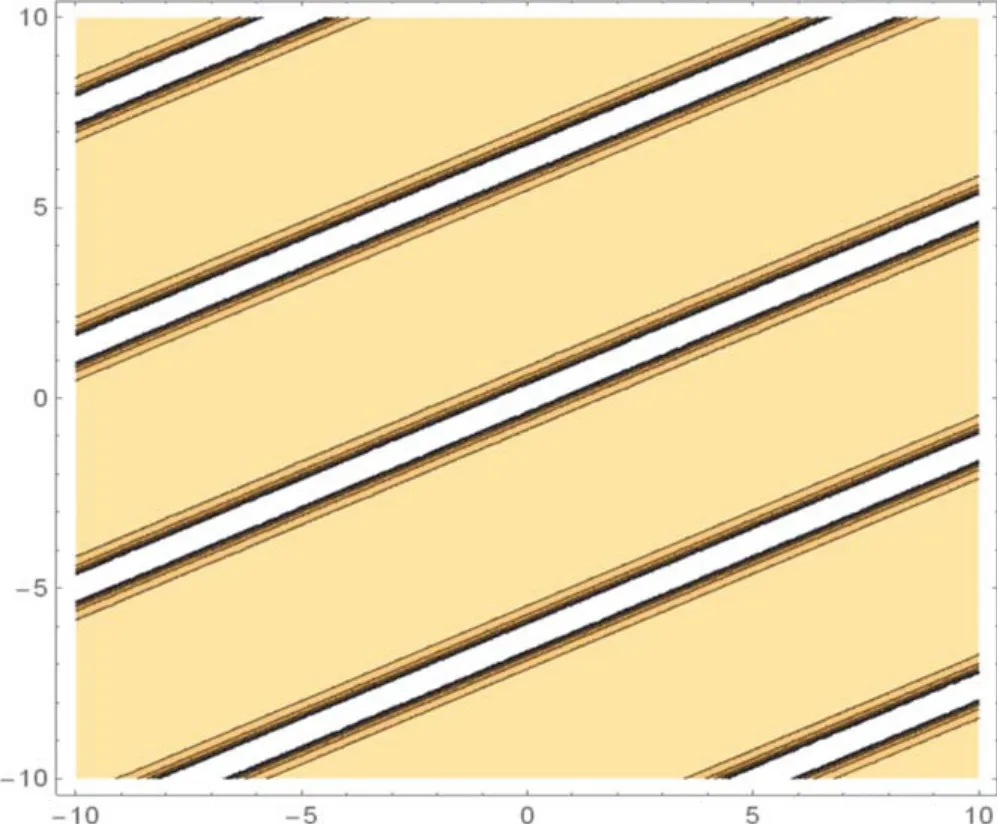
Figure 5.The contour graph in equation (3.11) for c =2,v0=1,n =3.
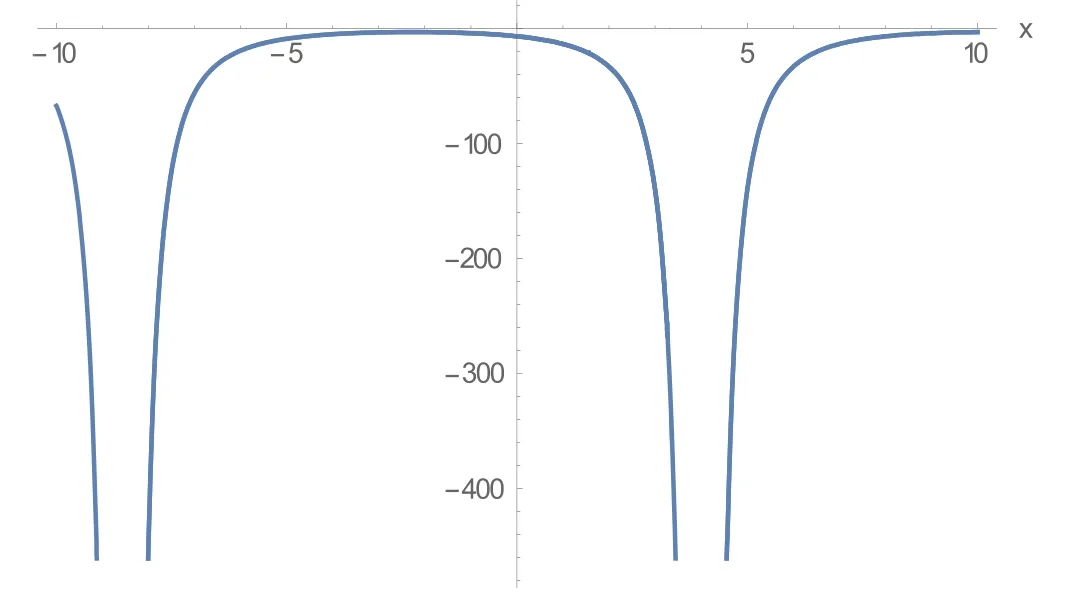
Figure 6.The 2D graph in equation(3.11)for c =2, v0=1,n =3,t =2.
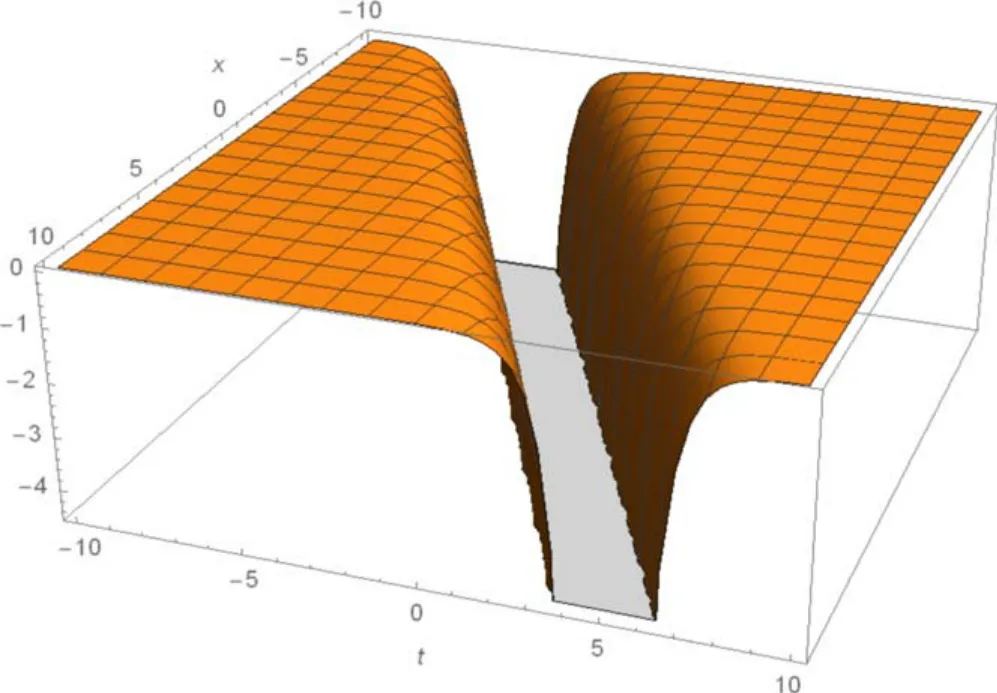
Figure 7.The 3D structure in equation(3.15)indicating the singular kink shape soliton for c =2, v0=1,n =1.
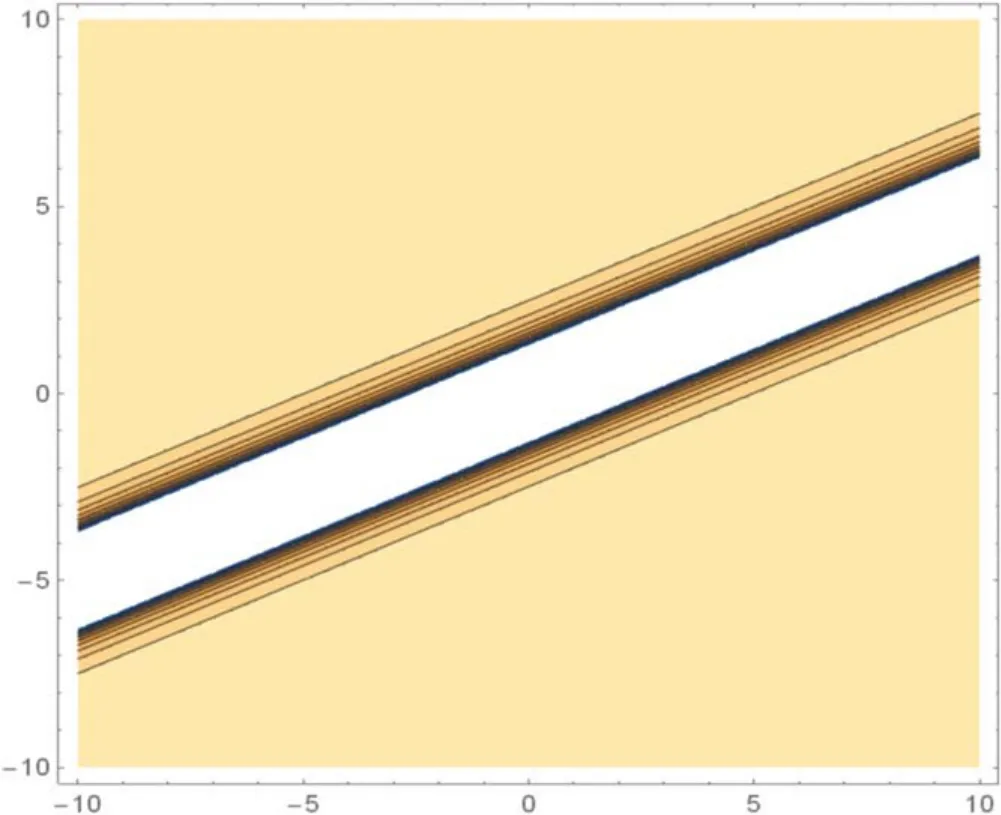
Figure 8.The contour figure in equation (3.15) for c =2,v0=1,n =1.
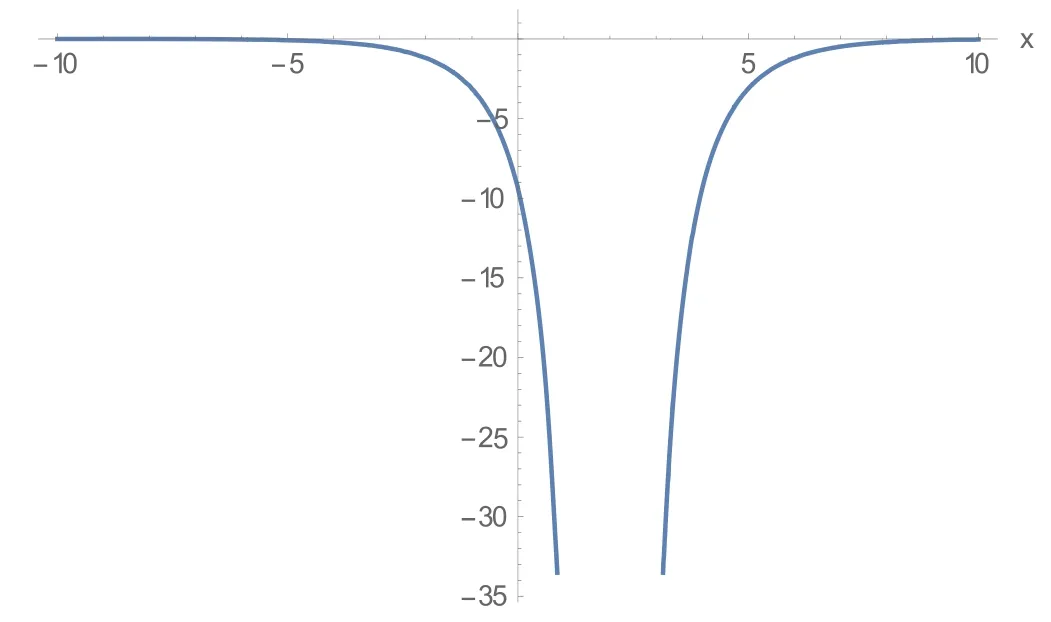
Figure 9.The 2D structure in equation (3.15) for c =2, v0=1,n =1, t =1.
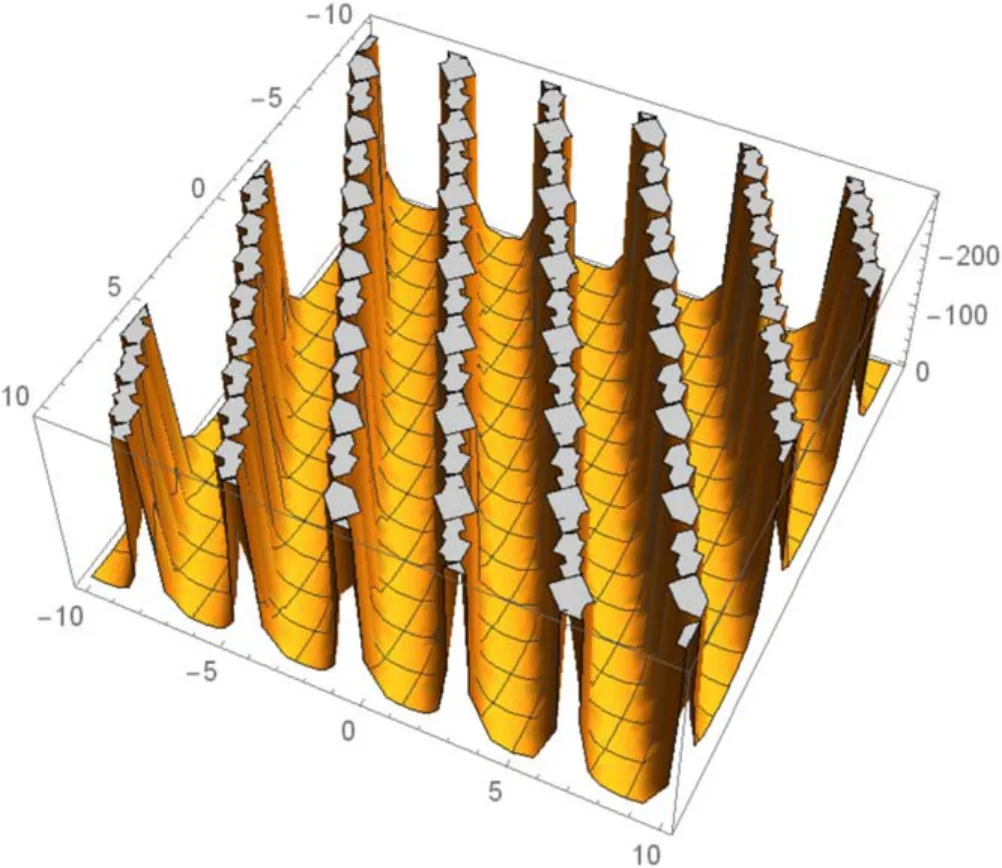
Figure 10.The 3D graph in equation (3.17) implying the singular periodic soliton for c =2, v0=1,n =1.

Figure 11.The contour graph in equation (3.17) for c =2,v0=1,n =1.
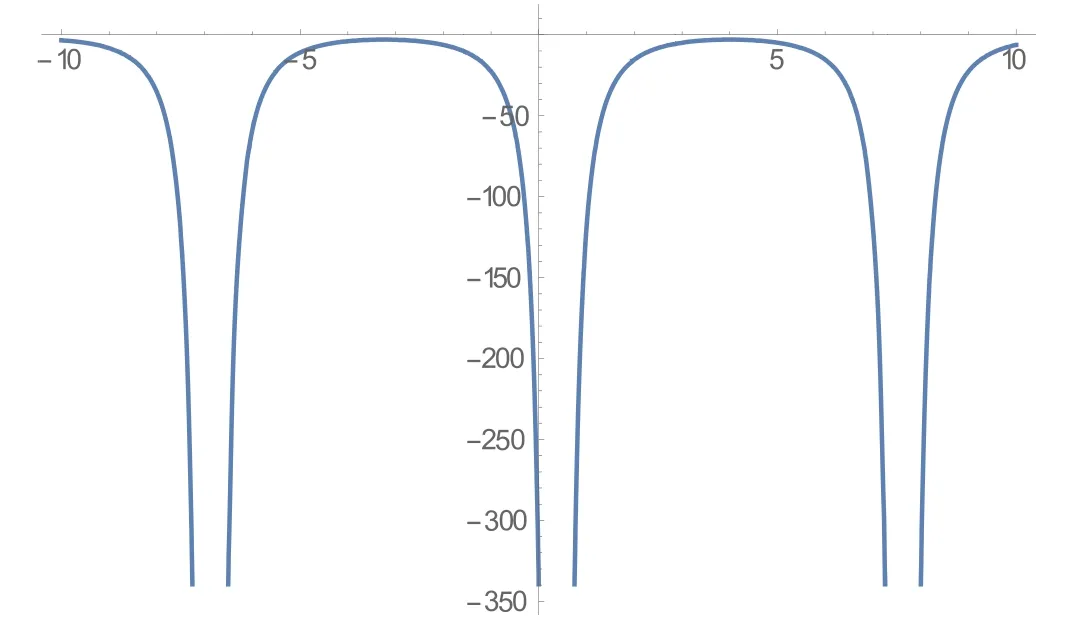
Figure 12.The 2D structure in equation (3.17) for c =2,v0=1,n=1,t=2.
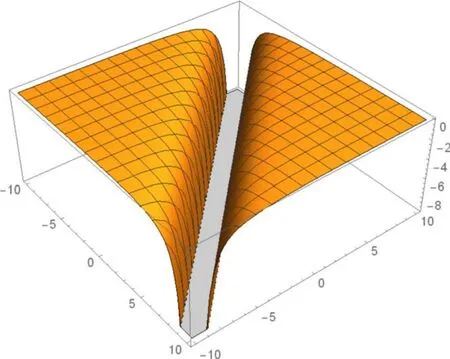
Figure 13.The 3D structure in equation(3.20)indicating the singular kink shape soliton for v0=1,n =2.
The current examination of the model discussed here confirms several new wave solutions and recovers some old results that existed in [51, 52].The results are expanded to highlight the distinctive dynamic properties of nonlinear waves in two-dimensional, three-dimensional, and contour diagrams by adjusting the parameters involved.Using the computer application ‘Mathematica’, the wave profiles were created, and their accuracy was verified by re-integrating the results into the initial governing model.
5.Conclusion
In this study,the unidirectional stochastic longitudinal wave equation in a MEE annular body has been solved by employing the dual(G'/G, 1/G)-expansion method.The solutions of this equation carry a momentous induction in multifarious scientific and engineering sectors such as the field of sensors and actuators.The exact solutions of the above proposed unidirectional partial differential equation refer to the three fundamental solutions which are trigonometric,hyperbolic,and rational function solutions and all of these fundamental solutions represent different types of solitary wave solutions in an electromagnetic potential field.The attained solitary wave solutions such as singular periodic solition and kink solition solutions are represented by three-dimensional, two-dimensional, and contour graphs.These obtained solutions can give a clear concept of many engineering and scientific phenomena spatially in electric and magnetic fields.Consequently, we mention that the presented expansion technique is efficient, transparent, and almost compatible with linear and nonlinear components.
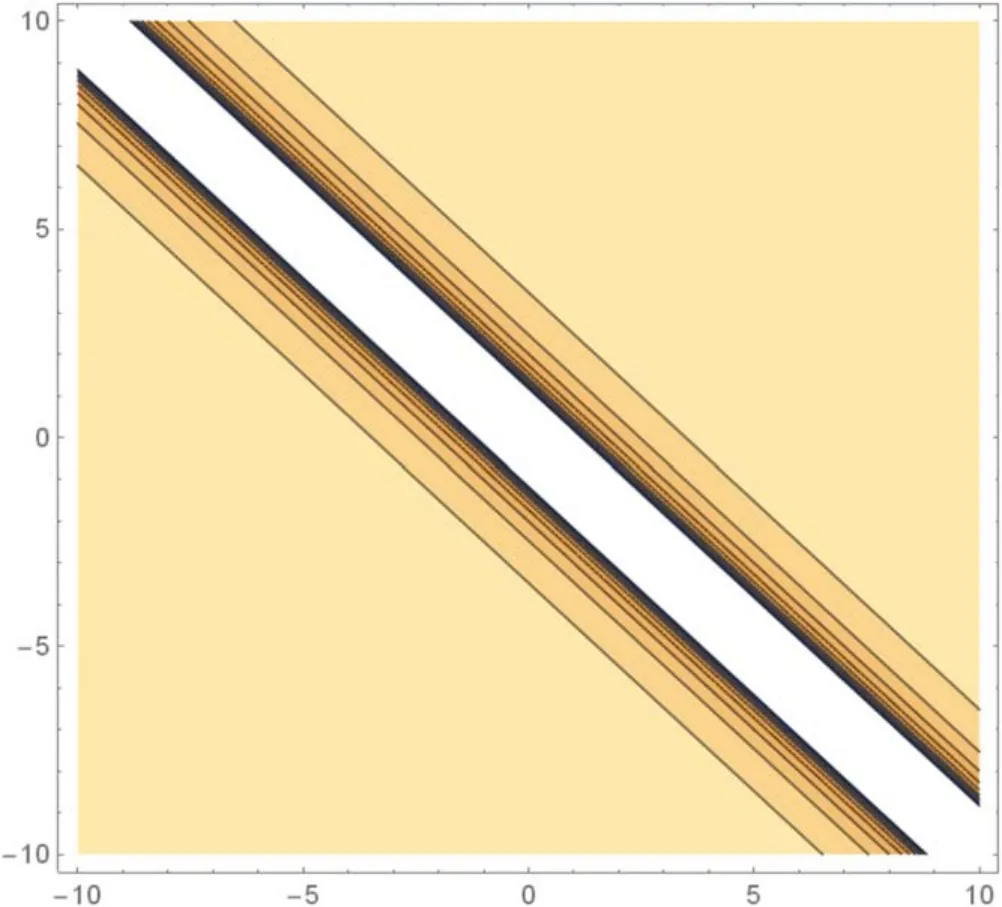
Figure 14.The contour figure in equation (3.20) for v0=1,n =2.
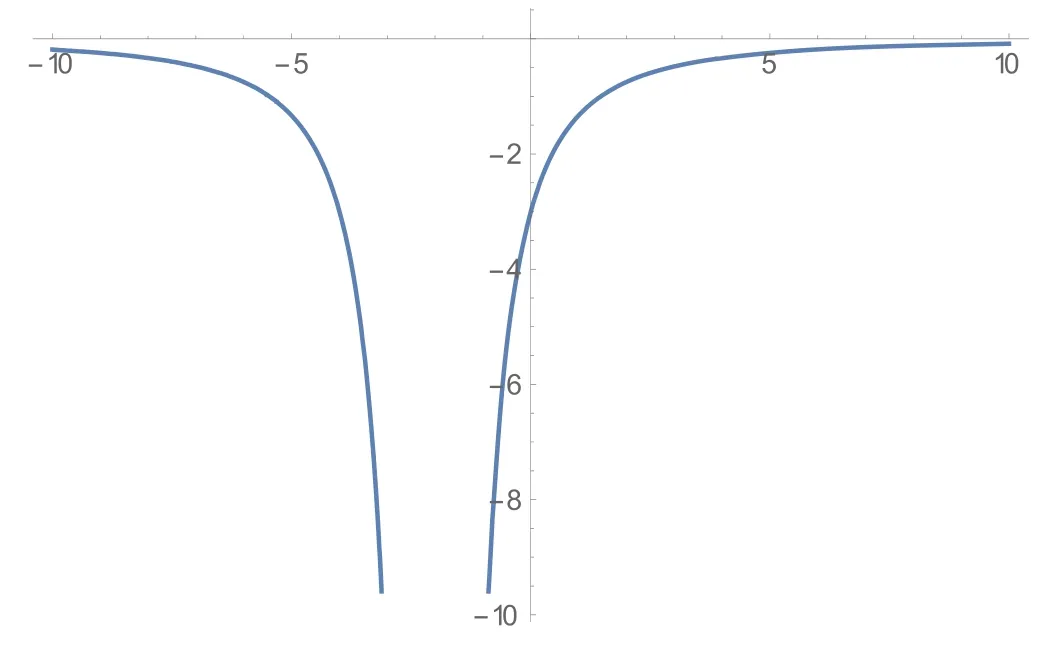
Figure 15.The 2D graph in equation(3.20)for v0=1,n =2, t =2.
ORCID iDs
 Communications in Theoretical Physics2023年8期
Communications in Theoretical Physics2023年8期
- Communications in Theoretical Physics的其它文章
- On the emergence of gravitational dynamics from tensor networks
- Ordered exponential and its features in Yang-Mills effective action
- Searching for a0(980)-meson parton distribution function
- Tsallis relative α entropy of coherence dynamics in Grover′s search algorithm
- Multiple soliton solutions and symmetry analysis of a nonlocal coupled KP system
- Painlevé analysis, infinite dimensional symmetry group and symmetry reductions for the (2+1)-dimensional Korteweg-de Vries-Sawada-Kotera-Ramani equation
