Painlevé analysis, infinite dimensional symmetry group and symmetry reductions for the (2+1)-dimensional Korteweg-de Vries-Sawada-Kotera-Ramani equation

Bo Ren, Ji Linand Wan-Li Wang

1 Department of Mathematics, Zhejiang University of Technology, Hangzhou 310014, China

2 Department of Physics, Zhejiang Normal University, Jinhua 321004, China

Abstract The (2+1)-dimensional Korteweg-de Vries-Sawada-Kotera-Ramani (KdVSKR) equation is studied by the singularity structure analysis.It is proven that it admits the Painlevé property.The Lie algebras which depend on three arbitrary functions of time t are obtained by the Lie point symmetry method.It is shown that the KdVSKR equation possesses an infinite-dimensional Kac-Moody-Virasoro symmetry algebra.By selecting first-order polynomials in t, a finitedimensional subalgebra of physical transformations is studied.The commutation relations of the subalgebra, which have been established by selecting the Laurent polynomials in t, are calculated.This symmetry constitutes a centerless Virasoro algebra which has been widely used in the field of physics.Meanwhile,the similarity reduction solutions of the model are studied by means of the Lie point symmetry theory.

Keywords: KdVSKR equation, Painlevé analysis, Lie point symmetry, Kac-Moody-Virasoro algebra

1.Introduction

Symmetry study has been widely studied in nonlinear science.The Lie group method plays an important role in seeking solutions of nonlinear partial differential equations (NLPEs)[1, 2].The special solutions of a given equation can be obtained in terms of solutions of lower dimensional equations[3].Compared with Lie point symmetry, many nonlocal symmetries and corresponding group invariant solutions are obtained by the Painlevé analysis and Lax pair [4-7].Lie point symmetries and the related Kac-Moody-Virasoro algebra of the Kadomtsev-Petviashvili equation have been constructed by using the standard classical Lie approach [8].The generalized symmetries and the generalizedW∞symmetry algebra are derived through the formal series symmetry approach [9-11].The generalizedW∞symmetry algebra will reduce to the Virasoro algebra with certain parameters[10].An isomorphic centerless Virasoro symmetry algebra is found in the (2+1)-dimensional and the (3+1)-dimensional integrable models [12-16].The formal series symmetry approach [9, 10] and the master symmetry approach[17,18]can be successfully applied to find infinitely many generalized symmetries.The related topics of symmetry have triggered interest in (2+1)-dimensional soliton systems.Naturally, an important problem is whether other (2+1)-dimensional systems possess the Kac-Moody-Virasoro algebra and the centerless Virasoro symmetry algebra.

Recently, a (2+1)-dimensional Korteweg-de Vries-Sawada-Kotera-Ramani (KdVSKR) equation is proposed to describe the resonances of solitons in shallow water [19,20].The (2+1)-dimensional KdVSKR equation reads as [19]

where α and β are arbitrary constants.The(2+1)-dimensional KdVSKR equation (1) reduces to the standard KdV equation and the (2+1)-dimensional SK equation with β=0 and α=0, respectively.The KdVSKR equation (1) possesses a rich physical meaning in nonlinear science.The standard KdV equation and the (2+1)-dimensional SK equation are completely integrable by means of the inverse scattering transform method [21].Soliton molecules and full symmetry groups of the (1+1)-dimensional KdVSKR equation are obtained by the Hirota bilinear and the symmetry group direct methods[22].The soliton molecules,the multi-breathers,and the interactions between the soliton molecule and breathers/lumps of (1) are explored by the velocity mechanism [20].

The purpose of this work is to study the integrable property and the symmetry group of the KdVSKR equation.The outline of the paper is arranged as follows.In section 2,the Painlevé property of the (2+1)-dimensional KdVSKR equation is studied by the standard singularity analysis.In section 3, the symmetry algebra and the infinite-dimensional symmetry group of the model are established by the Lie point symmetry.In section 4,some physical meanings of the finitedimensional algebras are obtained by restricting the arbitrary functions oftto first degree polynomials.By selecting the Laurent polynomials int, the commutation relations of the subalgebra are calculated.In section 5, the group invariant solutions are obtained by the corresponding symmetry reductions.The conclusions are discussed in section 6.

2.Painlevé analysis of the KdVSKR equation

The integrability of the NLPEs is studied by various methods.Among these methods,the standard Painlevé method,i.e.the Weiss-Tabor-Carnevale (WTC) method [23], is widely used to verify the integrable conditions of given NLPEs [23-25].In this section, we shall study the integrability of the (2+1)-dimensional KdVSKR equation (1) with the WTC method.

According to the WTC approach, the Painlevé test includes three steps:the leading order analysis,resonant point determination and resonance condition verification.While all the movable singularities of their solutions are only poles,the model is called the Painlevé integrable system.The fieldsuandware expanded about the singularity manifold φ(x,y,t)=0 as

whereujandwjare the arbitrary functions ofx,y,t.By the leading order analysis, the constants α1and α2are positive integers.The values of α1and α2read

and the functionsu0andw0are

The Laurent expansion of the solution in the neighbourhood of the singular manifold becomes

By substituting (5) into (1), the coefficients of (φj-7, φj-3)are

The values of the resonances are

The resonance atj=-1 represents the arbitrariness of the singularity manifold φ(x,y,t)=0.The functions ofu1andw1read asu1=2φxx,w1=2φxyby selecting the coefficients of(φ-6, φ-2).To verify the existence of arbitrary functions at other resonance values, we proceed with the coefficients of(φ-5, φ-1).The resonances atj=2, 2 represent the arbitrary functionsu1andw1.By collecting the coefficients of (φ-4,φ0), the functions ofu2andw2satisfy the relationw3φx-u3φy+w2x+u2y=0.Either of the functionsu3andw3is thus an arbitrary function.The functionsw4andw6are arbitrary at the resonancesj=6 andj=10, respectively.From the above analysis,the number of arbitrary functions is the same as the number of resonances and (1) passes the Painlevé test in the sense of the WTC method.

3.Lie point symmetry of the KdVSKR equation

Based on the Lie point symmetry method [1], the KdVSKR equation is invariance under transformation

where ∊is the infinitesimal parameter.The general vector field reads

whereT,X,Y,UandWare the functions oft,x,y,uandw.The symmetry equations for σuand σware expressed as a solution of the linearized system (1)

The corresponding symmetries of σuand σware

Over-determined equations of the KdVSKR system can be obtained by substituting (11) into the symmetry equations (10) and takinguandwto satisfy the KdVSKR system.Solving the over-determined equations leads to the infinitesimals

wheref(t),g(t)andh(t)are the arbitrary functions oftand the dots indicate derivatives with respect tot.The corresponding vector is

withP(f),Q(g) andR(h)

4.Symmetry group of KdVSKR equation

The commutation relations of the infinite-dimensional Lie algebra (14) are

It is shown that each term ofP(f),Q(g) andR(h) constitutes Kac-Moody-Virasoro type algebra.The subalgebra forP(f)is just the Virasoro symmetry algebra from (15).The KdVSKR system possesses the Virasoro symmetry structure.

Some physical symmetries of the KdVSKR equation can be obtained by restricting the arbitrary functionsf(t),g(t)andh(t) to be first-order polynomials int.By restricting the arbitrary functionsf(t),g(t) andh(t) to be first-order polynomials int, a finite-dimensional subalgebra of physical transformations can be obtained

whereM,LandKare generated translations in thet,yandx,respectively,Nis the generated dilations and a Galilei boost in thexdirection,Hhas some properties of a rotation and a Galilei boost in theydirection, andDyields a Galilei transformation in thexdirection.

By using the functionsf(t),g(t) andh(t) to be Laurent polynomials int, the subalgebra reads

withn∈Z.The commutation relations of this subalgebra are

The above symmetry constitutes a centerless Virasoro algebra which has been widely used in the field of physics [26].

5.Similarity reductions of KdVSKR equation

The Lie symmetries, a one-dimensional optimal system and symmetry reductions of the nonlinear systems are presented in a systematic review [27-29].The explicit solutions are obtained by solving the related characteristics equations.Based on the Lie group method,the group invariant solutions of the KdVSKR system can be obtained by solving the following characteristic equations

For the similarity group solutions, three cases are listed.

Case I.For the simplification form of the reduction system,we selectf(t)=1.The similarity solution is given by solving the characteristic equations

with the similarity variablesandThe group invariant functionsUandWsatisfy

If we get the solution of(25),the group invariant solution can be obtained by using (24).

Case II.The similarity solution is derived by solving out the characteristic equations withf(t)=0

withM=15βh(t)-(t), the symbolic functioncsgn(M),the similarity variableand the group invariant functionsUandW.Substituting (26) into (1)satisfies the following equations

Case III.With the casef(t)=0 andg(t)=0, the group invariable solution is

the solutionsU(y,t)andW(y,t)satisfy the reduction systems

By solving (29) and using (28), the solution of (1) is expressed as

The multi-breathers, the multi-lumps, and the interactions between the soliton molecule and breathers/lumps of (1) are studied by means of the Hirota bilinear method [19, 20].The dynamics for multi-soliton solutions, lump waves, and their interactions of the nonlinear systems are analyzed by the Hirota technique [30-32].The multi-solitary waves of the non-autonomous Zakharov-Kuznetsov equation are studied by utilizing Hirota’s bilinear method [33].Based on the Lie point symmetry method, the dynamical behaviors of the invariant solutions are discussed through three-and twodimensional profiles [27-29].Here one demonstrates the invariant solution graphically in case III.The constant β and arbitrary functionsh(t),B(t),C(t) are taken as

Figure 1 depicts the dynamical wave structures ofwin (30)and parameters as (31).The basic application of the trigonometric function on the timescale and the wave-propagation pattern of the wave alongtis periodic from figure 1.

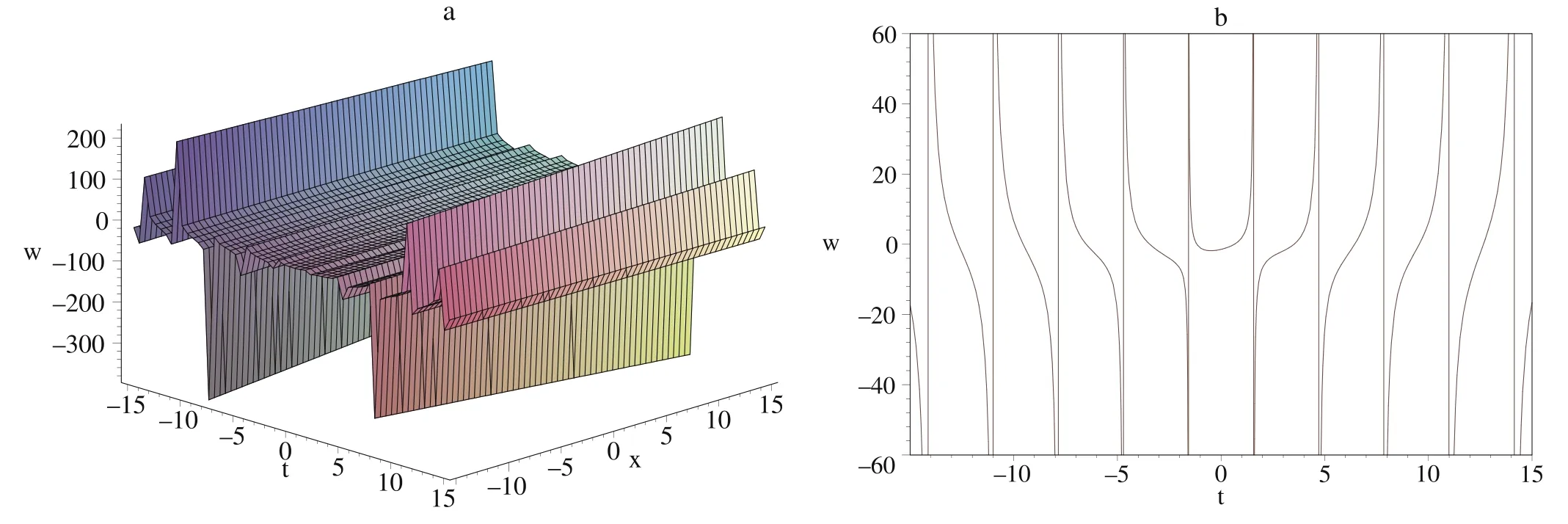
Figure 1.(a) The three-dimensional of the invariant solution at y=6.(b) The wave-propagation pattern of the wave along t axis at x=6 and y=6.

6.Summary and conclusion

In summary, the Painlevé analysis and the symmetry reductions of the (2+1)-dimensional KdVSKR equation are systematically studied.The Lie group of the KdVSKR equation is the transformations for acting on the independent variablesx,y,tand the dependent variablesu,w.The symmetry group of the KdVSKR equation is infinite-dimensional due to the existence of three arbitrary functions.The infinite-dimensional Lie groups and Lie algebras,in particular,Kac-Moody-Virasoro algebras are constructed by the Lie point symmetry method.A finite-dimensional subalgebra of physical transformations is studied by selecting first-order polynomials int.The commutation relations of the subalgebra,which are obtained by selecting the Laurent polynomials int, have been constructed.From the commutation relations, the symmetry constitutes a centerless Virasoro algebra.Furthermore, symmetry reductions are performed by using the Lie point symmetry method.Three types of similarity reduction equations are studied in the implementation of the method.The Lie point method has generated many reductions and exact solutions in a number of physically important NLPEs [34, 35].The study of symmetry reductions would be valuable help in work on the nonlinear fields.

Acknowledgments

This work is supported by the National Natural Science Foundation of China Grant Nos.11775146,11835011 and 12105243.