如何引导学生灵活选用不同方法取近似数
□许含英
在解决问题的过程中,如何引导学生根据实际情况灵活选用不同方法取近似数?可以采用以下教学活动。
一、解决实际问题,探索取近似数的方法
1.呈现实际问题,理解“进一法”
教师出示题目1,让学生独立思考解决问题。
题目1:妈妈要将2.5 千克香油分装在一些玻璃瓶里,每个瓶最多可装0.4 千克。需要准备几个瓶?
学生自主探索,汇报呈现不同方法。
方法①:2.5÷0.4=6.25(个),6.25≈6(个)。
方法②:2.5÷0.4=6.25(个),6+1=7(个)。
方法③:0.4×6=2.4(千克),2.5-2.4=0.1(千克),6+1=7(个)。
讨论:求需要几个瓶子,为什么不按照“四舍五入法”取6个?引导学生得出:6个瓶最多能装2.4千克,剩下0.1千克还需要1个瓶子,所以6+1=7(个)。
2.利用直观图式,理解“去尾法”
教师出示题目2,让学生独立思考解决问题。
题目2:王阿姨用一根25 米长的丝带包装礼盒。每包装一个礼盒要用1.5 米丝带,这根丝带可以包装多少个礼盒?
学生汇报呈现不同方法。
方法①:25÷1.5=16.6……≈17(个),可以包装17个。
方法②:25÷1.5=16.6……≈16(个),可以包装16个。
教师提问:你同意哪一种方法,为什么?引导学生得出:采用“四舍五入法”时,如果包装17个礼盒,1.5×17=25.5(米),25.5米>25米,丝带不够。
教师用课件出示图1、图2,让学生结合图式和算式说理。

图1
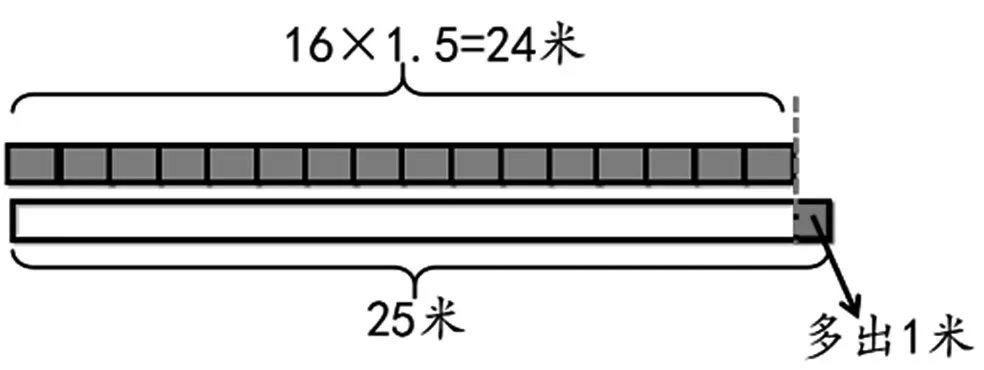
图2
在图1中,如果包装17个礼盒,需要25.5米,比25 米少了0.5 米。第17 个礼盒缺少0.5 米,所以只能取整数16。
在图2 中,1.5 米丝带包装1 个礼盒,包装了16个以后,一共用了24 米,还剩下1 米。1 米小于1.5米,不够再包装1个礼盒了,所以取整数16。
3.比较取近似数,归纳基本方法
教师引导学生思考:通过这两道题,你有什么发现?从而让学生明白:第1 题,求需要多少个瓶子,不管小数部分是多少,都要进一取整数,这种方法叫作“进一法”;第2 题,求丝带可以包装几个礼盒,不管小数部分是多少,都要舍去尾数取整数,这种方法叫作“去尾法”。在解决实际问题时,要根据实际情况取商的近似值。如“至少需要几个瓶子”“至少需要几个箱子”等问题,应采用“进一法”。如“一根丝带最多扎几个礼盒”“一瓶药最多够吃几天”“这些钱最多可以买多少本书”等问题,应采用“去尾法”。
二、迁移应用方法,根据实际情况灵活运用
1.迁移应用
(1)用170 米的布做儿童套装,每套用布2.3米,能做多少套?
(2)有170吨的煤,用载重2.3吨的一辆小车运输,需运输多少次?
(3)雨燕的飞行速度是170 千米/小时,蚊子的飞行速度大约是2.3 千米/小时。雨燕的飞行速度大约是蚊子的几倍?
2.比较异同
在解决实际问题时,教师要引导学生根据实际情况选用合理的方法:第(1)题要用“去尾法”,第(2)题用“进一法”,第(3)题可以根据保留小数位数用“四舍五入法”。
以上教学借助实际问题,帮助学生理解取近似数的方法,让学生通过辨析具体情境,体会如何运用“进一法”“去尾法”取近似数。

