基于干扰观测器的机械臂广义模型预测轨迹跟踪控制

卢紫超, 李 通, 孙泽文, 田 霖, 孙 亮, 刘冀伟

(1.北京科技大学 智能科学与技术学院,北京 100083; 2.中华人民共和国民政部一零一研究所,北京 100070;3.北京科技大学 自动化学院,北京 100083)

机械臂是高精度、多输入多输出、高度非线性、强耦合的复杂系统。因其独特的操作灵活性,已在工业装配、安全防爆等领域得到广泛应用。机械臂的非线性控制稳态精度和抗干扰能力一直是研究领域的重点问题。

在许多控制系统的设计过程中,常常会面临实际对象与数学建模得到的模型之间存在差异的问题,这是因为在建模过程中存在参数不确定性以及外界的未知干扰[1-4]。

广义预测控制(Generalized Predictive Control,GPC)算法是通过在线辨识获得模型参数,并利用模型参数实现多步预测和滚动优化,同时又具有自适应特征的控制算法。因此GPC对于建模误差等未知因素具有较好的适应能力。但是一些含有较大建模误差和较大外界干扰的复杂控制系统,会出现预测输出和实际输出相差较大的情况,无法得到满意的控制效果[5-9]。文献[10]将改进的比例性能指标型广义预测控制器引入多变量系统中,通过预测增量表征系统变化趋势,并通过控制量进行补偿优化控制性能。文献[11]提出了一种求解广义预测控制律的快速算法,解决了计算量较大的问题。文献[12]提出了一种模糊广义预测控制的方法,并将其应用到了连续搅拌反应釜系统中。

干扰状态观测器通过独立于数学模型的特殊反馈机制可以很好地跟踪参数不确定性和外界干扰,并成功应用于各种对象[13]。利用干扰观测器观测系统存在的不确定性成为了一种克服这些不确定性的有效算法[9]。将干扰观测器应用于GPC中,通过估计模型不确定性以及外界的干扰来提高系统的鲁棒性能。文献[14]提出了一种基于状态观测器的四旋翼反步输出反馈轨迹跟踪控制器,分数阶反馈的状态观测器可以提高控制器的跟踪性能和自适应性。文献[15]提出了基于状态观测器的有限时间控制器,解决了非仿射非线性系统的执行器故障问题。文献[16]针对刚性航天器的容错问题,设计了一种基于干扰观测器的自适应鲁棒控制器。文献[17]提出了一种基于扩张状态观测器和反步法的四旋翼飞行器姿态控制器,通过干扰观测器观测四旋翼飞行器收到的扰动,提高了系统的鲁棒性能。

本文将广义模型预测方法应用于机械臂轨迹跟踪控制器的设计之中,优化控制系统的性能。针对机械臂轨迹跟踪运动学子系统,采用GPC方法设计期望的虚拟关节角速度。对于机械臂轨迹跟踪动力学子系统,考虑机械臂的参数不确定性和未知外界扰动,利用广义预测控制方法设计关节力矩控制输入。从工程实际角度出发,考虑到机械臂运动的匹配和不匹配模型不确定性的影响以及机械臂在实际运行环境中外界的未知干扰,GPC可以通过多步预测和滚动优化对建模误差和未知因素产生较好的适应能力,本文基于非线性干扰观测器方法设计鲁棒控制项,保证系统的鲁棒性。基于上述设计思想,本文针对受外部干扰和参数不确定性影响的多输入多输出耦合机械臂系统动力学模型,提出了一种具有非线性干扰实时在线补偿的GPC方法。在控制设计中,针对关节角度子系统和关节角速度子系统的级联性,分层设计了基于非线性干扰观测器的广义模型预测运动学控制器和动力学控制器。所提出的控制方法可以为机械臂控制器提供一种通过预测时长整定控制器反馈增益的调参方法,整定后的参数可保证受控系统的误差轨迹和控制输入具有一定优化性能。通过数值仿真验证了闭环系统的稳定性和有效性。

1 问题描述

考虑n自由度机械臂的动力学模型如下:

(1)

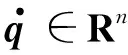
若考虑机械臂模型的参数不确定性及外部干扰影响,将机械臂动力学模型(1)降阶为2个级联的子系统,第1个子系统描述关节角位置动态:

(2)

第2个子系统描述关节角速度动态:

(3)

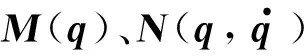
假设外部干扰信号f1、f2及其各阶导数均有界且期望关节运动轨迹qr(t)本身及其各阶时间导数均有界。

本文控制目标是考虑模型(2)和模型(3)中的外部不匹配干扰f1和聚合干扰f2的影响,设计控制输入力矩u使得机械臂关节轨迹q(t)跟踪上期望轨迹qr(t),并使得轨迹跟踪误差最终收敛到原点小邻域。

2 关节角位置跟踪控制器设计

(4)

取最小值。该性能指标函数对关节角位置和角速度跟踪信号进行了优化,保证系统动态跟踪性能。

由泰勒展开公式可得在t+τ时刻关节角位置q(t+τ)及其一阶导数的预测值可近似写为

(5)

(6)

(7)

(8)

由以上各式可将指标函数J1近似化成如下形式:

(9)

式中:A为3n×3n的常值对称矩阵。

(10)

(11)

(12)

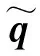
(13)

(14)

则y-yr可以表示为

(15)

则由式(9)有:

(16)

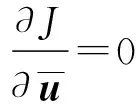
(17)

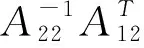
(18)

由Kp的定义可知:

(19)

则Kp为正对角阵。将式(13)和式(14)代入式(18)可得:

(20)

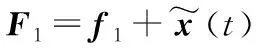
(21)

式中:z1为观测器状态;Lp为观测器的增益矩阵。可以设计实际的角速度虚拟控制律为

(22)

由式(19)可知,增益矩阵Kp的取值取决于预测时长T1。在实际的机械臂应用中,预测时长表示对未来状态的预测程度。当预测时长T1较大时,可以对关节角位置有较长的预测,但是会产生较大的误差,会降低轨迹跟踪的精度;当预测时长T1较小时,无法使式(4)中的滚动优化性能指标达到最优值。故在实际应用中选择一个合适的预测时长,使控制器可以根据当前误差及时修正系统的输入信号。观测器增益矩阵LP也需要根据实际应用对其进行调节,过大和过小都无法获得较好的预测效果。

3 关节角速度跟踪控制器设计

针对关节角速度子系统设计了实际关节力矩控制输入,设定合适的控制力矩实现最优跟踪。与关节角位置跟踪设计类似,通过最小化以下指标函数实现:

(23)

类似虚拟控制器设计的推导过程,可设计使得式(23)最小的广义预测控制器,得到控制力矩输入为

(24)

类似Kp的推导过程,可以得出角速度控制系统中的Kd为

(25)

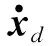
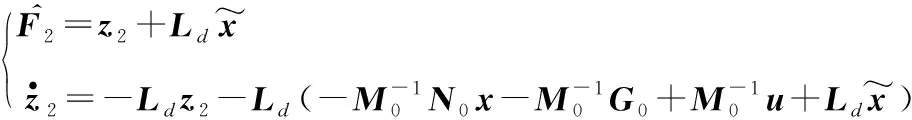
(26)

式中:z2为观测器状态;Ld为观测器的增益矩阵。输入的控制力矩可以重新设计为

(27)

式中:角速度控制系统中的Kd取决于预测时长T2和加权常数λ。Kd的取值过小会降低轨迹跟踪的跟踪精度,过大会产生较大的控制力矩。Ld参数的选取直接影响观测器的预测效果。所以针对不同的应用对象需要根据实际情况进行调节以实现良好的控制性能。

4 稳定性分析

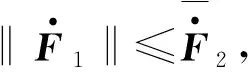
证明:定义观测器的误差为

(28)

(29)

由式(21)和式(26)可得出扰动观测器的误差为

(30)

(31)

定义李雅普诺夫函数:

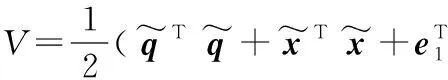
(32)

对李雅普诺夫函数求导得:

(33)

整理得:

=-ρV+c

(34)

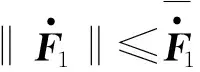
其中:

(35)

(36)

5 仿真算例

本文采用双连杆刚性机械臂进行了数值仿真,验证了所提出控制器的有效性。定义q=[q1,q2]T,x=[x1,x2]T分别为机械臂的关节角度和关节角速度。两连杆刚体机器人数学模型中的相关矩阵如下[8]:

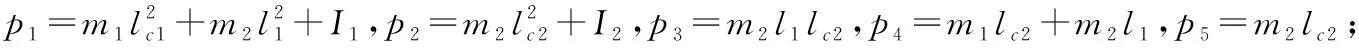
假设双联杆机械臂的初始角位置为q(0)=[0,0]T,采样周期τ=0.01 s,预测时长T1=1.3 s,T2=1.7 s,关节角期望轨迹qr=[0.1sin(0.5t)+cos(0.5t),0.1sin(t)+cos(t)]T,扰动力矩f=[0.5sin(0.1t)+0.5,0.5(cos(0.1t))+0.5]TN·m,不匹配外部干扰f1=[0.1sin(0.1t),0.1sin(0.1t)] N·m,扰动观测器的初始状态z1(0)=z2(0)=[0,0]T,观测器增益矩阵Lp=25E2,Ld=5En,M0中的标称参数m10=1.5 kg,m20=0.5 kg,l10=0.34 m,l20=0.3 m。PD控制器中,比例系数kp=100E2,微分系数kd=10E2。经过数值仿真,实验结果如图1～图3所示。

图1 关节1的角位置和角速度跟踪误差

图2 关节2的角位置和角速度跟踪误差

图3 关节1和关节2的控制输入

由图1～图3可以看出,在本文提出的控制器(27)的作用下,关节1和关节2的角位置跟踪误差在0.5 s时到达期望值附近,随后实现稳定跟踪。关节1和关节2的角速度跟踪误差在0.6 s收敛至零附近,并保持在零的领域中实现稳定跟踪。在初始阶段,为了实现较快的跟踪,控制输入在初始阶段较大,在0.5 s后渐渐收敛至零附近。干扰观测器的观测值如图4和图5所示,最终收敛至零的邻域。相对于经典的PD控制器,本文所提出的控制器在收敛时间和跟踪精度方面均表现比较优异,在关节1中,明显看出本文提出的控制器具有较小的超调。相对于经典的广义预测控制器,加上干扰观测器后,系统的收敛精度和收敛速度明显优化。此外,通过绝对误差积分准则(Integral Absolute Error,IAE)和时间乘绝对误差积分准则(Integral of Time and Absolute Error,ITAE)对3种控制方法进行了对比,结果如表1所示,控制器(27)的控制效果明显优于其他两种控制方法。综上所述,基于干扰观测器的广义模型预测控制器可以使角位置误差和角速度误差收敛至零的邻域,实现较好的跟踪效果。

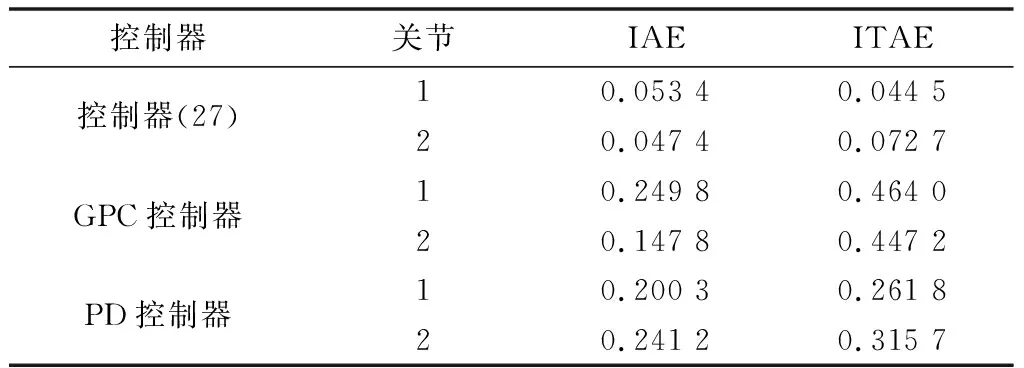
表1 3种控制器IAE、ITAE指标对比

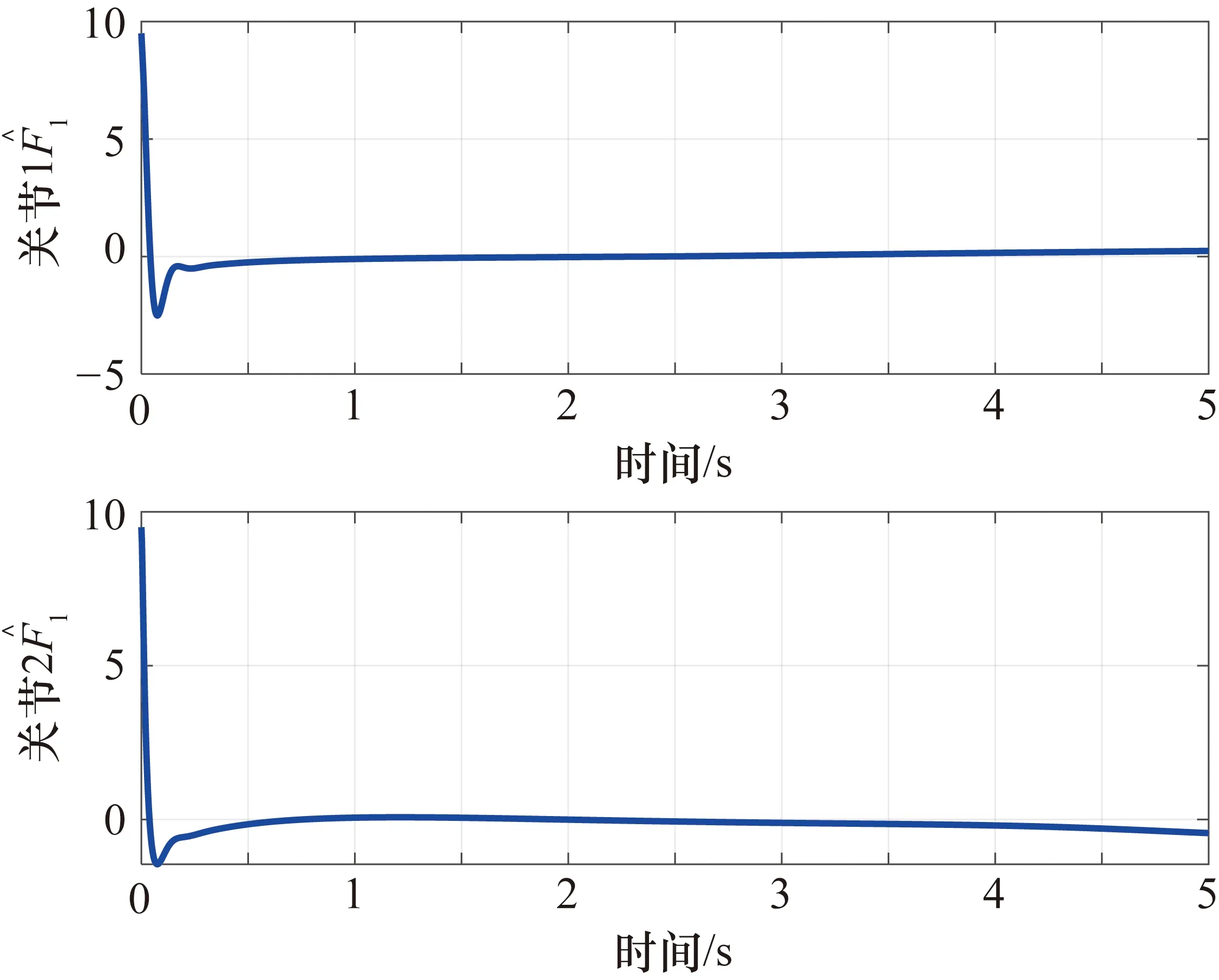
图4 关节1和关节2的值

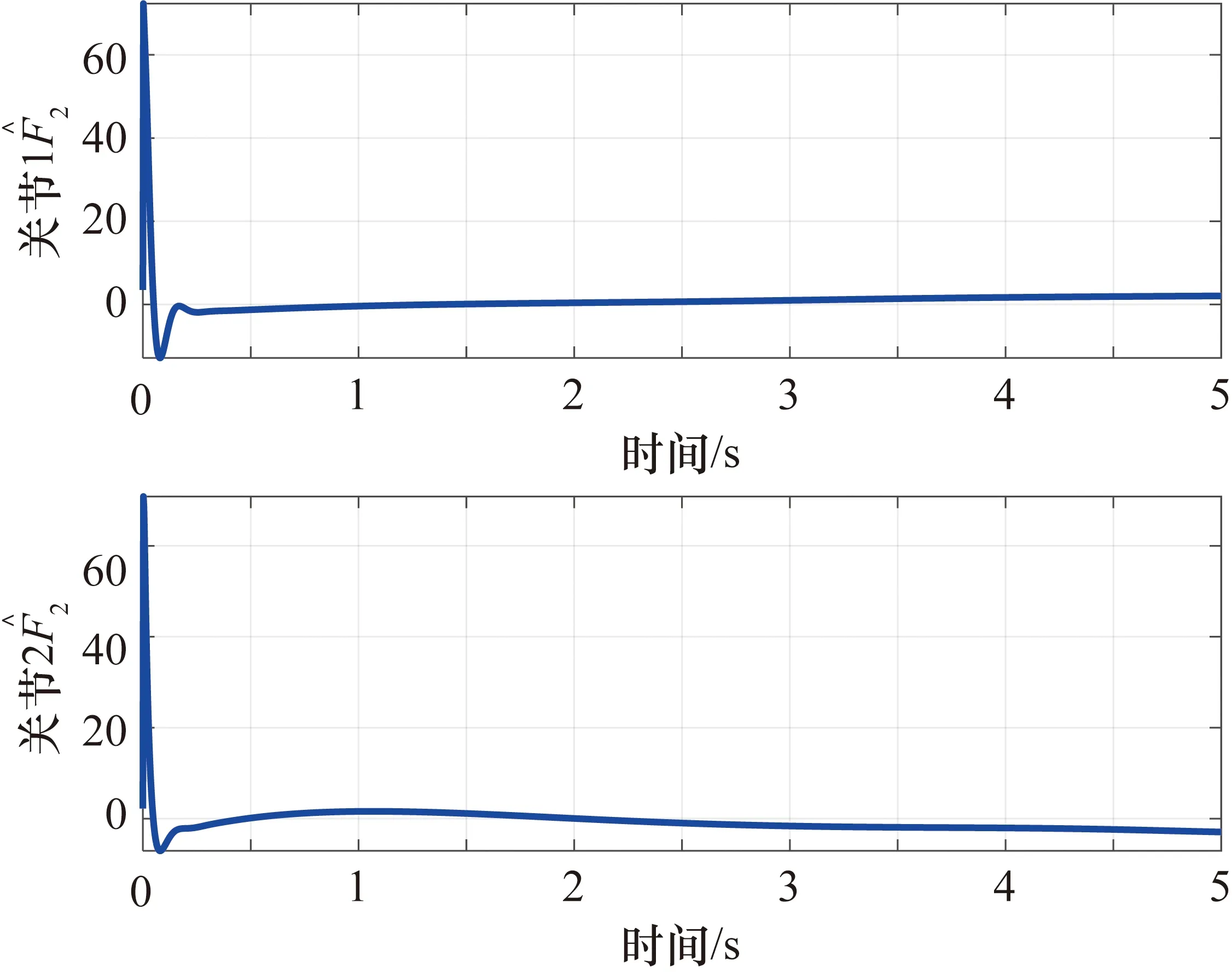
图5 关节1和关节2的值

为了验证本文所提出控制方案的鲁棒性,在各种数字信号干扰和负载变化(复合干扰)情况下进行了仿真实验。将外部干扰重新取为f=[C1sign(sin(0.4πt)),C2sign(sin(0.4πt))],其中C1分别取6、4、2;C2分别取3、2、1。在机械臂的末端执行器上添加变化负载m=1.25+sin(t)。仿真实验结果如图6～图9所示。从图6～图9中可以看出,在复合干扰的作用下,当数字干扰信号到达时,关节1和关节2的角位置误差和角速度误差会产生波动,并且干扰的幅值越大,波动越大。在控制器(27)的作用下,在受到干扰后,角位置跟踪误差和角速度跟踪误差会收敛至零的邻域,实现稳定的跟踪效果。

图6 不同复合干扰下关节1的角位置跟踪误差

图7 不同复合干扰下关节1的角速度跟踪误差

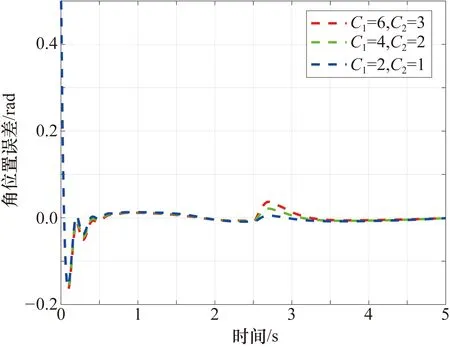
图8 不同复合干扰下关节2的角位置跟踪误差

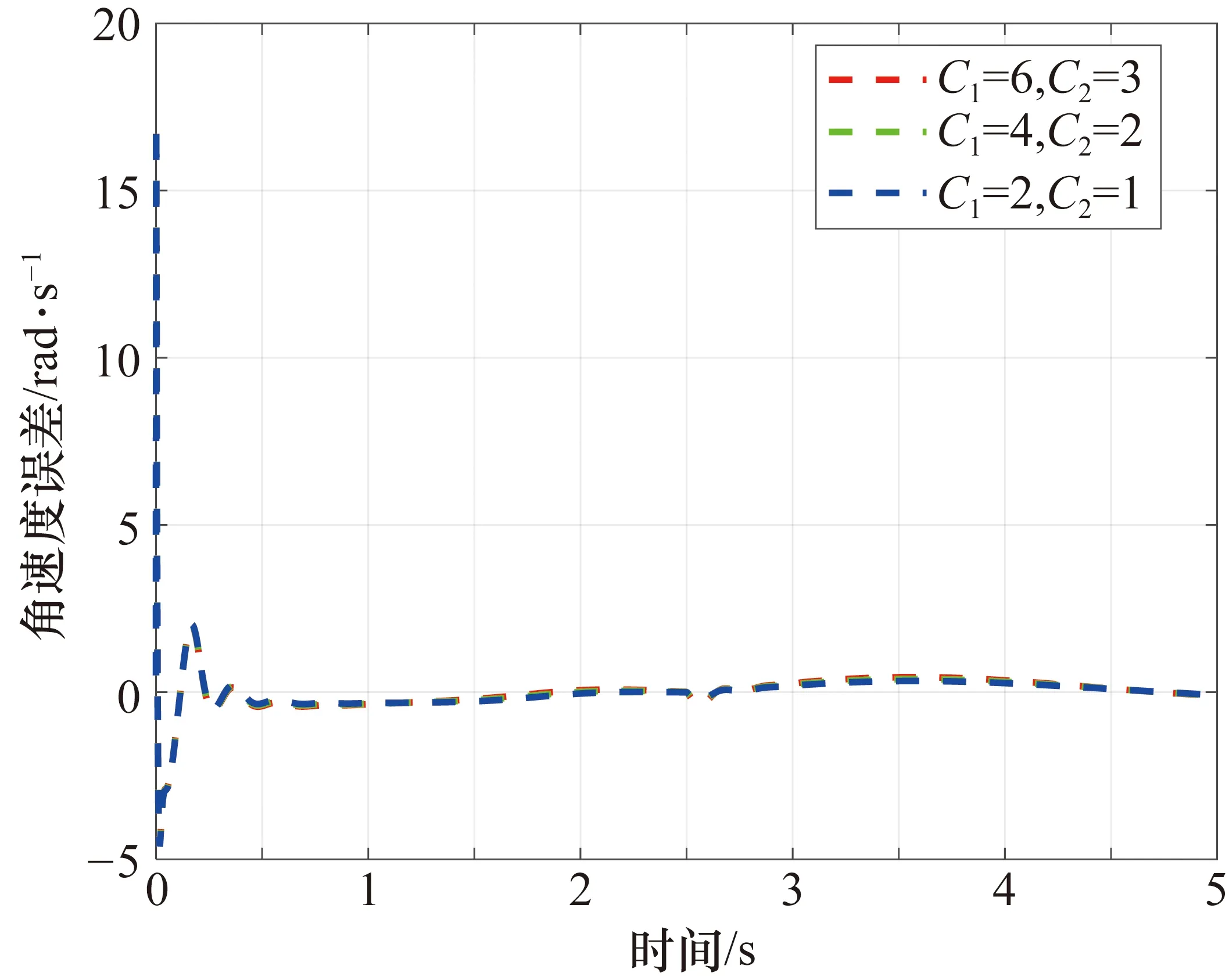
图9 不同复合干扰下关节2的角速度跟踪误差

6 结束语

本文以两连杆刚性机械臂为例,进行了基于干扰观测器的广义模型预测轨迹跟踪控制研究。利用GPC的方法分别设计了期望的虚拟关节角速度和关节力矩控制输入,利用非线性干扰观测器的方法实时估计并补偿系统模型中的不确定性。由于GPC可以通过多步预测滚动优化来适应实际的工作场景,并 通过干扰观测器补偿建模的不确定性和外界干扰,故通过调节合适的参数可使本算法应用于不同的实际工程。仿真结果表明,所提出的控制器可以使跟踪误差收敛至零的邻域,实现很好的跟踪效果。本文为了验证所提出控制器的鲁棒性,进行了数字信号干扰和负载变化共存情况下的仿真实验,结果表明该控制器有较好的鲁棒性。