四参数二元Mc Kay型伽马分布的几何性质

万文龙,罗洁,许皓

(西华师范大学数学与信息学院,四川 南充 637009)

1 引言

信息几何是用微分流形或用黎曼流形来研究概率分布的学科,该学科的主要思想是亚马里(Amari)和永冈(Nagaoka)[1]提出的以费歇尔信息矩阵作为黎曼度量来建立黎曼流形,而概率分布的全体参数被视为该流形的坐标系统[2]。统计流形是信息几何的核心内容,被证明具有由费歇尔信息矩阵给出的唯一黎曼度量和对偶仿射联络。

伽马分布是统计学的连续概率函数[3],是概率统计中非常重要的分布,许多分布都直接或间接地与之相关。麦凯拉(Mc Kay)和斯科(SC)[4]提出了二元Mc Kay型伽马分布,本文基于四参数二元Mc Kay型伽马分布,在其尺度参数和形态参数的基础上增添了位置参数[5－22]。为了更好地研究四参数二元Mc Kay型伽马分布的实际应用和其他统计性质,本文尝试从信息几何的角度研究其几何性质。

本文计算了四参数二元Mc Kay型伽马流形的信息矩阵及其逆矩阵、克里斯托弗符号和黎曼曲率张量,并给出了子流形的黎曼几何结构等。

2 统计流形

统计流形M＝的α－联络由下式给出:

其中g＝＜,＞是以ξ为局部坐标系的费歇尔信息矩阵,并且α－联络系数由下式给出:

当α＝0时,上式为黎曼联络系数。此外,统计流形的黎曼曲率张量由下式给出:

定义2.1 设(U;xi) 是M的一个局部坐标系,则其曲率张量的分量为:

Ricci曲率张量的分量为:

从而有数量曲率R为:

以及截面曲率K(u,v)为:

3 四维伽马流形的几何结构

若二元变量(X,Y)服从四参数二元Mckay型伽马分布,其联合密度函数为:

其中,β≤x＜y,a＞0,p＞2,q＞0,β是位置参数,伽马函数为:

关于X和Y的边缘密度函数分别为:

X与Y的协方差与相关系数为:

相关系数ρ随p,q变化的图像如图1所示。

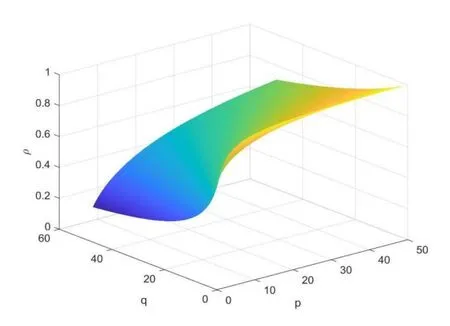
图1 相关系数随p 和q 的变化图

定理3.1 统计模型

是一个四维统计流形,称为四维二元Mc Kay型伽马流形,其自然坐标系为ξ＝(a,p,q,β)。

定理3.2 在自然坐标系ξ＝(a,p,q,β)下,四维二元Mc Kay型伽马流形的费歇尔信息矩阵G( ξ )为:

其中ψ(p)＝Γ′(p)/Γ(p) ,Γ′(p) 是伽马函数的导数。

证明根据其似然函数:

则有:

从而有:

证毕。

由上面结果可知费歇尔信息矩阵的行列式为:

其图像如图2所示,可以看到,随着p和q的增大,极速减小,其极限值为0。

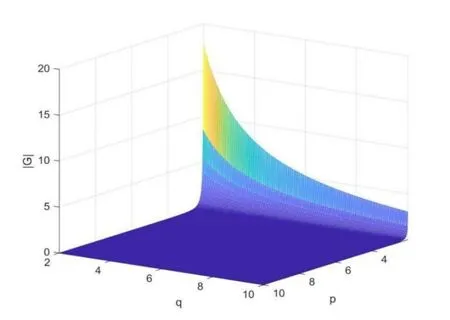
图2 行列式随p 和q 的变化图

通过计算可以得到费歇尔信息矩阵G (ξ)的逆矩阵G－1(ξ) ,其分量如下:

由(1)式,四维二元Mc Kay型伽马流形的黎曼联络系数分别为:

其余未列出的分量为0。

定理3.3 在自然坐标系ξ＝(a,p,q,β)下,流形M的曲率张量的分量由下式给出:

4 Mc Kay型伽马4－流形的子流形

4.1 子流形M 1 M:a＝1

在(3)式中,取a＝1,则有:

定理4.1在自然坐标系ξ＝(p,q,β)下,统计流形M1的费歇尔信息矩阵[gij]和它的逆矩阵[gij]分别如下:

定理4.2 在自然坐标系ξ＝(p,q,β)下,统计流形M1的黎曼联络系数分别为:

其余未列出的分量均为0。

4.2 子流形M 2 M:p ＝3

当p＝3时,统计模型

是一个三维流形,其自然坐标系为ξ＝(a,q,β)。

定理4.3 在自然坐标系ξ＝(a,q,β)下,统计流形M2的费歇尔信息矩阵[gij]和它的逆矩阵[gij]分别如下:

定理4.4 在自然坐标系ξ＝(a,q,β)下,统计流形M2的黎曼联络系数分别为:

4.3 子流形M 3 M:q＝1

当q＝1时,统计模型

是一个三维流形,其自然坐标系为ξ＝(a,p,β)。

定理4.5 在自然坐标系ξ＝(a,p,β)下,M3的费歇尔信息矩阵[gij]和它的逆矩阵[gij]如下:

定理4.6 在自然坐标系ξ＝(a,p,β)下,M3的克里斯托费尔符号如下:

4.4 子流形M 4 M:β＝0

当β＝0时,统计模型

是一个三维流形,其自然坐标系为ξ＝(a,p,q)。

定理4.7 在自然坐标系ξ＝(a,p,q)下,统计流形M4的费歇尔信息矩阵[gij]和它的逆矩阵[gij]如下:

定理4.8 在自然坐标系ξ＝(a,p,q)下,统计流形M4的黎曼联络系数分别为:

定理4.9 在自然坐标系ξ＝(a,p,q)下,统计流形M4的曲率张量分量为

5 总结

本文给出了基于信息几何的四参数二元Mc Kay型伽马流形,并计算了相关几何结构,包括费歇尔信息度量、黎曼联络和曲率张量等。此外,本文还给出了四参数二元Mc Kay型伽马流形的四个子流形的相关几何结构。二元伽马分布在地震预测和水文学上有广泛的应用,通过对其几何结构的研究,可以在相关概率预测模型上做优化与改进。