高中化学速率与平衡试题的解题技巧

李 蓉

(湖南省沅江市第一中学,湖南 沅江 413100)

化学作为高中阶段的一门重要学科,在高考化学中,化学速率与平衡有着很大的分值比重.对于化学速率与平衡试题来说,涉及到的知识内容比较多,解题难度大,要求学生具备较高的解题能力.因此,在高中化学解题教学中,对速率与平衡试题深入分析,帮助学生寻找解题思路,掌握题目解题方法,强化学生化学解题能力.

1 利用极端思维方式,完成化学试题解题

高中化学速率与平衡题目中,主要研究的是可逆反应,由于可逆反应不能够进行到底,借助逆向思维方式,利用极限法解题,完成求解.因此,在速率与平衡试题解题训练中,教师需要根据题目条件,引入极限分析思维,准确寻找解题切入点,帮助学生准确解题[1].

例1某个密闭容器中,温度恒定,进行如下反应:

一氧化碳和水蒸气各1 mol,在容器内反应到平衡,通过测量二氧化碳是0.6 mol,之后再加入3 mol的水蒸气,达到平衡之后,二氧化碳的体积分数可能是( ).

A.20% B.22.2% C.17% D.11.1%

解析根据题目条件分析,在原混合物中,二氧化碳与氢气的量均为0.6 mol,一氧化碳与水蒸气均是0.4 mol,达到平衡后,再次加入3 mol的水蒸气,平衡向反应正方向移动,一氧化碳转化率增加,二氧化碳体积分数增加,但是无法确定二氧化碳体积分数的具体数值.教师可以利用极限法分析题目,即一氧化碳转化率增大的极限为100%,最小的极限值则是零,结合化学平衡进行计算,根据两种极端状态,求解出二氧化碳的体积分析,即20%与12%,根据求解中的结果,在再次平衡之后,二氧化碳的体积分数应当处于两个极限值之间,因此,正确答案是C.

在此题解答中,教师鼓励学生利用极端分析思维,通过计算,寻找解题突破点,利用一氧化碳的最大极限和最小极限转化率,对二氧化碳体积分数进行计算,找出数值的大概取值范围,判断得出准确答案.

2 采取粗略估算方式,快速解答化学问题

高中化学解题中,一些速率与平衡试题,虽然可以利用公式进行计算,得出准确的答案,但计算的过程比较复杂,教师可以根据题目的特殊性,不采取计算的方式解题.在速率与平衡试题解答中,让学生根据平衡移动方向与结果,分析数量关系,采取粗略估算的方式,快速找出问题答案,简化计算步骤,提高学生解题效率.

A.6 B.5 C.4 D.3

解析在此题解题中,如果利用化学平衡进行计算,计算步骤复杂,很容易出现错误.因此,教师要求学生认真审题,从中找出关键信息,通过粗略估算解题.在具体的解题中,根据题意,知道化学反应是在恒温恒压的环境中进行的,可以从正反应的方向构建化学平衡,在平衡之后,由于容器体积增大,说明在恒温恒压下,容器内的气体总物质的量增加,所以不等式的2+n>4+3,求解得出n>5,符合题意的是A选项.

在此题解题中,改变以往化学平衡的计算模式,避免复杂的计算过程,使得解题错误,引入粗略计算的方式,准确找出题目中n的取值范围,结合题目选项,找出准确的答案,让学生快速准确解题.

3 利用平均分割思维,保证解题准确性

在解题过程中,速率与平衡题目具有特殊性,此类试题题型较多,但考查的方向基本相同.对于此类题目,对不同的起始状态加入同一种物质,在初始量是倍数关系时,利用平均分割的方式,将量多的变成若干少量的,通过这样等同平衡,明确问题解答思路,完成题目的结算[2].

解析通过审题可知,密闭容器并没有对容积、压强进行要求,需要结合题目中的条件进行分类讨论:(1)假设密闭容器恒压,第二次加入气体的物质的量是第一次的两倍,则容器容积也是两倍,对第二次的容器进行平均分割,分割为第一个容器容积相同的两个容器,求解出Z的物质的量的是1 mol×2=2 mol.(2)假设密闭容器的容积恒定,容器可以看做是恒压的,以此作为基础,采取加压方式使其体积变成原来的体积,在加压状态下,反向朝着正方向移动,求解出Z的物质的量大于2 mol.

在此类试题解题中,教师需要引导学生灵活利用平均分割思维,对题目情况分类讨论,之后对密闭容器适当的分割,使得解题思路更加清晰、简单,简化解题过程中的计算,采取平均分割法,计算出答案.

4 采取先拐先平方法,提高解题有效性

在不少的速率与平衡试题中,有着一些曲线图像,图像中有着拐点,如浓度与时间图像中,通过对拐点的先后分析,对其压强、温度进行分析,先出现拐点的曲线,意味着先到达平衡状态,通过这样的分析,根据变化找出规律,即压强、温度高,则浓度大.因此,教师需要让学生灵活利用先拐先平的方法,快速分析解题,得出问题的最终答案[3].

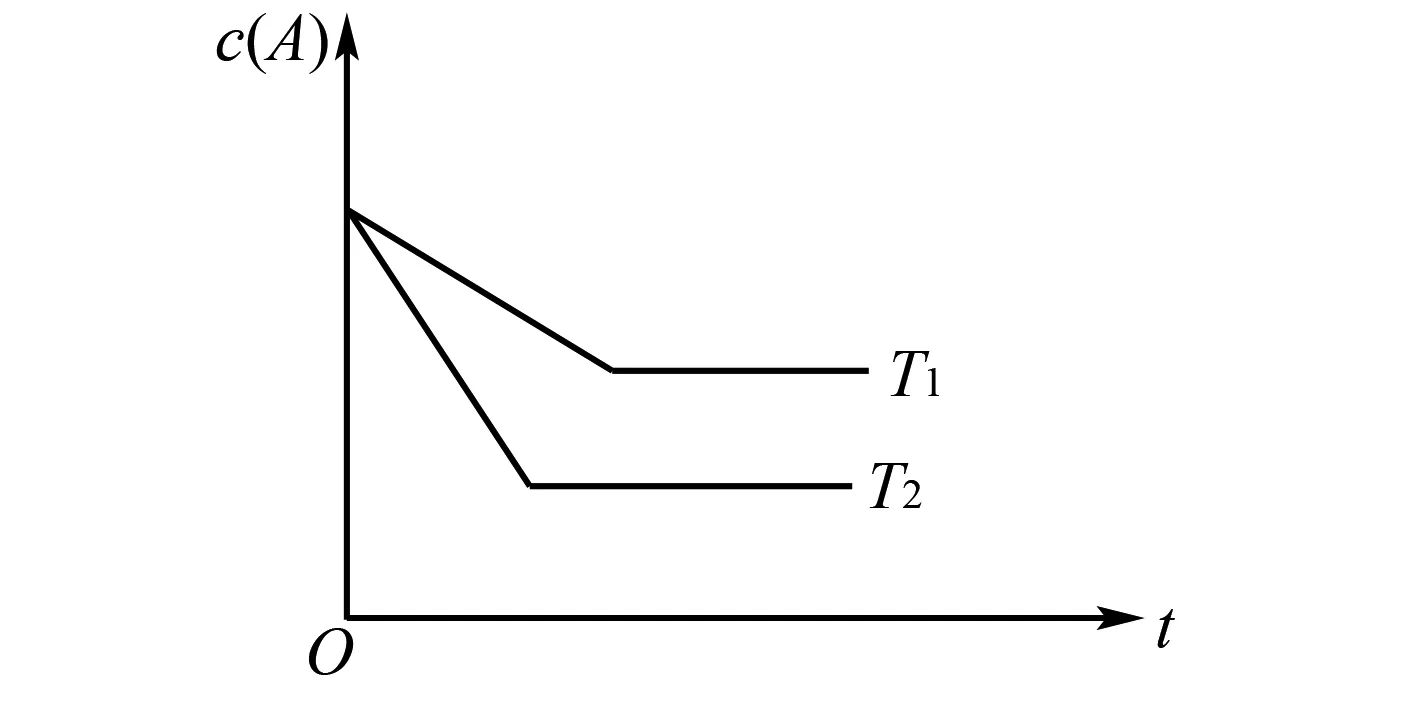
图1 化学反应浓度与时间关系图

解析在实际的解题中,让学生认真阅读题目,分析图中的曲线,拐点位置标示刚刚达到平衡状态.因此,根据图像分析,T2达到平衡状态时,所用的时间比T1少,则表明T2的速率大于T1的,因此,T2的温度比T1的高,由于温度越高,c(A)越小,所以得出此化学反应的正反应是吸热反应,温度上升,K持续增长,所以可以得出反应的温度T1小于T2,平衡常数K(T1)小于K(T2).

在此题解答中,教师引导学生利用先拐先平的方式,对图像进行分析,准确提炼题目信息,合理推理和判断,省略复杂繁琐的计算过程,帮助学生准确地解题.

5 利用等效模式,有效解答试题

在高考化学考试中,经常从新的情境和角度出题,所考查的知识内容与能力并没有变化.因此,在速率与平衡试题中,教师可以引入等效模型,结合题目信息,找出解题突破点,有效解答化学试题.

A.a大于bB.a等于b

C.无法比较 D.a小于b

解析通过对题目分析可以得知,想要解答题目,采取等效假设的方式,构建等效模型解题.在第一次达到平衡状态之后,再次充入2 mol的SO3,此时的平衡移动方式是正反应方向,物质的量的不断增加,如二氧化硫、三氧化硫以及氧气等.想要对两次平衡中二氧化硫的体积分数大小进行比较,难度比较大,因此,可以采取等效假设的方式,即V2 mol的SO3(旧平衡)等效2V4 mol的SO3(平衡三),压缩V4 mol的SO3(平衡四)等效V4 mol的SO3(新平衡).通过这样的方式,对平衡三与平衡四进行对比,压缩容器使得平衡方向向逆反应反向移动,可以得出a大于b,因此,正确答案是A.

在解题中,对于新旧平衡关系难以直接对比的题目,通过等效转化,构建等效模型的方式解答.在解题中,通过假设,构建与旧平衡等效的平衡,之后,通过增大体积转化成与新平衡等效的平衡模型,根据其中的数量关系,得出正确答案.

高中化学速率与平衡试题解题中,主要的考点是平衡状态的判断、平衡移动方向的判断以及平衡移动结果分析等.在实际的解题过程中,需要根据题目类型,灵活利用解题方式,有效解答速率与平衡试题.在解题训练中,要求学生不断地归纳和总结,掌握更多的解答方式,加强学生解题能力训练,提高学生考试成绩.