核心素养视域下数学命题课的教学研究
夏玉梅


摘 要:数学命题教学是学生学习和教师教学的重难点,也是发展学生数学核心素养的重要教学载体.研究从数学命题教学的现状出发,提出基于核心素养数学命题课的设计原则,在此基础上以“一元二次方程根与系数的关系”为支点,展示核心素养视域下命题教学的实践探索.
关键词:数学核心素养;数学命题教学;根与系数的关系
课程目标是数学课程育人价值的集中体现,《义务教育数学课程标准(2022年版)》(以下简称《标准》)将“会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界”确定为数学课程的育人指向,即数学核心素养[1].回顾近年来关于核心素养的研究,较多指向理论研究,且关于教学策略的研究也以说理为主,研究操作性不强.命题教学作为培养和发展学生核心素养的优质载体,往往容易被教育工作者所忽视.研究基于核心素养提出数学命题课的设计思想,以苏科版“一元二次方程根与系数的关系”这一具体案例为支点,尝试探究出数学核心素养在数学命题课的落脚点、生长点和发展点.
1 基于核心素养的数学命题课的设计思想
1.1 基于认知,理解数学核心素养
《标准》指出初中数学核心素养主要表现为抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识、创新意识[1].实际上,中学教师并不缺乏核心素养的理论知识,也熟悉数学核心素养的定义,但对其内涵的理解还不够深入,这不利于教师将数学核心素养内化为设计教学的依据.近年来,众多教育研究者就数学核心素养提出了自己的见解,如有研究者在整合数学核心素养相关研究的基础上,认为数学核心素养是个体从数学的角度观察事物,并借助数学知识与思想方法解决数学学习或者现实生活情境中相关问题的综合能力以及个体所持有的数学情感态度、价值观等[2].教师不应该故步自封,应尝试领略教育研究者的学术争鸣,结合自身的认知及教育经验,深入理解数学核心素养的内涵,逐步形成自己独到的见解.
1.2 研读教材,明确数学核心素养
数学核心素养的形成不是一蹴而就的,它往往以数学知识为依托,在学生的数学学习过程中慢慢生长.教师作为数学教材与学生之间的传话者,开发出教材中涵盖的数学核心素养对进一步在教学中培养学生的数学核心素养起着举足轻重的作用.
数学命题学习主要是学习数学中的公理、定理、公式、法则等内容,学习内容比较抽象,教师对命题教学中蕴含的数学核心素养的挖掘也普遍出现难点.实际上,一个单元或一堂课,不可能只涉及一个数学核心素养,逻辑推理和数学运算几乎在所有的数学课中都有体现[3].教师应以教育研究者研究教材的视角看问题,在此基础上学习优秀教师如何挖掘命题课中的数学核心素养,尝试以高观点的视角审视、反思自己的挖掘情况,从而明确教材中核心素养的体现之处.
1.3 合理设计,落实数学核心素养
数学命题教学相较于数学概念而言,往往更具抽象性、逻辑性.传统的命题教学往往是灌输式的,部分教师在教学中普遍会出现“直接给出数学命题,再让学生反复练习即可”的情况,这有碍于学生数学核心素养的生成.数学命题的教学设计要力求凸显本节课的核心法则、典型思维,教师应努力践行在教学中培养学生的数学核心素养.一方面,教师可以以多个优秀教师的教学设计为学习对象,尝试以他人的视角审视、反思自己的教学设计,初步设计出能培养学生数学核心素养的教学过程;另一方面,教师可以根据学生的层次,设计恰当的情境作为学生命题学习的载体,让他们亲身去经历命题的发现、探索过程,在课堂中真正落实数学核心素养.
为了让核心素养视域下的命题教学更具实践性,研究以“一元二次方程根与系数的关系”为支点,结合设计思想分析该课的教学背景,在此基础上再进行教学案例设计.
2 教学背景分析
在课程准备阶段,教师应根据学生的原有基础,结合课程蕴含的数学核心素养,明晰学生应达到的素养目标层次.
2.1 素养分析
苏科版教材从问题情境入手,通过让学生观察具体方程及相应根的关系,结合适当的提示语,鼓励学生提出猜想,培养学生的数学抽象能力,进一步引导学生证明猜想,锻炼学生的推理与运算能力,最后在适当时机提供针对性的例题,帮助学生强化知识.
2.2 学生诊断分析
本课的教学对象是初中三年级学生,他们较好地储备了用多种方法解一元二次方程等数学知识,了解了由特殊到一般的思想方法.该阶段的学生更偏向于从直观、形象的角度认识事物,虽然他们可能有一定的学习基础和推理兴趣,但更关注问题应用.
2.3 素养目标分析
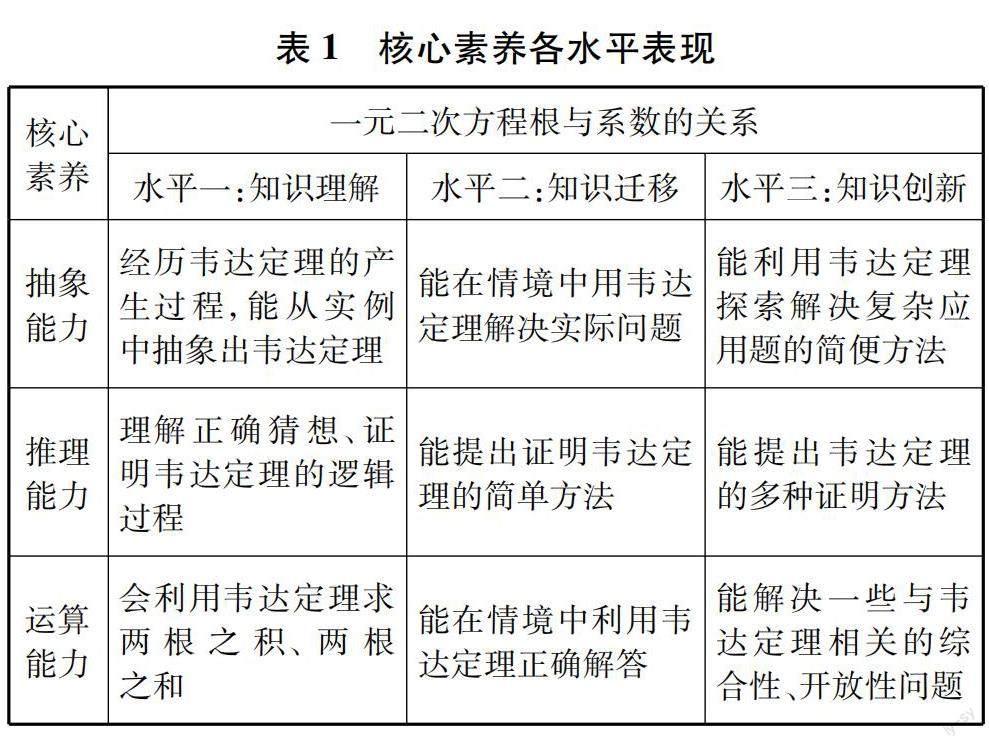
借助喻平教授关于核心素养的评价框架[3],确定该节课的数学核心素养达成的各水平表现,具体如表1所示.
在实际教学中,教师可以基于学生的原有水平,确定学生所应达到的数学核心素养目标层次,再根据目标逆向设计教学过程.
3 教学案例设计
本节课是一节数学命题课,设计思路主要采用问题解决模式,即以“问题情境—引入命题—命题证明—命题应用”为主线建构教学,在实现数学核心素养落地课堂的同时,也力求还原命题该有的“味道”.
环节1 知识回顾,导入新知
問题1:前面我们已经学习了如何求一元二次方程的根,回顾一下有哪些方法呢?
问题2:对于ax2+bx+c=0(a≠0),当判别式大于等于0时,你能说出一元二次方程的求根公式吗?求根公式揭示了一元二次方程的两根与系数间的直接关系,那么一元二次方程的根与系数间是否还有更深一层的联系呢?这就是本节课我们要继续研究的问题——一元二次方程的根与系数的关系.
设计意图:通过开放性问题1帮助学生复习旧知,让不同层次的学生均能够参与其中,同时也为本节课的探索之路做预热练习.根据学生的回答,教师进行引导、跟进提出问题2.利用问题2让学生明白前后所学知识有必然联系,但是没有告诉学生是怎样的联系,激发学生的探究兴趣,同时引出本节课要研究的内容.
环节2 合作探究,探索新知
小组合作 将学生分为A,B,C,D,E五个组,让其按顺序分别对应完成下面5个方程的求解,见表2.
问题3:观察表2,你能发现方程的根与系数之间有什么关系吗?(若学生找不出关系,教师则展示整理后的数据表,见表3)
设计意图:当学生不能注意到根与系数的关系时,教师给予适当暗示,帮助学生建立最近发展区.此外,教师故意将这五个方程的二次项系数均设置为1,1作为分母时通常会省略,容易导致学生得出:“两根之积与常数项相等,两根之和与一次项系数互为相反数”这样的错误猜想,教师顺势提出问题4,提醒学生注意根与系数的关系与方程的二次项系数相关.
问题4:利用得出的猜想,尝试验证之前提出的猜想是否正确?(注意可以关注之前没有涉及到二次项系数.)
⑥ 2x2-5x-3=0;
⑦ 3x2-7x+4=0.
设计意图:方程①~⑤得出的错误猜想,在方程⑥和⑦中被推翻.在这个过程中,让学生明白进行猜想时不能只参考特殊的例子,应该聚焦于更一般的例子,培养学生会猜想、能合理猜想的能力,进而发展学生的教学抽象能力.
几何画板演示:教师用几何画板演示更多案例(见图1),让学生从最直观的角度验证猜想的合理性.随着一元二次方程各项系数的改变,根与系数的关系都满足猜想.
素养培养:教师将课堂交给学生,以小组合作的方式,使学生发现规律、描述规律,经历从特殊到一般的学习过程,进而获得思维的碰撞、能力的提升、情感的交流、思维的延伸,逐步培养学生的抽象能力、推理能力.
环节3 验证猜想,得出定理
问题5:既然有了猜想,就需要验证猜想的正确性.我们由求根公式发现了根与系数之间存在着联系,你能从这个角度来证明猜想吗?
素养培养:教师引导学生证明猜想,帮助学生养成严谨的数学态度,培养学生的推理论证及运算能力.同时在证明时,指导学生从不同视角理解、分析、解决同一问题,发散了学生的思维.最后再借助课下思考题培养学生独立思考的能力.
环节4 例题讲解,强化新知
例1 若x1、x2是下列方程的两根.尝试不解方程,求出两根之和与两根之积.
(1) x2+2x-5=0;
(2) 2x2+x=1.
反思:想一想:求出两根之和以及两根之积的关键是什么?
例2 若方程2x2-mx-9=0的一个根为-3,求另一根及m的值.(教师可以适当提示学生,如图2)
例3 小明、小华、小亮分别求出了方程9x2+6x-1=0的根,请判断谁的答案正确?
设计意图:例1例3帮助学生巩固了一元二次方程根与系数的关系,考查了学生灵活运用知识解决问题的能力,让学生体会根与系数的关系在解题中的巧妙运用.在解题时也让学生注意到利用韦达定理之前,需要先将方程转化为一般形式,以便找准系数,熟练公式的结构,为后面解决难度系数较高的题目打实根基.
环节5 师生互动,课堂小结
总结1 本节课,我们学习了哪些内容?教师展示图3.
总结2 我们是如何研究本节课的知识的?教师展示图4.
设计意图:总结1让学生在互动中归纳总结、理顺知识,进一步突出了学习内容的重难点,帮助学生构建知识网络,培养他们优良的数学思维品质、数学学习习惯.总结2通过流程图让学生领悟知识点涵盖的思想方法,渗透由特殊到一般的认识事物的规律.
环节6 课后阅读,拓展延伸
课外阅读:公元前1800~1600年的古巴比伦时期,数学泥板上就记载关于给定两数的和与积,求两数的问题;三国时期,赵爽(约公元182~250)在研究勾股弦三边互求的方法中,也提到已知两数的和与积,分别求两个数.16世纪,意大利数学家卡丹(1501~1576)、法国数学家佩勒蒂耶(1517~1582)、意大利數学家邦贝利(1526~1572)均发现方程的根与系数之间存在联系.1591年,法国数学家韦达(1540~1603)正式以定理的形式给出方程的根与系数的关系.1629年,荷兰数学家吉拉尔将定理推广到一元n次方程,并对正根、负根、虚数根以及重根都成立,且发现幂和公式.
设计意图:了解韦达定理的历史发展过程,使学生领略数学的精髓,激发学生的学习兴趣,启发学生的认知发展,提高学生对知识的理解和对数学价值的认识.
4 结束语
核心素养指向课程的育人目标,它强调培养人的正确价值观、必备品格和关键能力.研究对核心素养视域下数学命题的教学提出相应的设计思想,并在此基础上以“一元二次方程根与系数的关系”为例进行具体分析,为教师提供了可操性强、目标指向明确的教学设计依据.新课程理念下,如何将课程目标落实到具体教学、让核心素养的培养生根落地并转化为课堂教学行动力,还需要更多的实践探讨.
参考文献:
[1] 中华人民共和国教育部,义务教育数学课程标准[M].北京:北京师范大学出版社,2022.
[2] 吕世虎,吴振英.数学核心素养的内涵及其体系构建[J].课程.教材.教法,2017,37(9):1217.
[3] 喻平.数学核心素养评价的一个框架[J].数学教育学报,2017,26(2):1923+59.

