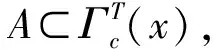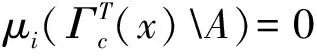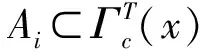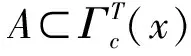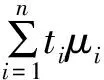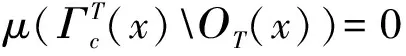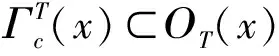群作用的测度可扩性

金秋实,董美花

(延边大学理学院,吉林 延吉 133002)

1 引言与基本概念

Utz[1]在二十世纪中期引入了可扩同胚的概念:如果存在常数ε>0,使得对于所有的x∈X,n∈,都有成立,则称紧致度量空间上的同胚f:X→X是可扩的,其中

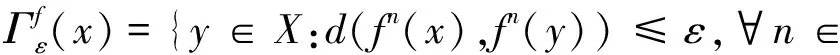
M*(X)={μ∈M(X)|μ是非原子的}

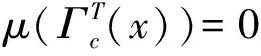
定义1.2设N∈,如果存在c>0,使得对于所有的x∈X,都有中不超过N个元素,则称T∈Act(G,X)是N-可扩的。如果存在c>0,使得对于所有的x∈X,都有是可数的,则称T∈Act(G,X)是可数可扩的。

2 群作用的N-可扩测度和扩大测度

定理2.1对于所有的T∈Act(G,X),下面的陈述是等价的:

1)T是可数可扩的;

2)T是测度可扩的。

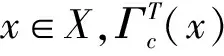
得出矛盾,故T∈Act(G,X)是可数可扩当且仅当其是测度可扩。

注2.2测度可扩与度量的选取无关,即假设T∈Act(G,X)在度量d2下是测度可扩的,蕴含着T在度量d1下仍是测度可扩的,其中d1和d2等价。

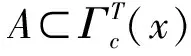
本文并不要求这个定义中的测度是不变的和非原子的。

定理2.4紧致度量空间上的连续作用是N-可扩当且仅当每一个Borel概率测度是N-可扩。

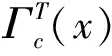
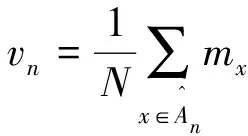
其中mx表示在x上支持的Dirac测度。事实上,

2)如果Bn∈β(X),n>0,对任意的i≠j,有Bi∩Bj≠∅成立,则得到

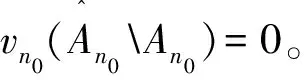
关于一个给定测度的N-可扩常数,有一个简单的备注。

注2.5如果c是Borel概率测度的N-可扩常数,则对于每一个0

定理2.6设T是一个度量空间X上的连续作用,N∈+。如果μ1,…,μn是X上的Borel测度且t1,…,tn>0,t1+…+tn=1,则有

成立。由此可见

即

推论2.7设T是一个度量空间X上的连续作用,则Borel测度μ1,…,μn的有限凸组合是1-可扩的当且仅当对于任意的i=1,…,n,μi是1-可扩的。

引理2.9设T是一个度量空间X上的连续作用,x∈X,则mx是1-可扩的当且仅当x是可扩点。

(1)

成立。现假设mx是1-可扩的,可扩常数为c,则对任意的y∈X,都有

由此可知

{y∈X:mx({y})≠0}={x}

引理2.9和推论2.7可以得到以下推论:

推论2.10设T是一个度量空间X上的连续作用,则Dirac测度的有限凸组合是1-可扩的当且仅当它是在可扩点上被支持的。

定理2.13连续作用T∈Act(G,X)是测度扩大的当且仅当它是几何可扩的。

证明假设T∈Act(G,X)是测度扩大的,但是不是几何可扩的。于是对于每一个n∈,都存在xn∈X使得取一个点定义测度μ∈M(X)为

设c>0为T的测度扩大常数,并选择n∈,且由于

得出矛盾,故T∈Act(G,X)是几何可扩的,反之显然成立。