ITIC:一种高效的k-影响社区top-r查询算法
谭玉婷 王习特 白 梅 周虹宇 朱 斌
(大连海事大学信息科学技术学院 辽宁 大连 116000)
0 引 言
现实世界中的诸多网络,如生物网络、社交网络等,都包含社区结构。发现网络中的社区是网络科学中的一个基本问题,近年来受到研究者们的广泛关注[1-5]。网络中的社区结构数量通常较多,在许多实际应用领域中,人们往往只对在网络中影响力较大的社区感兴趣[5]。受此启发,在文献[5-6,14]中基于k-core的概念提出并研究了网络中社区影响值排名的top-r查询问题。k-影响社区是网络中联系密切(即满足k-core属性)、具有较大影响且不存在包含关系的子网络。本文用k-core模型来模拟社区结构的凝聚性[1,5,11-13,15],因此社区即为k-core,并且社区影响值是k-core中所有节点权重的最小值。根据k-core的概念,满足k-core且影响值较大的社区可表示为“k-influential Community”,本文中用缩写k-IC表示。如图1所示的网络,其中包含13个节点{v1,v2,…,v13},每个节点的权重表示其影响值的大小。若取k=3,网络中包含两个k-IC:{v10,v11,v12,v13}和{v1,v2,v3},其社区影响值分别为13和12。

图1 k-影响社区示例
目前,关于k-IC查询问题已经取得了大量优秀的研究成果,但是现有工作大部分关注的是结构的凝聚性,而忽略了节点的属性[7-9],比如影响力。针对这些问题,提出了网络中k-IC的top-r查询问题。这一问题在许多领域有重要的应用,例如从电商直播平台形成的社交网络中识别出由粉丝数量高的主播形成的k-IC,这些主播的影响力都很大,通过他们的推荐,产品的销售量会提高很多。同时,k-IC的非包含属性能减少节点间的重复,因此可识别到更多有影响力的主播。此外,还可用来从生物网络中提取骨架结构[7],以及识别数据库研究人员协作网络中最具影响力的k-IC来组织研讨会[5]等。
本文主要针对网络中k-IC的top-r查询问题,提出了一种新型的k-IC查询算法。目前对此问题的相关研究主要有文献[5-6,14]。其中文献[5-6]中提出了直接算法和基于索引的算法。直接算法基于给定图的k-core分解计算社区,算法中逐步删除属性值小的节点,运行最大连通组件(MCC)算法发现下一个k-IC,然而文中对于是否具有包含关系的判断没有给出高效的方法。基于索引的算法首先建立索引,然后根据给定的r和k,提取前r个位于索引树的叶子节点的k-core。虽然基于索引的算法相较于直接算法更有效,但是构建索引的时间消耗大且该索引结构需要的空间与原始图形的大小基本相同,消耗内存也较大。直接算法中最耗时的是识别图中包含最小权重节点的连通分量,鉴于此,文献[14]提出了Forward算法,仅对最后的k次迭代进行连通分量的计算,但是该算法依然是从权重较小的节点开始处理,需要对整个网络进行处理最后才能得到结果。针对这些问题,本文提出了一种新型的算法,该算法不需要频繁地计算图中的连通分量以及判断k-core间的包含性,并且从权重较大的节点开始处理,只对网络中的部分节点进行处理即可渐进且快速求得前r个k-IC。
本文设计了一种表状索引结构对网络图进行管理和维护,并提出了有效解决k-IC的top-r查询的新算法。具体地,本文贡献总结如下:
(1) 提出了W-D(Weight-Degree)索引结构,用于管理各个节点的度数及其具体的邻居节点,并根据权重大小对节点进行排序。使用该索引可以确定被取节点的顺序,并对度数不满足参数k的节点进行过滤,同时可以加快节点之间邻居关系的判断,提高了k-IC的查询处理效率。
(2) 提出了k-IC的top-r查询优化算法ITIC。该算法从权重较大的节点开始处理,无须处理大多数权重较小的节点,并且不需要频繁地计算图中的连通分量;另外,算法渐进输出k-IC,当k-IC的数量满足用户的需求时,用户可以在任何时间终止算法。
(3) 进行了详细的性能评价实验。实验结果表明本文所提出的k-IC的top-r查询优化算法ITIC可以有效地处理k-IC的top-r查询问题。
1 相关工作
本节主要对k-IC查询的相关研究进行概述。与本文所研究问题最为接近的有文献[5-6,10,14]。
Li等[5-6]将网络建模为无向图G=(V,E),其中G中每个节点的权重表示其影响力。针对此模型,提出了DFS算法,用于在线搜索影响值较大的前k个社区,在线搜索算法迭代地应用以下三个子程序:(1) 将当前图形删减为满足γ-core的最大子图;(2) 识别出最大子图中包含最小权重节点的连通分量,这是下一个γ-影响社区;(3) 从图中删除最小权重节点。最后的k个影响值较大的γ-影响社区就是结果。该算法需要多次迭代和多次进行复杂的连通分量计算,效率较低,并且算法从权重最小的节点开始计算,逐步删除权重小的节点,在计算结束时才能得到top-k个γ-影响社区。对于非常大的图,基于DFS的算法比较低效,所以Li等设计了ICP-Index索引结构,用于预先计算k-core,但是构建索引所需的内存与原始图形的大小基本相同,消耗内存较大。
Chen等[14]改进了文献[5]中的在线搜索算法,提出了Forward和Backward两种在线算法。Forward算法仅对最后的k次迭代进行连通分量计算,但依然是从权重小的节点开始计算。Backward算法虽然是从权重大的节点开始处理,但是算法中多次调用updateCores更新节点的核数,使得算法的时间复杂度很高。Bi等[10]对在线搜索算法进行了改进,提出了局部搜索算法,但是算法通过多次迭代增大的方式确定子图,计算成本不低且存在不确定性,并且该算法没有给出高效的判断k-core间是否具有包含性的方法。
总之,目前现有的k-IC的top-r查询算法存在诸多不足,无法保证计算效率,因此本文就此问题进行了研究。
2 问题描述
本文主要研究如何高效地计算出网络中的前r个k-IC。为了描述方便,表1中给出了本文的符号定义。然后给出了k-IC及相关内容的形式化定义。
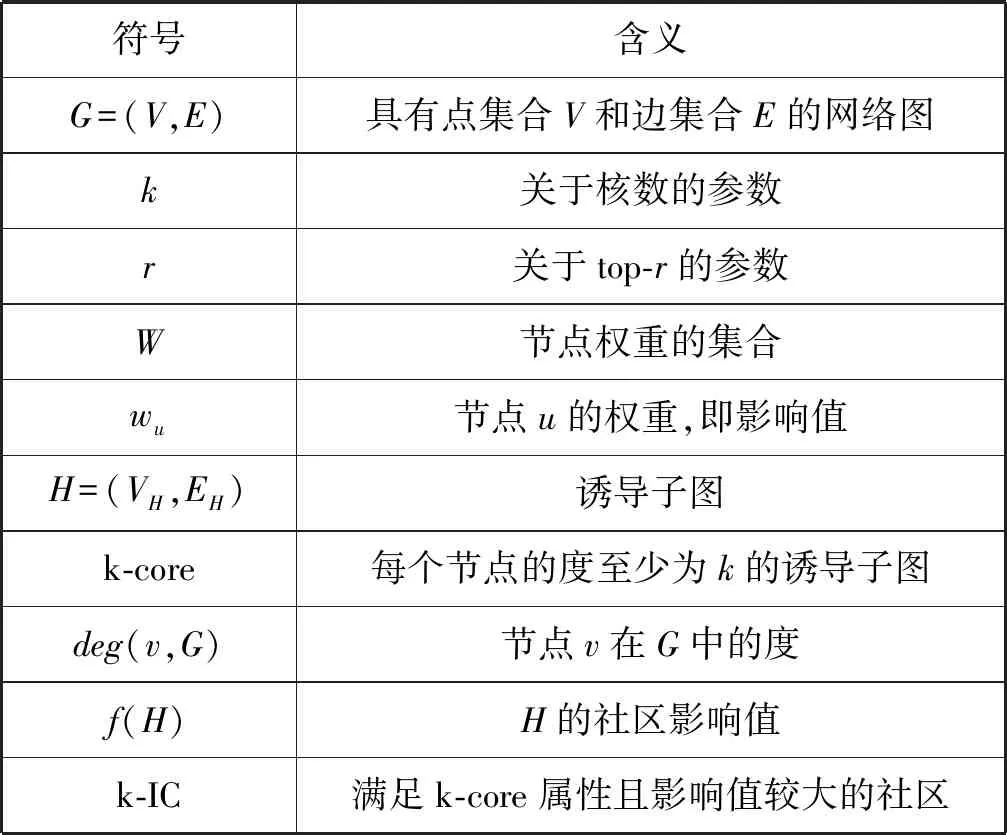
表1 符号表示
把网络建模为无向图G=(V,E),其中V和E分别表示点集合和边集合。G中的每个节点u都具有权重wu∈W(例如PageRank或其他用户定义的属性),表示u的影响值(或重要性)。在本文中,假设不同节点的权重不同,即wv≠wu,v≠u。
文中的deg(v,G)表示节点v在图G中的度数。设H=(VH,EH)为G=(V,E)的诱导子图,即VHV,EH={(u,v)|u,v∈VH,(u,v)∈E}。如从图1中选取节点v1、v2、v3、v4,形成的G的诱导子图如图2(a)所示,保留了在图1中与v1、v2、v3、v4有关的所有边。若去掉此诱导子图中的任意边,如去掉v1、v4之间的边,形成的图仅为G的子图,不再是诱导子图,如图2(b)所示。若H是诱导子图,且其中每个节点v∈H的度数至少为k,即deg(v,H)≥k,则H称为k-core。若H′是k-core,并且没有更大的k-core可以包含H′,则H′称为最大k-core。

(a) 诱导子图 (b) 子图
定义1社区影响值[5]。给定无向图G=(V,E)和G的诱导子图H=(VH,EH),H的社区影响值是H中所有节点权重的最小值,记作f(H),即:
(1)
定义2k-影响社区k-IC。给定无向图G=(V,E)和整数k,G的诱导子图H=(VH,EH)若是一个k-IC,需要满足以下属性:
(1) 连通性:H是连通的子图。
(2) 内聚性:H中的每个节点的度数至少为k,即H是一个k-core。
(3) 最大性:不存在G的诱导子图H′满足:①H′满足连通性和内聚性;②H′包含H;③f(H′)=f(H)。
(4) 非包含性:H不能包含社区影响值满足f(H′)>f(H)的H′。
例1考虑图3中带有权重的无向图G,G由{v1,v2,…,v16}共16个节点组成,括号内的数值为其权重,假设k=2、r=3。根据定义2,由节点集{v10,v11,v12,v13}形成的诱导子图是2-IC,其社区影响值为13。由节点集{v10,v11,v13}和{v11,v12,v13}形成的诱导子图均不是2-IC,因为它们的社区属性值也为13,且包含在由{v10,v11,v12,v13}形成的2-IC中,不满足最大性约束。由节点集{v9,v10,v11,v12,v13}形成的诱导子图也不是2-IC,因为其包含2-IC{v10,v11,v12,v13},不满足非包含性。

图3 网络图G
在许多实际应用中,人们通常对网络中影响值比其他社区的影响值大且重复性小的k-core感兴趣,因此本文的研究目标为:给定无向图G=(V,E),权重向量W和两个参数k和r,目标是找到具有最高影响值的前r个k-IC。
3 算法设计
本节首先介绍了W-D索引结构,然后提出了基于该索引的算法ITIC。
3.1 W-D索引结构
W-D索引是一种表状索引结构。每个节点对应其权重和度数以及一个存放其邻居节点的数组,节点的度数等于邻居节点的个数。W-D索引中按照权重由大到小对所有节点进行排序。
如表2所示,根据例1中的图G建立的W-D索引,以v5为例,v5的权重最大,排在索引的首位,度数为2,其邻居节点有{v3,v6}。

表2 W-D索引表示例
W-D索引在ITIC算法中可用于确定被取节点的顺序,以及是否对被取节点进行处理,同时可以加快节点之间邻居关系的判断,提高了k-IC的查询处理效率。
3.2 ITIC描述
ITIC主要处理过程如下:(1) 插入桶;(2) k-IC判定。
3.2.1插入处理
ITIC首先从W-D索引中取点,选取索引中未处理部分的首元素v,若节点v在索引中的度数满足大于等于k,将v插入相应的桶B[i]中进行处理,否则不处理,继续进行取点。
桶B[i]。要求每个桶B[i]中的节点满足条件:任意B[i]中的节点能够组成一个连通子图。
对B[i]中的节点保留如下存储结构:
桶度数(B-deg(v,Hm)),即vj在桶B[i]中的度数,其中:Hm是B[i]中的节点形成的诱导子图。
定义3DC点。在桶B[i]中与组成k-IC的节点直接相连的节点称为DC点。
节点标记flag的取值有如下4种:
(1)flag=0,表示节点未经判定的初始状态;
(2)flag=1,表示该节点是组成k-IC的节点;
(3)flag=2,表示该节点是DC点;
(4)flag=-1,表示经判定该节点一定不是组成k-IC的节点。
插入处理的具体过程如下:(1) 取到度数大于等于k的节点v后,遍历现有桶B[m],只要B[m]中存在节点u与v是邻居,就将此B[m]中的节点全部移加到临时桶b中,并删除当前B[m];(2) 遍历完成后,将v加到b中,更新b中节点的桶度数并移加全部节点到新桶B[n](v所在的桶记作B[n])。
例2依然以例1中的图G为例,当取到节点v11时,现有桶仅B[2]中有其邻居节点v10,因此v11插入后的桶如图4(a)所示。当取到节点v9时桶的分布如图4(b)所示,桶中的{v10,v11,v12,v13}是一个2-IC,因此v9是DC点。

(a) 取到v11时的桶(b) 取到v9时的桶
算法1给出了ITIC的伪代码描述。
算法1ITIC描述
输入:网络图G=(V,E),索引,参数k、r。
输出:top-rk-IC。
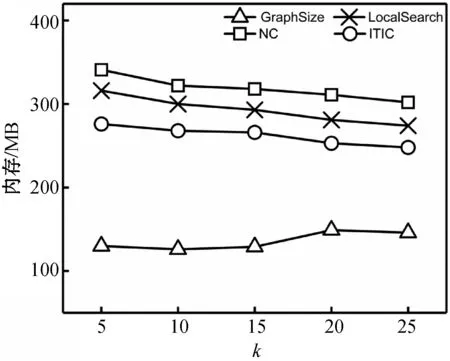
1.While(索引不为空&&|S| 2.取索引中未处理部分的首元素v; 3.If (v在度-邻索引中的度数 4.Else 5.flag(v)=0;b=∅; //标记flag,临时集合b 6.For (每个B[m]) 7.If(B[m]中存在节点u与v是邻居) 8.If (flag(u)==1&&flag(v)==0) 9.flag(v)=2; //DC点标记flag=2 10.把B[m]中的所有节点移加到b中; 11.删除B[m]; 12.v加入b中,更新b中节点的桶度数并 将所有节点移到新桶B[n]; 13.If (B[n]中节点满足定理3) 14.S←S∪JudK-IC(B[n],k); 3.2.2k-IC判定处理 当桶B[n]中插入节点v后,若达到判定条件,需要对B[n]进行k-IC判定。本节主要介绍k-IC判定策略。 定理1DC点一定不是组成k-IC的节点,包含DC点的k-core一定不是k-IC。 证明:根据DC点的定义,DC点直接与组成k-ICH的节点相连,并且易知DC点的影响值比H的社区属性值小。根据定义2,包含此DC点的k-core若满足最大性,需要包含H,因此不满足非包含性,此k-core一定不是k-IC。定理1得证。 证毕。 图3中G的诱导子图{v9,v10,v11,v12,v13}和{v1,v2,v3,v4}中分别包含DC点v9和v3,二者均不是2-IC。 定理2任意包含组成已得k-IC的节点(即flag=1的节点)的k-core一定不是新的k-IC。 证明:根据定义2的最大性,k-IC的子图一定不是新的k-IC;又根据定理1,无论k-IC还是k-IC的子图,加上DC点后组成的新的最大k-core都一定不是新的k-IC。定理2得证。 证毕。 根据定理2,包含k-IC中所有flag=1的节点的k-core和包含部分flag=1节点的k-core均不是新的k-IC,如图3中G的诱导子图{v9,v10,v11,v13}和{v1,v2,v3,v5,v6}均不是新的2-IC。 根据定理1和定理2,如果节点v是DC点,只需对v进行插入操作即可,然后返回取下一个节点。 引理1当B[n]中有多于k个flag=0的节点满足deg(u,Hn)≥k时,B[n]中可能存在k-IC。 定理3只有当v不是DC点同时满足deg(v,Hn)≥k,并且B[n]满足引理1时,可对B[n]进行k-IC判定。 证明:根据定理1和引理1易得证。 满足定理3时,对B[n]进行k-IC判定,算法2给出了k-IC判定算法的伪代码描述。 算法2JudK-IC(B[n],k) 输入:桶B[n],参数k。 输出:包含v的k-IC。 1.Tm=∅;R=∅; //临时集合Tm,返回结果集R 2.把B[n]中B-deg(u,Hn)≥k的节点u加入Tm; 3.求Tm中每个节点u的临时度数degTm(u,HTm); 4.If (Tm中全部节点均满足degTm(u,HTm)≥k) 5.R←只由flag=0的节点组成的最大连通分量; 6.Else 7.递归删除Tm中degTm(u,HTm) 8.If (Tm中degTm(u,HTm)≥k的节点个数>k) 9.R←只由flag=0的节点组成的最大连通分量; 10.Else return false; 11.If (R≠∅) 12.为R中的每个节点设置flag=1; 13.将Tm中flag=0的节点设置标记flag=-1; 14.returnR; k-IC判定的具体过程如下:(1) 把B[n]中桶度数B-deg(u,Hn)≥k的节点u加入临时集合Tm,并求Tm中每个节点u的临时度数degTm(u,HTm)。(2) 如果Tm中全部节点均满足degTm(u,HTm)≥k,则返回这些节点中只由flag=0的节点组成的最大连通分量;否则,递归删除Tm中degTm(u,HTm) 例3仍以例1中的图G为例,k=2、r=3。当节点v13插入桶B[4]时,B[4]满足定理3,如图5所示,对B[4]进行2-IC判定。将B[4]中满足桶度数B-deg( 图5 k-IC判定示例 u,Hn)≥2的节点v10、v11、v12、v13加入临时集合Tm,并求它们在Tm中的临时度数degTm(u,HTm),在此例中B-deg(u,Hn)=degTm(u,HTm),各节点均满足≥2,因此{v10,v11,v12,v13}是一个2-IC。 当取到节点v2时,从桶中共输出3个2-IC,分别为H1={v10,v11,v12,v13},H2={v14,v15,v16},H3={v1,v2,v4},社区属性值分别为f(H1)=13,f(H2)=9,f(H3)=8。至此已满足参数r=3,求得top-3 2-IC,算法结束。 在本节中,使用C++语言实现了文中提出的ITIC。环境配置为Intel Xeon W-2104 3.19 GHz CPU,32 GB内存,Windows 10操作系统。 本节将ITIC与之前效果较好的NC算法[4]和LocalSearch算法[10]进行性能分析比较。本文使用了两个真实网络数据集Wiki和Arabic验证算法性能。节点的权重为其PageRank值。表3总结了数据集的统计数据。在表3中,n和m分别表示网络中节点和边的数量,dmax和kmax分别表示网络的最大度数和最大核数。 表3 实验参数 图6描述了Wiki和Arabic两个数据集下,参数k对算法的影响。此处设置参数r=15不变,参数k的取值范围为{5,10,20,50}。可以看出,随着参数k的增大,NC算法的处理时间逐渐减少,ITIC和LocalSearch算法的处理时间逐渐增加,但两个数据集整体处理效率都表现为ITIC优于NC算法和LocalSearch算法。NC算法是从权重小的节点开始处理,需要处理完所有节点之后才能得到结果;LocalSearch算法需要先估算局部搜索图的大小,遍历局部图中的所有节点找到全部keys,然后才能得到结果;而ITIC是从权重大的节点开始处理,处理权重较大的部分节点就能得到结果,不需要提前估算局部图的大小,并且不需要频繁计算图中的连通分量,使得ITIC效率更高。 图6 参数k对算法的影响(r=15) 图7描述了Wiki和Arabic两个数据集下,参数r对算法的影响。此处设置参数k=15不变,参数r的取值范围为{5,10,20,50,100}。可以看出,两个数据集都表现为整体处理时间ITIC优于NC算法和LocalSearch算法。其中当参数r不是特别大时,ITIC优势明显,因为ITIC为渐进输出,只需要处理部分权重较大的节点就能求得top-r的结果,使得ITIC效率更高。 图7 参数r对算法的影响(k=15) 图8所示为当r=15时算法在不同k下的内存占用大小比较,其中k的取值范围为{5,10,15,20,25}。可以看出,对于Wiki和Arabic两个网络,ITIC消耗的内存比NC算法和LocalSearch算法都少,因为ITIC根据参数k进行了过滤,k越大,过滤掉的节点越多,并且ITIC不需要频繁计算图中的连通分量,使得ITIC消耗的内存更小。 (a) Wiki 通过上述多种不同的实验测试,验证了本文提出的ITIC的有效性,无论是变化参数k还是参数r,ITIC在处理时间和内存占用方面都优于现有算法,可以满足人们的日常需求。 本文研究了网络中k-IC的top-r查询问题。首先,提出了用W-D索引来管理网络,该索引结构可以确定被取节点的顺序,且对不满足条件的节点进行过滤,同时可以加快对节点之间邻居关系的判断,提高了k-IC的查询处理效率。然后,提出了k-IC的top-r查询优化算法:ITIC。该算法从权重较大的节点开始处理,一般情况下,只需处理部分节点即可求得结果,并且不需要频繁地计算图中的连通分量;另外,ITIC渐进输出k-IC,当k-IC的数量满足用户的需求时,用户可以在任意时间终止算法。最后,通过实验验证了ITIC的有效性。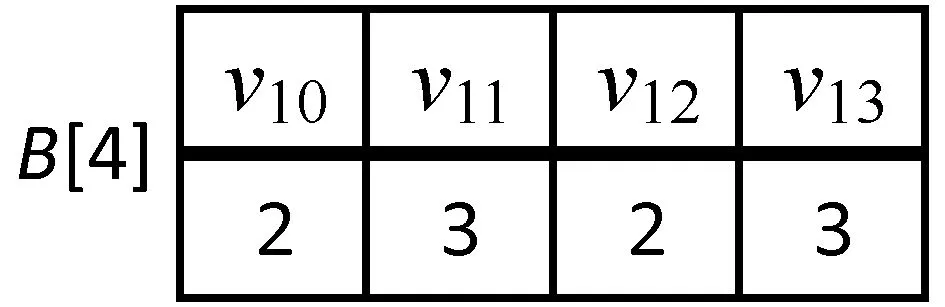
4 实验与结果分析



5 结 语

