基于半参数广义可加模型的社会消费品零售总额影响因素研究

凌兰兰

(安徽建筑大学 数理学院, 合肥 230601)

现阶段我国经济正处于高速增长阶段转向高质量发展阶段,主要矛盾也已发生重大改变。为解决人民日益增长的美好生活的需要和不平衡不充分发展之间的矛盾,必须坚定实施扩大内需战略。

作为反映全社会消费情况的主要指标,社会消费品零售总额涉及范围较广,不仅包括售给个人用于生活消费用的商品和建筑材料,也包括售给社会集团用作非生产、非经营的商品和餐饮服务所取得的收入金额等。它不仅直接反映了国内消费需求,还可以衡量社会经济景气程度。扩大国内投资、刺激国内消费和扩大外贸出口常被称为经济增长的“三驾马车”,只有保证经济发展才能扩大消费,积极促进国家或地区经济增长。随着国内城镇化扩大和人均可支配收入增加,消费在经济增长中的重要性日渐凸显。世界各国尤其是发达国家,为了发展经济,不断强调扩大国内消费、促进消费升级、培育消费热点。因此,研究社会消费品零售总额的影响因素对处在发展关键期的我国具有重要的经济意义。

1 文献综述

关于影响因素的选取,杨远裴[1]从消费需求、商品供给等4个层面初步选取了10个变量,用随机森林回归模型从中选择出了6个主要影响变量,包括广义货币供应量(M2)、狭义货币供应量(M1)、国内生产总值(GDP)固定资产投资额、邮电业务量和商品房销售额,使用这6个变量构建了含有自变量的动态回归模型进行预测;李小星和徐永利[2]采用函数型数据分析方法对数据进行了预测,将数据分为长期趋势成分和季节性成分分别加以预测;梁红梅和赵宏宝[3]研究发现人均可支配收入可以正向推动社会消费品零售总额的增长;马强等[4]基于乘积季节模型对数据进行时间序列分析,确定最终模型为ARIMA(1,1,1)(1,1,0);蒋翠清和乔晗[5]在构建安徽省社会消费品零售总额累计增幅预测模型时,融合了股市数据;韩玉锦[6]建立了灰色预测模型GM(1,1)预测新冠病毒对武汉地区社会消费品零售总额的影响值大小。目前关于该问题的研究多采用多元线性回归和时间序列方法,但多元线性回归法往往忽略自变量之间非线性的因果关系。为克服这个缺陷,本文首次将半参数回归模型运用到对社会消费品零售总额的影响因素的研究。

由于半参数回归模型具有高度的灵活性和适应性,国内外将其应用到各个领域的研究越来越多。关于半参数回归方法的详细介绍及求解过程,梅长林和王宁[7]、Ferraty和Vieu[8]均在其著作中有详细说明;黄宏超等[9]分别用半参数回归模型和传统参数模型来描述华北落叶松和白桦树高与胸径的关系,比较发现半参数回归模型的拟合效果明显更佳;马馨悦[10]为研究余额宝的影响因素,分析变量的线性或非线性影响及交互作用,从而建立了半参数可加模型;李呈呈等[11]将半参数分位数回归模型应用于老年人医疗费用的研究;鲁万波和陈映彤[12]基于半参数误差修正模型对中国市场汇率进行预测研究。然而在已有半参数回归研究中,不少学者忽略了变量间的交互作用。

选取2016年7月至2022年6月的月度数据,经过灰色关联分析和单变量非线性效应分析,筛选确定5个影响因素,将其中的2个非线性影响因素作为半参数广义可加模型的非线性部分,并考虑了它们之间是否存在交互效应,发现考虑交互作用而建立的模型比不考虑交互作用的模型解释性更好,从而建立了含有交互项的半参数广义可加模型。

2 变量选取与指标设计

通过对相关文献的总结、比较,不难发现社会消费品零售总额受一些经济指标的影响,故初步筛选出7个经济自变量如表1所示。

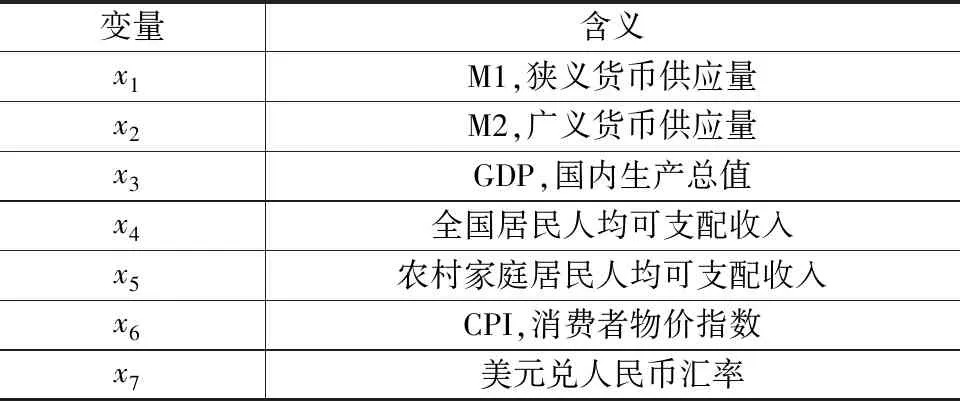
表1 变量选取与含义

选取的数据为2016年7月至2022年6月的月度数据,来自国家统计局和中国人民银行。鉴于GDP、全国居民人均可支配收入和农村家庭居民人均可支配收入均是季度数据,故借用Eviews软件的插值法将其转化为月度数据。考虑到国家统计局不单独开展1月和2月的零售总额数据,故剔除每年1～2月的数据,对剩下60个月的数据进行建模研究。

3 理论模型

3.1 灰色关联分析

灰色关联分析方法被用于描述因素之间变化趋势的相似或相异程度,又称为“灰色关联度”,若变化趋势较为一致,则二者关联程度较大;反之,则较小。该方法的具体计算步骤如下。

第一步:确定母序列和子序列。

母序列:

(1)

子序列:

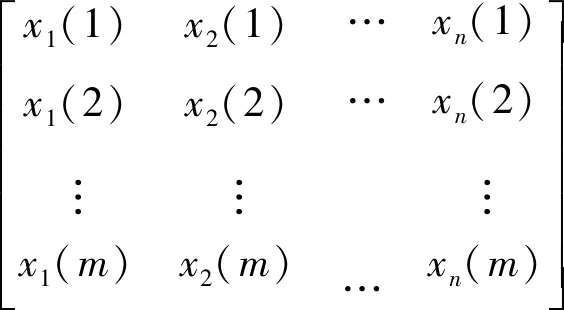
(2)

第二步:对母序列和子序列进行初值化处理。

(3)

(4)

第三步:计算子序列中各个指标与母序列相对应指标的关联系数。

(5)

式中:i,j=1,2,…,n,;k=1,2,…,m;ηj(k)为X0(k)和Xj(k)间的关联系数;ρ∈[0,1],一般取0.5。

第四步:计算第j个对象的灰色关联度。

(6)

3.2 半参数广义可加模型

在许多实际问题中,某个变量Y往往与变量X1,X2,…,Xp有关,但这种相关关系经常不甚明确,因此只能说Y部分由X1,X2,…,Xp的取值决定。这时我们可以认为Y的取值由两部分构成:一部分由X1,X2,…,Xp通过某个函数关系m(X1,X2,…,Xp)确定;另一部分为随机因素,记为ε,于是Y与X1,X2,…,Xp的关系可表示为

Y=m(X1,X2,…,Xp)+ε

(7)

式中:Y为因变量;X1,X2,…,Xp称为自变量;m(X1,X2,…,Xp)称为回归函数;Y与X1,X2,…,Xp的关系称为回归关系;ε称为误差项,并假定E(ε)=0。如果函数形式是已知的,即

m(X1,X2,…,Xp)=

f(X1,X2,…,Xp;β1,β2,…,βr)

(8)

式中:f是已知函数;β1,β2,…,βr是未知参数。

式(7)为参数回归模型。然而,如果不假定回归函数m(X1,X2,…,Xp)的具体形式,只要求p元回归函数是连续或光滑的,此时式(7)为非参数回归模型。这类模型具有高度的灵活性,但是当自变量的维数增加时,常常会出现难以控制的维数灾难问题,为了克服该缺陷,半参数广义可加模型应运而生。

(9)

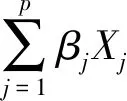
4 实证分析

根据上面对灰色关联度计算步骤的描述,借助Matlab软件编程求解,得到各相关因子与社会消费品零售总额的灰色关联度(表2)。

表2 灰色关联度

由表2可知,影响社会消费品零售总额的相关因子程度为:x1>x4>x3>x2>x5>x6>x7,且前5个相关因子的影响程度显著大于后2个。

4.1 单变量分析

当因变量不通过正态性检验时,即不能建立线性回归模型,此时建立半参数回归模型才具有意义,通过QQ图(图1)来检验社会消费品零售总额的正态性。

鉴别样本数据是否近似于正态分布,只需看QQ图上的点是否近似地在45°的直线上。若散点图是直线则说明是正态分布,且直线的斜率和截距分别表示标准差和均值。显然图1中大部分数据偏离该直线,所以社会消费品零售总额不服从正态分布,可以采用半参数回归模型对其进行建模。

接下来计算各自变量与社会消费品零售总额的线性相关系数,由R软件的cor(·)函数实现(图2)。

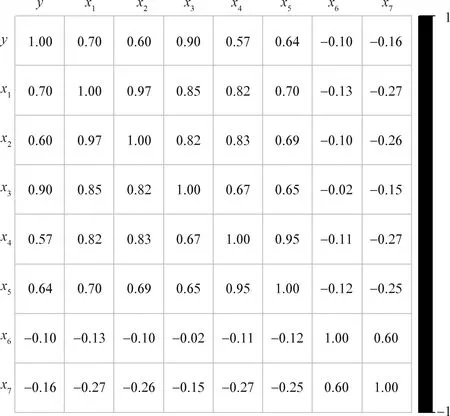
图2 各变量间的相关系数

显然x6、x7与y的相关系数极小,因此CPI、美元兑人民币汇率与社会消费品零售总额间不存在线性关系,于是考虑它们之间是否存在非线性关系。

由表3和表4的最后一列P可知,在显著性水平为0.05情况下,x6和x7的非线性效应不显著,因此x6、x7与y也不存在非线性关系,这与表1灰色关联度计算结果相一致。x6、x7与y的关联度最小,于是将这2个变量剔除,对剩下5个自变量进行研究。

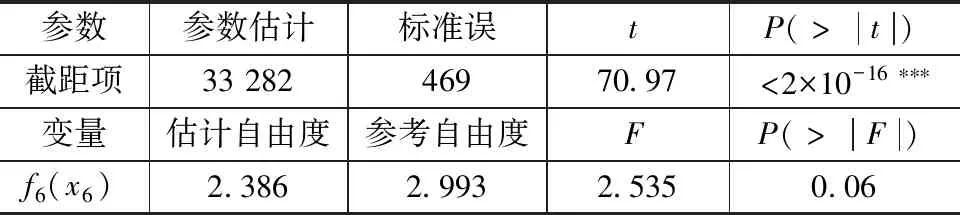
表3 x6单变量分析结果

由图2可知,x3与y的相关系数达到0.9,两者之间存在高度正相关,因此将x3作为半参数广义可加模型的线性部分。接下来考虑其他4个自变量与因变量之间的关系。

图3和图4分别是考虑x1、x4作为单变量时对因变量的非线性影响。实线越弯曲表明非线性作用越显著。显然,x1非线性效果不显著,x5同样不显著,x2与x4的非线性效果较显著,恰好印证了它们与y的线性相关系数最小。因此,选取x2与x4作为模型的非参数部分,x1、x3与x5作为线性部分,得到部分回归结果如表5所示。

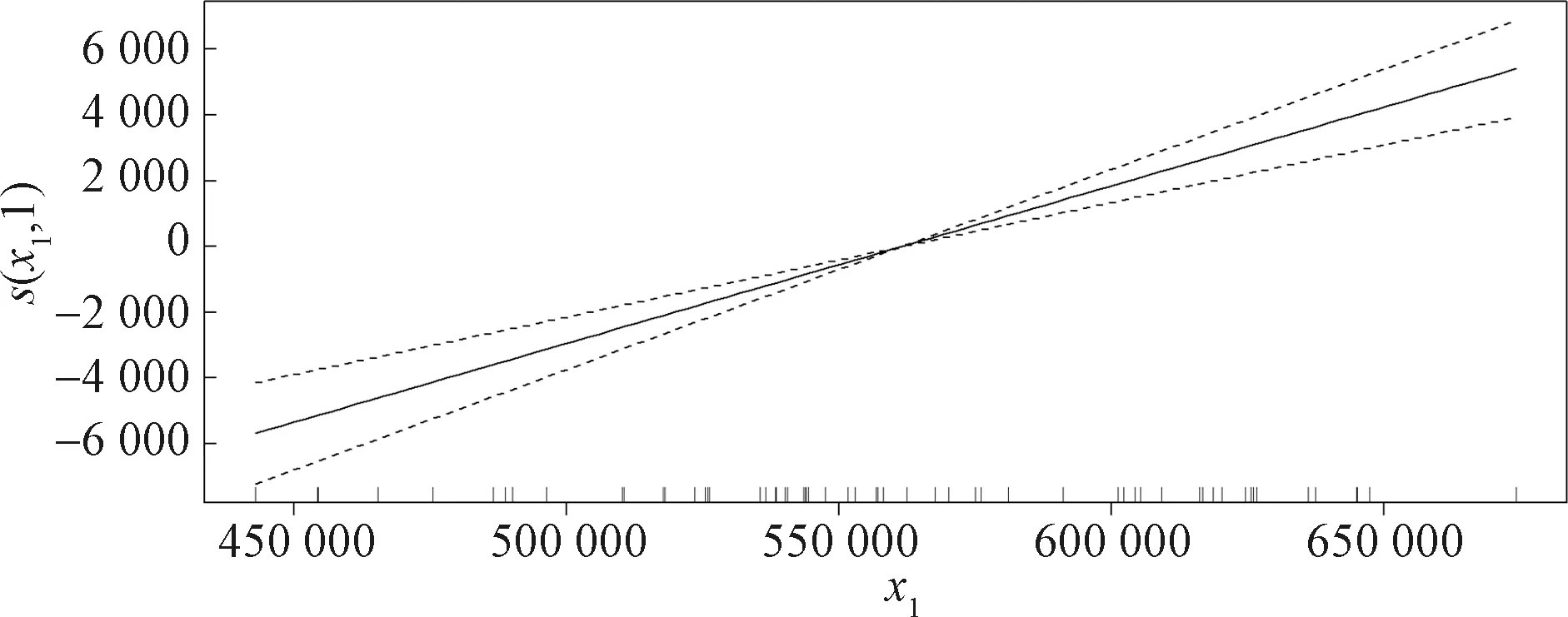
图3 x1单变量分析效应

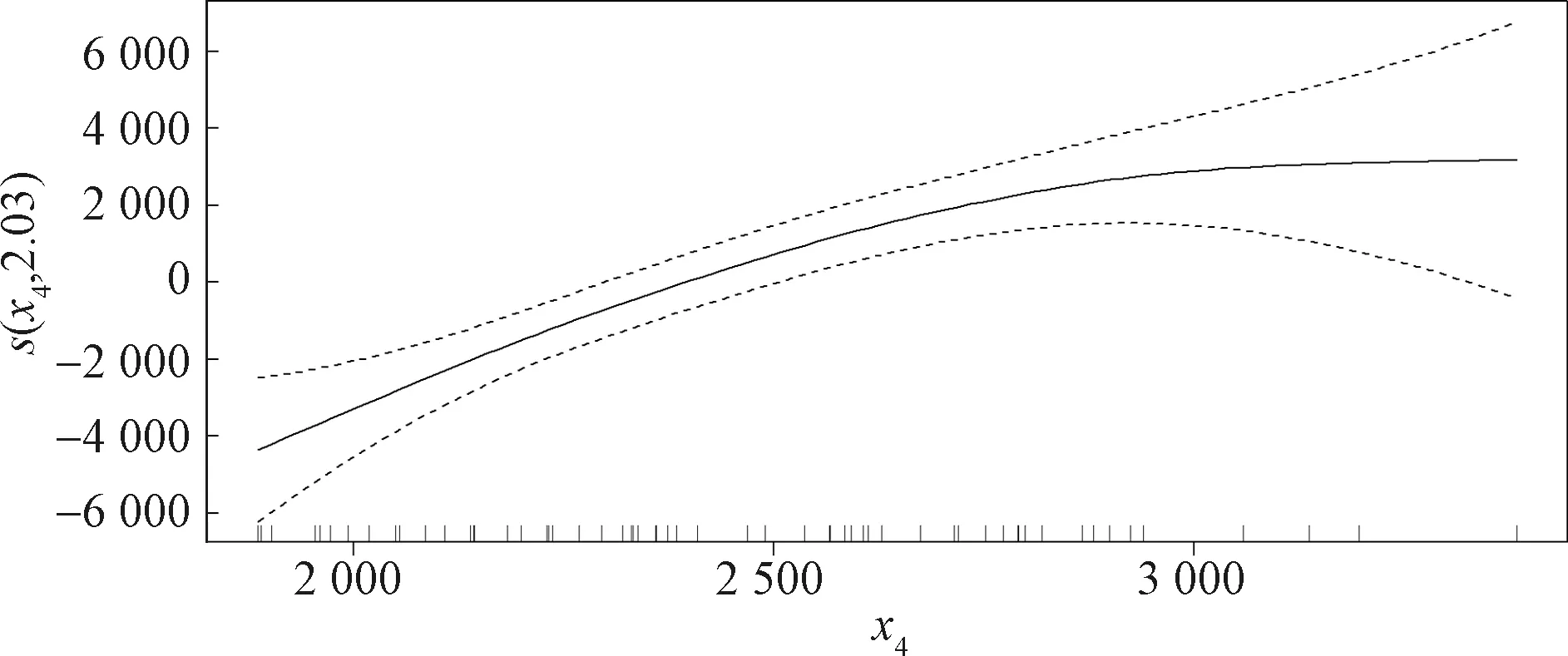
图4 x4单变量分析效应

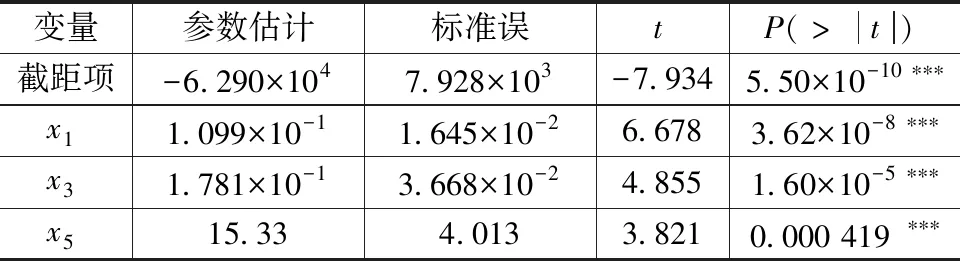
表5 模型的线性部分回归结果

其中输出R2结果为0.96,表明模型的解释能力为96%,可解释偏差输出结果为97.1%,表明模型的可解释偏差为97.1%,两项结果可以看出模型的解释能力很好。由表5和表6可知,M1,GDP和农村家庭居民人均可支配收入对社会消费品零售总额均具有正线性影响,且所有变量均通过显著性检验,所以可初步得到模型为

表6 模型非线性部分回归结果

y=-62 900+0.109 9x1+0.178 1x3+

15.33x5+f1(x2)+f2(x4)+ε

(9)

4.2 交互作用分析

值得注意的是,非参数广义可加模型的非线性变量间有时会存在交互效应现象,对两个自变量而言,这种现象表现为一个自变量对因变量的效应会随着另一个自变量的变化而变化。于是对x2和x4进行交互作用分析,得到交互作用效应如图5所示。

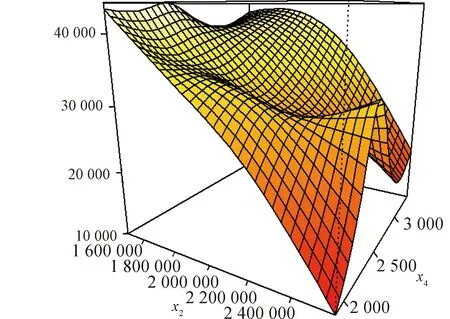
图5 x2和x4的交互作用效应

表7显示在考虑交互作用时,所有自变量包括x2和x4的交互项均通过显著性检验,且模型输出R2结果为0.977,表明模型的解释能力为97.7%,可解释偏差输出结果为98.4%,表明模型的可解释偏差为98.4%,相较于模型(9)效果更好。图5纵轴表示因变量预测值,可以看出M2和全国人均可支配收入交互效用明显。人均可支配收入较低时,M2越大会使得社会消费品零售总额越低;在M2接近260 000元/人、人均可支配收入略小于2 000元时,社会消费品零售总额最低;M2较大时,人均可支配收入越接近于2 500元/人,社会消费品零售总额越高;M2和人均可支配收入同时较低时,会使得社会消费品零售总额达到极大值。

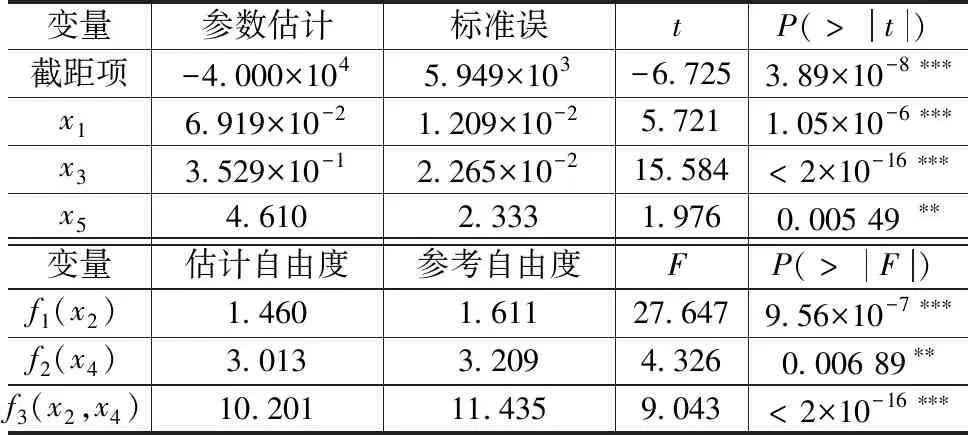
表7 交互作用分析结果

综上,关于全国社会消费品零售总额的影响因素分析,最终建立模型。

y=-40 000+0.069 19x1+0.352 9x3+

4.61x5+f1(x2)+f2(x4)+f3(x1,x4)+ε

(10)

5 结论

基于半参数广义可加模型的思想,本文对全国社会消费品零售总额的影响因素进行了研究。首先对初步选取的7个可能影响因素进行了灰色关联分析和相关系数计算,并对每个影响因素都单独进行了非线性效应分析。结果表明,CPI和美元兑人民币汇率2个影响因子与社会消费品零售总额之间不存在线性或非线性关系,而这也恰好印证了这2个影响因子与社会消费品零售总额之间的灰色关联度最低。

上述分析发现M1、GDP和农村家庭居民人均可支配收入3个自变量对因变量均具有正线性影响,M2和全国人均可支配收入2个自变量对因变量具有非线性影响,其中GDP和社会消费品零售总额高度正相关,因此可以初步建立模型(9)。

进一步考虑到两个非线性项之间可能存在交互效应,于是对它们进行交互效应分析。结果显示,M2和全国人均可支配收入交互效用显著:人均可支配收入较低时,M2越大会使得社会消费品零售总额越低;M2较大时,人均可支配收入越接近于2 500元/人,社会消费品零售总额越高。因此,加入M2和全国人均可支配收入的交互项重新建模得到模型(10)。通过比较,得到模型(10)的判定系数R2和可解释偏差结果都明显优于模型(9),说明模型(10)的解释能力更强,因此最终选定模型(10)。