基于特征工程的建设工程造价指数预测模型构建

刘 耘, 陆 军

(新疆大学 建筑工程学院, 乌鲁木齐 830046)

工程造价指数是常见的投资估算指标,是一种反映特定时期下,人工费、材料费、机械材料租赁费用等要素对工程造价影响的一种指数。造价指数具有时限性,且只能反映特定时间内工程造价的变动趋势,由于建设周期较长,在建设项目投机估算阶段需要将未来几年工期内造价指数作为参考指标,因此需要对工程指数进行预测。造价指数预测主要方法包括定性专家预测法、主观概率法、交叉影响法、定量时间序列预测法、回归预测法、灰色预测法[1]。基于机器学习的回归预测作为一种回归预测方法,已经被广泛地应用到生产生活之中。相比于传统预测方法,机器学习预测学习能力强,预测误差小,能够更好地处理复杂的数据预测问题。

1 相关研究

基于机器学习的造价指数预测模型构建,国内学者主要研究方向在选定算法后的参数优化,来提升模型的预测精度。选择较多的有神经网络和集成模型。

神经网络是根据模拟人脑神经信息传递、处理等机制的算法,基础神经网络模型有BP(back propagation)神经网络模型、卷积神经网络网络模型等,其中BP神经网络模型是通过误差反向传播加快收敛速度的模型。罗泽民和布优月[2]选用GM(1,1)和BP神经网络,通过参数优化对神经网络组合模型进行了研究。刘伟军和李念[3]结合了GM(1,1)模型、思维进化算法和神经网络算法,利用思维进化算法提升模型的预测精度。朱曦等[4]在公路运价指数预测中选用极限学习机神经网络快速高效地完成了模型构建并提升预测能力。刘传和陈彦晖[5]在股指波动率的长短期记忆(long short-term memory,LSTM)神经网络模型构建前用经验模态分解和样本熵对数据进行了预处理,从而提高了模型的预测效果。

集成学习是指将多个弱学习模型或多个模型进行结合构成一个具有更强学习能力的模型,基于弱学习器的有随机森林算法、极端梯度提升(extreme gradient boosting,XGBoost)和神经网络梯度提升(neural network gradient boosting,NGBoost)等。张旺等[6]在变电站基础设施项目投资算预测模型中选用XGBoost构建预测模型,结果表明XGBoost的预测精度高于线性回归模型和神经网络。罗凤娥等[7]在基于数据挖掘技术的航班预测综述中提出随机森林算法的优点在于高维数据处理上的优异性,但由于数据噪音易导致模型过拟合。黄颖和杨会杰[8]在金融时间预测模型中选用XGBoost对数据中的特征进行提取。多模型集成中Meseret等[9]集成了线性回归、支持向量机(support vector machine,SVM)和梯度增强算法来进行公路项目的成本预测。Sharma等[10]在数据优化的基础上,利用机器学习的工具,构建一个关于工程造价的环境、资源和时间构成的函数,结果表明梯度增强树在与随机森林、神经网络、高斯回归对比中,在各个方面都具有最佳的性能。

指数预测的模型构建以模型为主,通过模型优化对模型效果进行提升,并根据不同的数据特征进行模型合理选择,数据处理是模型构建和优化的重要思路,数据特征的处理反映了研究人员数据的理解程度和数据的重要特征,基于特征工程构建模型能深度挖掘数据中信息的同时也能对后续的相关研究数据的处理提供重要的参考价值。

为构建一个能够应用于实际工程的造价指数预测模型,本文重点研究基于特征工程和参数优化的模型构建,在优化基础算法基础上,通过特征筛选和特征填充,为造价指数预测模型选择合适的特征工程处理方式和模型优化参数,从而构建一个预测能力较好的预测模型。

2 数据与指标选取和预处理

2.1 数据来源

本文研究对象是U市造价指数预测,数据来源主要是U市工程信息信息网发布的U市2012年1月至2021年10月建设工程综合价格信息和建设工程造价信息网发布的2021—2012年省会城市住宅建安工程造价指标,单位为元/m2。

主要数据特征包括时间、材料费、人工费和机器租赁费10年间变化趋势。

2.2 数据特征工程

模型构建前的数据挖掘包括数据收集与过滤、数据预处理、数据变换等[12]。其中的数据特征工程是专门对数据挖掘中特征处理方法,特征工程的特征处理包括特征清洗、特征预处理和特征衍生,其中特征预处理包括单特征的数据归一化、离散连续化和缺失值处理、多特征的降维和特征筛选等。

2.2.1 数据基本描述

数据样本量为118个,578个数据特征,数据结构为小样本、高纬度数据集。

2.2.2 数据填充

针对数据缺失问题,处理方法是对数据进行填充或对大量缺失特征信息进行删除,为保证信息完整性,进行缺失数据填充。通过单变量插补和多变量插补,生成了最初两组数据,分别是均值填充数据集和随机森林填充数据集。

2.2.3 特征选择

由于高纬度数据特征易导致模型学习成本增加,导致模型拟合能力差,通过特征工程需要对数据特征进行筛选,减少特征数量。

采用过滤法的F检验是指通过计算特征相关性和阈值,选取阈值之内的特征,采用嵌入法中的树模型将特征选择嵌入模型的构建,通过模型选择重要性较高的特征,采用包裹法的递归特征消除法(recursive feature elimination, RFE),通过每次选择不同的特征子集组合并评价,最终选择最优的特征子集。

2.2.4 特征降维

选用主成分分析法(principal components analysis,PCA)通过数学变换将原本高纬度的数据映射在低纬度空间之上,从而便于计算和提高部分模型的整体性能。

2.2.5 特征子集构建

通过特征工程数据填充,特征选择和特征降维数据特征子集如表1所示。由表1特征数量可知,不同特征处理方式下,数据特征数量不同,为模型构建提供不同特征子集。

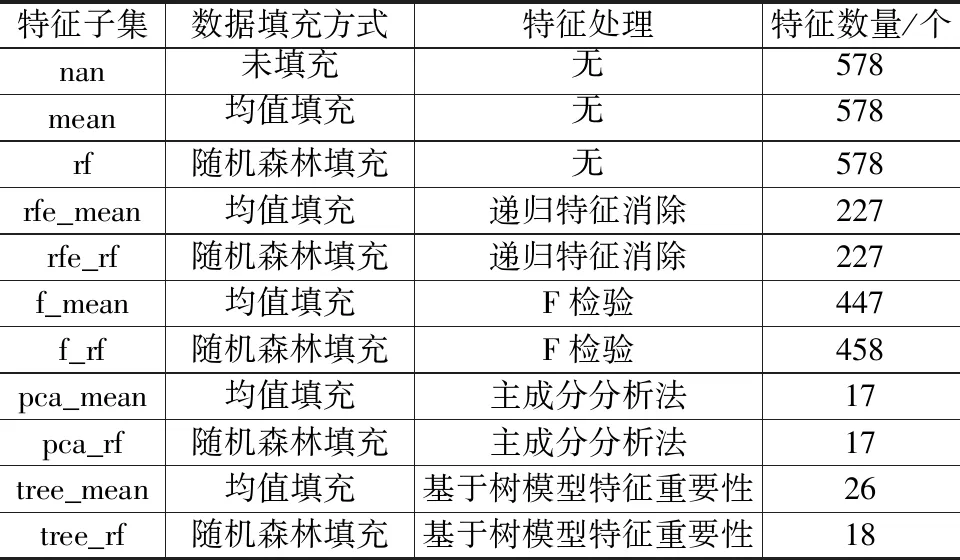
表1 特征工程处理后的特征子集

2.3 模型构建和模型评估

2.3.1 模型评价指标

将造价数据分为训练集和测试集。取2012—2020年的数据作为模型的训练集,同时对模型进行交叉验证(cross validation,CV),作为模型稳定性的评价指标,5折交叉验证是指将数据分成5份,依次使用其中的一份数据作为测试集数据,其余4份为训练集,平均测试集上预测结果作为模型的交叉验证值。测试集为2021年10个月的数据,作为模型泛化能力参考。

预测模型误差一般选用均方根误差(root mean square error,RMSE)表示,用以衡量机器学习中观测值和真实值之间误差的标准,表达式为

(1)

平均绝对百分比误差(mean absolute percentage error,MAPE)是一种描述预测精准度的指标,表达式为

(2)

式中:f(xi)为第i个样本的预测值;yi为第i个样本的真实值;m为样本量。

2.3.2 XGBoost模型构建

XGBoost是一种极端梯度提升树模型。不同于一般梯度提升树模型,XGBoost参数量多,性能提升空间大,需要对模型参数空间进行参数搜索,寻找参数之间的较优组合,对模型性能进行优化,采用贝叶斯优化搜索的参数有最大深度(max_depth)、树模型生成数量(num_boost_round)、学习率(eta)、重采样(subsample)、节点样本二阶导和的最小值(min_child_weight)、L1正则化系数(alpha)、L2正则化系数(lambda),模型默认参数为XGBoost库下默认设置,设置num_boost_round为100,搜索空间为XGBoost库文档给出的参考空间。经过参数优化后(表2),各个特征子集最优参数模型和模型预测误差如表3所示。默认参数构建的训练集、测试集和交叉验证集误差分别记为default_xgb_train、default_xgb_test、default_xgb_cv;参数优化后的训练集、测试集和交叉验证集误差分别记为opt_xgb_train、opt_xgb_test、opt_xgb_cv。

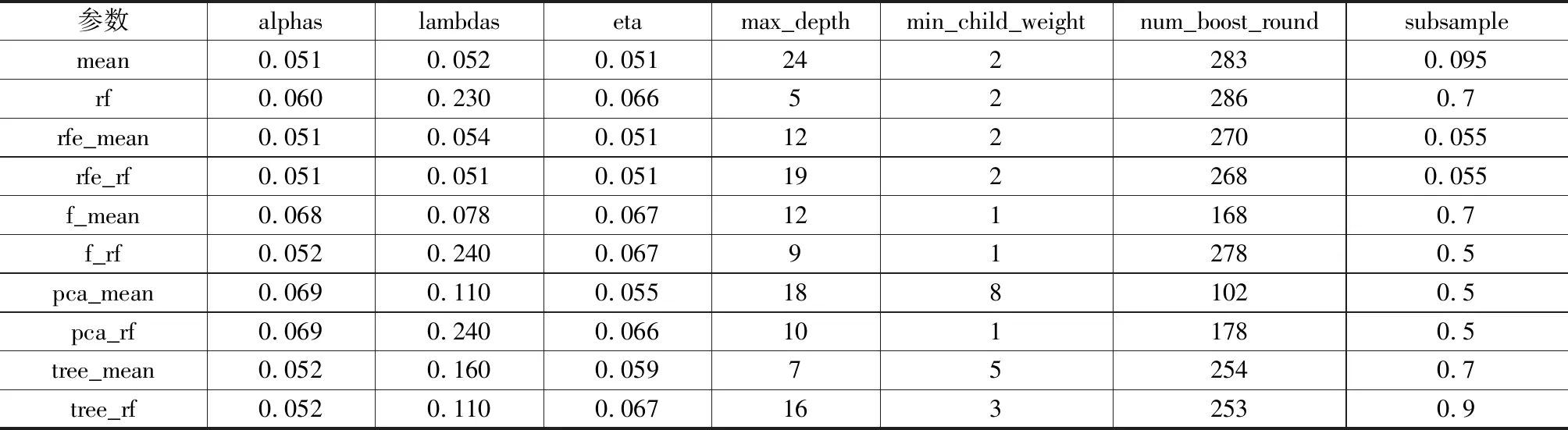
表2 XGBoost各特征子集优化后参数

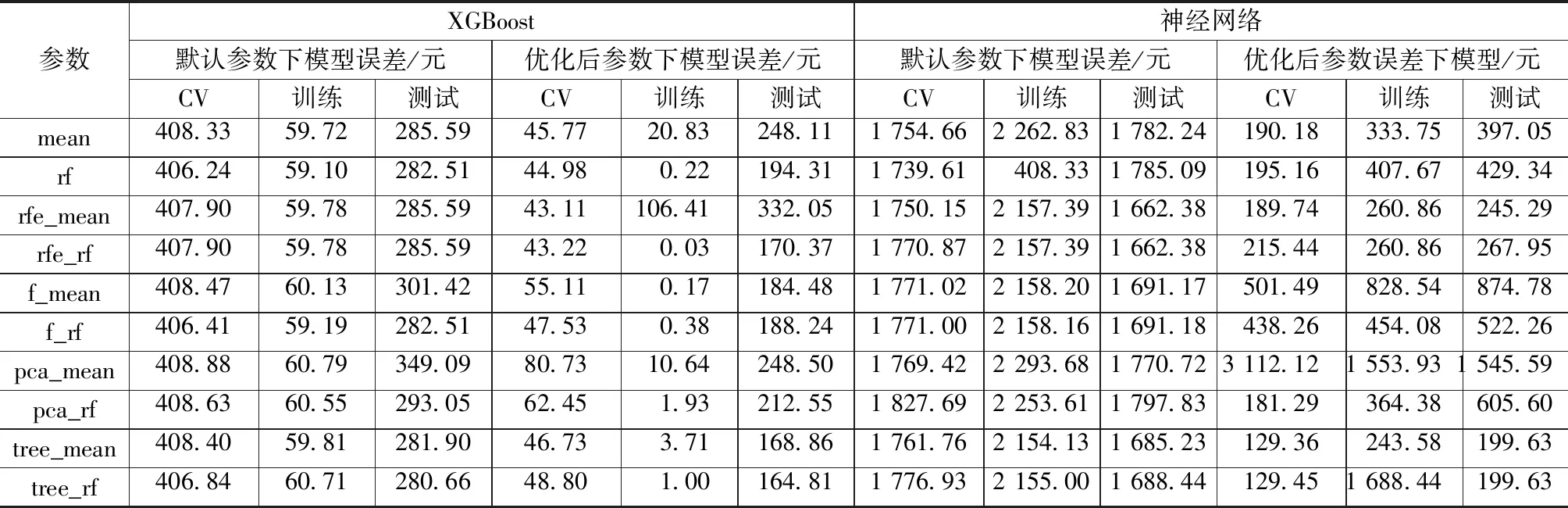
表3 XGBoost和神经网络误差对照

2.3.3 神经网络模型搭建

通过PyTorch构建一个4层神经网络,层级结构为全连接反向传播神经网络,分为输入层、隐藏层和输出层。输入层输入数据特征,隐藏层为4层,每层神经元数量通过超参数优化得出,输出层为1个神经元。默认神经网络模型的神经元个数为100个/层,不设置梯度提升算法和学习率,迭代次数为500次。

采用贝叶斯优化对每个特征子集构建的模型进行参数搜索,参数空间为[1,100],梯度提升算法的搜索空间为Adam算法、AdaDelta算法和AdaGrad算法,学习率搜索空间为[0.000 01,0.1]。

模型参数搜索完成后,参数如表4所示,对模型的预测误差进行对比,如图1所示默认参数构建的训练集、测试集和交叉验证集误差分别是default_ANN_train、default_ANN_test、default_ANN_cv;参数优化后的训练集、测试集和交叉验证集误差分别是opt_ANN_train、opt_ANN_test、opt_ANN_cv,神经网络默认参数和优化后的模型误差如图2神经网络误差所示。

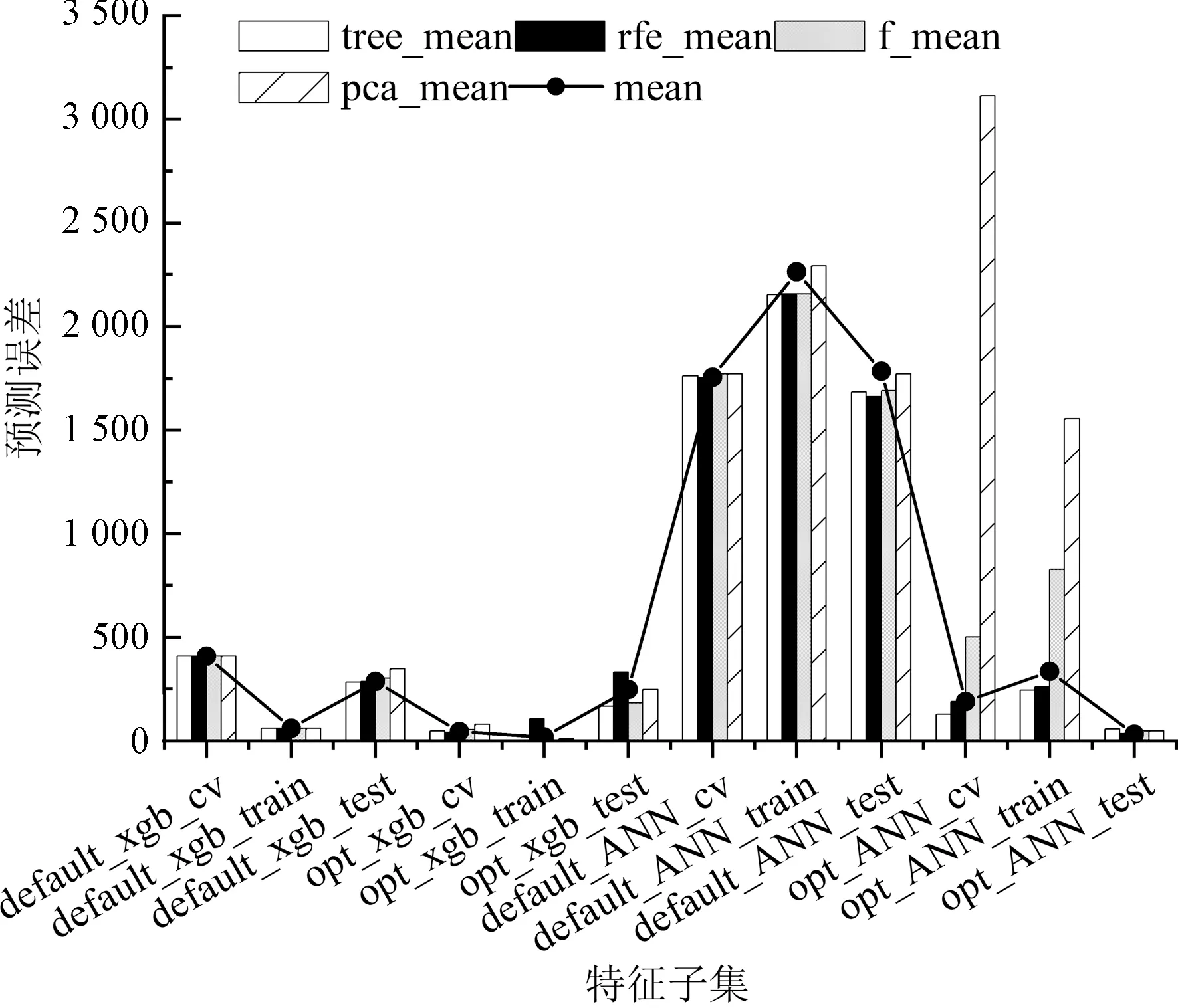
图1 随机森林填充后的各个模型误差

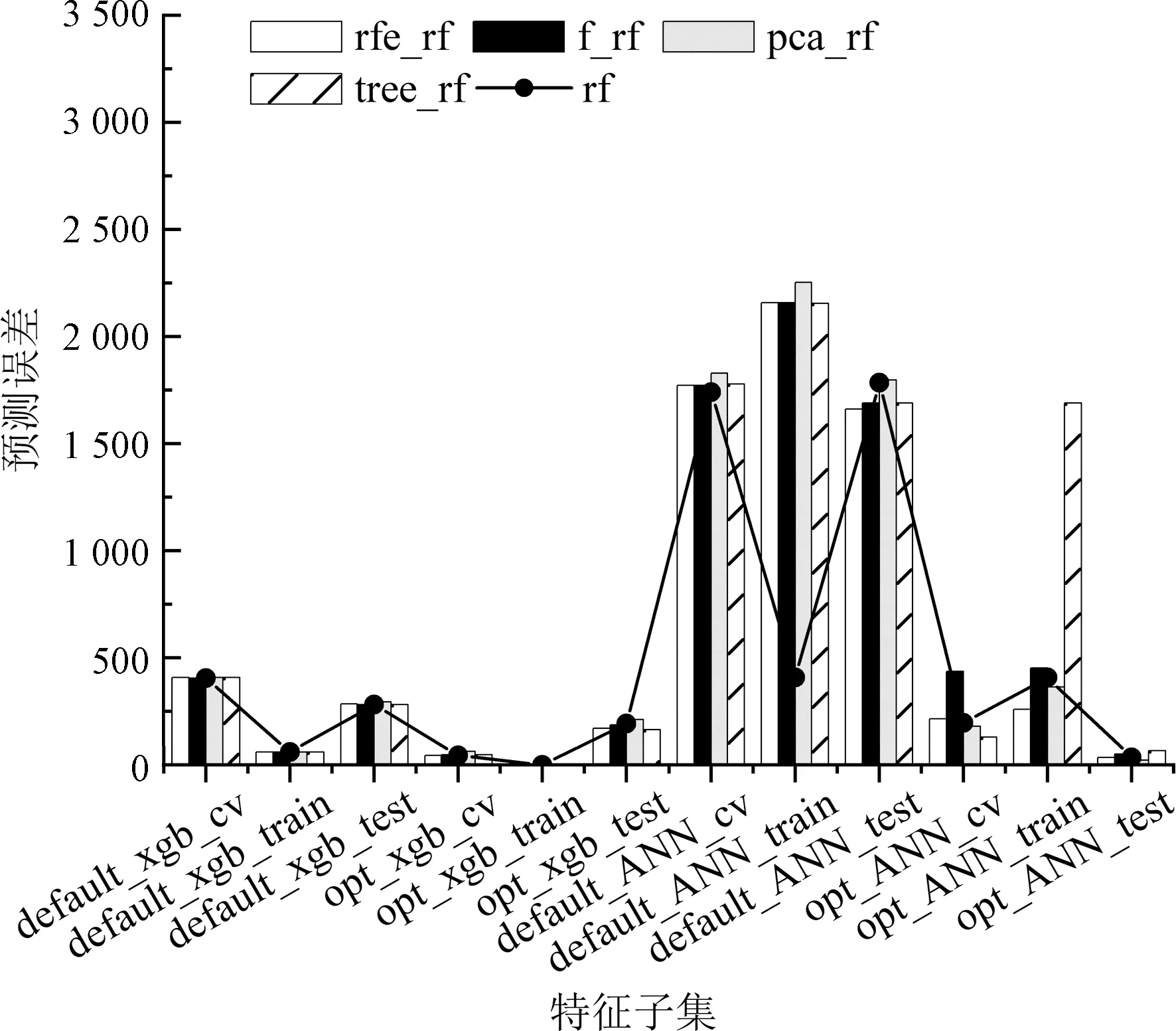
图2 均值填充后的各个模型误差

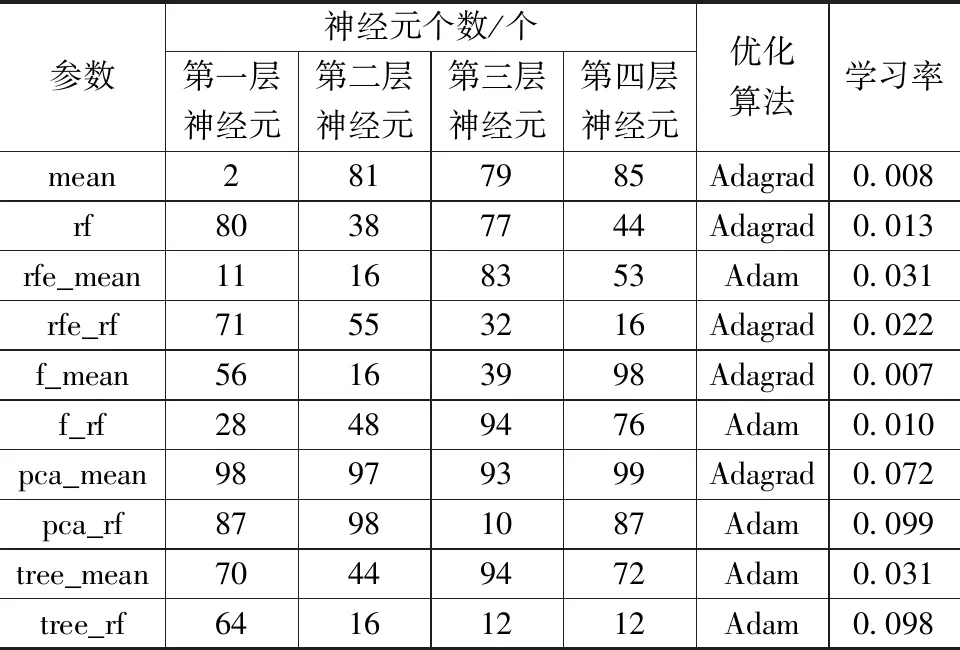
表4 神经网络各特征子集优化后参数

2.3.4 模型选择和评估

首先,根据数据缺失值处理和特征选择,完成模型构建前的数据准备工作;其次是模型参数优化;最后,对模型拟合能力、泛化能力和稳定性进行评价,遴选合适的特征工程方式并构建模型。

神经网络默认参数下,随机森林填充训练误差小于均值填充误差。

2)特征筛选。如图1和图2所示,特征筛选后的大部分模型预测误差有降低但整体降低不明显,在特定模型上的提升效果明显,如均值填充后,优化后的XGBoost模型在训练集上得到了较大的提升。但也有模型在特征筛选后预测误差增加,如默认参数下神经网络训练误差。因此,特征筛选需要根据具体模型效果进行使用。

3)参数优化。由表3、图3和图4可知,参数优化后的XGBoost模型训练误差和交叉验证误差显著下降,测试集误差大部分有所下降。如表3、图5和图6所示,相比于默认参数模型,除了数据降维后的模型,参数优化后的神经网络模型在训练误差、测试误差和交叉验证误差都有了显著地降低。

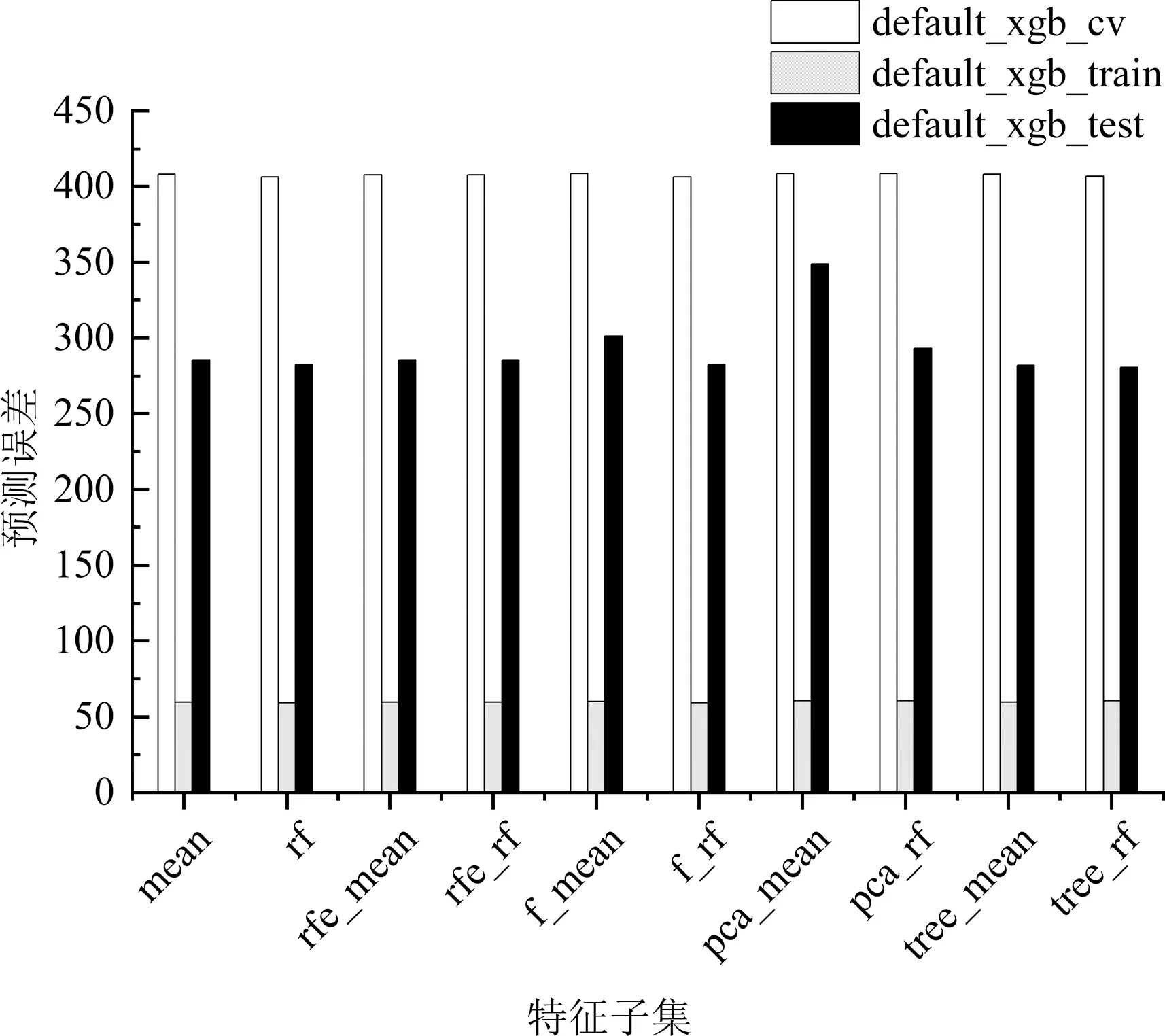
图3 默认参数下各个XGBoost的误差

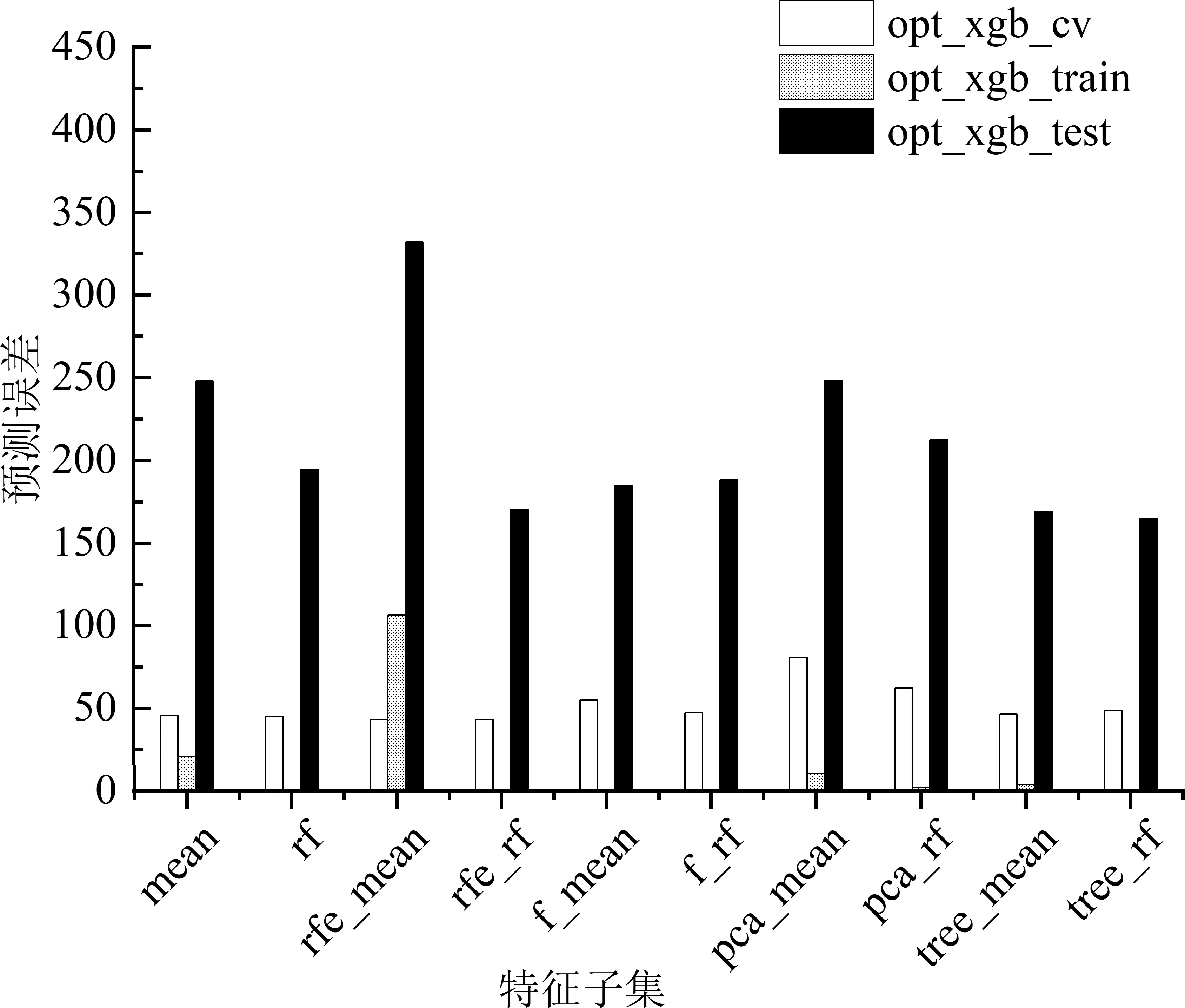
图4 优化参数后各个XGBoost模型的误差

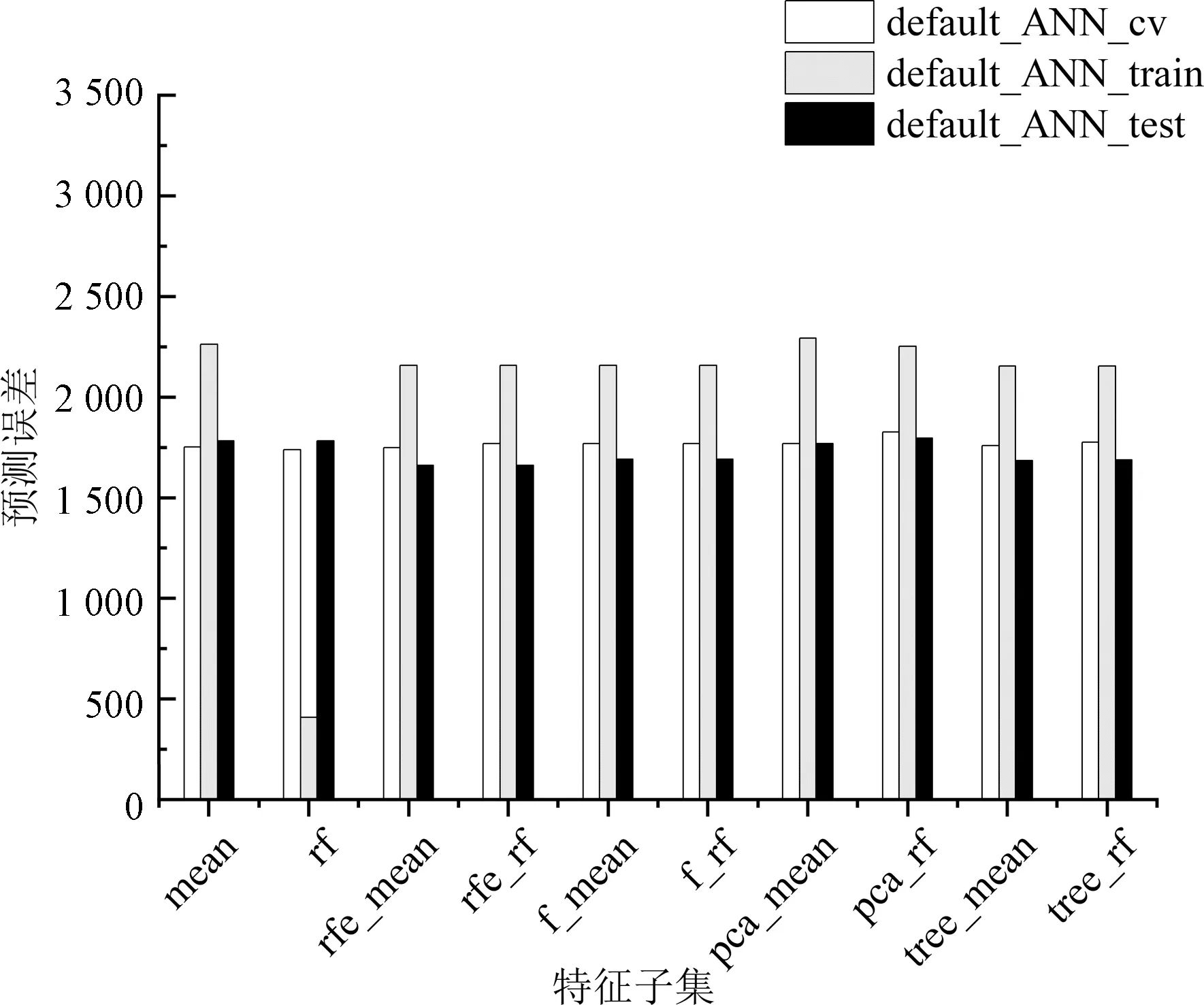
图5 默认参数下各个神经网络模型的误差

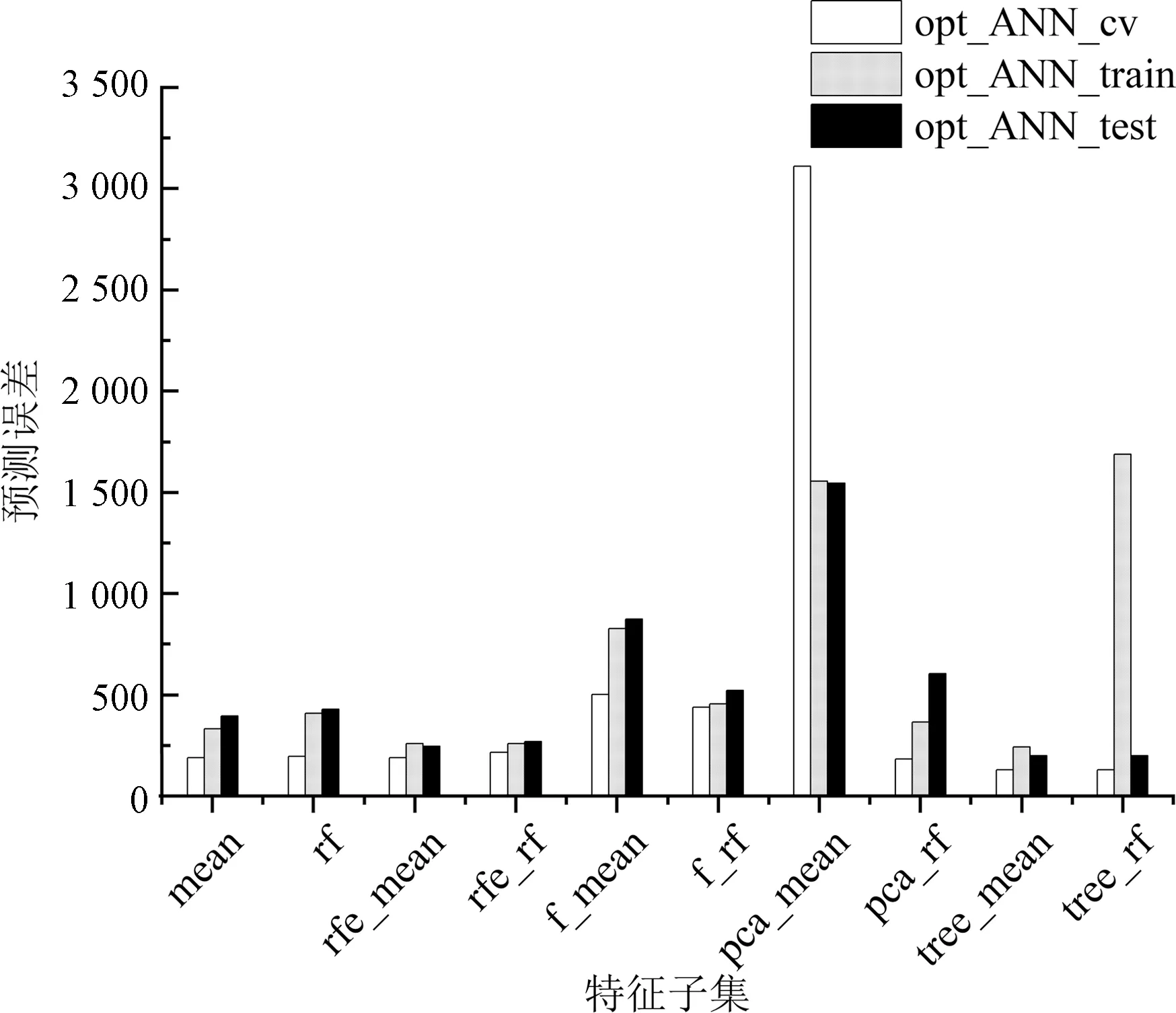
图6 优化参数后各个神经网络模型的误差

4)模型构建和评价。模型评价主要参考表3的3个误差值,其中训练和测试集误差反映模型对数据学习程度和预测能力,验证误差反映不同数据上的预测误差,也叫泛化能力或者鲁棒性。

由图1和图2可知,XGBoost的各项误差整体比神经网络低。从模型训练、测试误差和交叉验证值看,XGBoost模型能够准确地拟合数据,预测精度高,模型泛化能力好。

对比了整体算法之间的差异,还需对比最优特征子集的模型效果构建模型。选取3个误差值相对较小的模型(图7),两个模型基于最优特征子集构建的模型分别是基于树模型特征选择和随机森林填充的XGBoost模型XGB_tree_rf和基于树模型特征选择和均值填充的神经网络模型ANN_tree_mean。

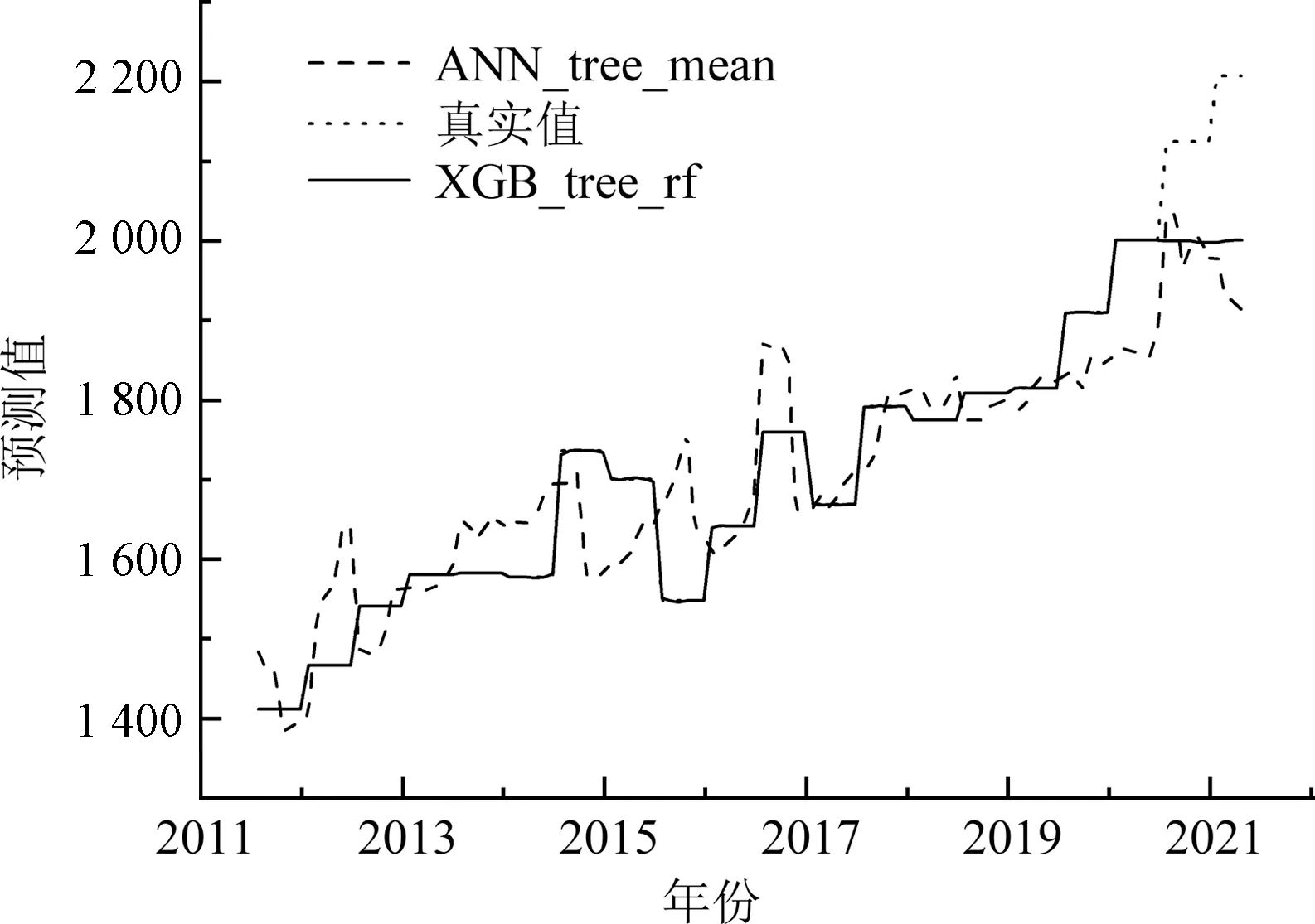
图7 最优特征子集模型预测结果

XGBoost和神经网络的预测结果如表5所示,在小数据、高纬度和数据缺失数据集上,XGBoost模型在训练集和测试集上的误差均小于10%,构建的XGBoost模型交叉验证误差小,说明模型的预测能力和泛化能力都达到实际工程中造价指数预测模型的标准。

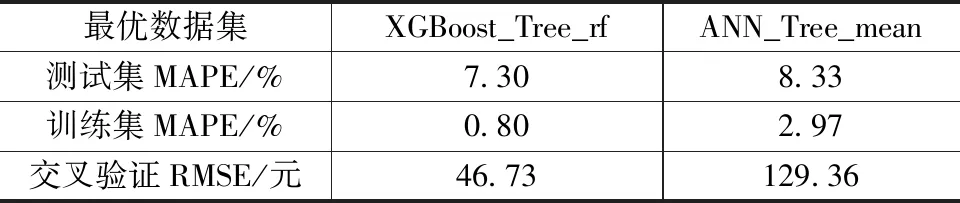
表5 算法的最优模型的模型性能对比

3 结论

通过数据填充和特征筛选得到多个数据集,以此为基础构建基于不同算法的预测模型,对比不同模型之间误差和模型稳定性,选择最优特征子集。基于参数优化后的树模型特征筛选和均值填充的XGBoost模型,测试集上的相对误差为7.30%,训练集相对误差为0.80%,交叉验证误差为46.73。因此,XGBoost作为预测造价指数的模型,数据拟合效果好,误差小,模型稳定,适合作为实际工程中造价指数预测模型。