基于垂荡运动波浪能发电PTO系统阻尼研究

平 力，尚劲光，陈茂祥，凌云凤，刘眉洁

（青岛大学物理科学学院，山东 青岛 266071）

0 引言

在当前社会背景下，人类社会对于可再生能源的需求愈来愈强［1］，海洋面积约占地球面积的71%，海洋中能开发利用的可再生能源也多种多样［2-4］。近年来，随着海洋能开发技术不断完善，国内外推出了大量政策鼓励社会全面推广使用海洋能源［5-8］。波浪能作为海洋中一种主要的清洁能源，蕴藏量大，可再生能力强，具有较好的开发前景［9-10］。但由于波浪能的不稳定性［11］，开发合适的波浪能装置，提高系统的能量转换率，是波浪能最大化利用的关键所在。

为解决该问题，有学者提出利用振荡浮子式波浪发电分段控制策略，以发电效率为基础，结合低速和高速2 种发电模式，优化发电量，但该策略下的发电功率不稳定，发电效率低下，无法持续供电［12-13］；还有学者提出一种可应用于多浮子波浪能发电装置的液压发电系统［14］，采用蓄能器稳压控制策略，但是实际工作海域的波浪幅度不稳定，蓄能器的选型比较困难，并且成本高，不适合全面推广。

综合考虑发电总量、发电效率、系统稳定性、系统成本等因素，针对波浪能装置的垂荡运动情况建立合理的模型，并对模型进行精确求解。该模型可以适应不同的海洋场景，具有普适性，并且成本低，具有一定的推广价值。

1 波浪能装置

波浪能装置主要由浮子、振子、中轴以及能量输出（power take off，PTO）系统构成［15］，其中PTO 系统由弹簧和阻尼器组成，其模型如图1所示。

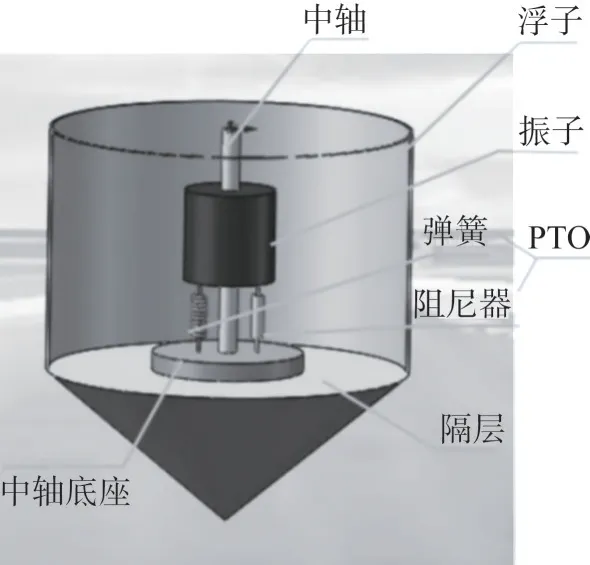
图1 波浪能装置Fig.1 Wave energy device

图1 中，波浪能装置中轴底座固定于隔层的中心位置，弹簧和直线阻尼器一端固定在振子上，一端固定在中轴底座上，振子沿中轴做往复运动。直线阻尼器的阻尼力与浮子和振子的相对速度成正比，比例系数为阻尼系数。

在实际中，阻尼系数会直接影响系统的工作效率，而阻尼系数不是定值，其值与材料、结构、阻尼模型有关［16］。阻尼系数增大，则直线阻尼器的输出阻抗逐渐小于额定负载阻抗，输出阻抗直接影响系统的低频特性。输出阻抗减小，则输出的平均功率不断增大。当增大到一定峰值时，系统转向低频工作，则直线阻尼器的阻尼系数继续增大，影响到工作效率，使输出的平均功率小幅度下滑。

选取两种特定情况下的阻尼系数，即常数PTO阻尼系数和线性PTO 阻尼系数进行研究。该装置在波浪的冲击下，浮子运动带动振子运动，两者的相对运动会驱使阻尼器做功并输出能量。波浪能的基本形式是微幅波，因此浮子在线性周期微幅波作用下会受到波浪激励力、附加质量力、辐射阻尼力和静水恢复力［17］，由于海水的黏度和旋转特性、装置内部的摩擦力等因素对能量转化影响较小，在研究中忽略不计。

2 垂荡运动模型

垂荡运动是指浮子在波浪作用下做垂直往复运动。对浮子及振子进行受力分析，得到整个系统中各部件的受力情况如图2所示。

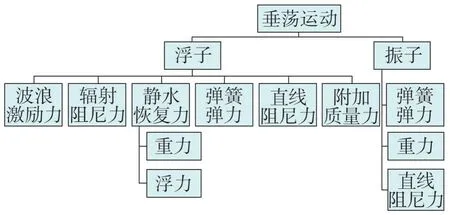
图2 垂荡运动系统受力分析Fig.2 Force analysis of vertical motion system

以浮子在静水中的平衡状态x0为零点，浮子的相对位移为x，振子的相对位移为z，浮子的相对速度为，振子的相对速度为，以沿水平面向上为正方向，得到各个力的表达式。

2.1 波浪激励力

波浪激励力，即波浪荷载，由波浪水质点与波浪能装置的相对运动所引起，是波浪对放置在海洋中的波浪能装置产生的推动力。波浪是一种随机性运动，浮子做垂荡运动时，波浪激励力为

式中：A为波浪激励力振幅；ω为波浪频率；t为波浪运动的时间。

2.2 附加质量力

波浪能装置在海水中做垂荡运动时，会引起装置周围的流体运动，因此要使装置在海水中获得一定的加速度，施加在装置上的力等于装置质量与此加速度的乘积和带动装置周围海水运动所需额外力的总和。而该额外力会对应产生一个虚拟质量，称为附加质量［18］，将此附加质量设为m0，得到附加质量力为

式中：g为重力加速度。

2.3 辐射阻尼力

波浪能装置在海水中作垂荡运动时，会带动周围水体流动，而周围水体流动会对波浪能装置的垂荡运动产生一定的阻力作用。此力与垂荡运动的速度成正比，方向相反，比例系数为辐射阻尼系数α，得到辐射阻尼力为

2.4 弹簧弹力

当振子沿中轴做往复运动时，弹簧会给振子趋向平衡位置的弹力，根据胡克定律，弹簧给振子的弹力表达式为

式中：k为弹簧的弹性系数；Δx为弹簧的伸长量。

2.5 静水恢复力

静水恢复力是指为浮子做垂荡运动时使浮子回到平衡位置的作用力，与垂荡运动过程中的浮力变化有关。静水恢复力为

式中：Ff为浮子在水中受到的浮力；m1和m2分别为浮子和振子的质量。

2.6 直线阻尼力

在该波浪能装置中，PTO 系统会将浮子在垂荡运动中克服阻尼力所做的功转化为电能。采用线性阻尼模型分析直线阻尼器的阻尼力。直线阻尼器的阻尼力与浮子和振子的相对速度成正比，其比例系数即阻尼系数为β，则直线阻尼力为

2.7 浮子与振子的运动模型

振子受力包括弹簧弹力、重力、直线阻尼力，以垂直向上为正方向，振子在波浪作用下受力情况为

浮子受力包括波浪激励力、静水恢复力、辐射阻尼力、弹簧弹力、直线阻尼力、附加质量力。因此，得出浮子和振子整个系统在海洋中的受力情况为

进一步可得振子和整个系统的运动微分方程为

3 模型的求解

3.1 初始状态求解

模型各参数值如表1所示。

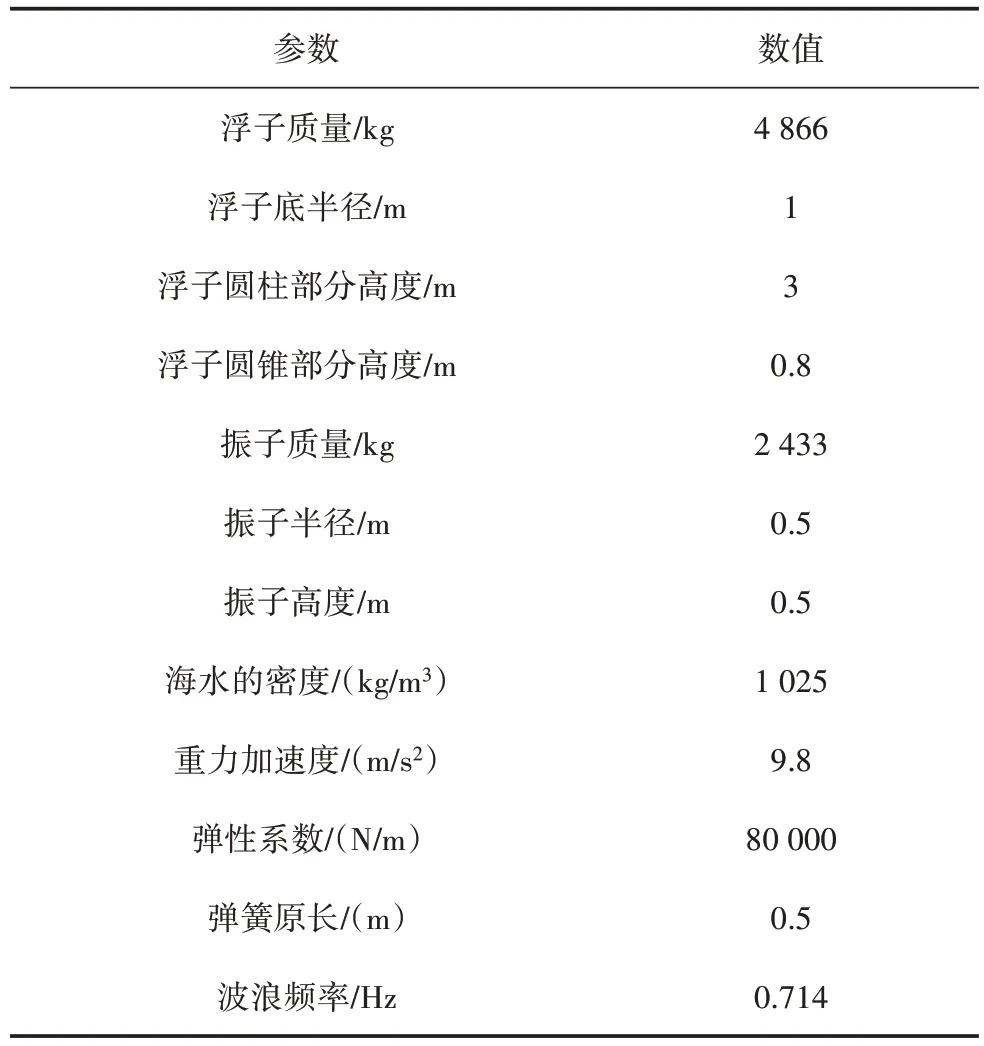
表1 模型参数Table 1 Model parameter values

在初始时刻，浮子和振子在静水中保持平衡。在平衡状态下，浮子的浸水深度大于浮子圆锥部分的高度，则浮子圆锥部分全部浸入水体中，多余的部分为圆柱浸入的体积。求得初始时刻系统的浸水深度为2.8 m，将此时水平面作为零点x0，则平衡时弹簧长度为0.202 m，振子底部与水平面相距1.798 m。

3.2 常数PTO阻尼系数

海洋波浪是在深海区由风和潮汐力共同作用的结果，潮汐力分为太阳潮汐力和月球潮汐力［19］，由于太阳对于潮汐力贡献较小，在此忽略不计。所以海波的速度基本与风速和月球引力极大值点在地表的移动速度相同。查阅文献［20］可知，一般海上风速的变化范围为10～200 m/s。

式中：ν为深水波频率；V为深水波波速；λ为深水波波长。由此推出频率变化范围为0.01～1 Hz。

本文波浪频率选取0.714 Hz。当阻尼器的阻尼系数为常量10 000 N·s/m 时，利用MATLAB 软件中ODE45 函数求解2.7 节建立的运动模型，得到浮子和振子垂荡位移、速度与时间的关系图像，如图3所示。

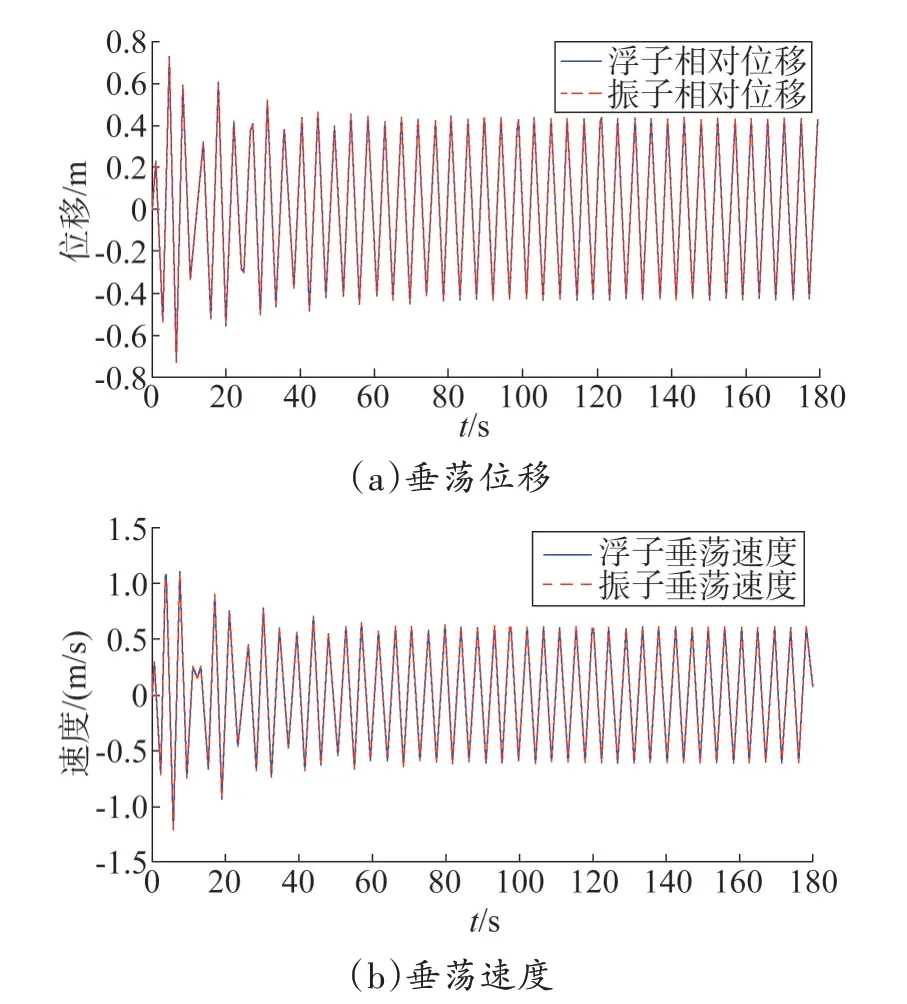
图3 常数PTO阻尼系数垂荡运动Fig.3 Constant PTO damping coefficient vertical motion

由图3 可知，当直线阻尼器采用常数阻尼系数时，浮子和振子的位移、速度趋势线吻合度较高，但位移和速度峰值均出现忽大忽小的情况，变化幅度较大；约60 s 后，整个系统处于稳定状态，位移和速度均呈周期性变化且振幅近似不变，可近似为简谐运动。系统稳定后，浮子和振子的位移、速度趋势线相似性较高。

3.3 线性PTO阻尼系数

当直线阻尼器采用线性PTO 阻尼系数时，取比例系数为10 000，幂指数为0.5，由此得到阻尼系数的表达式为

将式（11）代入式（9），利用ODE45 函数进行求解，得到此阻尼系数下浮子和振子垂荡位移、速度与时间的关系如图4 所示。

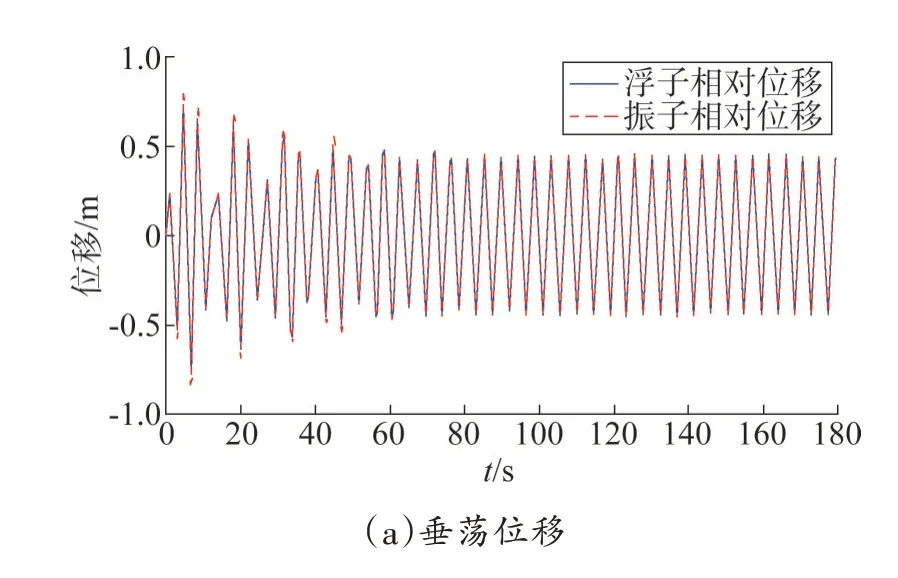
由图4 可知，当直线阻尼器采用线性阻尼系数时，浮子和振子的运动曲线几乎重合。浮子系统开始运动时浮子与振子的位移和速度振幅不稳定且无固定周期；约60 s 后，浮子和振子的运动近似呈现为简谐振动，有固定的振幅和周期。

3.4 阻尼系数对发电稳定性的影响

对比3.2 节和3.3 节计算结果可知，采用线性PTO 阻尼时，浮子和振子的垂荡运动在前60 s 内更不稳定，位移和速度幅值变化范围更大。经过60 s，系统稳定后，两种阻尼系数下，浮子和振子均近似为简谐运动状态。但当采用线性阻尼系数时，浮子与振子运动周期更短，运动频率更高，且幅值更大。波浪能转换装置的发电稳定性是指装置预热后的发电稳定性［21］，系统开启后的前60 s 可看作装置的预热时间。综合对比可知，当直线阻尼器采用线性阻尼系数时，系统的发电稳定性更好。

3.5 阻尼系数对功率的影响

在波浪的作用下，浮子与振子的相对运动会驱动阻尼器做功，并能将所做的功作为能量输出。功率的表达式为

由3.2节和3.3节分析可知，系统稳定后，浮子和振子的运动可以近似看作是简谐振动。则系统平均输出功率为

3.5.1 常数PTO阻尼对功率的影响

直线阻尼器采用常数阻尼时，联立运动模型以及平均输出功率表达式，利用变步长搜索法，绘制出平均输出功率随阻尼系数变化曲线，如图5所示。

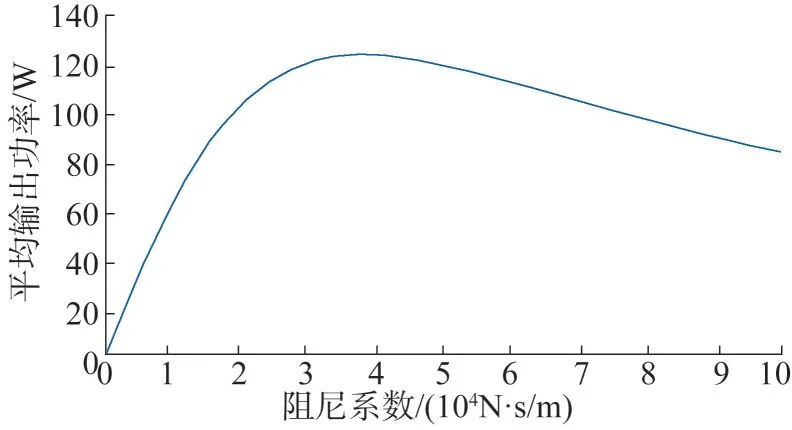
图5 常数PTO阻尼下平均输出功率曲线Fig.5 Average output power curve at constant PTO damping

由图5 可知，随着阻尼系数的增加，平均输出功率呈现出上升趋势且增长速度较快；当阻尼系数达到2.93×104N·s/m 时，增长较为缓慢且图像斜率近似为零；而在阻尼系数达到3.79×104N·s/m时，平均输出功率呈现下降趋势，但下降的速度较为缓慢。平均输出功率最大时对应的阻尼系数范围为30 000～40 000 N·s/m。缩小阻尼系数区间后，利用变步长搜索法进行精确求解，最终求得最大平均输出功率为124.20 W，对应的阻尼系数为37 940 N·s/m。

将该阻尼系数代入式（13），绘制出每时刻对应的输出功率如图6所示。

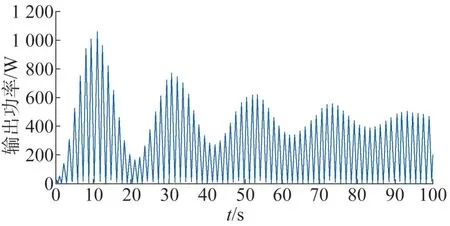
图6 最优常数阻尼系数下的输出功率Fig.6 Output power at optimal constant damping coefficient

3.5.2 线性PTO阻尼对功率的影响

直线阻尼器采用线性阻尼时，得到阻尼系数的表达式为

式中：a为比例系数，a∈［0，100 000］；b为幂指数，b∈［0，1］。

将式（14）代入式（9）与式（13），利用变步长搜索法绘制出平均输出功率随a与b的变化曲线，如图7所示。

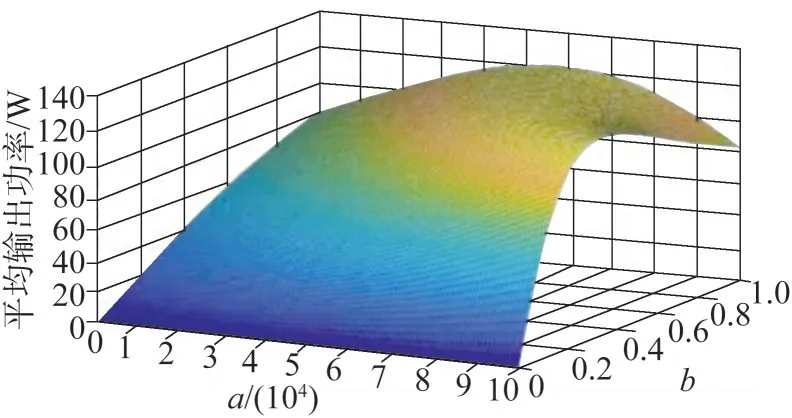
图7 线性PTO阻尼下平均输出功率曲线Fig.7 Average output power curve at linear PTO damping

由图7 可知，随着两个参数的增加，平均输出功率呈现出大幅度上升，而后上升速度减慢并逐渐趋于0，最后缓慢下降的趋势。缩小两个参数取值区间后，利用变步长搜索法进行精确求解，最终求得最大平均输出功率为124.22 W，对应的比例系数a和幂指数b分别为97 000和0.4。

将这两个参数代入式（13），求解最优阻尼系数为46 025 N·s/m，并绘制出每时刻对应的输出功率如图8所示。

4 结束语

建立波浪能发电装置模型，采用ODE45 函数求解数值解，研究了该装置在海洋中做垂荡运动的发电性能。在此基础上，进一步求解该装置的最优阻尼系数和最大发电功率，研究了该波浪能装置的最优工作参数，并采用变步长搜索法进行积分。通过代入实际数值对模型进行验证发现，该模型与实际情况拟合较好。因此，所建立的模型具有一定的可行性和研究价值。