求解多重线性系统的预条件张量分裂Gauss-Seidel迭代法
种园园,吕长青
(枣庄学院 数学与统计学院,山东 枣庄 277160)
0 引言
在数据挖掘、偏微分方程数值解和工程计算等科学领域,许多问题的计算往往归结为求解多重线性系统[1-5]
Axm-1=b,
(1)
其中:张量A∈R[m,n],A=(ai1i2…im),ik=1,2,…,n,k=1,2,3,…,m。已知向量b∈Rn,未知向量x∈Rn利用分裂法求解多重线性系统(1)时,由于储存和计算量大以及迭代法对系数张量谱分布的依赖,所以经常面临着收敛慢或不收敛等问题。为了解决这些问题,通常将迭代张量进行一次预处理后再用分裂迭代法求解。
LI 等[6]提出了预处理多重线性系统PAxm-1=Pb,并证明它与多重线性系统(1)同解,文中还提出了预条件子P=I+Sα,其中
经过正则分裂PA=εp-Fp,提出了如下预处理张量分裂的迭代算法:
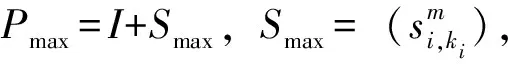
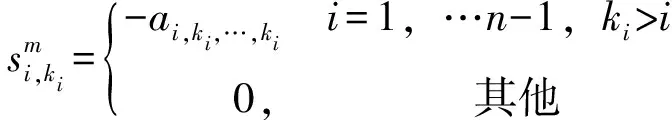
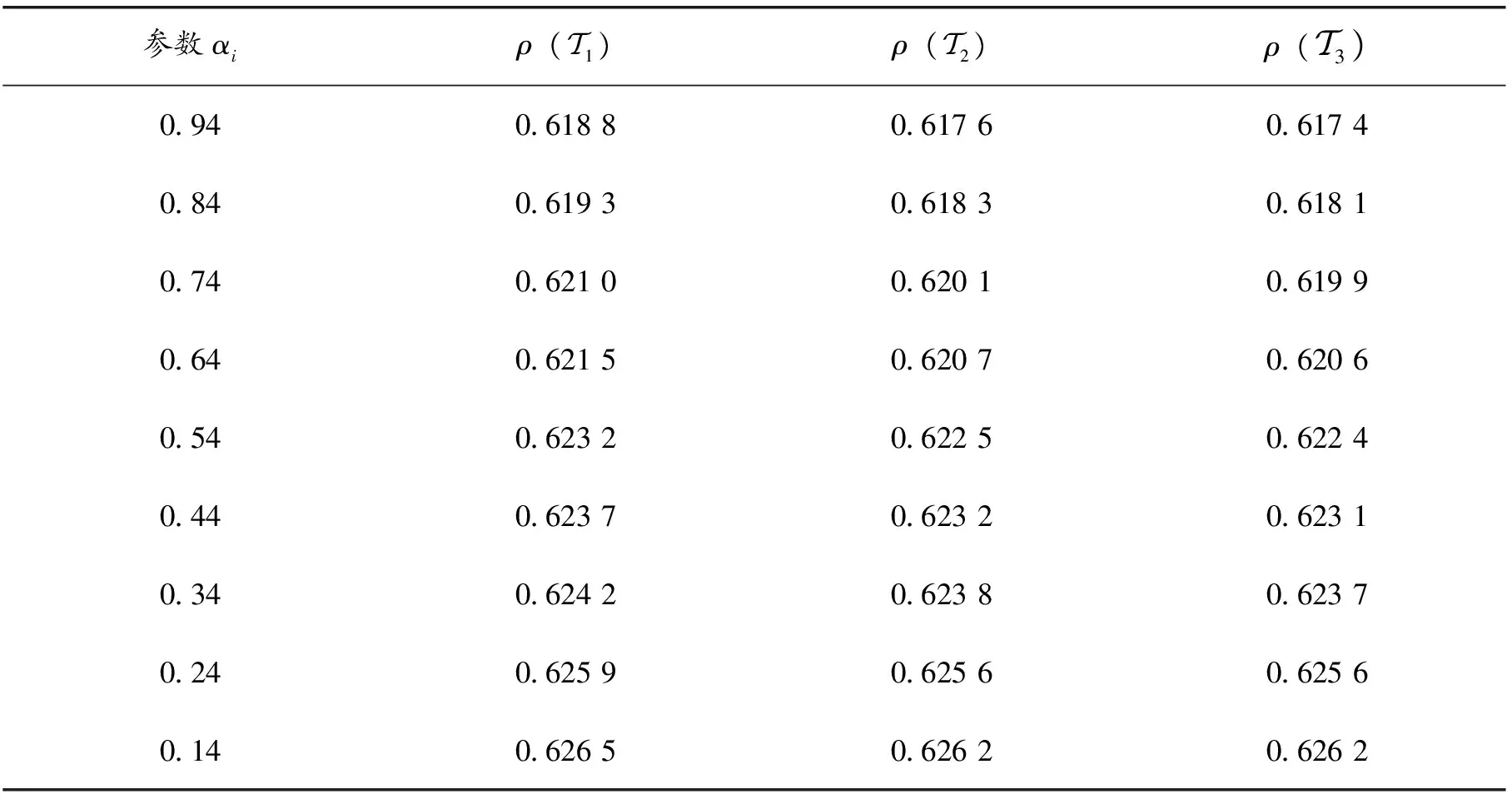
其中:ki=min{j|max|aij…j|,i ZHANG 等[8]根据A的优矩阵[9]构造了一个新的预条件子I+Gα,其中 同时提出了预处理Jacobi迭代法,并证明了所提出预处理迭代方法的收敛性。论文针对张量的一般张量分裂,提出基于3种分裂方式的Gauss-Seidel迭代法,证明了收敛性并通过数值实验验证了它们的有效性。 设A∈R[m,n]是强M-张量,为了符号的简单和不失一般性,假定A的对角线元素是1。考虑一般分裂A=I-L-U-F,这里I=IIm,L=LIm,U=UIm,Im是单位张量,-L、-U分别是优矩阵M(A)的严格下三角矩阵和严格上三角矩阵,其中M(A)∈R[2,n],(M(A))ij= (2) 其中:参数αi∈[0,1],i=1,2,…,n,且αn=0。 考虑以下三种分裂方式: (3) 基于上述3种分裂方式,得到相应的Gauss-Seidel迭代张量。 Tk=M(εk)-1Fk,k=1,2,3。 (4) 分别用O、O、0表示零矩阵、零张量、零向量。 定义1[10]设A∈R[m,n],若A的所有非主对角线元素是非正的,则称A为Z-张量。 定义2[11]设A为Z-张量,且A满足A=ηI-B,其中B为非负张量,η为正实数。若η≥ρ(B),则称A为M-张量。若η>ρ(B)则称A为强M-张量,这里ρ(B)为张量B的谱半径。 定义3[12-13]设A,ε,F∈R[m,n]若ε是左可逆张量,则称A=ε-F是A的一个分裂。 (i)若ε是左可逆张量,且M(ε)-1≥O,F≥O,则称A=ε-F是A的一个正则分裂。 (ii)若ε是左可逆张量,且M(ε)-1≥O,M(ε)-1F≥O,则称A=ε-F是A的一个弱正则分裂。 (iii)若ρ(M(ε)-1F)<1,则称A=ε-F是收敛的分裂。 定义4[14]设矩阵A∈Rn×n,且A=sI-B,s>0,B≥O,若s>ρ(B),则称矩阵A为非奇异M矩阵,这里ρ(B)为矩阵B的谱半径。 引理1[15]若矩阵A为非奇异M矩阵,则A-1≥O。 引理2[12]设A∈R[m,n]是Z-张量,则下列条件等价: (i)A是强M-张量; (ii)存在一个实向量x>0,使得Axm-1>0; (iii)所有A的正则(弱正则)分裂都收敛。 当(i1,i2,…,im)≠(j,…,j)时,因为A∈R[m,n]是强M-张量,所以ai1i2…im≤0。又由于αi∈[0,1],i=1,2,…,n且αn=0,可知: (i)若i1=1,则bi1i2…im=ai1i2…im≤0; (ii)若i1=n,则bi1i2…im=ai1i2…im-αi1ai1i2…im=(1-αi1)ai1i2…im≤0; (iii)若i1≠1,n,则bi1i2…im=ai1i2…im-αi1ai1n…nani2…im≤0。 引理4[6]设A∈R[m,n]是强M-张量,若A=ε1-F1=ε2-F2是2个(弱)正则分裂,且F2≥F1≠O,则ρ(M(ε2)-1F2)≥ρ(M(ε1)-1F1)。 由引理3,可以得收敛定理1。 定理1 设A∈R[m,n]是强M-张量,则对任意的αi∈[0,1],i=1,2,…,n且αn=0,(3)式中的(Ⅰ)和(Ⅱ)均是收敛的分裂。 定理2 已知A∈R[m,n]是强M-张量,当αi∈[0,1],αn=0且1-αiain…nani…i>0,i=1,2,…,n时,式(3)中的(Ⅲ)是收敛的分裂。 证明M(ε3)=I-L+Lα-Dα=I-L-(Dα-Lα),由于αn=0,则 根据引理4可以得到如下比较定理。 定理3 已知A∈R[m,n]是强M-张量,当αi∈[0,1],αn=0且1-αiain…nani…i>0,i=1,2,…,n时,ρ(T1)≥ρ(T2)≥ρ(T3),其中 Tk=M(εk)-1Fk,k=1,2,3。 由式(3),通过比较得到F1≥F2≥F3≠O,则ρ(M(ε1)-1F1)≥ρ(M(ε2)-1F2)≥ρ(M(ε3)-1F3),即ρ(T1)≥ρ(T2)≥ρ(T3)。 这里将给出2个数值算例来验证的上述理论结果,以下2个例题均采用算法Ⅰ计算迭代张量的谱半径。 算法Ⅰ 输入x0,最大迭代次数K,容许误差ε=10-6,迭代张量T; k=1; p1=min(p0); p2=max(p0); ε0=p2-p1; ifε0≤ε; break; end k=k+1; y0=y1; end 输出迭代张量T的谱半径p。 例1[7]设张量 第一组取α1=α2=0.9,计算结果如下: 第二组取α1=0.9,α2=0.4,计算结果如下: 第三组取α1=0.2,α2=0.8,计算结果如下: 例1结果表明,当变化参数αi(i=1,2)取值时,文中所给3种分裂方式都是收敛的,且每组取值结果均满足ρ(T1)≥ρ(T2)≥ρ(T3)。与文献[8]中的结果相比较,第二组和第三组所计算出的谱半径均小于ρ(Tmax)=0.338 6,收敛速度更快。 例2 设张量=A=I-B,其中I为单位张量,张量B=(bi1i2i3)∈R[3,5],i1,i2,i3=1,2,3,4,5,其中 表1 参数αi与对应迭代张量的谱半径 例2结果表明,当变化参数αi取值时,3种分裂方式也都是收敛的,且每组结果均满足ρ(T1)≥ρ(T2)≥ρ(T3)。同时还可以发现ρ(Tk)(k=1,2,3)随参数αi变大而减小,即参数αi越大,三种分裂方式的收敛速度均是越快。1 收敛性分析

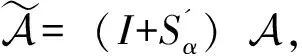
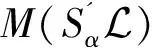

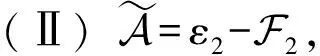
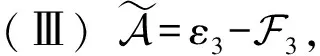
1.1 基本定义和基本引理
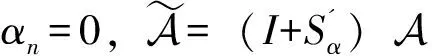
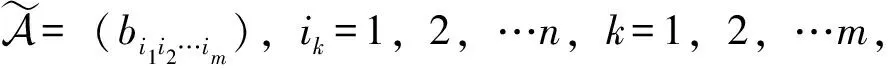

1.2 收敛定理
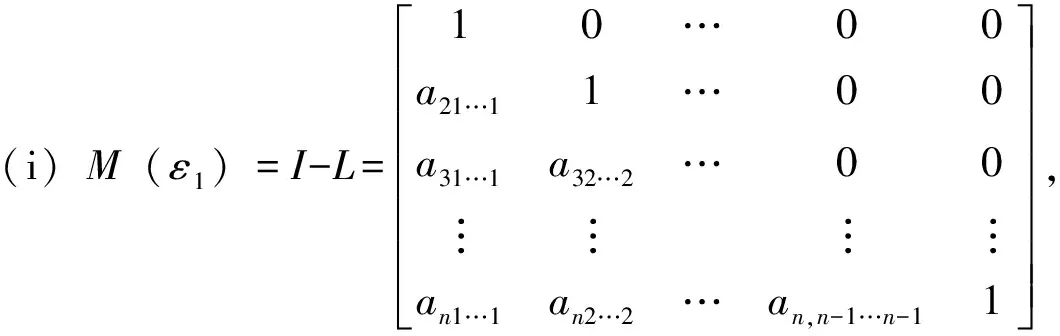
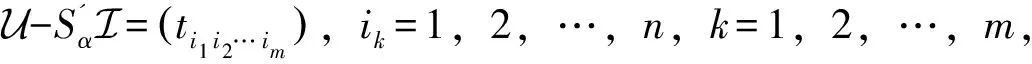
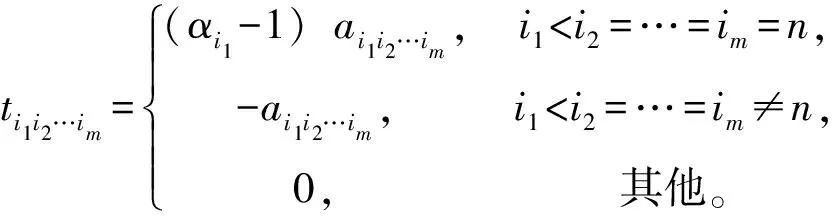

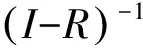
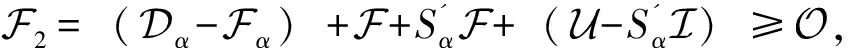

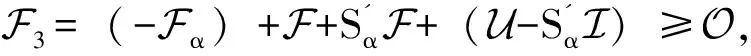
1.3 比较定理

2 数值验证





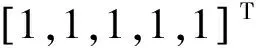
3 总结