混合式现场变形指纹的校正方法研究
高 畅,沙良潇,赵雪珺,包 清,3
(1.上海市公安局刑事侦查总队,上海 200083; 2.上海市刑事科学技术研究院 上海市现场物证重点实验室,上海 200083; 3.上海理工大学,上海 200093)
在各类刑事案件的现场勘查过程中,指纹一直是痕迹物证的重要组成部分,能够起到明确案件性质、锁定嫌疑人等诸多关键作用。 在指纹检索比对过程中,变形指纹会产生不利影响,使得正确的比中结果在候选列表中排名靠后,甚至会不出现在自动指纹识别系统(automatic fingerprint identification system,AFIS)反馈的候选列表中。
对于变形指纹的校正,国内外相关研究学者已有了很多研究。 国内的研究主要包括陶桂兰等[1]报道的在特定约束条件下,利用Photoshop 软件的自由变换功能对图像进行校正并比中嫌疑人的案例。但该方法依赖人工操作,不具备模式特征且不易推广,案例数量过少,说服力不足。 曹轶超等[2]提出了使用Matlab 软件通过预制变形模板和人工选取网格参考点相结合的方法多项式拟合校正,该方法的校正效果受制于人工对特征点的选取,高阶数对取点和计算量的要求较高,低阶数的拟合效果可能不尽理想。 仲伟波等[3]提出了利用指纹拓扑模式自动匹配和识别指纹,该方法对变形指纹鲁棒性强,匹配率达到近60%,但该匹配率仍然较低,且与现有的指纹识别系统不兼容。 栗赫遥等[4]提出了一种自适应的渐变曲率校正方法,该方法对于曲率半径发生变化的曲面有很好的效果,但该方法只适用于圆柱面,对于复杂曲面(如鸡蛋壳表面、可乐瓶表面等)则无法进行校正。 国外的研究主要包括CHEN等[5]提出的基于模糊函数相似度的检验方法,根据选取的特征参数能够给出匹配上的特征的可靠程度, 筛选出可靠特征并达到降低错误匹配的概率,但该方法要求变形指纹可被提取的特征点多,存在一些变形小的区域,现场遗留的潜在指纹往往不满足上述条件。 ROSS 等[6]以及LIN 等[7]提出了基于薄板样条函数(thin plate spline,TPS)对变形指纹进行校正的方法,该方法是一种指纹纹线的匹配而不仅仅是特征点的匹配,但该方法要取得好的校正效果,一是需要多张同枚指纹的变形图像,但在现场勘查中,遗留单枚变形指纹的情况更为常见;二是需要指纹图像能够清晰连贯高反差地从承痕体中区别出来,而在现场勘查中各种背景干扰、附着物干扰、纹线反映不清晰不连贯等情况也使得该方法过于理想化。 SENIOR 等[8]选择另辟蹊径,将指纹的纹线密度假设为常数,通过均衡化指纹纹线密度达到校正变形指纹的目的。该方法在校正严重变形指纹时确实能够起到很好的“视觉改善”效果,但准确性还有待商榷,比如WAN 等[9]的相关研究中明确指出了指纹纹线密度在不同的指纹区域是不同的。SI 等[10]在总结前人研究的基础上,提出了一种基于方向特征图和频率特征图的字典法校正,将待校正指纹输入模型后提取相关的特征,确定待校正指纹与字典中的哪种变形模板最为接近,再将变形模板的逆变换应用于变形指纹中,以获得校正结果。 该方 法 在FVC 2004DB1、FVC 2006DB2、Tinghua DF和NIST SD27 指纹库中均取得了优于其他校正方法的效果。 但该方法依然存在以下两个缺陷:一是为了达到更好的校正效果,需要大量增加模板数量,校正指纹的时间开销显著延长;二是该方法在应用于现场指纹库NIST SD27 时,校正效果明显下降,甚至出现一些校正结果不及原图的案例,在司法鉴定实战中表现不尽如人意。 DABOUEI 等[11]在SI 等[10]的研究启发下,利用深度卷积神经网络(deep convolutional neural network,DCNN)模型对变形指纹进行校正,该方法在模型训练完成后效果优于SI 等[10]提出的字典法,并且不存在时间开销延长的问题。 但是该方法在比较时仅仅在FVC 2004DB1 和Tinghua DF 这两个指纹库上进行了比较测试,删去了现场指纹库NIST SD27 的比较,且FVC 2004DB1和Tinghua DF 指纹库中的指纹均为捺印样本,该方法同样在的实践环节缺乏说服力。
为改善以上问题,本文提出了一种混合传统模式识别和DCNN 相结合的指纹校正技术,将传统模式识别的鲁棒性优点和DCNN 的准确性优点结合起来,对变形指纹进行校正,以提高正确比中结果在候选列表中的排位。
1 材料与方法
本文在栗赫遥等[4]与DABOUEI 等[11]研究基础上,提出了一种曲面模型传统模式识别结合DCNN的方法。 该方法结合了传统模式识别技术在现场变形指纹校正中对各种干扰因素鲁棒性强的优点,以及DCNN 网络模型在条件适当的区域校正更加准确的优点,流程说明图如图1 所示。
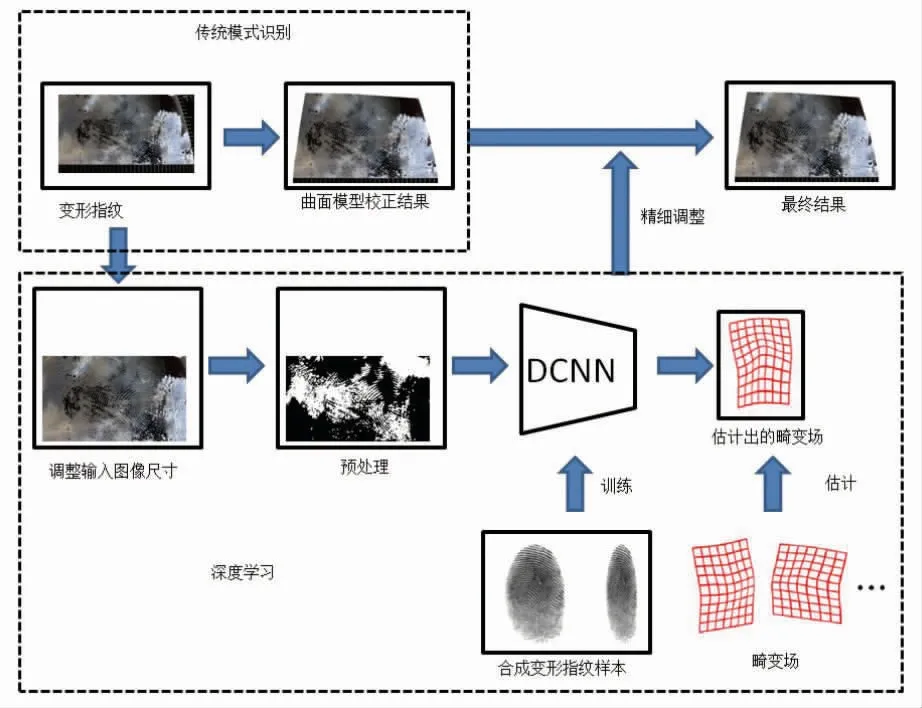
图1 校正方法总体流程图
1.1 材料
为了突出适应现场勘查实战的需求,本次实验在模拟指纹样本和测试指纹库两个环节均考虑实践需求。 一是模拟指纹样本方面。 本次实验的模拟指纹样本均为模仿遗留在现场曲面客体上的潜在指纹,经过磁性粉刷显或502 熏显,并按照相应的拍照提取要求,采用适当的光学提取方式对指纹进行拍照提取,接近现场勘查中的实际情况,存在客体背景干扰、客体表面附着物干扰、客体表面凹凸不平干扰、纹线残缺中断干扰、中心花纹模糊干扰等影响指纹图像质量的因素。 二是测试指纹库方面。 本次实验所选指纹库是上海市公安局物证鉴定中心测试指纹库,包含了超过200 万人的指纹信息,即超过2 000 万枚不同的指纹,测试得到的比中排位的变化更具有说服力。
1.2 方法
本文方法大致可分为传统模式识别模块、DCNN 模块和融合模块这三个主要模块,是一种由粗略校正到精准微调的校正方法。
1.2.1 传统模式识别模块
传统模式识别模块是依据曲面模型,将遗留有指纹的曲面客体看成是一组相似的曲线簇L1沿着L2堆叠而形成的,简化的示意图如图2 所示。 在客体表面沿着L1和L2的方向上粘贴比例尺,在不变形的条件下,比例尺上的刻度间的间隔是处处均匀的,由于曲面客体的弯曲导致客体表面存在着不同程度的投影变形,依据曲面模型和正交粘贴的比例尺可以计算出曲面任意一点的畸变场,通过逆变换后消除指纹的变形。
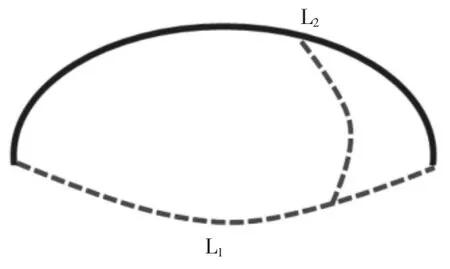
图2 曲面模型示意图
首先,要计算出在L1处的横向畸变场,具体方法与栗赫遥等[4]提出的校正方法相类似。 通过标尺刻度宽度与标尺刻度间隔构造一个衡量弯曲程度的数组,构造方法如下:
通过数组cn,可以估计出在L1上投影畸变程度最轻的位置t,估算的具体方法如下:
式(2)中t的集合为候选集合,候选集合由不小于cn中最大元素的99%对应的元素位置组成。balance( )函数的返回值为变量及其倒数的最小值,根据式(2)求解得到的t,即为L1上投影畸变程度最轻处。 下一步是使用一个曲率半径为常数的圆弧与数组按照下式进行最佳匹配:
match()函数是指以t位置处为圆弧的顶点进行的以固定曲率半径进行匹配,则是欧氏距离的计算方法。 为了适应各种复杂曲面的匹配,在式(3)的基础上还需要进行曲率半径的二阶补偿,如式(4)所示:
至此,L1处离散的横向畸变场求解结束,下一步需要将离散的横向畸变场转变为连续的结果,使得L1处任意一点的横向畸变场可以被确定。 其示意图如图3 所示,转化过程可按照式(5)进行:
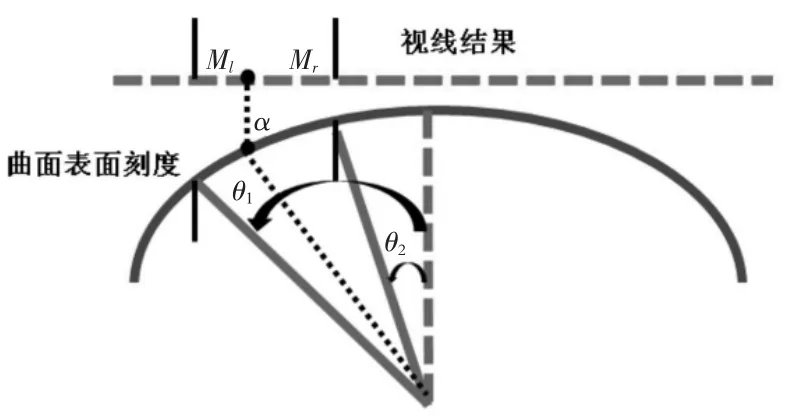
图3 畸变场连续化示意图
经过连续化处理后,L1处任意一点α 的横向畸变场βh(α)的计算结果为:
式(6)中的参数θx是依据式(5)计算得到的调和转角,其余参数可参见式(4)。需要指出的是,式(3)~(6)需要在t位置处两侧分别计算匹配。 采用上述方法同样可以计算得到L2处的纵向畸变场βv(α),具体过程不再赘述。
在获取到L1处的横向畸变场及L2处的纵向畸变场的基础上,为了克服栗赫遥等[4]所提方法只适用于柱面客体的缺陷,需要将畸变场的计算推广至曲面上的任意一点。 先将L1处的横向畸变场推广至曲面上任意一点的横向畸变场,将曲面看成是一组与L1相似的曲线簇在曲线L2上的堆叠,对曲面上任意一点的横向畸变场βh(τ)进行近似估计,具体如式(7)所示:
式(7)中的(x,y)是曲面上任意一点的坐标,函数是依据L2和t的关系,估计得到该点所在水平线的横向畸变场和L1处横向畸变场对应关系的变换,示意图如图4 所示。 其中:图4(a)中的实线表示不同水平位置的曲面弯曲可以被近似地认为是一组相似的曲线簇,存在诸如C1-D2,C2-D2,C3-D3的相似关系;图4(b)不同水平位置与L1处横向畸变场的相似比为r2/r1,其中r2表示该点水平线在通过t的垂线和L2之间的距离,r1表示L1处水平线在通过t的垂线和L2之间的距离。
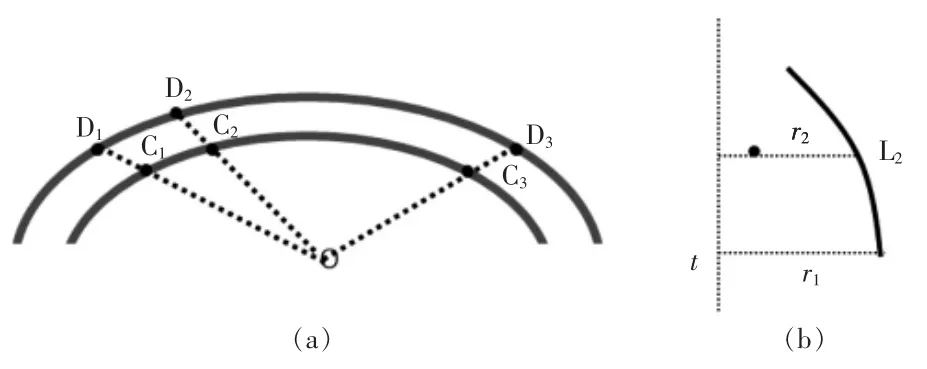
图4 transformh()函数示意图
现还需将L2处的纵向畸变场推广至曲面上任意一点的纵向畸变场,依据曲面模型,当L1处的横向畸变场为曲率半径固定的圆弧时,客体曲面可以看成L2沿着L1旋转而成,曲面上任意一点对应转角的纵向畸变场均与L2相同。 当L1处的曲率半径不固定时,曲面上任意一点对应转角的纵向畸变场βh(τ)均可近似地估计为L2拉伸变换后的结果,计算方法如式(8)所示:
式(8)中的L1和R分别表示L1以及曲率半径固定为R的横向畸变场,k则是式(9)中的拉伸比例系数,(x,y)是曲面上任意一点的坐标,transformv()函数则是由L2处的纵向畸变场βv(α)通过拉伸变换得到的纵向畸变场,纵向畸变场的变换示意图如图5所示。 其中:图5(a)中的实线表示L1处的横向畸变场,虚线表示虚拟的曲率半径不变的圆弧对应的横向畸变场,r1表示任意点到L1畸变场的距离,r2表示任意点到L2虚拟曲线的距离,r1/r2即为k;图5(b)中的虚线表示L2对应的纵向畸变场,实线表示L2拉伸变换后得到的纵向畸变场L2′,比例系数即为k。
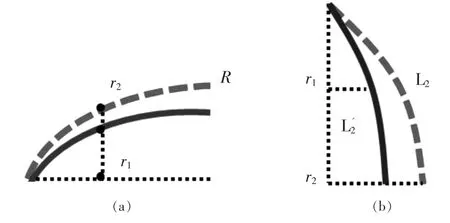
图5 βv(τ)计算示意图
1.2.2 DCNN 模块
本文所提DCNN 模块在训练集的选取、参数的设置以及训练的具体方法上均与DABOUEI 等[11]所提的方法相一致。 从BioCOP 2013 数据库中选择1033 枚正常指纹,按照从Tinghua DF 数据库中的两个主要变形因素对每一枚正常指纹生成400 枚变形指纹,并对DCNN 模块进行训练。 网络的训练次数为40 次,每次进行6 265 次的迭代,批量学习样本数为64,优化方法为Adam,其中beta为0.5,学习率为10-4。输入图像大小为256×256×1。 每层采用的方法为卷积(Conv)、数据批标准化(batch normalization,BN)、修正线性激活函数(ReLU)和最大池化(max-pooling,MP),最大值池化的步长为2。 需要指出不同的是,本文的模拟样本为模拟现场遗留的潜在指纹, 而不是捺印的高反差灰度图像,故需要对指纹图像进行预处理,将其转化为DCNN 需求的图像再进行处理,网络的具体结构参见表1。其中:方法有卷积(Conv),数据BN,修正线性激活函数(ReLU),MP,最大池化的窗口2×2,池化步长为2;所有的卷积步长为1。
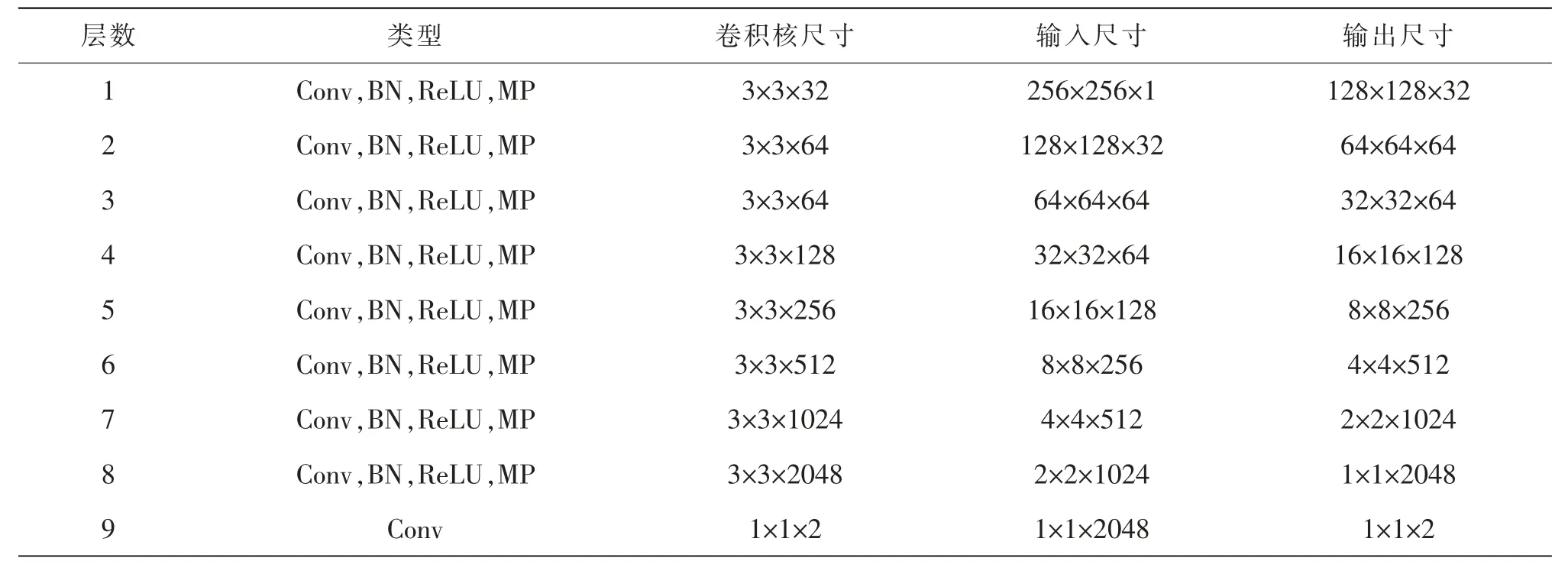
表1 DCNN 结构参数
1.2.3 综合应用模块
传统模块和DCNN 模块各有优点,传统模块鲁棒性强且对图像要求低,可应对各种干扰,DCNN 模块的优点则是准确性高,当指纹的小块区域干扰少且与训练集合类似时,可取得更为准确的校正效果。
DCNN 模块输入的图像大小均为256×256 像素,首先需要将DCNN 输入的图像切割成32×32 像素的小块,并且将32×32像素的小块与利用传统方法校正和DCNN 校正后的相同区域对应起来,示意图如图6 所示。

图6 DCNN 模块和传统模块分割32×32 方格对应关系示意图
综合应用的评判指标是两种校正方法结果对应分割方格的相似性。 当相似度低时,意味着DCNN 模块受到的干扰大且效果不佳,适合采用传统模块校正;反之则说明DCNN 模块校正结果适用性强,适合采用DCNN 模块对传统模块结果进一步优化。 相似度的计算方法如式(10)所示:

图7 相似度计算示意图
当相似度低于阈值时,传统模块对该分割方格校正的结果即为最终结果;反之,还需要结合DCNN 模块结果在保证分割方格外轮廓的同时,对内部像素点的分布进行一次调整,内部调整方法遵循式(11):
式(11)中(x1,y1)′ ′ 的代表融合了DCNN 结果后,内部调整后对应点的坐标,(x1,y1)代表传统方法校正后点的坐标,函数是指将传统方法结果的分割方格对应到相同序数关系的DCNN 结果的分割方格。函数transformco()则是在确保坐标系内相对位置关系不变的约束条件下,将transformob()计算得到的点再映射回传统方法结果的分割方格中,示意图如图8 所示。 其中:图8(a)中的蓝色虚线表示传统方法校正后对应的32×32 像素分割方格的外轮廓,红色小方格代表每一个像素点的畸变场,黑色实心方格表示精细调整前的初始点位置,黑色虚线方格表示经过了transformco()、transformob()函数映射后的调整后位置;图8(b)中的蓝色虚线表示DCNN 方法校正后对应的32×32 像素分割方格的外轮廓,红色小方格代表每一个像素点的畸变场,黑色实心方格表示初始位置由transformco()函数映射得到的对应位置。
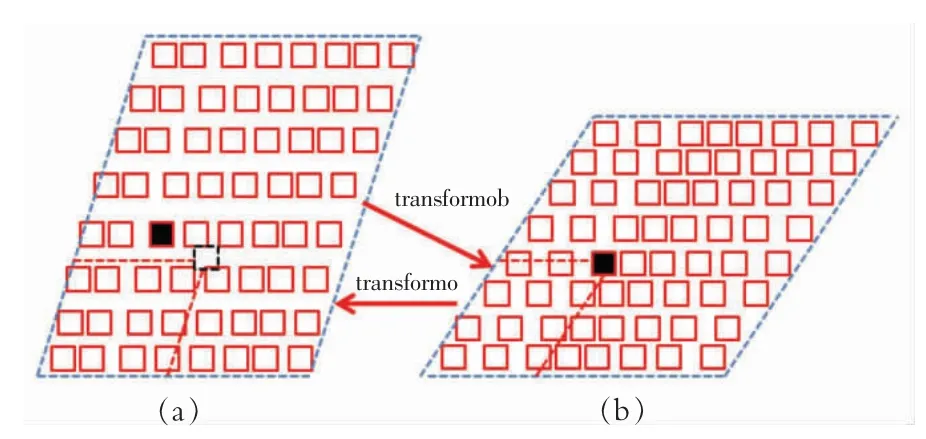
图8 精细调整示意图
由于邻近畸变场存在相似性,精细调整的强度应当与邻近畸变场参与精细调整的数量正相关,因此需要对式(11)修正如下:
其中,(x1″ ,y1″)为调整的最终结果,ωi为取决于邻近32×32 像素分割方格畸变场的系数,示意图如图9 所示。其中,中间的方格是待处理的32×32 像素分割方格,相邻的其他方格代表着相邻的32×32 像素分割方格。 图9(a)表示邻近32×32 像素分割方格满足相似度阈值的个数为1,ω1=0.25。 图9(b)表示邻近32×32 像素分割方格满足相似度阈值的个数为2,ω2=0.5。图9(c)表示邻近32×32 像素分割方格满足相似度阈值的个数为3,ω3=0.75。 图9(d)表示邻近32×32 像素分割方格满足相似度阈值的个数为4,ω4=1。
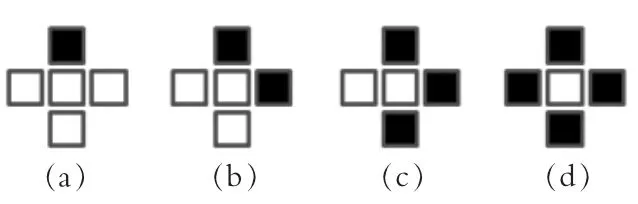
图9 系数调节示意图
2 结果
为量化本文方法的校正效果,使用了本文方法与DABOUEI 等[11]所提方法对40 枚模拟现场变形潜在指纹进行校正后,在上海市公安局物证鉴定中心测试指纹库中进行检索比对,比较未经校正的图像、两种不同方法校正的图像在比中排名上的变化如表2 所示。实验将该结果绘制成累积匹配特性曲线(cumulative matching characteristic,CMC),具 体如图10 所示,其中排名标记为“1#、2#、3#、5#、10#、15#、20#、25#、35#、40#、45#、50#、100#、200#”。
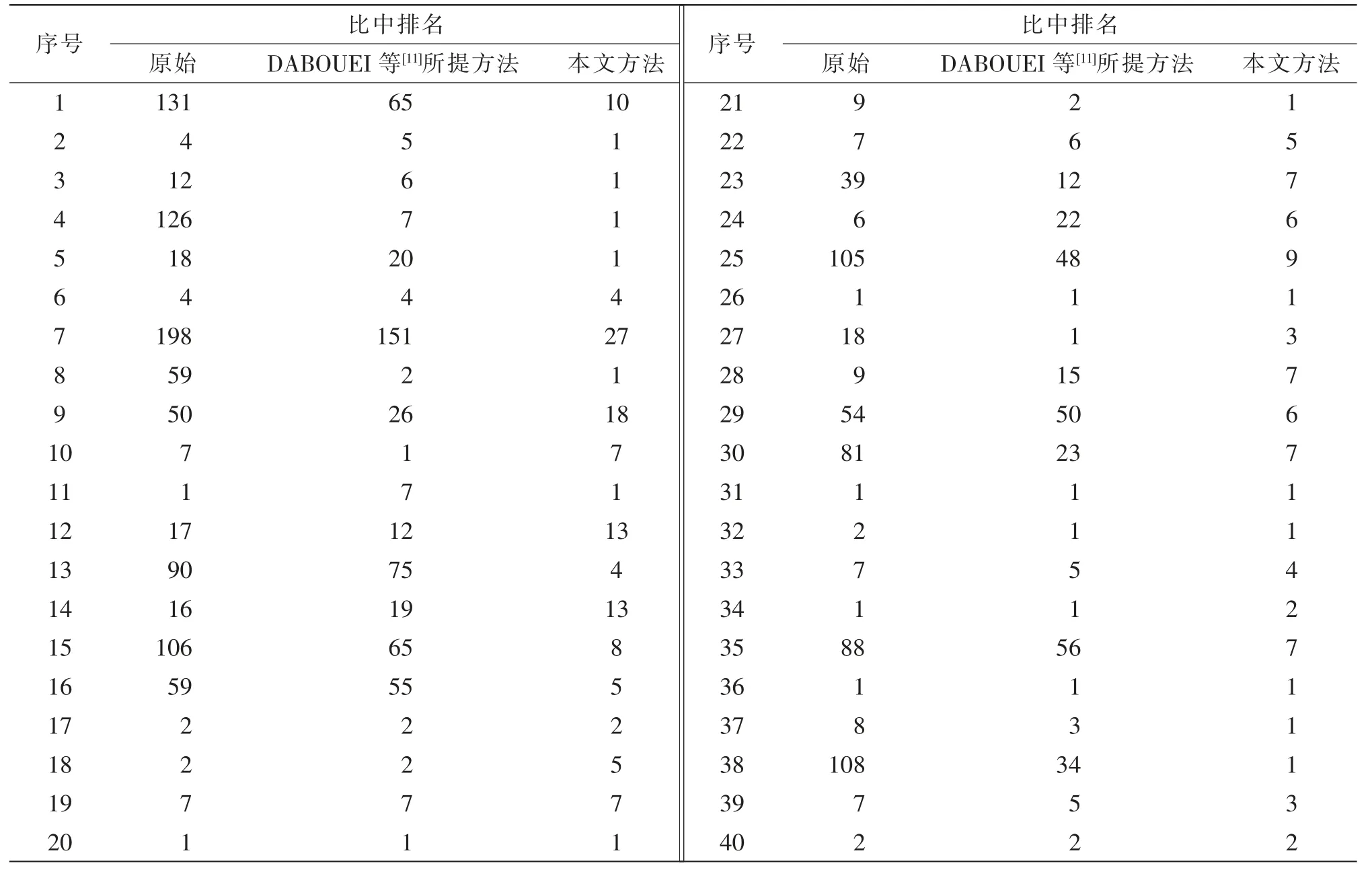
表2 同枚指纹在不同校对方法中的比中排名结果

图10 不同校对方法的CMC 结果比较
根据以上结果可以发现:(1)两种方法的处理结果均对比中率有提升作用。 (2)本文方法对比中率的提升优于DABOUEI 等[11]所提方法。 (3)本文方法对低质量变形指纹的校正有显著优势,原始图片中50 名内的比中率为70%,经过DABOUEI 等[11]所提方法校正后可提升到85%,而本文方法可提高到100%。 通常人工复核的指纹就是候选列表中的前50 名,故候选列表中前50 名能否比中对司法鉴定有重大意义。
当指纹纹线连贯且特征点数量多时,变形对排位的影响较小,本文方法显著优于DABOUEI 等[11]所提方法的示例如图11~13 所示。 多种在现场勘查过程中常见的干扰因素均会显著降低指纹图像的质量。 而在参考文献中训练样本和测试样本为捺印样本,该样本过于理想化,使用现场指纹测试时往往不能取得良好的效果。
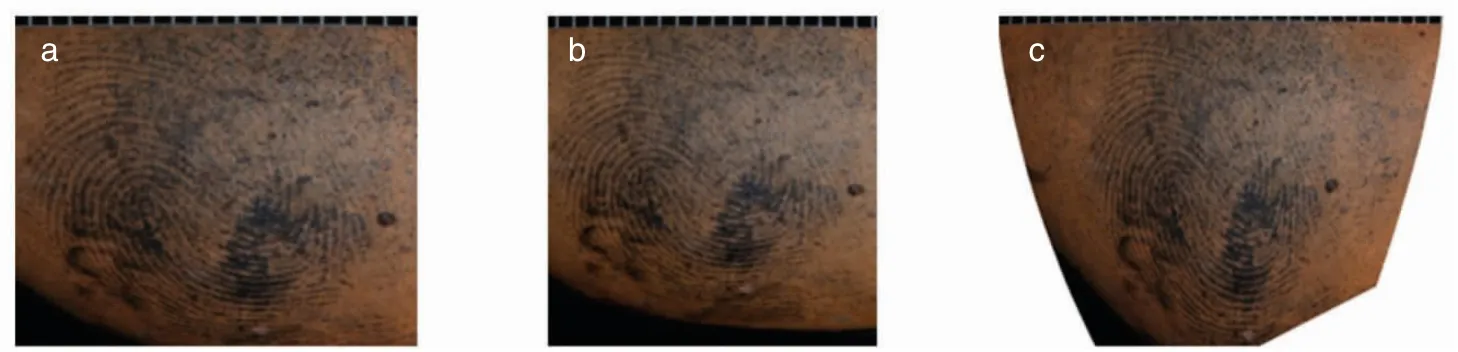
图11 同枚指纹的比较结果(严重的非线性形变以及表面的其他附着物降低了图片质量)

图12 同枚指纹的比较结果(红圈处的纹线重叠和整体纹线浅淡降低了图片质量)
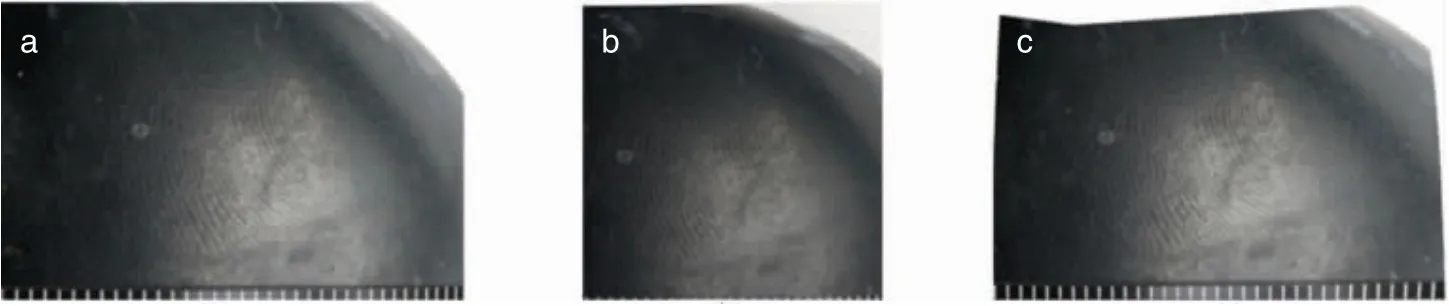
图13 同枚指纹的比较结果(承痕体凹凸起伏的表面降低了图片质量)
3 结 论
指纹变形导致的AFIS 识别准确率下降的问题一直是指纹检验中的难点。 在现场勘查中,曲面客体上变形指纹是一种典型的相对常见而又利用率低的疑难痕迹物证。 现有研究方法对现场变形指纹的校正均不能取得良好的效果,本文提出了一种混合式的校正方法,兼顾了传统模式识别方法的鲁棒性和DCNN 模块的准确性,本文方法主要的优势有两点:(1)不需要参考指纹,单张变形指纹图片即可校正。 (2)方法在司法鉴定内适用性强,对现场勘查中提取到的实际变形指纹存在的各种干扰均有着很强的鲁棒性,校正效果好,尤其是低质量变形指纹图像校正效果显著优于未校正图像及比较方法的校正结果。 本文介绍的方法能够稳定可靠地校正现场曲面客体上提取到的各种变形指纹,为提高现场勘查中疑难痕迹物证的利用率提供了新的突破口。

