基于Max-plus代数法的市域铁路快慢车运行特性
郑 翔 徐行方 刘 薇 鲁 玉
(1.广州地铁设计研究院股份有限公司, 510010, 广州; 2.同济大学道路与交通工程教育部重点实验室, 201804, 上海; 3.上海市轨道交通结构耐久与系统安全重点实验室, 201804, 上海; 4.国家开发银行苏州市分行, 215128, 苏州∥第一作者, 高级工程师)
市域铁路是连接市区与郊区、周围卫星城镇及都市圈的轨道交通线路,具有运量大、速度快、站距长(设站少)等特点。采用高密度、周期化的快慢车运行模式可以减少乘客的出行时间,满足多元化、快速化的出行需求。由于快慢车模式中采用快车越行、慢车避让的行车模式,一旦出现晚点,列车恢复运行的调整难度随之增大。这就要求列车运行图在计划阶段就能保证列车运行系统的鲁棒性,提高列车运行图的抗干扰能力。文献[1]利用改进遗传算法优化城市轨道交通列车运行图的鲁棒性,但其未对快慢车行车模式进行研究。文献[2]提出2种可恢复鲁棒性的优化模型(RRT-1模型和RRT-2模型),在开行2种速度的客运专线上加以验证,分别研究鲁棒算法和鲁棒性代价,但其求解存在样本规模大、概率分布不明、NP-hard等不足之处。
Max-plus代数法可以在特定规则下实现矩阵运算,建立并求解具有一定运算规模的离散线性系统模型,目前已成功应用于系统制造、交通运输系统等领域。交通运输系统是典型的离散事件动态系统,目前Max-plus代数法已成功应用于铁路系统,将铁路运行的过程类比为串行生产线上工件依次顺序加工的过程。文献[3]基于Max-plus代数法的极大时间约束,研究轨道交通系统开环和闭环周期的运行规律。文献[4-5]通过极大代数框架评价了轨道交通系统及运行图的稳定性。由于快慢车模式中的快车在列车事件时序上会发生跃迁,现有的Max-plus列车运行系统闭环模型无法模拟快车越行、通过事件。基于此,本文提出一种基于Max-plus代数法的市域铁路快慢车运行系统的闭环模型,用状态变量的解生成满足运行方案需求的列车时刻表,并分析运行系统的稳态特性。本文研究可为市域铁路快慢车运行的计划编制和鲁棒性检验提供理论依据。
1 Max-plus离散事件动态系统与列车运行过程
假设市域铁路上有S1,S2,…,Sq共q个车站,假设已确定列车开行方案,计划每周期从S1到Sq站开行m列列车,表示为P1,P2,…,Pm。任一列车Pi(i=1,2,…,m)在每个非首末站均包含到达和出发两个事件,始发站仅有出发事件,终点站仅有到达事件。为了表述列车在车站的到发作业时刻,将列车在每一站Sj(j=1,2,…,q)发生的事件一一对应,共建立2q-2个车站作业点,为标注方便,重新编号车站作业点为W1,W2,…,Wn,其中n=2q-2。车站、列车事件与车站作业点之间的映射关系如图1所示。

图1 车站、列车事件与车站作业点之间的映射关系
1.1 定义模型变量和参数
假设只存在S1—Sq站单一交路,车底充足,不考虑车底衔接。线路运行方案已知,即列车在区间和站点的作业时间、列车追踪间隔等均为已知参数,利用Max-plus代数法描述满足运行方案条件下的列车运行全过程,记录每一列列车运行状态迁移,求解列车到发事件发生时刻。
1) 状态变量xij。记录列车Pi运行状态跃迁至车站作业点Wj的时刻,即列车Pi在始发车站S1的发车时刻(作业点位置为W1)记为xi1;以此类推,在第p个车站Sp的到达时刻(作业点位置为Wj)记为xij,出发时刻(作业点位置为Wj+1)记为xi,j+1,在终点站Sq的到达时刻(作业点位置为Wn)记为xin。
2) 输入变量ui。记录每列列车计划在始发站S1的发车时刻。
3) 输出变量yi。记录每列列车在终点站Sq完成停站作业的时刻。
4) 作业时间tij。列车Pi的运行状态从一站作业点跃迁至另一站作业点所需时间。例如:列车Pi在车站作业点W1的作业时间,表示列车Pi从S1站出发至S2站的区间运行时间,记为ti1;列车Pi在车站作业点W2的作业时间,表示列车Pi从到达S2站至由S2站出发所需时间,即列车Pi在S2站的停站作业时长,记为ti2。在实际问题求解中,区间运行时间不为0,停站作业时长可为0(表示列车在该站越行,不停车通过)。
5) 追踪间隔时间zij。列车Pi在车站作业点Wj与下一列车Pi+1之间的追踪间隔时间。
6) 周期T和批次k。设定若干列车为一个列车群,在一个批次内从始发站间隔发车,此后列车运行计划按批次重复循环,列车开行复现时间间隔称为一个周期T。k表示第k批次。模型参数周期与批次示意图如图2所示。
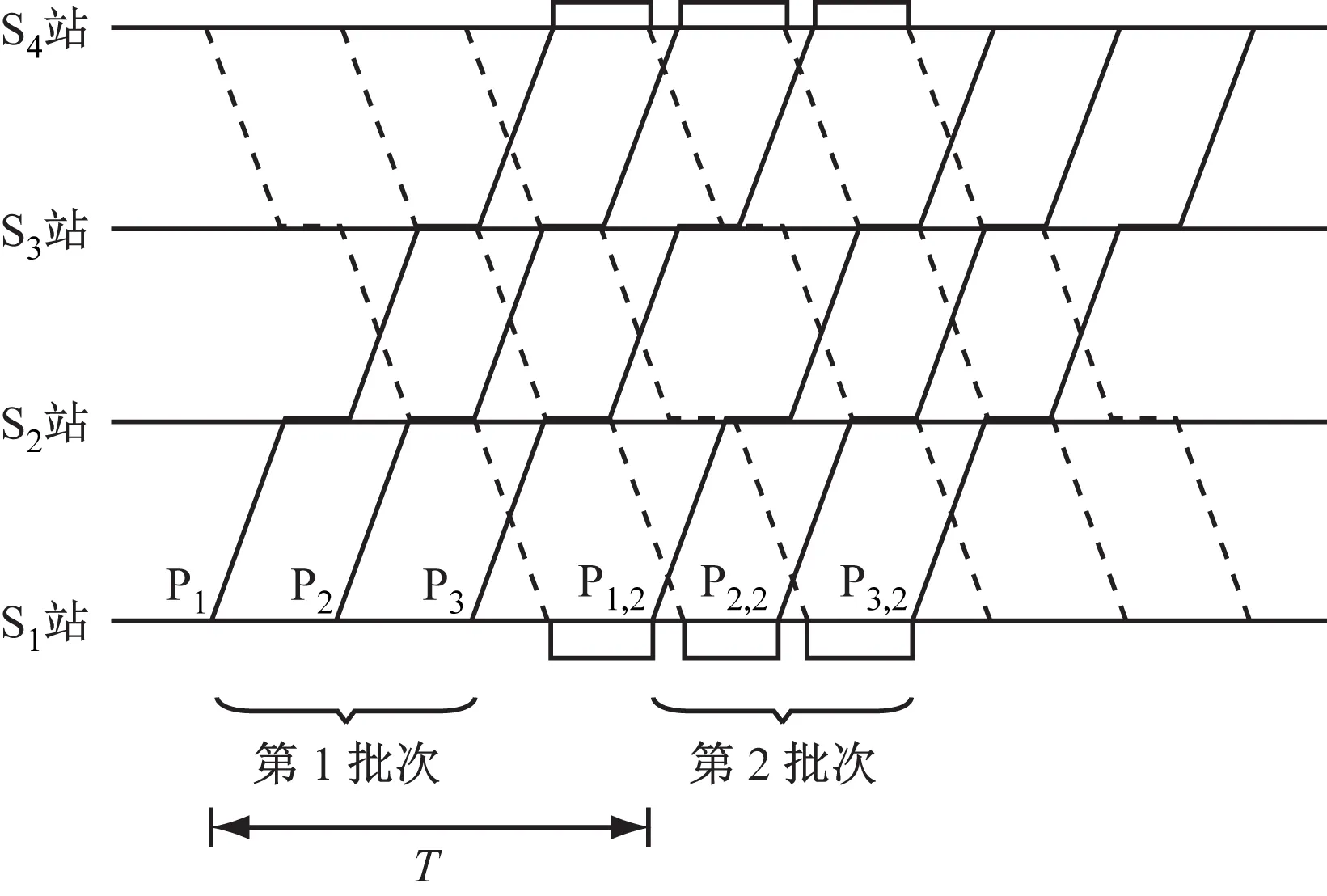
图2 模型参数周期与批次示意图
1.2 系统约束规则
1) 首班车P1状态。始发站出发时刻受初始既定时刻的约束;在非始发站首班车的到发时刻受自身接续规则的约束。Max-plus代数形式可以分别表示为:
x11(k)=max{u1}=0⊗u1(k)
(1)
x1j(k)=x1,j-1(k)⊗t1,j-1
(2)
j=2,3,…,n
式中:
x11(k)、x1,j-1(k)、x1j(k)——在第k批次中,首班车P1运行状态分别跃迁至车站作业点W1、Wj-1、Wj的时刻;
u1(k)——在第k批次中,首班车P1计划在始发站S1的发车时刻,数值上等于x11(k);
t1,j-1——首班车P1从作业点Wj-1跃迁至作业点Wj所需时间。
2) 非首班列车Pi(i≠1)状态。始发站出发时刻受初始既定时刻和列车追踪间隔时间的约束;非始发站首班车到发时刻受自身接续规则和列车追踪间隔时间的约束。Max-plus代数形式可以分别表示为:
(3)
i≠1
xij(k)=xi-1,j(k)⊗zi-1,j⊕xi,(j-1)(k)⊗ti,(j-1)
(4)
i≠1,j=2,3,…,n
式中:
xi1(k)、xi,j-1(k)、xij(k)——在第k批次中,列车Pi运行状态分别跃迁至车站作业点W1、Wj-1、Wj的时刻;
xi-1,1(k)、xi-1,j(k)——在第k批次中,列车Pi的前列列车Pi-1运行状态跃迁至车站作业点W1、Wj的时刻;
ui(k)——在第k批次中,列车Pi计划在始发站S1的发车时刻;
ti,j-1——列车Pi从作业点Wj-1跃迁至作业点Wj所需时间;
zi-1,1、zi-1,j——列车Pi的前列车Pi-1分别在车站作业点W1、Wj时与列车Pi之间的追踪间隔时间。
3) 输出条件yi。y1—ym表征在一个周期内,第i(i=1,2,…,m)列列车在终点站完成停站作业的时刻,可以表示为:
yi(k)=xin(k)⊗tin
(5)
i=1,2,…,m
式中:
yi(k)——在第k批次中,列车Pi在终点站完成停站作业的时刻;
xin(k)——在第k批次中,列车Pi运行状态分别跃迁至终点站作业点Wn的时刻;
tin——列车Pi在终点站作业点Wn的停站作业时间。
2 基于Max-plus代数法的列车时刻表编制模型
2.1 列车运行系统Max-plus开环线性模型
首先,基于Max-plus代数法建立站站停运行模型。列车P1,P2,…,Pm按间隔时间依次发车,每列列车依次通过每个车站,并依次到达终点站完成一个周期的运行过程,期间前后接续列车次序保持固有顺序。站站停列车运行计时事件图如图3所示。
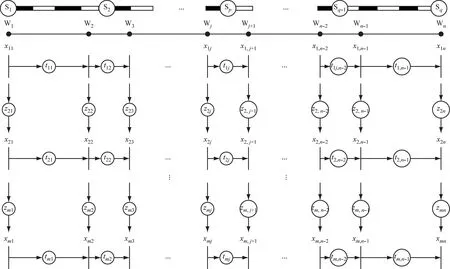
图3 站站停列车运行计时事件图
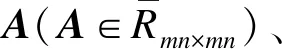
x(k)=Ax(k)⊕Bu(k)
(6)
y(k)=Cx(k)
(7)
(8)
(9)
(10)
(11)
(12)
式中:
Ji——自身接续约束矩阵(未标注的元均为ε元),非零元记录第i(i=1,2,…,m)列列车依次在第1,2,…,n-1个车站作业点的作业时长;
Ii——列车追踪间隔约束矩阵(未标注的元均为ε元),非零元记录第i(i=1,2,…,m)列列车依次在第1,2,…,n-1个车站追踪列车的发车间隔时间zi1,zi3,…,zi,n-1,以及追踪列车的到达间隔时间zi2,zi4,…,zin。
由于同一区间列车的运行时间相同,且同一车站的停站时长相同,则有J1=J2=…=Jm,I1=I2=…=Im。B中无标注的元均为ε元,矩阵B中的单位元素分布在第1行和第n的整数倍+1行。C中无标注的元均为ε元,矩阵C中的非零元分布在第n的整数倍列。
对于式(6),在表达式两端逐次左圈乘矩阵E,A,A2,…,Ap-2,Ap-1,再将各方程迭代相加可推导出:
x(k)=A*Bu(k)
(13)
A*=E⊕A⊕A2⊕A3⊕…⊕Ap-1
(14)
代入式(7),输出解表达式为:
y(k)=CA*Bu(k)
(15)
2.2 快慢车模式下开环线性模型的变换
快慢车模式下,由于存在快车越行慢车,运行图编制的特点在于考虑列车停站分布和运行顺序变换,在列车运行系统线性模型中,这两者对应于系统状态矩阵参数的重新赋值与排序。假设开行1列快车P3,且设定在S2站越行。列车P3在车站S2越行前后的方案示意图如图4所示。
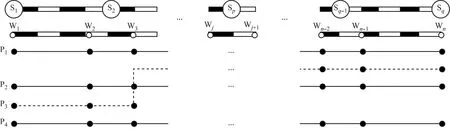
图4 列车P3在车站S2越行前后的方案示意图
快车P3在S2站办理通过作业,即停站时长为0,在系统状态矩阵中表示为t32=0 在列车运行开环线性模型中(见图4),越行不会改变列车自身的接续约束,即自身接续约束矩阵Ji无变化。越行会对快车P3、越行前列列车P2和越行后的列车P4这3列列车在越行后的次序有所影响,即3列列车在车站作业点W3,W4,…,Wn的状态方程都将发生改变。 以3列列车在车站作业点W3的状态方程变换为例: (16) (17) (18) (19) 除了A的矩阵元素位置转移外,z13、z23的取值也发生了变动。站站停模式下,z13、z23均表示S2站追踪列车发车间隔时间,即z13=z23;快慢车模式下,z13、z23表示S2站列车同向通发(通过和发车)、发通(发车和通过)追踪间隔时间。B、C与其他变量矩阵均不做状态置换。 编制规律性的列车运行计划有利于提高乘客的出行选择黏性。为使系统形成周期性运行节奏,建立列车运行系统闭环模型。引入反馈方程,即U(k)=K⊗Y(k-1),K为m×m的常数矩阵,其元素ki,j满足以下关系式: (20) i,j=1,2,…,m 式中: Ki——反馈常数,表示批次间的列车发车间隔约束。 列车运行系统的闭环线性模型为: y(k)=My(k-1),k=2,3,…,N+ (21) x(k)=Nx(k-1),k=2,3,…,N+ (22) M=CA*BK (23) N=A*BKC (24) 假设某市域铁路上的4个车站S1—S4,其中车站S2具备越行条件。已知运行方案为:计划每20 min(列车计划运行周期T=1 200 s)周期在上行方向(S1→S4)开行同一批次的4列列车P1—P4,慢车和快车以1∶1间隔开行,快车在S2站越行。案例区段各车站及区间时间参数如表1所示。 表1 案例区段各车站及区间时间参数 利用Max-plus代数法建立快慢车运行上行方向闭环模型。 输入系统的初始取值为:u=[u1u2u3u4]T=[0 140 600 740]T,表示每列车在S1站的发车时刻。 服务时间矩阵F取值为: 反馈矩阵K中的反馈元素Ki取0,构建闭环模型。闭环系统输出矩阵M为: 累计计算6个周期(合计2 h),列车在S4终点站完成停站作业的输出时刻y(k)如表2所示。 表2 列车在S4终点站完成停站作业的输出时刻 该快慢车运行系统特征值λ为慢车运行一周期所花费的时间,即λ=909 s。系统列车计划运行周期T为1 200 s,因此一个周期系统的缓冲时间为: Δ=T-λ=291 s 缓冲时间大于0,表示系统稳定。此外,还可通过x(k)得到对应的列车时刻表。假设首班车7:00从S1站发车,前3个批次列车在各站的到发时刻信息如表3所示。 表3 前3个批次列车在各站的到发时刻信息 则系统稳态参量(特征值)λ对于元mij的增性摄动是鲁棒的。通过常用的准则来定量刻画稳态参量λ相对于系统矩阵各元素mij的鲁棒性,定义鲁棒性准则RF(mij)和RM(mij)分别为[4]: (25) (26) 考察鲁棒性准则RF(mij)和RM(mij)(符号“-”表示该位置不属于摄动元),则有: (27) (28) 考察鲁棒性准则RM(mij),若RM(mij)=0,则λ对于RM(mij)是非鲁棒的。前文案例中,RM(m11)=RM(m33)=0,即首班车在始发站出发时刻不具备鲁棒性,第4列列车为快车,越行后成为第3列列车,在越行站越行时刻不具备鲁棒性;若RM(mij)≠0,则λ对于RM(mij)是鲁棒的,且RM(mij)的值越大,鲁棒性程度越高。 编制快慢车运行计划时,应满足系统稳定性和 鲁棒性的要求。为考察快慢车方案的系统稳态特征,本文针对市域铁路快慢车运行特点,基于Max-plus代数法构建市域铁路快慢车运行系统闭环模型。以一段计划开行快慢车的市域铁路为例,从变量输入到系统输出演化求解了列车运行动态转移的全过程,并通过状态转移变量矩阵的求解结果生成列车运行时刻表,分析该系统的稳定性和鲁棒性,实现了Max-plus代数法在市域铁路快慢车运行系统上的应用,为快慢车运行计划编制和系统鲁棒性分析提供了一种新的分析模型。目前,所提Max-plus代数法模型仅限于在满足已知运行方案要素条件下生成快慢车运行时刻表和系统稳态特性评价,下一步还可深入分析Max-plus代数法在快慢车系统鲁棒性优化和列车运行调整方面的研究。
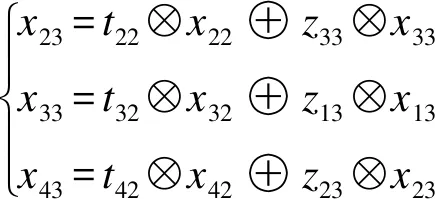
2.3 列车运行系统Max-plus闭环线性模型
3 算例分析
3.1 市域铁路快慢车闭环模型输出演化



3.2 单参数摄动情形的鲁棒性分析
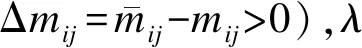

4 结语

