蜗轮齿面刀痕打磨接触力获取方法研究

常旭,赵康,陈家荣

（上海工程技术大学机械与汽车工程学院,上海 松江 201600）

目前,包络环面杆副中的蜗轮主要通过滚齿机进行加工,加工之后的蜗轮齿面不可避免地会产生刀痕,需要进一步在不同负载（25%、50%、75%、满负载）下进行多次跑合[1-3],以消除蜗轮齿面刀痕并达到齿面啮合精度,这种去除蜗轮齿面刀痕的方法工艺复杂,效率很低.为提高蜗轮加工效率,在蜗轮经过滚切之后,使用工业机器人打磨蜗轮齿面刀痕,完成对蜗轮齿面的粗加工,并在满负载状态下进行一次跑合即可完成蜗轮精加工.工业机器人打磨加工虽然具有效率高、成本低、一致性高等优点,但是尚需精确获取工业机器人末端与蜗轮齿面之间的接触力以实现柔顺控制.

在接触力精确获取的研究上,文献[4-5]建立的重力补偿计算模型只考虑了机器人末端工具重力,没有考虑机器人安装倾角、传感器零点和噪声影响,而且仅进行了仿真分析,没有实验验证；文献[6-7]提出了一种基于力传感器重力补偿的机器人柔顺控制方法,建立了重力补偿数学模型,通过采集不同位姿下力传感器数据,计算机器人底座安装倾角、力传感器零点数据、末端工具重力及重心坐标,但是没有考虑力传感器采集的数据含有噪声的影响；文献[8-9]针对六维力传感器的重力补偿提出了一套完整的标定与计算方法,综合考虑了机器人安装倾角、传感器零点、工具重力和重心以及噪声的影响,但是计算过程较为复杂；文献[9]根据力等效原理,建立了零点校正和重力补偿数学模型,通过至少3 个机器人的不同位姿计算出传感器零点、安装倾角以及重力补偿参数,但是缺少力跟踪控制实验,没有验证实际应用中力跟踪效果.

本文主要对工业机器人与蜗轮齿面交互过程中真实力感知信息的获取方法进行了研究, 为实现工业机器人柔顺打磨蜗轮齿面刀痕奠定基础.

1 接触模型构建

在工业机器人打磨蜗轮齿面刀痕过程中,末端安装的电主轴始终与蜗轮齿面平行,末端与工件的坐标系如图1 所示,工业机器人传感器坐标系{Ts}姿态在打磨加工时始终与打磨台坐标系{Tb2}保持一致.工业机器人打磨蜗轮齿面刀痕过程较为复杂,直接对打磨进行理论分析难度系数较大,并且加工倾角、打磨深度、进给速度等外在因素的细微变化都会影响打磨过程中打磨力的变化.在工业机器人打磨加工过程中,为保护蜗轮齿面不被过切,在设置轨迹时要留有余量,设置的末端轴向打磨量远大于径向打磨量,在这种情况下需要考虑蜗轮齿面受到的径向力,即法向力.假设在打磨时所产生的力平行于高速电机主轴,那么在理论分析时就可以将打磨过程转变为打磨曲面的打磨过程,在打磨时需要控制垂直于打磨轨迹的法向力,即X 轴方向的力.

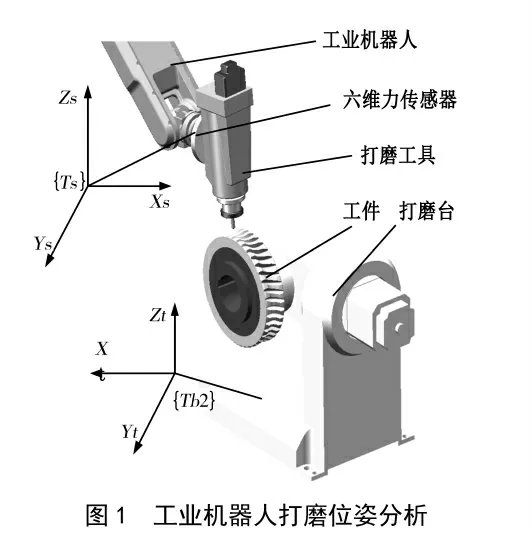
图1 工业机器人打磨位姿分析Fig.1 Analysis of grinding pose of industrial robot

在蜗轮齿面刀痕打磨系统的笛卡尔操作空间中,对打磨工具坐标系{Tt}进行力/位分解,Xt方向进行恒力控制,且始终保持水平,即打磨姿态为b1Rt=[1 0 0]T,Yt、Zt方向进行位置控制.由运动学模型计算得到打磨工具末端的位置为

式（1）中:Tb1表示工业机器人基坐标系,Tf表示工业机器人末端坐标系,Tt表示打磨工具末端坐标系,Tb2表示打磨台中心坐标系,Ts表示六维力传感器坐标系,Tj表示工件坐标系.

2 工业机器人末端与蜗轮齿面交互力预处理

2.1 力噪声预处理

卡尔曼滤波器[10]是一种由线性系统状态方程通过迭代更新最优估计系统最佳状态的滤波器,即使有诸多不确定信息,卡尔曼滤波器也能找到不易察觉的相关性.卡尔曼滤波器在对力感知信息进行估算的过程中,只需要考虑系统的过程噪声、测量噪声以及系统当前状态,不需要对整个过程的数据进行采集、保存,占用内存少,因此非常适用于力感知信息实时在线处理[11].

将卡尔曼滤波器的状态变量设计为六维,分别是六维力传感器采集的三维力信息:Fx、Fy、Fz与三维力变化信息：,观测变量为三维力信息:Fx、Fy、Fz.六维力传感器采集力感知信息的迭代方程可简化为如下二阶方程

式（2）可化简为

系统的状态方程为

式（3）中:Xt表示工业机器人打磨系统t 时刻状态变量,A 表示工业机器人打磨系统状态转移矩阵,T表示采样周期,Ut表示工业机器人打磨系统过程噪声.

工业机器人打磨系统的观测方程可表示为

式（4）中:Zt+1 表示工业机器人打磨系统t+1 时刻的观测变量,H 表示工业机器人打磨系统观测矩阵,Vt表示工业机器人打磨系统的测量噪声.卡尔曼滤波器以迭代的方式对系统进行最优在线估计,更新的过程包括时间更新和状态更新,其中状态更新包括模型预测和观测两个过程,迭代方程由式（5）表示.

2.2 重力补偿

2.2.1 工业机器人安装倾角和末端工具重力计算一般情况下,工业机器人在安装时很难保证工业机器人处于水平平面,会与水平面存在一定的倾斜角度,因此在实际中工业机器人的基座标系与实际坐标系并不重合.如图2 所示,建立工业机器人的坐标系,定义Tw-X0Y0Z0为世界坐标系,Z0轴竖直向上,T1-X1Y1Z1为机器人基座标系,Ts-XsYsZs为六维力传感器坐标系,工业机器人基座标系由世界坐标系先绕X0轴旋转u,再绕Y0轴旋转v 得到.六维力传感器实际测量数据记为：F=[f x,f y,fz]、M=[mx,my,mz],六维力传感器的零点数据记为,打磨工具在力六维传感上的作用力与力矩记为：G=[g,g,g]、M=[m,m,m].

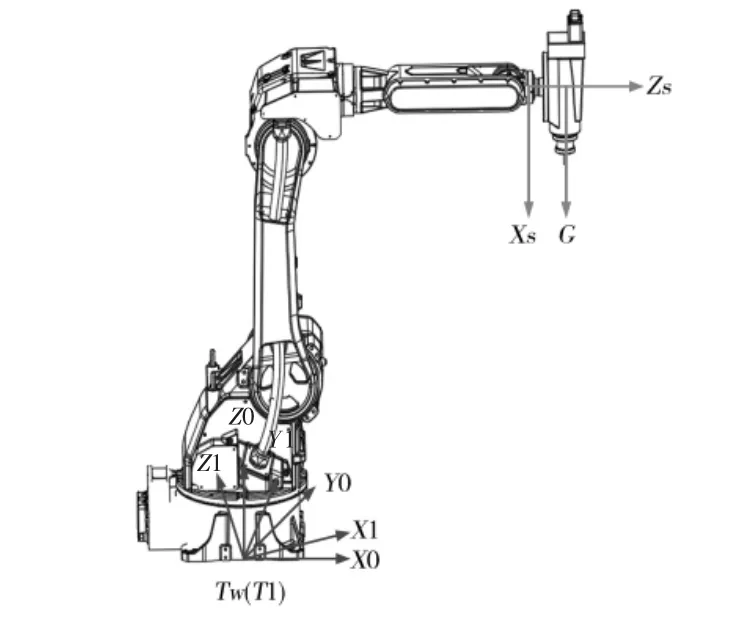
工业机器人未与环境发生交互作业时,六维力传感器实际上测量的数据是打磨工具在六维力传感器上产生的力与力矩和六维力传感器零点之和,所以

式（6）中：u、v 表示工业机器人的安装倾角.

令

式（7）中：l 是3×3 单位矩阵.

测量N（N≥3）组工业机器人不同姿态下六维力传感器数据,代入式（7）得到

进一步可化简成

通过矩阵变换得到

由式（8）可计算出六维力传感器的零点分力以及常数l、l、l.

同时可计算出工业机器人底座的倾斜角以及末端打磨工具重力为

2.2.2 六维力传感器零点与末端工具中心坐标计算末端打磨工具重心在六维力传感器坐标系Ts中的位置记为,在六维力传感器上产生的力和力矩如图3 所示,可求得打磨工具重力在六维力传感器上的力矩计算公式

式中：P为块段中锆英石、或钛铁矿矿物量，t；V为块段体积，m3)；C为块段锆英石或钛铁矿的平均品位，kg·m3。

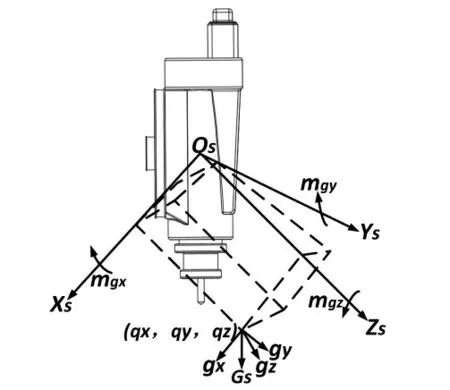
图3 末端工具作用在六维力传感器上的力矩示意图Fig.3 Torque diagram of the end tool acting on the six-dimensional force sensor

联立式（6）与式（9）可得

令

故式（10）可整理成

同样选取N（N≥3）个工业机器人末端打磨工具不同姿态下的六维力传感器数据,代入式（11）可以求得工业机器人末端打磨工具重力在六维力传感器上的坐标p、p、p以及b、b、b.

由联合式（10）和式（11）可求得

综上公式计算,可以计算出六维力传感器零点值：,工业机器人末端打磨工具重力G 和重心坐标q=[q,q,q].

2.2.3 重力补偿值以及负载重力计算由式（8）（11）可以求出打磨工具重力在六维力传感器坐标系上的力和力矩分量.故需要在六维力传感器坐标系上补偿的力和力矩为

对六维力传感器进行重力补偿之后,打磨工具末端接触的真实力和力矩为

3 基于位置的阻抗控制

基于位置的阻抗控制[12]是一种适用于解决工业机器人与环境交互问题的控制策略,它建立了工业机器人与环境之间接触力误差和工业机器人运动变量之间的函数关系,实现了工业机器人末端力控制.因为其不需要精确的动力学模型,所以被广泛地应用于工业机器人控制领域[13,14].基于位置的阻抗控制架构如图4 所示,主要由位置控制内环和力控制外环组成,其中Xd表示期望位置,Xe表示实际位置,Fe表示六维力传感器采集的实际接触力,即工业机器人与环境的接触力,Fe'表示预处理后的实际接触力,ΔF表示力误差,Fd表示期望接触力,ΔX 表示期望位置与实际位置的偏差,即对位置的阻抗补偿量,力误差ΔF 与位置补偿量ΔX 的阻抗关系可用式（13）表示.

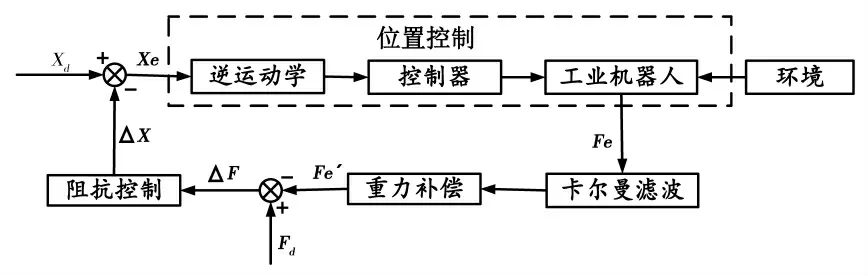
图4 基于位置的阻抗控制架构图Fig.4 Architecture diagram of impedance control based on position

式（12）中:M 表示质量参数矩阵,B 表示阻抗参数矩阵,K 表示刚度参数矩阵.

由于位置的阻抗控制中力控制和位置控制相互耦合以及六维力传感器采集的力感知信息以一定的频率传送给连续的阻抗控制,因此为了使力控制与位置控制尽可能地分离,需要对连续的阻抗控制进行时域离散化[15-17].另外,为了便于对工业机器人末端三个方向进行柔顺力控制以及方便调节阻抗参数,本文简化阻抗控制模型,即认为机器人末端在X/Y/Z 三个方向的运动相互解耦[18-19].以其中的X 方向为例,由图3 可得

式（13）中：e 表示期望位置与实际位置之差,ke表示环境刚度,表示机器人末端与环境的接触力,xc表示未发生变形前的位置,xe表示环境当前实际位置.

由式（13）可得：

将式（13）（14）进行La-place 变换并化简可得

所以系统稳态力跟踪误差为

显然要使力跟踪稳态误差为零,满足式（15）中任一条件即可,但在实际的工业机器人交互作业过程中,由于工业机器人末端刚度跟随环境实时变化,因此实时、准确地获取刚度值很困难.为了简化处理,本文将刚度参数kd设置为零,因此式（13）的阻抗控制函数可以化简成

令x=v=,其中v 代表速度,则式（13）可化简为

对式（16）求解可得

将式（17）离散化,假设系统采样周期为Δt,在采样周期内惯性参数md、阻尼参数bd为常数,令,可以得到工业机器人末端接触力与机器人控制速度的表达式为

故位置补偿量ΔX 的表达式为

4 实验验证与仿真分析

4.1 卡尔曼滤波器在线滤波实验

根据实验现场实际情况,卡尔曼增益初始值=1,为了保证卡尔曼滤波器收敛,先验估计协方差设定为:.将系统过程噪声和系统采集观测噪声分别设定为

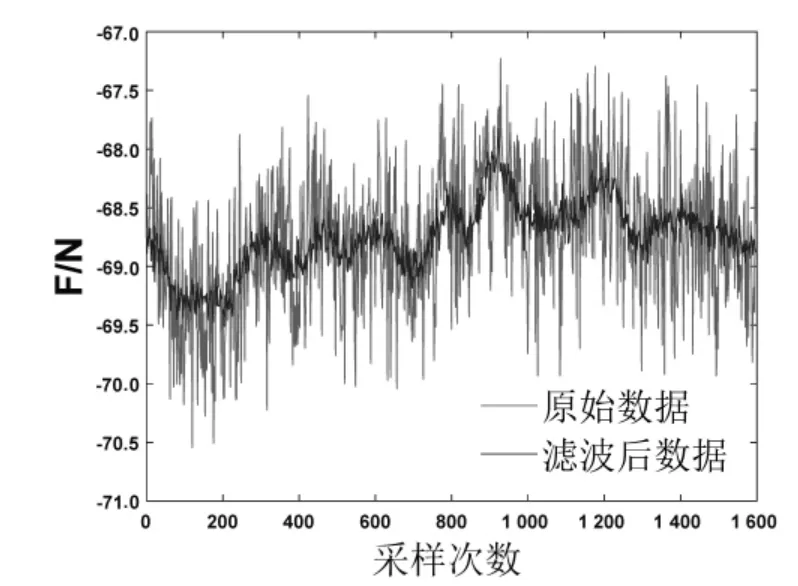
实验时,六维力传感器实时采集打磨过程中的力感知信息,然后使用卡尔曼滤波器实时处理采集得到力感知信息.本文以X 方向的力信息滤波处理结果为例说明卡尔曼滤波器的处理效果.图5、6 表示对平稳力感知信息的处理效果,在未处理前力信息在±3 N 之间波动,卡尔曼滤波器处理后,波动值降到±1 N之间,使采集得到的力信息更加平稳,降低了外界因素对六维力传感器采集力感知信息的干扰.图3-7表示非平稳力感知信息的处理效果,结果表明卡尔曼滤波器能够适应采样值的变化,达到减少外界影响的目的.

4.2 重力补偿实验

为验证本文重力补偿算法的效果,根据传感器标定及重力补偿算法进行工业机器人在线重力补偿与传感器零点标定实验.首先测量工业机器人安装倾角、末端工具重力、六维力传感器零点以及末端工具中心.将工业机器人末端的位姿设置为如图7 所示的6 种姿态.为了减少未知因素带来的误差,每种姿态连续采集600 组数据求平均值, 并且每组数据采集时均经过卡尔曼滤波器滤波,6 种姿态下六维力传感器的力感知信息测量值如表1 所示.

图7 机器人姿态示意Fig.7 Robot posture diagram

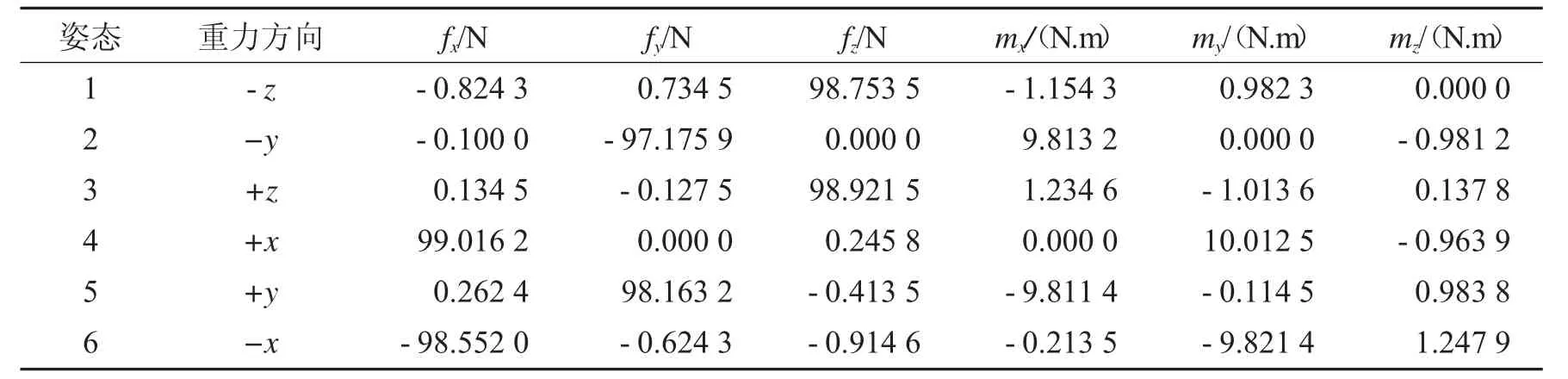
my/（N.m）0.982 3 0.000 0-1.013 6 10.012 5-0.114 5-9.821 4姿态123456重力方向-z-y+z+x+y-x fx/N-0.824 3-0.100 0 0.134 5 99.016 2 0.262 4-98.552 0 fy/N 0.734 5-97.175 9-0.127 5 0.000 0 98.163 2-0.624 3 fz/N 98.753 5 0.000 0 98.921 5 0.245 8-0.413 5-0.914 6 mx/（N.m）-1.154 3 9.813 2 1.234 6 0.000 0-9.811 4-0.213 5 mz/（N.m）0.000 0-0.981 2 0.137 8-0.963 9 0.983 8 1.247 9

根据表中数据以及本文所提及的重力补偿算法,可以计算得出六维力传感器的零点、安装倾角、工具重力和打磨工具在传感器坐标系下质心的位置

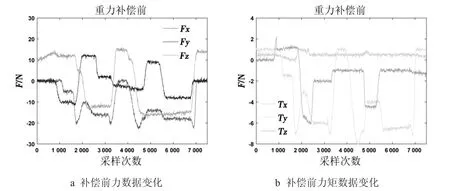
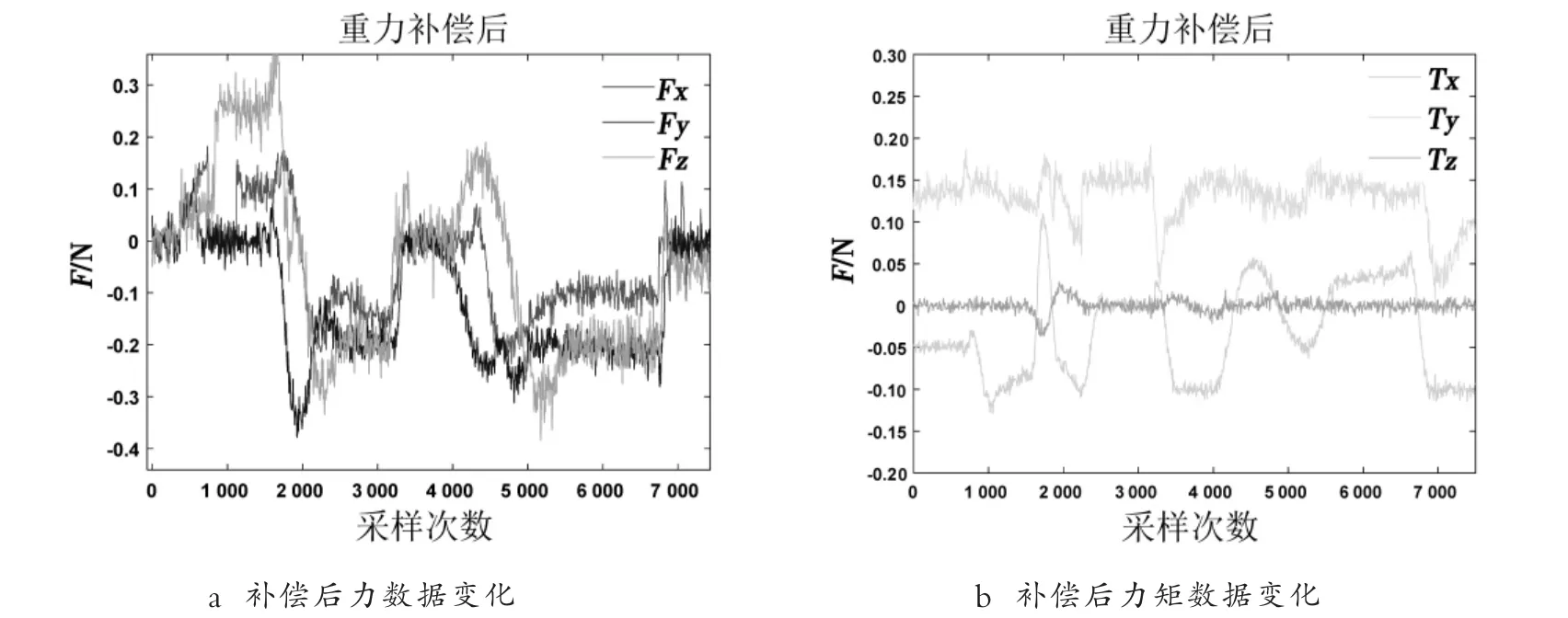
在工业机器人打磨蜗轮齿面刀痕的过程中,末端位姿会随着打磨轨迹不断变化,末端负载在六维力传感器中的分量也会随着末端位姿不断改变,所以在标定力传感器零点和工具重力之后,也要验证标定算法和重力补偿算法在工业机器人运动过程中的补偿效果.具体实验方法是:使用示教器控制工业机器人夹持打磨工具在自由空间运动任意一条轨迹,工业机器人运行速度设置为7 mm/s,采集运动过程中六维力传感器读数,且采集时力感知信息已经经过卡尔曼滤波器处理.图8 表示未经过重力补偿时六维力传感器的读数,图9 表示重力补偿后六维力传感器的读数.由图8、9 中数据可以看出六维力传感器未进行补偿时,传感器读数偏移较大且随着工业机器人位姿变化而变化,经过重力补偿后,六维力传感器数据的读数误差维持在±0.4N 之间,力矩误差维持在±0.16 N·m 之间,其读数均在零点附近波动,验证了零点标定、重力补偿算法的有效性.

4.3 机器人柔顺打磨实验

工业机器人柔顺打磨实验,是在进行滤波、重力补偿的基础上,通过六维力传感器测量打磨工具末端与蜗轮齿面的接触力,完成对蜗轮齿面刀痕的柔顺打磨,如图10 所示.实验中设定恒定打磨力为20N,控制蜗轮齿面表面法向力为恒力,分别对两个齿面进行打磨,其中一个齿面利用没有进行力感知信息预处理的工业机器人系统进行打磨,另一个齿面使用本文搭建的工业机器人打磨系统进行打磨.打磨过程中法向受力如图11 所示.相比于传统工业机器人打磨系统,本文搭建的打磨系统,经过力感知信息预处理后,恒力打磨时力的波动更小,更加稳定,有效地减少了环境、误差带来的影响.

为进一步验证本文力感知信息处理方法的效果,手持粗糙度测量仪对两个齿面的表面粗糙度进行测量,分别对不同区域进行五次测量,且两个齿面测量的区域相同,测量结果如表2 所示.可知在传统打磨系统,即无力感知信息预处理时,蜗轮齿面粗糙度为0.902 μm,而本文搭建的打磨系统的力感知信息预处理时,蜗轮齿面粗糙度为0.801 μm,打磨后蜗齿面轮表面质量明显改善.

处理方式无处理有处理测量一0.912 0.792测量二0.894 0.784测量三0.904 0.807测量四0.914 0.821测量五0.887 0.801均值0.902 0.801

5 小结

本文提出了一种蜗轮齿面刀痕打磨工业机器人接触力获取方法.针对工业机器人打磨过程中环境温度、机器人振动等噪声造成力感知信息波动的问题,建立了卡尔曼滤波数学模型；考虑到工业机器人底座安装倾角、工具重力和六维力传感器零点的影响,建立了六维力传感器的零点校正和重力补偿计算模型,完成了六维力传感器的卡尔曼滤波和重力补偿实验并进行了数据分析.实验结果显示,六维力传感器数据的读数误差维持在±0.4 N 之间,力矩误差维持在±0.16 N·m 之间,其读数均在零点附近波动.与传统的工业机器人打磨系统相比,经过力感知信息预处理的工业机器人打磨系统更加稳定、精确,并且加工出的齿面表面质量明显提高,为后续对工业机器人柔顺打磨蜗轮齿面刀痕的研究奠定了基础.