金沙江下游梯级水库防洪库容优化配置公式推导与应用

谢雨祚，郭生练，钟斯睿，刘 攀，王 俊，李 帅，胡 挺

(1. 武汉大学水资源工程与调度全国重点实验室，湖北 武汉 430072；2. 中国长江三峡集团有限公司流域枢纽运行管理中心，湖北 宜昌 443133)

《长江流域综合规划(2012—2030年)》[1]明确了长江干支流水库相应的防洪任务。金沙江下游乌东德-白鹤滩-溪洛渡-向家坝梯级水库陆续建成与投入运行，在满足川渝河段防洪安全的同时，可配合三峡水库有效分担长江中下游流域的防洪压力，在长江流域防洪体系中占有极其重要的位置[1]。然而，这4个大型水利枢纽工程分别由不同的设计单位、在不同的时间依据《水利水电工程设计洪水计算规范：SL44—2006》[2]采用单站的资料系列推求设计洪水，根据四库规划设计的防洪能力适当分配以确定各个水库的防洪库容[1]，没有考虑梯级水库之间防洪库容的互补关系和上游水库调蓄对下游的影响。

周新春等[3]和谢雨祚等[4]均认为，对具有共同防洪任务的水库群，梯级水库间防洪库容的互补关系受洪水地区组成的空间分布及洪水发生规律影响。若梯级水库属同一流域且区间的流域面积较小，下库回水几乎与上库坝下相连，则梯级水库的防洪库容具有近似等效作用[5-6]。康玲等[7]提出了水库群联合防洪调度系统非线性安全度策略，构建了水库群防洪库容优化分配模型，以长江上游梯级水库群为实例探讨了水库群系统非线性安全度策略的防洪效果。何志鹏等[8]基于6场典型年的洪水过程，建立了变权重剩余防洪库容最大、系统非线性安全度最大和梯级防洪风险率最小3种防洪库容优化分配模型，应用于金沙江下游梯级水库并采用逐次淘汰法对各个模型的计算结果进行综合评价。顿晓晗等[9]基于长系列历史实测径流资料，推算了防洪库容频率曲线方法，研究了溪洛渡、向家坝水库与三峡的防洪库容分配及互用性问题。然而，现有的防洪库容优化配置研究往往聚焦于梯级水库的防洪调度及风险分析，对梯级水库的发电效益研究较少。为顺应新时代水利高质量发展需求，在不改变同河段上梯级水库总预留防洪库容且不降低原设计阶段防洪标准的前提下，如何优化配置这些水库的防洪库容以提高梯级水库的发电效益，具有重要的理论研究价值和实际意义。

本文基于防洪库容总量不变原则，采用数学公式推导法开展金沙江下游乌东德-白鹤滩-溪洛渡-向家坝梯级水库(以下简称金下梯级)防洪库容优化配置研究，以挖掘水资源高效利用的潜力，为水库调度决策提供科学依据。

1 金沙下游梯级水库水力联系特点与调度要求

四川省攀枝花市雅砻江口至宜宾市岷江口为金沙江下游河段，建有乌东德-白鹤滩-溪洛渡-向家坝4座水库(图1)，预留的总防洪库容约155亿m3。根据《长江流域综合规划(2012—2030年)》的总体要求与长江中下游总体防洪标准，确定金沙江河段所预留的防洪库容之后[1]，再基于对保障川渝河段和宜宾、泸州、重庆等城市的防洪安全任务[10]以及金沙江流域水库规划设计的防洪能力，将聚合防洪库容具体分配至各个水库。金下梯级坝址以上集水面积分别为40.61万、43.03万、45.44万、45.88万km2，乌东德-白鹤滩、溪洛渡-向家坝梯级水库水力联系更紧密、区间流域面积很小且没有防洪任务，白鹤滩(向家坝)水库的回水几乎到达乌东德(溪洛渡)水库的坝下，两库预留的防洪库容互补等效，可以开展防洪库容优化配置研究。

qin，1—qin，4为平均入库流量；qz，1—qz，3为区间流量图1 金沙江下游梯级水库和水文站以及川渝河段防洪任务概化Fig.1 Sketch diagram of reservoirs，hydrological stations，and flood control tasks in downstream Jingsha River

乌东德-白鹤滩、溪洛渡-向家坝梯级水库分别在7月、7—8月要配合三峡水库承担长江中下游的防洪任务。根据还原后的华弹(巧家)站和屏山(向家坝)站1940—2020年(共81 a)7—8月的天然日流量资料，采用水文比拟法计算金沙江下游梯级水库入库流量和区间流量。以梯级末位向家坝站作为控制节点，依据防洪区域分布情况及现有堤防的建设情况，金沙江段柏溪镇堤防的防洪标准为20年一遇，相应洪峰值以屏山站洪峰值代表，20年一遇洪水洪峰值为28 000 m3/s。本文控制向家坝水库出库流量不超过28 000 m3/s，以确保柏溪镇的防洪安全。根据各水库调度规程，当白鹤滩、溪洛渡、向家坝的坝上水位分别达到800、560、367 m时，乌东德、白鹤滩、溪洛渡水库尾水位—出库流量关系分别需要考虑下游水库的顶托影响。

2 研究方法

2.1 梯级水库防洪库容聚合分解

防洪库容是指防洪高水位与汛限水位之间的库容，其目的是保障水库大坝和下游防洪目标的防洪安全。由于梯级水库的防洪库容在初设阶段已经确定，需采用聚合分解理论在保证防洪库容总量不变的前提下对其进行优化配置。梯级水库防洪库容聚合的目的是确定总防洪库容大小以保证防洪安全，在维持防洪库容总量不变的基础上先聚合各水库的原设计防洪库容，梯级水库聚合防洪库容与所有子水库的优化配置后的防洪库容之和相等[11]；而对聚合防洪库容进行分解的目的是增加发电效益。在满足水库系列约束的前提下，适当地对聚合防洪库容进行分解，即优化配置，可增加梯级水库的发电效益。

梯级水库防洪库容聚合分解应满足2个条件：① 梯级水库控制面积范围内的气候特征相似且区间流域之间没有较大支流汇入；② 梯级水库共同承担对下游地区的防洪任务。前者保证了各水库的入库流量之间的相关性和同质性，后者则统一了各水库防洪库容的效用[3]。梯级水库之间的水力联系是防洪库容聚合分解的主要依据：

(1)

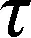
2.2 梯级水库防洪库容优化配置公式推导

梯级水库系统(水库数量≥2)防洪库容优化配置的水力发电表达式假设水库水位在涨水或退水过程中的波动影响可忽略不计，即相邻2个运行时段内m水库的库容保持不变[12]：Vm(t)=Vm，t=1，2，…，T；m=1，2，…，M。除了式(1)所示的水量平衡约束与梯级水库之间的水力联系约束外，梯级水库调度模型一般还包括水库库容约束、水库坝上水位变幅约束、水库出库流量约束和电站出力约束等[13]。数学表达式的推导可对上述约束条件进行如下简化：① 由于各个水库在汛期都会预留一定的防洪库容，根据汛期水位波动影响忽略不计假定，水库库容限制和坝上水位变幅的约束能够满足；② 为保证防洪安全，若梯级水库出库流量小于下游防洪断面安全流量，则基本满足水库出库流量约束；③ 而对电站出力限制约束，可使防洪库容优化配置后的运行水位低于电站基本达到满负荷运行状态(预想出力为装机容量)时的水位。

m水库在t时段内的多年平均发电量计算公式如下：

(2)

2.2.1两库聚合系统公式推导

(3)

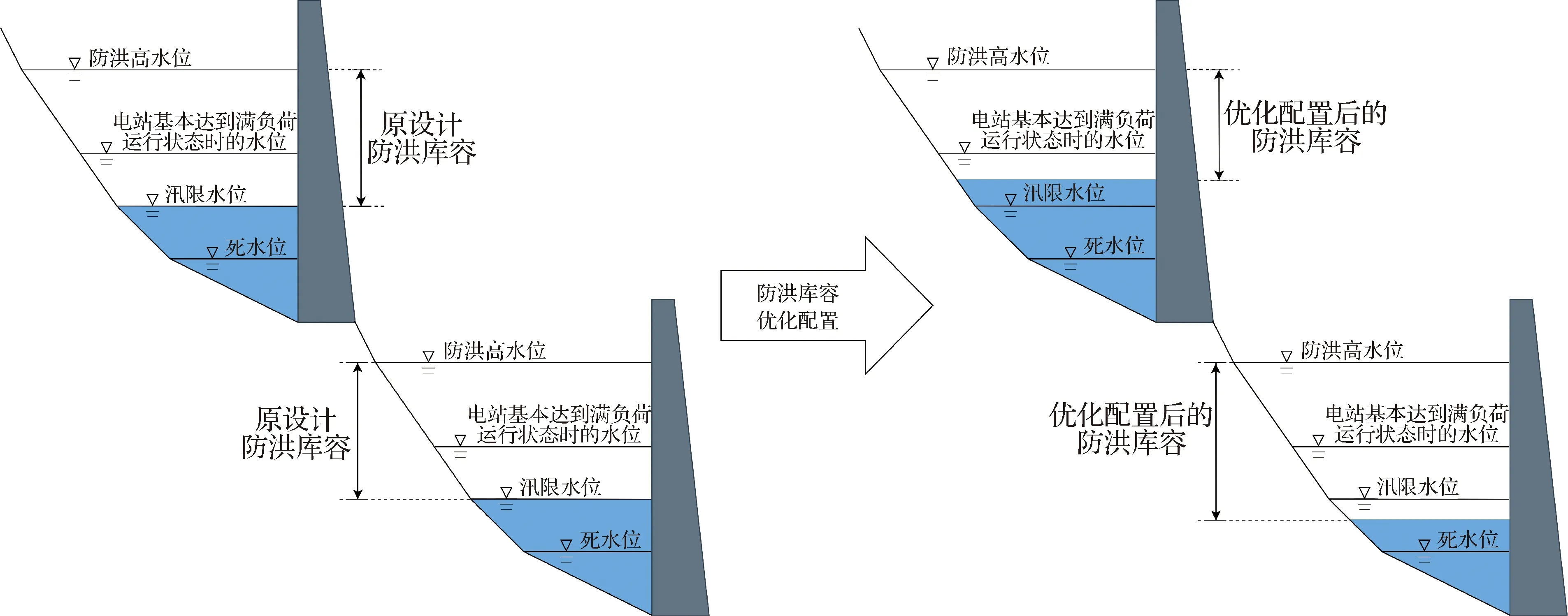
图2 两库聚合系统防洪库容优化配置示意Fig.2 Sketch diagram of optimal allocation of flood prevention storage for two-reservoir system

由于两库区间流域面积较小，防洪库容优化配置后，若下游水库运行水位抬高，上游水库的尾水位可能会受到下游水库库区回水的顶托作用，上游水库尾水位—出库流量关系函数Zd，1(g)会发生改变。由于优化配置后水库运行水位限制在电站基本达到满负荷运行状态时的水位以下，上游水库尾水位受到的顶托作用影响较小，Zd，1(·)函数变化不大。为了简化计算，公式的推导忽略下游水库的顶托作用，则两库聚合系统总发电增量为

为了更好地打造独立学院理论研究与交流的平台，突出胜利学院学报特色，积极推动全国理论界和独立学院同行们对独立学院办学思想、办学方针、办学经验和办学规律的科学研究，《中国石油大学胜利学院学报》从2008年第1期开始已设置“独立学院研究”栏目。本栏目涵盖独立学院办学思想、办学方针、办学体制、培养目标、课程建设、教学改革、师资队伍建设、招生就业制度改革等内容。热忱欢迎对独立学院有研究的相关机构、专家、学者投稿。

(4)

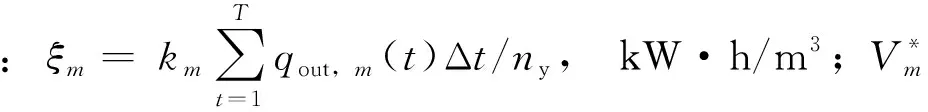
可进一步推导出：

(5)

从式(5)可以看出，∂ΔE/∂λ*的符号需要进一步计算判别：若∂ΔE/∂λ*<0，说明ΔE随λ*的增加而减小；∂ΔE/∂λ*>0时，ΔE随λ*单调递增；而∂2ΔE/∂λ*2<0说明∂ΔE/∂λ*在λ*的区间内单调减小。

2.2.2多库聚合系统公式推导与求解

由两库聚合系统防洪库容优化配置公式可推导多库聚合系统多年平均总发电增量(ΔE)：

(6)

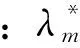
式(6)求极值问题可借用拉格朗日乘子(rλ)构造如式(7)所示的辅助函数：

(7)

式(7)可进一步推导出：

(8)

给定流量序列后，rλ是式(8)中唯一的变量，但由于各水库的地理特性差异，水位—库容幂函数关系曲线的参数bm往往不同，难以得出rλ的解析表达式。因此，采用增广拉格朗日惩罚函数法对式(8)进行数值求解，增广拉格朗日惩罚函数法通过将限制条件转化为目标函数的惩罚项，使原问题转变为无约束目标函数优化问题，且额外添加一个增广量作为惩罚[15]，可以利用有限的惩罚因子逼近最优解，且收敛速度较快。

3 金沙江下游梯级水库实例研究

乌东德、白鹤滩、溪洛渡和向家坝4座水库的防洪高水位与死水位之间的库容分别为30.20亿、104.36亿、64.62亿和9.03亿m3，将其设定为各水库防洪库容变化范围上限。需要指出的是，向家坝水库死水位370 m对应的泄流能力大于柏溪镇堤防20年一遇防洪标准28 000 m3/s，能够保证聚合系统的泄流能力。乌东德、白鹤滩、溪洛渡电站基本达到满负荷运行状态时的水位分别为964.0、803.0、571.0 m，而向家坝水库在死水位370.0 m时仍可满发，可采用文献[16]推荐的372.5 m作为限制，既可以最大限度提高发电水头，又不违背调度规程。综上所述，四库防洪库容变化范围下限分别为12.61亿、44.09亿、35.08亿和6.87亿m3，水库相关特征参数与防洪库容变化范围详见表1。

表1 梯级水库特征参数与防洪库容变化范围Table 1 Characteristic parameters and adjustable range of flood prevention storage of cascade reservoirs

以屏山站1940—2020年流量为标准，7—8月流量均大于3 000 m3/s。根据尾水位—出库流量关系函数可知，下游水库坝上水位变化量一定时(防洪库容优化配置后的水库运行水位与原设计汛限水位之差不变)，上游出库流量越大，受下游水库顶托作用的影响越小。以出库流量为3 000 m3/s计算上游水库受顶托影响的尾水位变化，当白鹤滩、溪洛渡和向家坝水库坝上水位分别位于803.0、571.0、372.5 m时，相对于汛限水位(表1)，根据各库尾水位—出库流量关系函数可计算乌东德、白鹤滩、溪洛渡水库尾水位最大变幅分别约为0.01、0.26、0.71 m，与因防洪库容优化配置导致的水位变幅相比较小(式(4))，因此下游水库顶托作用可忽略不计。

3.1 金沙江下游梯级两库聚合系统优化配置公式

采用幂函数分别拟合乌东德、白鹤滩、溪洛渡、向家坝4座水库坝上水位—库容关系曲线结果见图3，幂函数拟合公式R2均大于0.99，拟合效果好。此外，根据各水库的特征参数、7—8月天然入库流量与区间流量，汇总计算式(4)所需其他参数值如表2所示。

表2 计算式(4)的参数Table 2 Calculation parameters for equation(4)

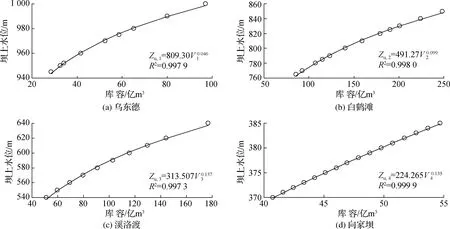
图3 金沙江下游梯级水位—库容关系幂函数拟合结果Fig.3 Relational fitting curves between reservoir water level and storage in the downstream Jingsha River

根据式(4)与表2可计算乌东德-白鹤滩和溪洛渡-向家坝聚合系统多年平均7—8月总发电增量表达式ΔE1，2和ΔE3，4如下：

(9)

(10)

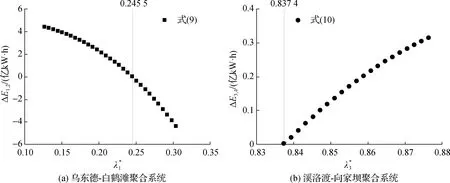
图4关系和关系Fig.4 Relational curves of

防洪库容优化配置能提高发电效益的原因分析如下：在区间来水不大的前提下，由式(2)及表2所示，水库的发电量受综合出力系数、发电流量和净水头的影响，而两库聚合系统中各个水库的综合出力系数和发电流量相近(因为入库流量相近)；由图3可知，当水库库容值发生同等量级的变化时，在汛限水位附近，库容较小的水库水位变化量大于库容较大的水库；若把库容较小水库的部分防洪库容分配至库容较大的水库后，库容较小水库的净水头增加量大于库容较大水库的净水头减少量，因此两库聚合系统的总发电量会增加。

3.2 金沙江下游梯级四库聚合系统优化配置公式

由于金沙江下游四库相距较近，两库聚合系统的防洪库容优化配置公式可以拓展至四库聚合系统，根据各个水库的防洪库容变化范围(表1)，求得乌东德、白鹤滩、溪洛渡和向家坝水库防洪库容比例系数的下限分别约为0.081、0.285、0.226和0.044。计算四库聚合系统发电增量的数学表达式ΔE1，2，3，4为

(11)

采用增广拉格朗日惩罚函数法求式(11)的极值，再探讨梯级水库防洪库容不同优化配置方案下多年平均7—8月总增发电量情况，结果汇总于表3，可以看出：① 四库考虑两两聚合时，即以乌东德-白鹤滩与溪洛渡-向家坝聚合系统为例，采用防洪库容优化配置策略相对原设计防洪库容方案可以增发电量0.97%(式(9)、式(10))；② 聚合系统中的水库数量越多，梯级水库总发电增加量越大，相对原设计防洪库容方案乌东德-白鹤滩-溪洛渡-向家坝四库聚合系统进行联合优化配置可增发电量共计10.37亿kW·h(式(11))。

表3 优化配置后的四库多年平均7—8月份发电量对比Table 3 Comparison of annual power generation of four reservoirs from July to August after optimal allocation

4 结 论

本文基于水量平衡约束及总防洪库容不变假定，以汛期发电量最大为目标，推导了梯级水库防洪库容优化配置公式并应用于金沙江下游4座水库，主要结论如下：

(1) 对两库聚合系统，适当将库容较小的水库的部分防洪库容分配至库容较大的水库，有利于增加系统的总发电效益。以乌东德-白鹤滩聚合系统为例，适当减小乌东德的防洪库容，乌东德-白鹤滩聚合系统7—8月份总发电量可增加4.45亿kW·h(1.56%)。

(2) 根据梯级水库防洪库容优化配置公式，7—8月份金沙江下游四库聚合系统可增发电量10.37亿kW·h(2.12%)，经济效益巨大。