长江石首段河岸带地下水位变化过程模拟及分析
夏军强,朱 恒,邓珊珊,周美蓉
(武汉大学水资源工程与调度全国重点实验室,湖北 武汉 430072)
河岸带是既具有水域特性、又具有陆地特性的水陆交界区域,受到河水和地下水的共同作用[1]。在河岸潜流带内,河水与地下水相互作用,使得水量和水质都进行交换,进一步影响溶质和能量的交换,最终对河岸带生物群落的生长和繁殖产生影响[2-4],是流域生态系统稳定性的重要一环[5]。因此,确定河水与地下水在河岸带内进行相互作用的范围,可以为岸线规划和管理提供依据。
河水与地下水相互作用发生在河床表面以下的沉积缓冲带或侧向河岸带的多孔渗透区内,该区域称之为潜流带[6]。早期对潜流带的研究主要是针对河床潜流带,而对河岸带内侧向潜流交换的研究则进展相对较慢,并且大多针对稳态条件。Brunke等[6]在研究河水与地下水交换对生态系统的重要性时提出了侧岸潜流带的概念,同时引入“潜流走廊”模型,阐述潜流与河岸带生态影响间的关联性。相较于河床潜流交换,侧岸的潜流交换更加显著[7],同时在弯曲河流上侧向潜流交换量级和范围更大[8-10]。Cardenas[8]研究了在河水补充地下水和地下水排泄到河水2种情况下,不同弯曲程度的河流侧岸潜流带范围。一方面随着河道弯曲程度的增加,侧岸潜流带的范围有所增加;另一方面随着河岸带基流流量增加,潜流带范围有所减小。林俊强等[9]通过搭建室内模型研究了不同弯曲河岸形态影响下的侧岸潜流交换特性,发现随着河岸弯曲程度增大,河岸侧向孔隙对流引起的侧岸潜流交换强度增加。
近年来,部分研究者对于非稳态的侧岸潜流交换过程进行了探索。一些学者提出了不同季节月份、水位波动、融雪等因素[11-16]作用下河岸带地下水和河水的动态交换规律。刘东升等[11]在新安江大坝下游河段监测了水压和温度,分析了冬季和夏季河岸带水热交换特征,得出夏季的潜流宽度更大;束龙仓等[13]统计了新汴河多年河岸地下水位,发现随离岸距离增加,地下水位与河道水位相关性下降。相较于长时间的潜流交换,一些学者侧重于研究短时间内河道水位急剧涨落的影响,分析了暴雨、洪水及大坝泄水等因素[17-22]影响下的河岸带地下水过程。Liang等[19]基于二维Boussinesq方程,研究了洪水事件下的顺直河岸内河水-地下水交换。结果表明,洪水期间河水快速下渗到含水层,并且大部分河水短时间内能返回河流,剩余河水将在含水层内停留很久,不仅会流回河流,也会流向下游含水层。张泽宇等[20]在室内搭建模型研究了单峰脉冲洪水信号对河岸带地下水过程影响,说明河岸带内各点地下水水位的波动随洪峰的增大而增强,水位的增幅随洪水历时的增长而增大。以上研究没有考虑到分层土体的渗透特性对地下水流动的影响。Salehin等[23]则结合水槽试验和数值模拟分析了非均质河床对潜流交换的影响,发现相较于均质河床,非均质河床潜流交换通量更大。胡淑蘅等[24]考虑了河底淤泥层及堤岸对侧向潜流的影响,结果表明两者对侧向潜流过程均有限制作用,潜流范围缩小。
目前对于长江中游干流河岸带的侧向潜流研究相对较少,多数研究集中于小流域内的局部河段内。本文通过野外原型监测和数值模拟计算,分析长江中游二元结构河岸土体的渗透特性,计算中游石首河段河岸带地下水位变化过程,给出河水变动对地下水位的主要影响范围及水量交换过程,以揭示河岸带地下水位动态变化的控制因素。
1 研究区域水文地质条件
1.1 河段概况
本文选取长江中游的石首弯道段作为研究对象(图1),研究河段位于长江中游下荆江河段,上起新厂(荆82),下迄荆104断面,全长约33.9 km,由上、下2个顺直段和1个弯道段组成,曲折系数为2.09。河段进口处较为顺直,弯道放宽段有倒口窑和藕池口心滩,弯顶左岸一侧为向家洲边滩。河段平滩河宽沿程先增加后减小,变化范围在730~2 800 m之间不等[25]。河段水面纵比降较平缓,2021年内平均纵比降为0.5。

图1 荆江河段示意Fig.1 Sketch of the Jingjiang reach
由于石首河段除进口有藕池口分流外(流量较小,约占干流流量的5%),并无其他大支流,故监利站资料可较好地代表该河段的水沙过程。三峡工程运用后的2003—2019年,监利站年均径流量为3 768亿m3,较运用前(1998—2002年)减少了6%;而年均输沙量为0.79亿t,较运用前大幅度降低,减幅为78%。此外,监利站多年平均汛期水量在运用后降低至3 005亿m3,较运用前的3 480亿m3偏少约14%,汛期来水量变化相对较小;而在上游水库蓄水拦沙及水土保持工程的综合影响下,监利站多年平均汛期输沙量在运用后显著降低至0.68亿t,较运用前的3.36亿t偏少约80%。
1.2 河岸及河床土体组成
荆江段河岸多为上部黏性土体及下部非黏性土体组成的二元结构河岸,其上层多为粉质黏土和壤土;下层为粉细砂,且下层的厚度一般大于30 m。本研究在下荆江石首河段左岸向家洲钻孔取土,得到了地表以下0~45 m的河岸土体样本,并采用激光粒径分析仪(Microtrac S3500)进行测量,得到了不同深度下河岸土体级配和中值粒径。根据测量结果,土样级配在深度4~5 m处发生明显变化,上层土体中粒径小于0.10 mm组分的含量达95%,属于黏性土类,平均中值粒径小于0.03 mm;下层土体粒径大于0.10 mm组分的含量约60%,为粉细砂,平均中值粒径为0.11 mm(图2)。河床土体组成与河岸下层土体均为粉细砂,且随着深度的增加,砂土的密实性增加。由于采样的土壤在钻孔过程中受较大干扰,因此,无法测量其他土体特性,如渗透系数等。根据之前的荆江段河岸土体土工试验结果可知,上层粉质黏土的渗透系数约为1×10-5cm/s,下侧粉细砂的渗透系数在2.4×10-3~3.8×10-3cm/s之间[26]。

图2 石首段河岸土体组成Fig.2 Bank soil compositions in the Shishou reach
1.3 河岸内部地下水位监测
2021年1月19日至11月28日,在向家洲(29°45′01″N,112°23′32″E)和北门口(29°45′16″N,112°26′01″E)2个站点布置了3口监测井(图1、图3),测得了2处地下水位的变化过程。在向家洲河岸离岸10 m和20 m处修建了2个监测井(1号井和2号井),在荆95断面上游约800 m处;在北门口离岸10 m处修建了3号井,在荆98断面上游约700 m处。3口井的深度均为20.0 m,井底高程比最低河道水位低约9.0 m。每口井的顶部高出地表1.2~1.4 m,以确保井在洪水漫滩时不被淹没。每口井内悬挂一台HOBOU20-001-02水位记录仪,测量范围为0~30.5 m,测量精度为0.03 m。水位记录仪固定在地表以下16.2~16.4 m处,比最低河道水位低约5.0 m。

表1 土体渗透系数率定结果Table 1 Calibration of the hydraulic conductivity of bank soil

图3 地下水位监测井布置情况Fig.3 Setup of the groundwater level monitoring wells
图4给出了2021年1月19日至11月28日内3口监测井的地下水位、石首水位站的实测日均水位及降水量。2021年石首站的最高水位为34.17 m,最低水位为24.53 m,平均水位为29.19 m。在1—3月间始终保持较低水位,之后在4—6月水位抬升,7月进入洪峰期,并于9月中旬达到最高水位。在三峡工程开始蓄水后,水位开始下降,平均日退水速率约0.12 m/d。根据降雨过程可知,石首河段2021年降水量为1 374.0 mm,主要降雨时段集中于4—8月,其中4月7日、4月24日、6月3日和8月24日降水量大于40.0 mm。相较于多年平均值,2021年属于偏丰水年。日均降水量与石首站水位相关系数约为0.10,可见该地水位主要受上游来流控制,受局地降雨影响较小。

图4 2021年河道水位、地下水位和降水量变化过程Fig.4 Temporal variations in the river stage,groundwater level and rainfall in 2021
北门口(3号井)离岸10 m处的地下水位与河道水位同步性强,水位峰值均出现于同一天。在涨水期和洪峰期内,该处地下水位与河道水位平均差值约为0.21 m。向家洲(1号井、2号井)实测的地下水位在4月8—16日、4月22日至5月1日、5月22日至6月7日之间存在陡升陡降的现象,在后文(3.4节)中分析了造成该现象的原因,判断可能与该区域附近水塘的修建和蓄水有关。除去这几日的数据外,1号井的地下水位与3号井的水位十分接近。而离岸20 m处(2号井)的地下水位同步性下降,最高水位落后河道水位1 d,峰值下降约0.12 m。在退水期内,3口井的地下水位明显高于河道水位,最大水位差约1.42 m,反映了地下水位的滞后性。
2 侧向潜流过程计算模型与验证
2.1 地下水三维运动方程
在不考虑水的密度变化条件下,孔隙介质中三维空间的流动可以用下面的偏微分方程表示:
(1)
式中:Kxx、Kyy、Kzz为渗透系数在x、y和z方向上的分量,m/s;h为水头,m;W为单位体积流量,s-1,用以代表流进汇或来自源的水量,由降雨或其他因素形成;ss为孔隙介质的储水率,m-1;t为时间,s。模型构建及求解使用MODFLOW数字模型[27],其数值求解方式使用有限差分法。
2.2 局部模型率定与验证
2.2.1模型率定
模型率定过程中的计算区域选择在荆98断面局部河段,河段内设置有北门口站点3号监测井(图3),利用所测地下水位对渗透系数进行率定。荆98断面位于弯顶下侧(图1),左岸为凸岸侧,河底坡度较缓;右岸为凹岸侧,河底坡度较陡。凸岸侧有边滩,中水时露出,洪水时淹没。
模型横向计算范围为6 000 m,断面地形采用2019年的实测数据。由于河漫滩高程变化相对较小,故忽略其河漫滩的地形变化,近似可取为河道最外侧高程实测值。垂向上,该断面地表以下70 m为不透水基岩[28],故本次模拟范围上至河底及河岸表面,下至-70 m深度。纵向上沿荆98断面上下游各延伸500 m。计算的网格总个数为10×401×23(纵向×横向×垂向)。网格纵向尺寸为100 m;横向尺寸为20 m,靠近河道附近的网格加密,缩小为10 m;垂向尺寸介于0.9~6.9 m,且位于浸润线附近的网格较密。
根据实测资料,河岸组成由上到下依次为4~5 m粉质黏土、16~20 m松散-稍密粉细砂、20~25 m中密粉细砂、55 m密实粉细砂,底部为不透水基岩;河床组成由上到下依次为8~20 m松散-稍密粉细砂、8~25 m中密粉细砂、55 m密实粉细砂,底部为不透水基岩。各土层渗透系数取值范围参考《水利水电工程水文地质勘察规范:SL373—2007》,同时结合以往的实测资料,表1给出了渗透系数率定结果。
计算区域内的边界条件设置为:① 纵向边界上,由于局部河段内上下游水位变化很小,纵向坡降引起的河岸内地下水上下游流动可忽略不计,即假设上下游流量为0 m3/s;② 横向边界上,河岸横向最外侧赋予河道最低水位24.53 m,河道边界赋予石首站的实测日均水位条件(图4);③ 垂向边界上,底部设置为不透水边界。在模型率定与验证中,暂不考虑降雨影响,则源项为0。
图5给出了北门口地下水位监测点3号井计算与实测的地下水位过程对比情况。从图5中可以看出,整体上计算结果与实测地下水位过程吻合较好。在涨水过程中,模拟结果与实测结果吻合性良好,平均绝对误差约为0.20 m,纳什效率系数大于0.99;退水过程中模拟结果和实测数据间误差略有增大,平均误差约为0.32 m。

图5 北门口3号监测井计算与实测的地下水位Fig.5 Calculated and measured groundwater level hydrographs in the No.3 well
2.2.2模型验证与敏感性分析
利用向家洲布置的2个地下水位监测井(1号井和2号井,图3),对模型进行验证。向家洲位于荆95断面附近,模型构建过程与前面相同,且同样采用石首水位站的实测值作为边界条件(图4)。由实测资料可知,向家洲处河岸上层为粉质黏土,厚度约为4 m,下侧为粉细砂。各层土体的渗透系数取值与表1相同。
图6给出了向家洲监测点计算与实测的地下水位变化过程。除去几处水位骤增数据外,在离岸10 m处地下水位的计算值与实测值的绝对误差多在0.23 m以内,但在退水期末误差较大,误差约为0.60 m;在离岸20 m处,地下水位的计算值与实测值的误差多在0.33 m以内。
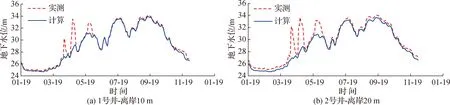
图6 向家洲监测点计算与实测地下水位过程Fig.6 Calculated and measured groundwater level hydrographs at Xiangjiazhou
以向家洲处的地下水位变化为研究对象,开展了河岸渗透系数的敏感性分析。对于表层黏土,在表1的渗透系数取值基础上(工况1)分别增加和减小50%(工况2、工况3),开展潜流过程计算。对比离岸20 m处的地下水位过程,工况1—工况3的地下水位相差很小,差值小于0.02 m。对于下层粉细砂的渗透系数,结合实测资料设置计算工况4—工况6,对应的渗透系数分别为0.002 5、0.005 0和0.007 5 cm/s。图7(a)给出了在离岸20 m处,不同渗透系数下计算的地下水位变化过程。可以看出,河岸下层粉细砂层对于地下水位计算结果的影响较大,当渗透系数减小至0.002 5 cm/s时(工况4),涨水期及洪峰期地下水位较工况5降低了0.19 m,退水期增加了约0.11 m;当渗透系数增加至0.007 5 cm/s时(工况6),涨水期及洪峰期地下水位较工况5增加了0.05 m,退水期则降低了约0.09 m。进一步分析下层粉细砂渗透系数变化对单位河长内的河水-地下水交换量的影响,如图7(b)所示。当渗透系数减少至0.002 5 cm/s时,河水补充地下水峰值减少27 m3/(m·d),地下水排泄河水峰值减少14 m3/(m·d),全年内河水补充地下水减少约1 000 m3/m,地下水排泄河水减少约1 000 m3/m。;当渗透系数增加至0.007 5 cm/s时,河水补充地下水峰值增加10 m3/(m·d),地下水排泄河水峰值增加22 m3/(m·d),全年内河水补充地下水增加约1 500 m3/m,地下水排泄河水增加约1 000 m3/m。

图7 下层粉细砂不同渗透系数下离岸20 m处模拟结果Fig.7 Simulation results at 20 m distance from the bank slope with different hydraulic conductivities of fine sand
总体看来,河岸表层粉质黏土渗透系数的改变对河岸地下水位的影响较小,而下层粉细砂渗透系数的改变对地下水位及潜流量的计算结果影响较大,且离岸越远影响越明显。由于表层土体较薄,2021年内河道水位高于表层土体底板的历时约有80 d,故大部分时间段内表层黏土对地下水位的影响较小。将表层黏土的渗透系数与下侧粉细砂设为一致,地下水位的计算结果仅改变了0.3%,同时若忽略粉细砂因密实度增加产生的渗透系数变化,计算结果的影响在2%以内。因此,在后续河段尺度的潜流过程研究中,可近似不考虑河岸土体分层对于潜流过程模拟的影响。
2.3 河段模型建立与验证
断面局部模型模拟计算时,主要分析了单侧河水对河岸地下水的作用,没有考虑到平面地形变化对侧向潜流的影响[29-30]。而在实际河流中,弯曲河流常常拥有蜿蜒的河岸形态,河岸会受到多侧河水的入渗;同时在河岸带内地下水间也会相互作用,对地下水的时空变化分布产生进一步影响[19]。为了分析河流平面形态对侧向潜流范围的影响,此处在上述分析的基础上,进一步扩展了平面计算范围。通过分析河弯内不同位置潜流过程的差异,揭示河道形态变化对河岸带地下水位的影响。
2.3.1模型建立
石首河段模拟范围长13.55 km、宽10.8 km,范围内河道长度为33.9 km,曲折系数为2.09(图1)。模拟网格共216列、271行,总网格数量为58 536个,河道处网格作为无效网格处理,共7 249个,故有效网格数为51 287个,每个网格的长度和宽度均为50 m。由前文参数敏感性分析可知,下层粉细砂的渗透系数对计算结果的影响远大于表层粉质黏土。本研究缺乏区域内全部的河岸土体分层资料,难以建立全范围内非均质河岸模型,故近似采用均质河岸模型,则区域内土体均采用粉细砂层的渗透系数(0.005 0 cm/s)。针对边界条件,在河道两侧网格赋予水位条件,模拟范围四周边界采用零流量边界条件。根据长江水利委员会水文局荆江水文水资源勘测局实测资料,河弯左右两岸的水位差在0.02~0.08 m之间,横比降约为0.05%,左右两岸水位差相较于约7.7 m的河道水位年变幅很小,对河岸带地下水位计算结果影响很小,故可利用新厂和石首站的水位插值赋予沿程水位条件。
2.3.2模型验证
对比荆95断面局部模型离岸50 m处地下水位与石首河段模型同位置处的地下水位。整体上河段模型计算地下水位略高于局部模型计算水位,平均高约0.42 m,涨水期和洪峰期内平均水位差约0.46 m,而在退水期平均水位差减小约0.31 m。计算时间段内,纳什效率系数约为0.98,说明河段模型计算结果较为准确,而水位略高于局部模型原因可能在于河流平面形态的影响。
3 典型急弯段侧向潜流模拟分析
3.1 单侧河水作用下的侧向潜流范围与潜流量
将荆95断面局部模型计算时段扩大至2021年全年,图8给出了初始时刻(1月1日)、河道水位最高时(9月10日)、计算时段末(12月31日)的河道水位及地下水位横向变化。对比初始水位线和最高水位线,地下水位横向梯度在涨水的过程中明显增大。相较于初始河道水位26.45 m,洪峰期内河道的最高水位达34.17 m,增加了7.72 m。近岸处的地下水位随河道水位提升明显,两侧离岸100 m内地下水位增加幅度超过6.0 m,离岸200 m内的增加幅度超过4.5 m。远岸处的地下水位受河道水位的影响较小,在左右岸离岸800 m外,地下水位较初始情况的增加幅度小于1.0 m。在退水期内,河道水位下降,但远岸处的水仍然流向河岸内部,地下水位有所提升,使得潜流带范围仍有所扩大。在左右岸离岸约1 400 m外,地下水位变幅小于河道水位变幅的5%,故河道水位波动对该范围以外的地下水位变化的影响很小。

图8 河道水位及地下水位线横截面Fig.8 Lateral profiles of river stage and groundwater level
图9给出了单位河长内的河水-地下水交换量与河道水位变化过程。从图9中可以看出,单位河长内河水-地下水交换量的变化趋势大致与河道水位同步,在河道水位较高时,河道补充地下水的水量较大;当河道水位较低时,河道水补充地下水的水量较小,且当河道水位持续下降时,地下水反过来排泄到河道。在单位河长范围,2021年内河道补充地下水的水量约为5 000 m3/m,地下水排泄河道水量约为3 000 m3/m,净水量约为2 000 m3/m。2021年监利站径流量为4 228亿m3,沙市至监利站距离为162 km,河段内河水向河岸入渗的净水量约为6.5亿m3,约占监利站径流量的0.15%。

图9 荆95断面附近单位河长内河水与地下水的交换水量与河道水位变化过程Fig.9 Temporal variation of the water exchange volume between river and groundwater per channel-length and the river stage at the section of Jing 95
3.2 石首河段地下水位分布特征及潜流量
图10(X为横向起点距,Y为纵向起点距)给出了石首河段不同时刻河岸地下水位的分布情况。初始时刻地下水位与河道水位相差很小,无明显水流流动(图10(a))。在涨水过程中,河岸带的地下水位随着河道水位不断抬升。当河道水位达到最高时(图10(b),9月10日,河道水位为35.05~33.61 m),河岸带一定范围内地下水位有了明显提升。河道水位较初始情况增加7.62~7.71 m,近岸处的地下水位涨幅较大,在距河道100 m河岸内,地下水位较初始情况增幅大于6.5 m;远岸处地下水位涨幅较小,距河道900 m河岸外,地下水位较初始情况增幅小于1.0 m。
在河道水位经历短暂下降后(图10(c),10月20日),一方面近岸处的地下水位对河道水位变动敏感,也立即随之下降,地下水来不及传入河岸内部而排泄入河道中;另一方面,远岸处的地下水位仍在增加。此时,相较于最高水位,河道水位下降了4.07~3.96 m,但是600 m外的地下水位仍然在上升。地下水水位波峰传达至离岸约300 m处,水位呈现出中间高、两边低的情况,地下水一方面会补给河水,另一方面会继续往河岸内部流动。经历1 a的模拟后(图10(d),12月31日),河岸带的地下水位分布情况较初始水位有了明显变化。河道水位全年内最大变幅约为7.7 m,而在1 600 m外,在全年内水位变幅小于河道水位最大变幅的5%,河道水位变动基本不影响该处的地下水位。
对比局部模型与河段模型,在考虑了河流的平面形态后,侧岸潜流的主要影响范围有所扩大,原因在于河岸带内上下游的河水入渗促进了潜流向内发展,特别在凸岸处,地下水位明显较高。对比潜流量,取荆95断面所在位置,在单位河长范围,2021年内河道补充地下水的水量约为5 000 m3/m,地下水排泄河道水量约为3 000 m3/m。相较于前文所计算的水量较为相似,原因在于河道内水体主要位于黏土层之下,故前文计算结果中河水通过黏土层向内入渗仅占很小一部分。
3.3 不同河流形态特征位置的地下水位变化过程
为了研究2021年内河流平面形态变化对于河岸带地下水位的影响,选取弯道进口顺直侧、弯道凸侧等4个具有不同形态的河岸位置(研究位置A—D,图10(a)所示),分析不同离岸距离下地下水位的变化过程。该4处位置分别具有的特点包括:① 弯道进口顺直侧,该处河岸单侧临水;② 左岸凸侧,该处河岸两侧临水;③ 右岸凹侧,同样受到两侧河道水位影响;④ 洲滩处,地下水受四周河水影响。图11(a)给出了进口顺直段(位置A)离岸距离(S)分别为100、500、1 000 m处的地下水位变化过程。如图11(a)所示,在离岸100 m处的地下水位和河道水位的相位差较小,具备较好的跟随性,对河道水位响应较快;但随着离岸距离的增加,地下水位与河道水位之间的相位差增大。在离岸500 m处,地下水整个水位过程只有一次涨落过程,且最高水位时刻(10月17日)滞后河道37 d,而当距离达到1 000 m时,水位变化过程只有较平缓的涨水过程,变化幅度更小。同时从图11(a)中可以看出,随着离岸距离的增加,地下水位的涨退历时也在明显增加。河道水位在1月2日至2月19日有一个短暂的上升回落过程,在离岸500 m处,这个过程坦化,上升回落时间为1月2日至4月3日,历时93 d,相较于河道(历时49 d)增加44 d。而在离岸1 000 m处,河道水位短暂上升对地下水位已无影响(水位变化小于0.01 m)。在退水期,离岸500 m处地下水已经不能在12月31日前完成退水过程,但进入下一年份的枯水期(1—3月),水位可能会继续下降。

图11 不同河流形态特征处河岸地下水位过程Fig.11 Groundwater level at different location with different morphological characteristics of rivers
在弯道凸岸侧(位置B,图11(b)),相较于顺直段,随着离岸距离的增加,也会出现峰值坦化,历时增长的情况;但是在退水过程中,各距离下的地下水位要明显高于顺直段的地下水位。相较于单侧河水影响的顺直段,处于弯道凸侧的河岸会受到两侧河水的同时入渗,涨水时地下水位抬升更快,且地下水位峰值也更高。而在弯道凹岸侧(位置C,图11(c)),地下水位在上升和下降时,都更加缓慢。凹岸受到地形的影响,使得在垂直河岸相同距离下的点,两侧河水的入渗河岸流路更长,使得其地下水位响应时间更久,这与凸岸的情况相反。洲滩(位置D,图11(d))的地下水位对河道水位的变化最为敏感,相较于前3种情况,两者之间的相位差最小。由于受到四周河水的同时入渗,导致其地下水位响应最快,离岸相同距离下地下水位抬升更快,峰值更高。
3.4 考虑降雨的地下水位变化过程
在前文的数值模拟中,着重于分析河道水位变动对地下水位的影响,从而忽略了降雨下渗部分,现将2021年石首降水量(图4)考虑至模型。根据徐苏等[31]提出的径流系数(μ)计算公式,考虑了计算区域内的下垫面条件和年降水量,计算出径流系数μ=0.80。则降雨下渗部分的水量为降水量的0.2倍。考虑降水量之后,对荆95断面局部河段的地下水位变化过程再次进行计算。对比发现,考虑降雨后离岸10 m和20 m处的地下水位分别提高0.05 m和0.09 m,变化差别很小。同时利用Pearson相关系数法分析了该2处的地下水位与降水量的相关系数,分别为0.02和0.03,而与河道水位的相关系数达到了0.98和0.97,地下水位受河流影响显著,河道水位对地下水位动态起主要控制作用[32]。另一方面,在8月24日也见较大降水量,但未见地下水位突然抬升,再对比了其他文献中地下水位数据[11,14,19],也未出现短暂时间内因降雨导致河岸带地下水位大幅度提升的情况。综合以上看来,向家洲处监测井在4月8—16日、4月22日至5月1日、5月22日至6月7日之间地下水位存在陡升陡降的现象,并非因为降雨而造成,可能与该区域附近水塘的修建和蓄水有关,或是其他人为因素造成的。
在考虑降雨后,河岸带内的地下水位有所提升,但是水位变幅相差很小,与前文所得结论几乎一致。但是地下水位的抬升,对流入流出河岸的水量影响较大,在单位河长范围,2021年内河道补充地下水的水量约为4 000 m3/m,地下水排泄河道水量约为4 000 m3/m,两者几乎相等。河岸带地下水位抬升,在河道水位高时,降低了水力坡降,使得河道补充地下水的水量减少;相反,在地下水位高时,提高了水力坡降,使得地下水排泄河道的水量增加。
4 结 论
本文基于2021年石首段河岸开展的土体级配测量与地下水位监测结果,采用MODFLOW模型对荆江石首河段的侧向潜流过程进行了模拟,利用实测数据对模型进行了率定与验证,揭示了年内变动河道水位影响下河岸内部地下水位的时空变化规律,并确定了该年侧岸潜流的主要影响范围。主要结论如下:
(1) 河岸带地下水位动态变化主要受河道水位控制,近岸处水位变化同步性强,伴随离岸距离的增加,地下水位的涨退水过程坦化,历时增长,且峰值下降,对河道水位变化的响应滞后性增加。河道水位全年最大变幅约7.7 m,离岸10 m和100 m处地下水最大变幅分别约为河道水位变幅的96%、80%,峰值分别低约0.1 m、1.5 m。研究区域内侧岸潜流影响范围在离岸约1 400~1 600 m内,更远处地下水位年内变幅小于河道水位最大变幅的5%。
(2) 河水-地下水交换水量受河道水位与降雨入渗共同影响,河道水位持续抬升(下降)时,地下水与河水间的水力坡降增加,交换水量较大。不考虑降雨入渗影响时,全年河道补充地下水的水量约为5 000 m3/m,地下水排泄河道水量约为3 000 m3/m。考虑降雨入渗后,河岸带地下水位有所提升,水力坡降在较高(低)河道水位时降低(提高),全年河道补充(排泄)地下水的水量均约为4 000 m3/m。
(3) 不同河流形态特征下的河岸带地下水位过程存在差异,相较于顺直段,弯道凹岸离岸相同距离处的地下水位响应更慢,且峰值更低,其原因在于凹岸受平面地形影响,两侧河水入渗河岸流路更长;凸岸则相反。洲滩处受到四周河水同时入渗,地下水位响应最快,峰值最高。

