珠江三角洲顶点思贤滘分流自适应调节机制
袁 菲,陈文龙,胡晓张,卢 陈,高时友,黄鹏飞
(1. 珠江水利委员会珠江水利科学研究院,广东 广州 510611;2. 水利部珠江河口治理与保护重点实验室,广东 广州 510611)
分汊河道在三角洲河网区是一种常见的河流平面形态,分流比是分汊河道的一个重要参数,其大小和变化决定河网区各支汊的兴衰[1-2],影响航道变迁、防洪情势、环境生态等诸多方面[3-4],开展自然与人类活动作用下的汊道分流机制研究具有重要的理论意义和实践价值。天然情况下,影响汊道分流的因素很多,如分流角[5]、分流口形状[6]、各汊道的地形变化[7]和来水来沙条件[8];人类活动干扰下的地形下切被证明对汊道分流有至关重要的影响[9-10];感潮河道内的潮波运动也是汊道分流的影响因素之一[11-12]。河道水流分配正是诸多因素间相互影响、相互调整结果的综合反映。
在珠江三角洲一级分流节点思贤滘,几十甚至上百年来都维持着稳定的X形汊口格局,受上游洪水、外海潮汐、平面形态、河床地形及地质等多因素的相互作用,思贤滘分流存在动态调整,并在一定程度上调控着下游河网动力及地貌演变[13-14]。目前,学者们对思贤滘分流的研究主要集中于分流年际变化特征,杨清书等[15]发现思贤滘的分水分沙格局自1993年后发生了重大变化,三水站分流分沙比显著增大;张灵等[16]认为水沙变异时间在1992年前后,并讨论了其负面影响,认为北江分流加大会导致三角洲腹地水位抬升。部分学者探讨了汊口地形变化对分流的影响,刘幼萍[17]对水文、地形成果分析,发现河床形态的重大变化导致西、北江分流比由1959—1989年的85∶15变为1989—2017年的80∶20;陈小齐等[18]分析认为21世纪以来西江地形下切幅度大于北江,地形不均匀下切导致西江分流增加2%。王博芝等[19]提出思贤滘分流还受余水位坡度、潮波衰减率等径潮动力的调节作用。由此可见,对于思贤滘分流规律及其变化原因的探讨目前还以定性分析及数据统计研究为主,对思贤滘分流比影响因素的认识仍不系统,对分流机制的研究及理论的探讨还较为匮乏,思贤滘作为珠江三角洲“牵一发而动全身”的关键节点,其分流规律及机制还需要进一步研究。
珠江三角洲不仅径潮动力复杂,且思贤滘形态为罕见的X形交叉口,进一步加大了问题的复杂性。本文结合资料分析、物理模型、数学模型及理论分析等方法,分析思贤滘分流的自适应调节规律,探讨X形潮汐汊口的分流机制,丰富感潮型分汊河道的分流理论研究,研究成果以期为河口三角洲的防洪、供水安全及水生态环境保护提供理论指导与决策建议。
1 研究区域概况
珠江三角洲形态呈“三江汇流,八口出海”格局(图1)。其中,“三江”分别为西江、北江和东江,西江、北江于广东省三水思贤滘相汇后注入西北江三角洲,东江于东莞市石龙镇汇入东江三角洲。
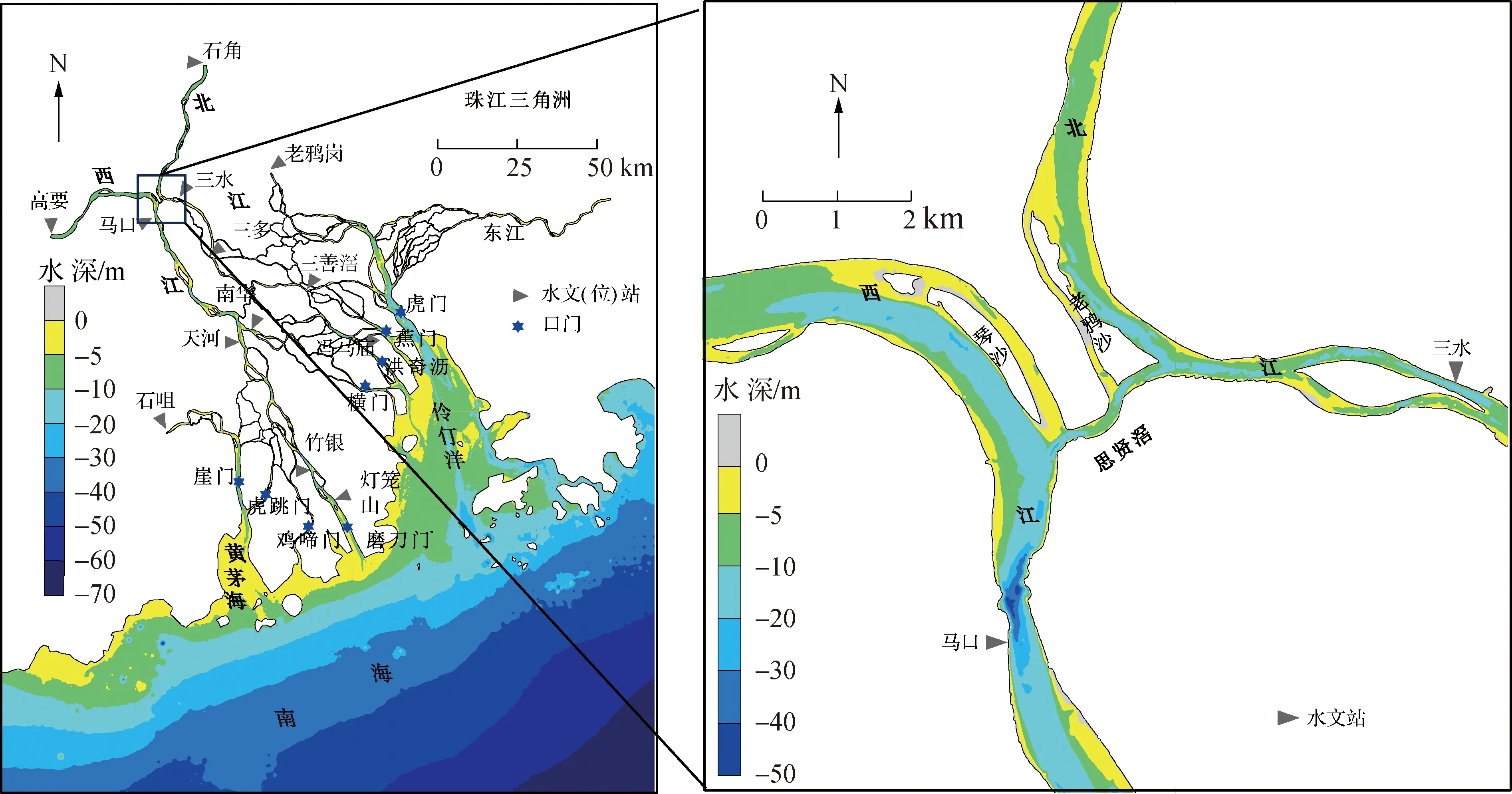
图1 研究区域Fig.1 Study area
西江和北江是珠江的两大重要水系,思贤滘为两江相连之处,是珠江三角洲上沟通西、北两江的第一条汊道。西、北江来流在此经过重新分配后折头南下,随后经河网各级支汊,通过八大口门入海。马口、三水水文站分别位于思贤滘西、东汊口,是西、北江下游的主要控制站。在平面上,思贤滘区呈X形,并且在几十上百年来维持着稳定的X形主支汊地貌形态格局。
2 资料收集与研究方法
2.1 资料收集
本文收集思贤滘区1999年、2005年和2020年3套地形数据,资料来自中水珠江规划勘测设计有限公司提供的水下地形测量成果;收集马口、三水断面20世纪60年代以来共7套断面地形数据,资料来自珠江水利委员会历次水文测验的实测大断面成果;收集马口、三水站1959—2017年逐日流量数据,马口、灯笼山、三水、冯马庙站年平均水位特征值,数据来自《珠江流域水文资料》年鉴;收集珠江流域2005年6月及2006年7月洪水期水文资料,数据来自珠江水利委员会提供的特大洪水水文测验成果。
2.2 研究方法
2.2.1数学模型
建立包含珠江河网区及河口湾区的潮流数学模型(图2(a)),模型的计算范围是112°12′E—114°54′E,21°12′N—24°48′N。模型有5条上游开边界,分别是潭江的石咀、西江的高要、北江的石角、溪流河的老鸦岗和东江的博罗,外海开边界为45 m等深线处。模型采用1999年地形成果,采用1998年6月典型洪水期的珠江河网区同步水文测验资料进行验证,主要验证三角洲河网区的水位及马口、三水流量,计算误差在10%以内,符合相关规程要求。

图2 思贤滘数学模型网格及物理模型研究范围与布局Fig.2 Sixianjiao mathematical model grid and research scope and layout of physical model
2.2.2物理模型
思贤滘局部物理模型上游边界取自西、北江弯道上游的顺直段(图2(b)),距离思贤滘约6 km;下游边界分别位于距马口站4.8 km、三水站8 km的顺直段,原型南北长约17 km,东西宽约16 km。物理模型的平面比尺为300,垂直比尺为100,变率为3。模型下边界通过H—Q(水位—流量)关系控制,采用溢流堰确定H—Q关系使之与原型基本一致。工程后的流量变化则通过量水堰直接测得。采用2020年6月小洪水进行模型率定,采用2005年6月大洪水进行模型验证,主要验证马口、三水站水位及流量。
3 思贤滘地形演变特征
思贤滘全长约1.5 km,平均河宽250 m。滘区在平面上呈X形,西滘口跟西江干流相通,北滘口跟北江干流相接,西滘口南岸是陡直的岩质山体,其上游约500 m沙洲为琴沙,北滘口上游沙洲为老鸦沙。1999—2020年,思贤滘区河道大体呈现滩淤槽冲特征。其中,1999—2005年,思贤滘区西江侧以冲刷为主,容积增加0.07亿m3,增幅为3%,主槽最大下切超过20 m;北江侧河道相对平衡(表1,图3(a))。2005—2020年,思贤滘区西江侧总体由冲转淤,容积减少0.33亿m3,减幅为16%,滩槽分化显著,边滩强烈淤积,淤高超过5 m,冲刷主要发生在局部深槽;北江侧容积减少0.13亿m3,减幅为15%(表1,图3(b))。分析范围向下游扩展,西江下游马口至天河段总体持续冲刷,北江三水至三善滘段由冲转淤(表1)。考虑当前上游来沙趋于减少,思贤滘区的马口及三水断面河床相对稳定(图4),预计未来思贤滘下游及三角洲河道河床较为稳定,滘区地形格局不会出现大的变化。

表1 思贤滘区及下游河段容积及其变化Table 1 Volume and change of Sixianjiao area and its downstream reaches
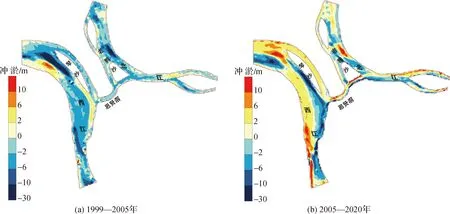
图3 思贤滘区河道地形冲淤演变Fig.3 Evolution of the terrain near Sixianjiao
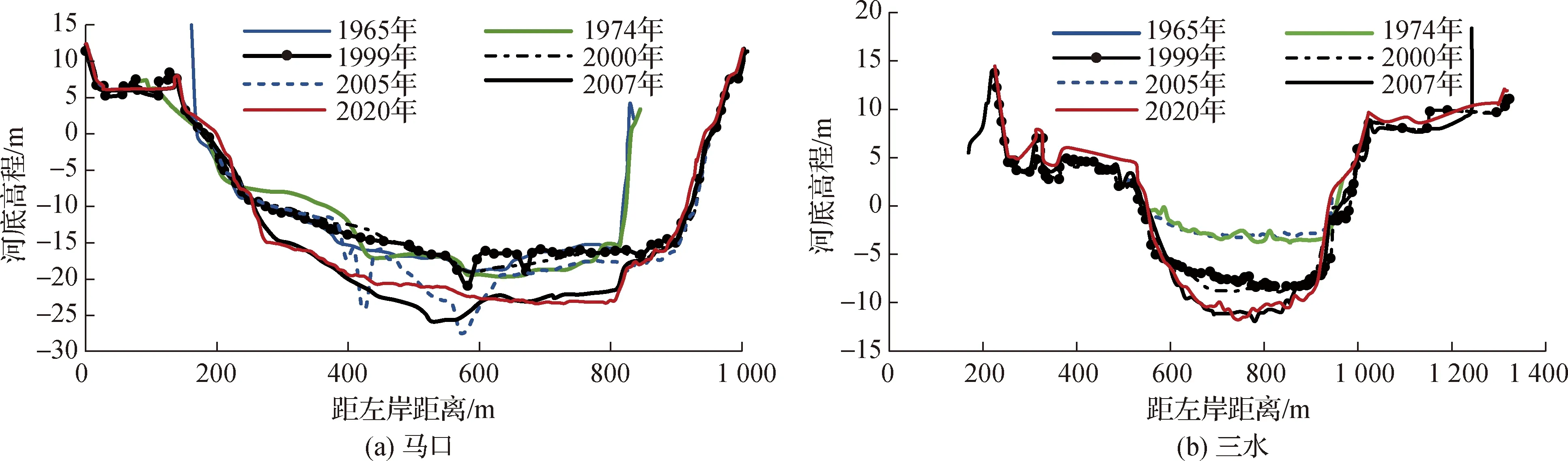
图4 思贤滘区马口、三水断面地形变化Fig.4 Terrain change of Makou and Sanshui sections near Sixianjiao
4 思贤滘分流自适应调节规律
4.1 历史分流规律
2 000多年前思贤滘附近是洲岛众多的汊河区,西江直流过滘,随着北江东迁及三角洲的推进发展,元明时期,思贤滘形成西、北江分流(西江过北江)格局;清朝,围堤修筑加速滘区变窄,发育曲流弯道,思贤滘成为分流天然调节器,水流以西江过北江为主,同时洪水也可以反过西江[20];民国以来,由于北江河床增高快,过西江水量日增,形成了北江“强支夺干”的形势;20世纪50年代,年均北江水量入西江为22%,枯水季则达70%~80%。从思贤滘过滘水流的变化可以推断,其分流形势的调整与河床的冲淤变化密切相关。
4.2 近期分流变化
20世纪60—90年代,思贤滘水流以北江过西江为主,洪季少部分时间为西江过北江。20世纪80年代以来,三角洲采砂活动频繁,思贤滘分流比不断调整。20世纪80年代至1993年,三角洲采砂主要发生在北江片区,北江三水分流比增大,西江马口分流比骤降,西江过北江流量增大;1993—2005年,西江采砂幅度大于北江,分流逐渐向西江增加;2005年以后,三角洲全面禁采,西、北江河床相对稳定,洪水分流比基本保持在78%左右(图5)。
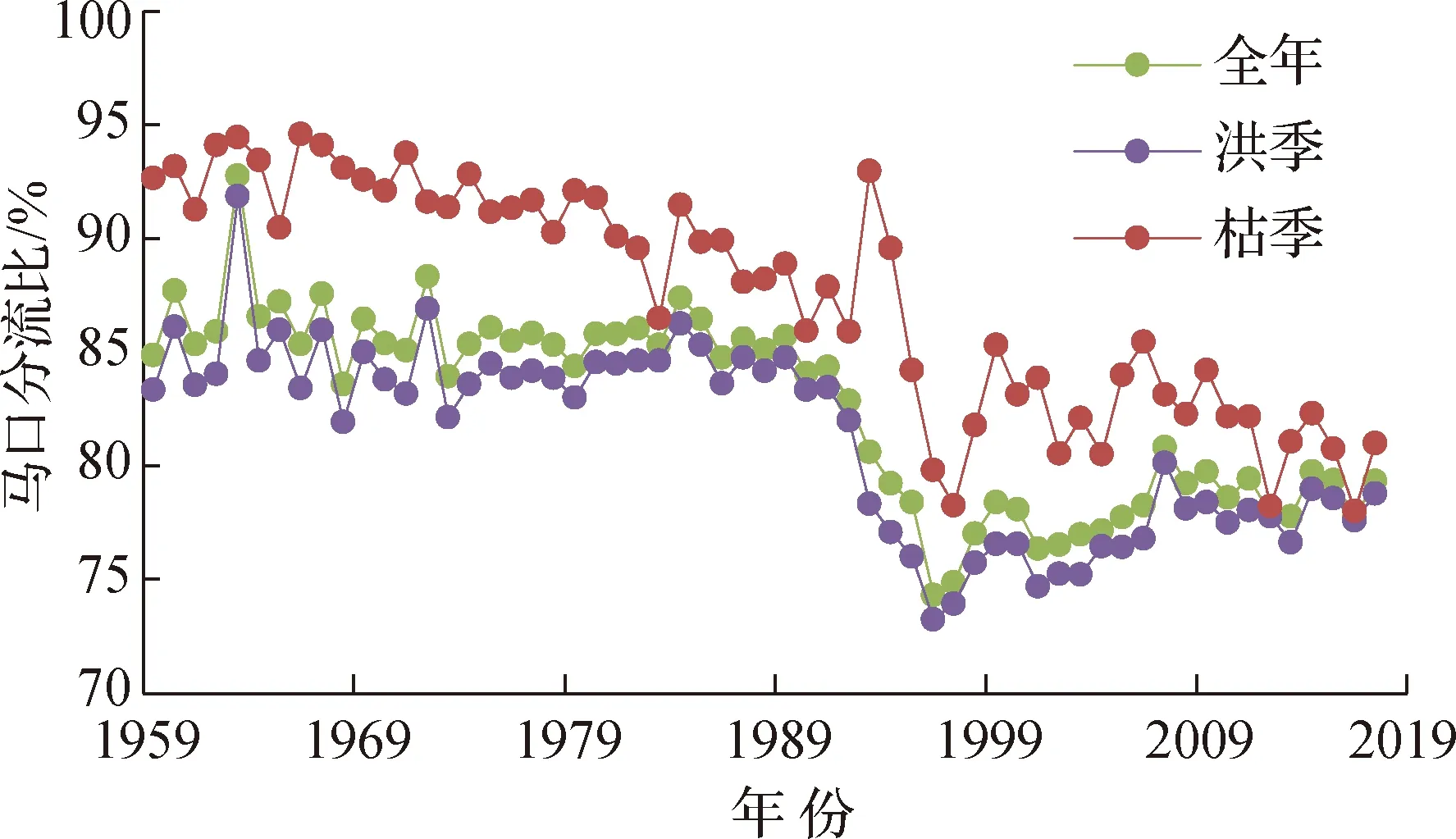
图5 马口洪季、枯季及全年分流比的年际变化Fig.5 Inter-annual change of the flood season,dry season and annual diversion ratio of Makou
4.3 分流自适应调节规律
采用马口及三水水文站逐日流量资料分析思贤滘的分流特征,见图6,上游来流量越大,三水的分流比越大;当流量达到一定阈值时,分流比趋于稳定,大洪水时三水分流比稳定在25%左右,西江马口与北江三水流量比大致为3∶1。对比20世纪90年代前与2000年后三水的分流比,地形不均匀下切致使在同等来流条件下,三水分流比增大(图6(d))。枯水期思贤滘水流受到潮汐顶托作用影响,无明显规律。
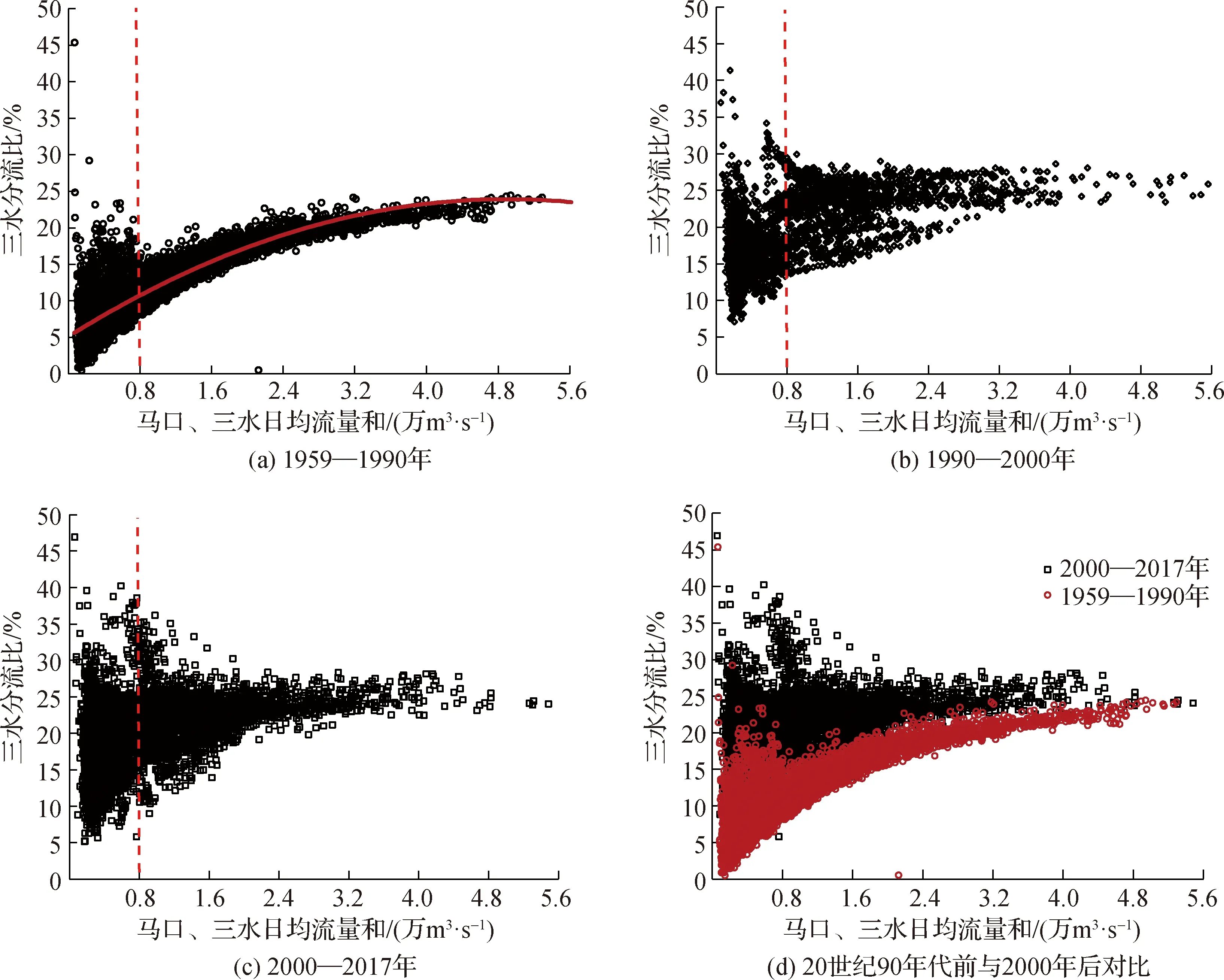
图6 各年代思贤滘日均流量与三水分流比关系Fig.6 Relationship between the daily flow in the Sixianjiao channel and the diversion ratio at Sanshui over the years
采用物理模型研究思贤滘的分流规律,模型试验结果表明(图7):① 2006年7月,北江洪水为主的试验(代号“067”)中,思贤滘上游西、北江来流比随时间不断变化,但下游分流比趋于稳定。分流前,西、北江流量比范围为1.2~7;分流后,马口和三水流量比总体稳定在3∶1。② 2005年6月,西江洪水为主的试验(代号“056”)中,洪峰时刻,思贤滘水流为西向北(图8)。2006年7月,北江洪水为主的试验中,洪峰时刻,思贤滘水流为北向西。③ 当西江洪水大于北江洪水3倍以上时,思贤滘水流为西江过北江;当西江洪水小于北江洪水3倍时,则为北江过西江。由此可见,思贤滘是一个天然的洪水调节器,具有稳定西、北江洪水分流比的作用。
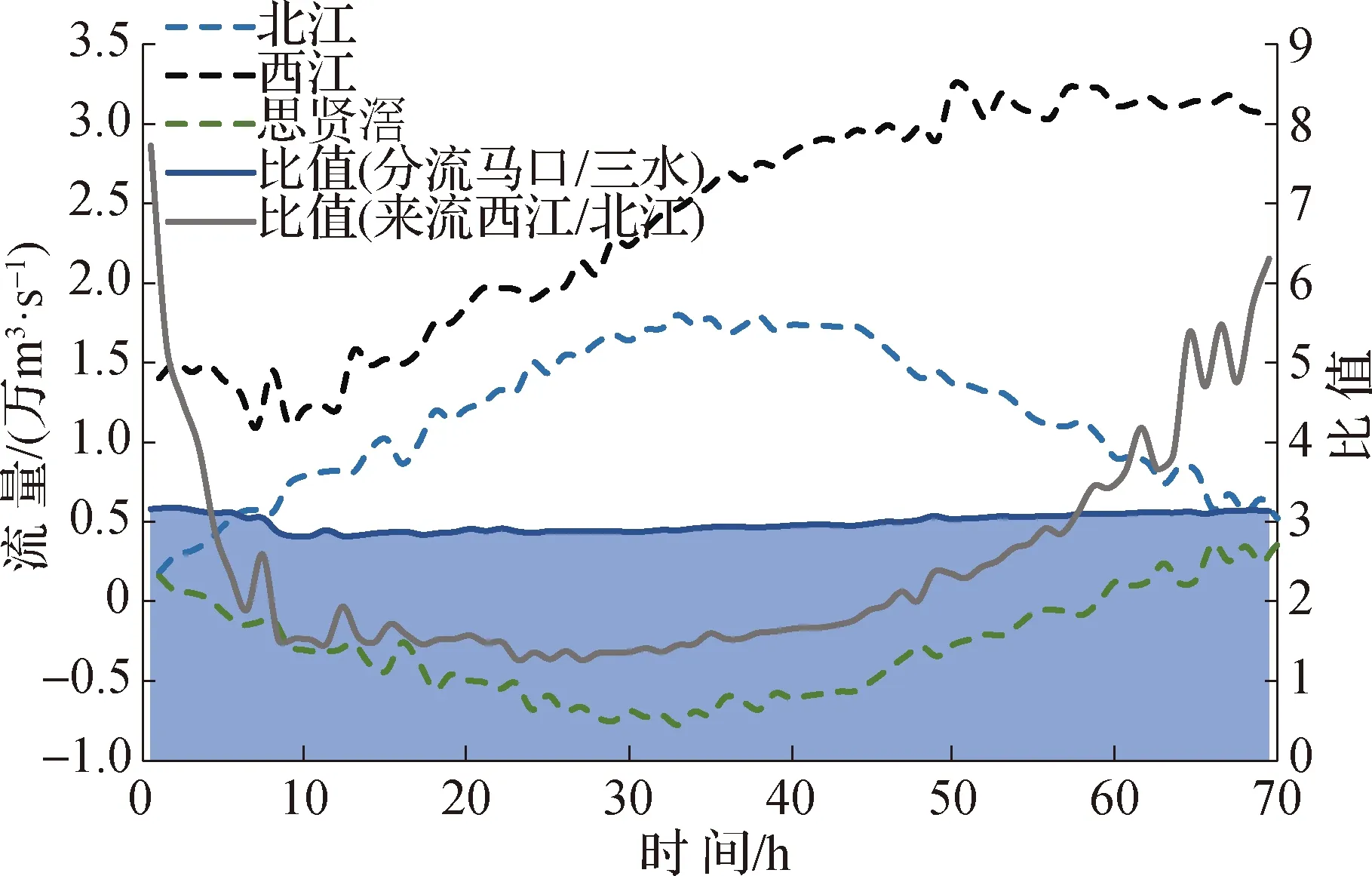
图7 物理模型试验中“067”洪水思贤滘分流情况Fig.7 Results of a physical model experiment on the Sixianjiao diversion during the typical “067” flood
5 思贤滘分流自适应调节机制
5.1 思贤滘下游地形影响
根据流量关系Q=Av,其中,Q为流量,A为过水断面面积,v为断面平均流速。对于受两岸堤防约束的河道,其断面往往呈不规则“U”型形态,断面的上部水面宽趋近于常数,水位—面积关系曲线近于直线。当水位变化dZ时,面积相应变化dA,水位—面积关系曲线的斜率与河宽(B)之间有如下关系:dA/dZ=B。对两边同时积分可得,A=BZ+a,其中,a为堤防以下不规则的河床断面面积,BZ为由堤防约束的规则矩形面积,其物理意义可理解为:断面过水面积由堤防上、下2部分断面面积组成。西江与北江的平均过水断面面积之比则表示为
(1)
式中:下标xj、bj分别表示西江、北江。
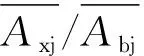
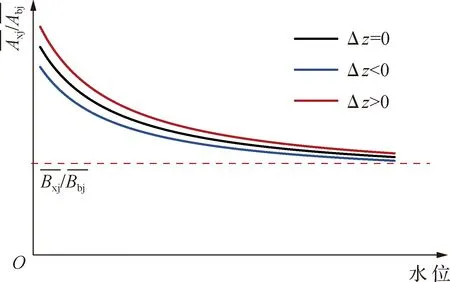
图9 西、北江断面面积比随水位变化Fig.9 Ratio of section area between Xijiang and Beijiang rivers with the water level
(2)
采用思贤滘下游30 km河段的多套地形资料验证两江过水断面面积之比,结果表明,随着水位的升高,西、北江平均过水断面面积之比不断减小,且水位越高减幅越小,比值趋向于稳定(表2及图9)。
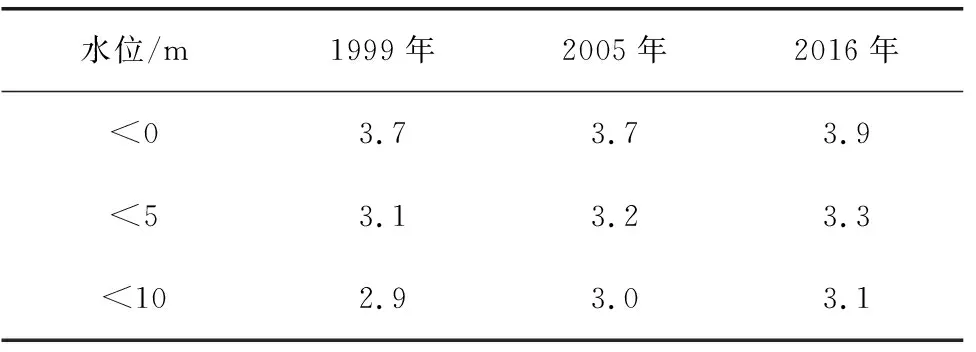
表2 思贤滘下游西、北江河段断面面积比Table 2 Ratio of the crossing section area of the Xijiang and Beijiang rivers at the downstream of Sixianjiao
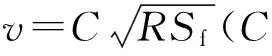

表3 频率洪水水面线下的西、北江地形参数及流量之比Table 3 Topographic parameters of the Xijiang and Beijiang rivers and their flow ratios for water levels corresponding to different flood frequencies
(3)
考虑流速变化后,思贤滘下游15 km内,西、北两江计算流量之比趋近于3∶1,与分流规律一致;思贤滘下游30 km,西、北两江流量之比趋近于3.5∶1,这是由于北江下游15~30 km之间紫洞水文站附近的支汊分流,导致两江流量比值变化。
综上可知,天然条件下,思贤滘下游地形是分流自适应调节的决定性因素,其中,西、北江过水断面面积之比是控制分流比的关键地形参数,水深对分流比有小幅修正作用。
思贤滘下游的西、北江干流至入海口河道总长分别约为145、90 km,且河道沿程多汊道分流,因此有必要进一步研究影响两江分流的关键河段。根据数学模型对下游不同河段河床变化后的分流效果进行计算,见表4,分别对思贤滘下游2.5、7、15、30及60 km河段河床进行改造,结果表明,越往下游,地形变化对分流影响越小,思贤滘下游局部河段(大约7 km左右)是控制两江分流比的节点性河段。

表4 思贤滘下游北江不同河段回填5 m后和西江不同河段下切5 m分流变化Table 4 Changes in flow diversion under different engineering conditions in the river sections downstream of Sixianjiao:a 5 m backfill in different sections of the Beijiang River versus a 5 m incision in the different sections of the Xijiang River
5.2 思贤滘下游变动回水影响
枯水时,思贤滘分流受到下游涨潮动力影响无明显规律,可以归结为下游变动回水的影响。引起变动回水的原因包括:下游水库、湖泊和海洋等水体水位的变化引起的顶托;干流受下游支流涨水的顶托;下游渠道闸门的启闭;下游河道壅水或植被阻力等。受变动回水影响的水流可认为属于稳定渐变流,因为下游水量的变化一般是缓变的,下游回水的顶托引起的比降变化亦是缓变的,因此,受变动回水影响时的流量与各水力因素间的关系可用曼宁公式表示,即
(4)
式中:下标1、2分别表示下游发生变动回水前、后的情况;n为糙率。表明受变动回水影响,下游水体变化引起的水力坡降变化导致河道过流量发生变化,进而影响西、北两江分流比。
基于物理模型,控制西江、北江来流量和来流比不变,通过改变下游边界水位的方法,分别设置3组工况,模拟下游变动回水对思贤滘分流的影响(表5)。为研究西江下游变动回水影响,采用西江为主洪水进行模拟,上游边界为西江100年一遇遭遇北江5年一遇流量,下边界采用插板法壅高水位,见表5。试验表明,西江马口下游水位壅高后,西、北两江流量之比发生变化,但变幅较小,马口水位抬升1 m,三水水位相应抬升0.9 m,两江流量之比由3.1降至2.7。为研究北江下游变动回水影响,采用北江为主洪水进行模拟,上游边界为西江5年一遇遭遇北江100年一遇流量,下边界采用插板法壅高水位,见表5。试验表明,北江三水下游水位壅高后,西、北两江流量之比发生显著变化,三水水位抬升1 m,马口水位相应抬升0.5 m,两江流量之比由3.4升至5.3。综上可知,西、北两江下游变动回水均会导致思贤滘分流的变化,但思贤滘分流对北江下游水位变化更为敏感。由此也可推断,枯季珠江口潮汐上溯动力强,思贤滘下游受潮水顶托影响,不同径潮动力组合作用下的水面比降变化是枯季分流比紊乱的主要原因。

表5 思贤滘下游马口和三水水位变化后的分流情况Table 5 Diversion after the change of Makou and Sanshui water level in the downstream of Sixianjiao
5.3 思贤滘分流计算
ηxj=Qxj/(Qxj+Qbj)
(5)
(6)
选取思贤滘下游两江关键河段的马口、三水断面为计算断面,以水下地形为依据,计算其过水面积、平均水深及水力坡降(表6),根据收集地形资料情况,采用分流比公式(6)分别计算1965年、1974年、1999年、2000年、2005年、2007年及2017年马口年均分流比,在思贤滘附近,马口、三水断面均为沙质河床,式(6)中两汊糙率虽有差别,但与过水面积、水深等相比,其差别要小得多,对分流比应不致有大的影响,因此取思贤滘两汊糙率之比为1。将计算结果与马口水文站实测年均分流比进行对比,见图10。仅考虑地形的影响时,计算值与实际值误差达到6%;同时考虑水力坡降影响时,计算值与实际值误差基本在1%以内(计算地形采用历年马口、三水实测大断面地形,水力坡降根据水文年鉴中的年平均潮位计算)。
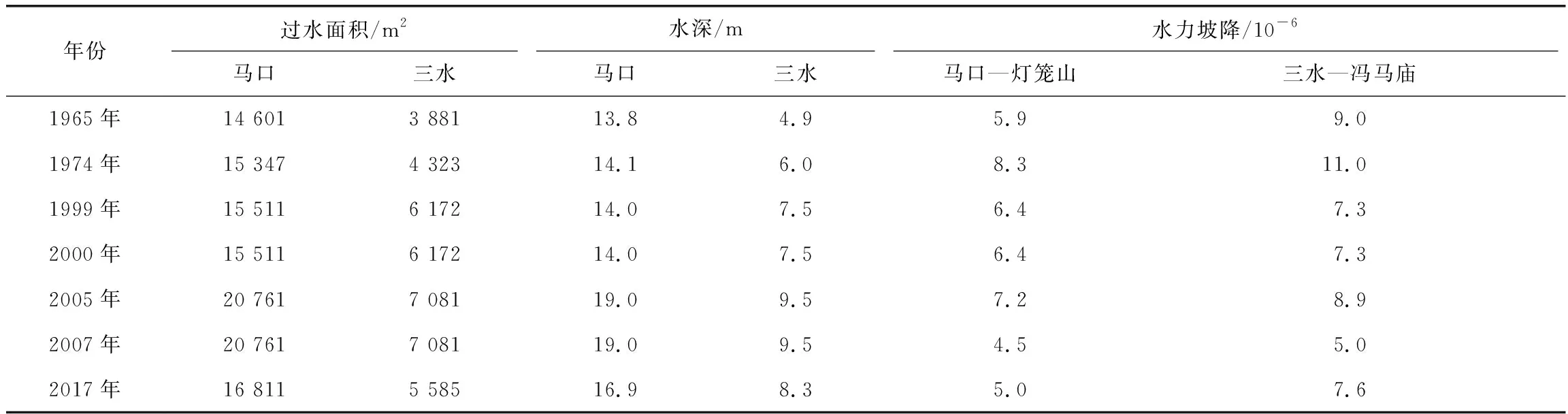
表6 思贤滘分流比计算参数Table 6 Calculation parameters of the Sixianjiao diversion ratio
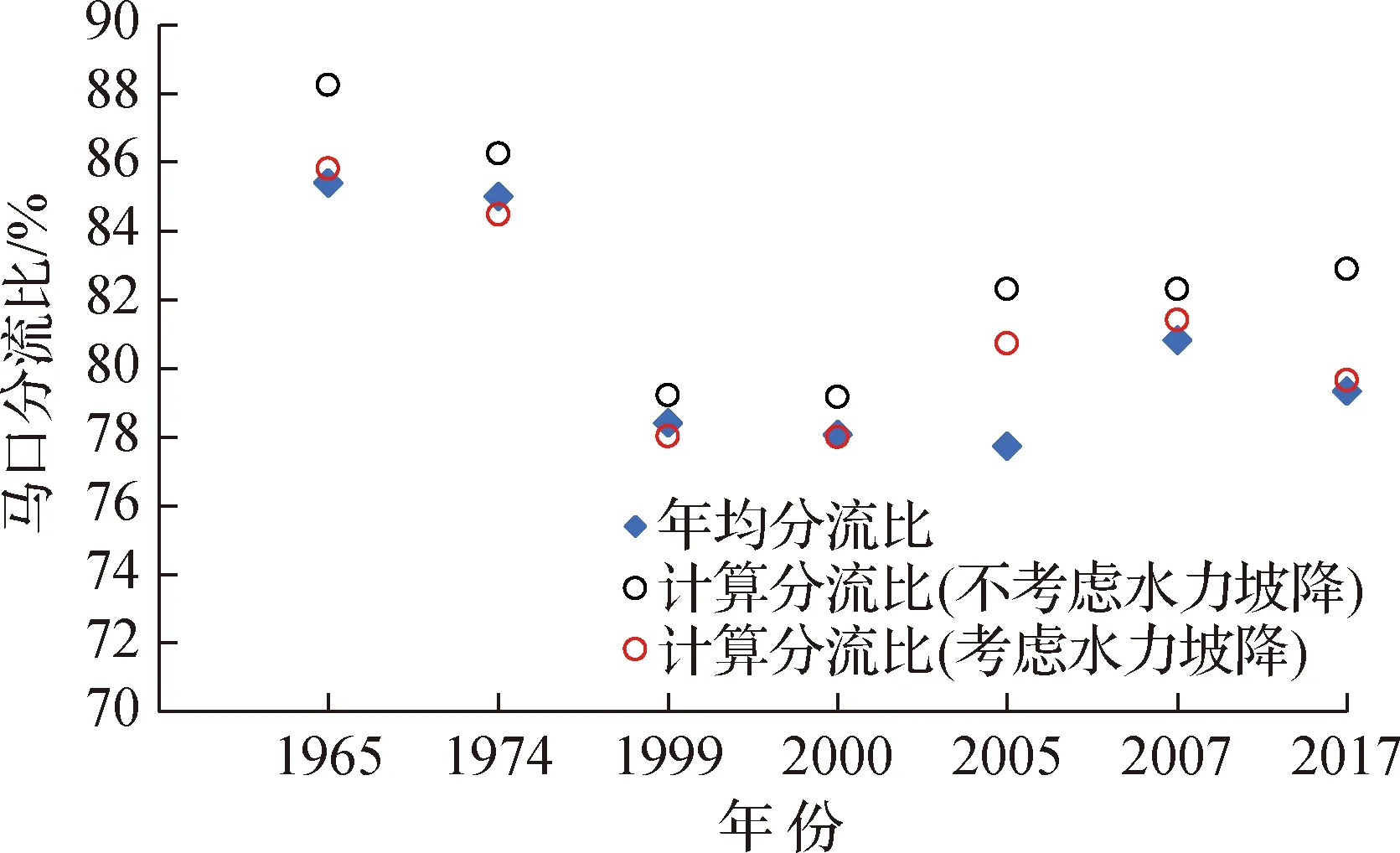
图10 马口分流比实际值与计算值对比Fig.10 Comparison between the actual value and the calculated value of the diversion ratio of Makou
根据分流比计算公式,思贤滘X形汊口分流比受两汊河段的水深、过水面积、糙率及水力坡降控制,而河段水力坡降由上游流量、下游海平面、汊道河床变化共同影响。考虑水力坡降与不考虑水力坡降2种情况下,分流比的计算误差在4%以内,因此可以认为,当上下游水文边界条件不发生明显变化时,两汊河床变化是三水、马口分流比调整的主要原因;当受涨潮动力或建闸等水利工程产生变动回水影响时,水力坡降对分流也产生重要影响。
5.4 讨论
思贤滘分流从年际变化来看,20世纪90年代前,马口分流比枯季为89.4%~93.1%,洪季为83.9%~85.3%;20世纪90年代后,马口分流比枯季为80.7%~85.2%,洪季为76.8%~78.0%。枯季马口分流比始终大于洪季,这是由于汊口分流与过水断面面积有关,流量越小,两江断面面积之比越大,马口分流越多。21世纪以来,洪季马口分流比受地形变化影响有小幅回升趋势,但枯季马口分流比却无明显回升,甚至有下降趋势,枯季汊口涨潮动力较强,潮动力顶托对分流产生变动回水影响,考虑近年来西江干流水道地形不断下切,枯季马口附近涨潮动力增强,由潮动力增强引起马口向三水分流增多,与地形引起的马口分流回升相互制衡,枯季分流比未出现显著回升趋势。综上分析,得到思贤滘“洪季两汊河床控制,枯季潮汐均衡”的分流认识,潮动力的变化使思贤滘汊口洪季与枯季分流比变化趋势出现差异,但究其根本还是由于河网汊道不均匀下切造成的。
6 结 论
本文采用物理模型、数学模型、原型资料分析和理论分析等方法,依据20世纪60年代以来思贤滘区水文地形资料,分析了珠江三角洲顶点思贤滘的分流自适应调节规律,探讨了这种X形汊口的分流机制,主要结论如下:
(1) 思贤滘是一个天然的洪水调节器,具有稳定西、北江洪水分流比的作用。它的分流自适应调整规律表现为:洪水越大,西江马口与北江三水流量之比越稳定,稳定值大致为3∶1左右;枯水期受潮汐影响,规律性不强。
(2) 天然条件下,思贤滘下游地形是分流自适应调整的决定性因素。其中,西、北江过水断面面积之比是控制分流比的关键地形参数,河道河宽受两岸堤防约束,随着流量加大,西、北两江过水断面面积之比趋近于两江河宽之比,致使洪水期两江流量之比趋于定值。思贤滘下游7 km河段是控制两江分流比的节点河段。思贤滘下游水体变化引起水力坡降变化时,思贤滘分流相应改变,这种变化可认为是下游变动回水对分流的影响,思贤滘分流对北江下游水体变化更为敏感。
(3) 未来思贤滘的治理与保护应遵循自然规律,保护河流生态系统,顺应地形演变趋势进行地形微改造,充分挖潜思贤滘的天然调节功能,驱使分流自动适应地形变化,达到调控目标。
——马口窑文献与当代陶艺创作研究展

