金属石墨缠绕垫片蠕变对法兰接头密封性能的影响*
沈伟明 章兰珠 李 科
(1.华东理工大学机械与动力工程学院 上海 200237;2.江苏省特种设备安全监督检验研究院张家港分院 江苏张家港 215600)
螺栓法兰接头具有经济、安全、易于拆装、密封性能优良的特点,广泛应用于石油、化工、航空航天等领域。螺栓法兰接头在工作过程中,很少有因强度不足引起的失效,更多的失效是由于法兰接头的泄漏引起的。特别是当法兰接头在高温环境中工作时,高温不仅会加速垫片的老化和蠕变松弛[1-2],降低其弹性,还会加剧螺栓和法兰的变形。此时,如果出现温度波动,就会引起垫片的热棘轮效应,从而进一步降低垫片上的密封比压,最终导致密封不满足要求而发生泄漏。垫片是法兰连接系统中最关键的密封元件,其力学性能和密封性能直接影响整个法兰接头,而密封垫片的蠕变松弛失效通常是法兰连接失效的主要原因[3-4]。因此,研究密封垫片的密封性能及力学性能,尤其是蠕变松弛性能就显得尤为重要。
目前,学者们已对垫片的蠕变松弛性能进行了深入研究。SAWA等[5-8]详细介绍了密封垫片试验所采用的高温试验装置和试验方法,并研究了温度对垫片蠕变性能的影响以及其对法兰接头密封性能的影响。NECHACHE、BOUZID[9-12]通过理论方法及有限元仿真方法综合分析了兰接头各部分的蠕变、温度,并研究了法兰接头蠕变对密封性能的影响。顾伯勤等[13-14]研制了垫片高温性能试验装置,成功地解决了在高温条件下垫片泄漏率精确测量等技术难题,并提出了高温螺栓法兰连接紧密性的概念。在之前研究的基础上,陆晓峰和沈轶[15]提出了高温法兰接头的可靠性算法和寿命预测方法,考虑了垫片蠕变、螺栓应力松弛和法兰的密封性要求。
虽然垫片的蠕变松弛对法兰接头载荷的影响已得到公认,但在对法兰接头的研究中,目前大多没有考虑垫片的蠕变松弛;另外国内外在研究法兰接头方面大多还是采用数值模拟方法,也有一些学者采用程序来评估螺栓载荷的损失[16],其中垫片的蠕变量是通过理论计算的方式来获得的。章兰珠和毕乐文[17]研究了法兰蠕变速率大于或小于螺栓蠕变速率时对密封性能的影响,其中也忽略了垫片蠕变。本文作者通过对金属石墨缠绕垫片的蠕变松弛试验结果进行拟合,得到金属石墨缠绕垫片蠕变量的表征方法,并结合法兰接头的变形协调方程,通过理论计算获得法兰接头的螺栓残余预紧力;同时建立了法兰接头几何模型,通过有限元分析验证了理论计算结果的准确性。
1 垫片蠕变性能的表征方法
1.1 垫片蠕变松弛试验
蠕变松弛性能表征了材料的尺寸稳定性。一种复合材料,尤其是用于制造精密零件的材料,应具有在即定载荷的持续作用下长期保持其尺寸和形状的能力。由于不同的分子结构或不同的加工和使用条件,各种复合材料的蠕变性能可能会有很大差异,因此有必要对其蠕变松弛能力进行表征。
文中采用浙江某公司生产的DN100金属石墨缠绕垫片进行试验,试验依照EN13555[18]标准进行,加载速率为0.5 MPa/s,升温速率为2 K/s。试验分为两组,第一组保持初始密封比压Sk=110 MPa不变,试验温度分别为100、200、300、400 ℃;第二组保持试验温度400 ℃不变,初始密封比压分别为Sk=70、110、120 MPa。
1.2 垫片蠕变松弛性能的表征
在初始密封比压为110 MPa,测试温度分别为100、200、300、400 ℃时,垫片蠕变松弛试验结果如图1所示。在试验温度为400 ℃,初始密封比压分别为70、110、120 MPa时,垫片蠕变松弛试验结果如图2所示。
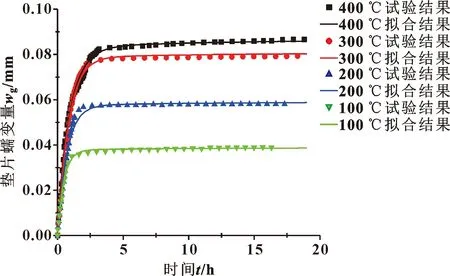
图1 不同温度下垫片蠕变量及拟合曲线(Sk=110 MPa)Fig.1 Gasket creep and fitting curves at different temperatures (Sk=110 MPa)

图2 不同初始密封比压下垫片蠕变量及拟合曲线(T=400 ℃)Fig.2 Gasket creep and fitting curves at different initial sealing pressure(T=400 ℃)
由图1与图2可知,垫片蠕变与工作温度、服役时间以及初始密封比压有关。如图1所示,在初始密封比压相同的情况下,垫片蠕变量会随着工作温度的增加而增加,且在温度较低的区间内(如100~300 ℃),温度升高所造成的垫片蠕变量增幅较大,而在温度较高的区间内(如300~400 ℃),温度升高所造成的垫片蠕变量增幅较小。如图2所示,在试验温度相同的情况下,垫片的蠕变量会随着初始密封比压的增加而增加。
在试验刚开始的较短时间内,垫片会产生一个瞬时蠕变效应,在这段时间内垫片的蠕变速率较快,大部分的垫片蠕变量都在这个时间段内产生,经过1~2 h之后垫片蠕变速率逐渐趋于缓慢。这是由于试验刚开始的阶段是升温阶段,温度的升高导致垫片蠕变量迅速增大,经过升温阶段进入保温阶段时,垫片蠕变速率就会较为平缓。
通过对试验数据进行分析拟合,可以得到垫片的蠕变量随时间的变化规律如式(1)所示。
Δ(t)=Δ(0)+Δ(0)(C1-C2e-C3t+C4lnt)
(1)
式中:t为蠕变时间,h;Δ(t)为垫片在t时间的厚度,mm;Δ(0)为垫片的初始压缩量,mm;C1、C2、C3、C4为拟合参数,C1=2.042×10-2lnT-6.381×10-2,C2=1.975×10-2lnT-6.135×10-2,C3=4.743-6.108×10-1lnT,C4=5.00×10-6+5.15×10-6T,其中T为温度,℃。
2 法兰接头的理论计算
2.1 变形协调分析
法兰接头是一个预应力静不定系统,预紧时各元件发生一定的变形。法兰接头在工作时,介质压力会在法兰接头处产生轴向静压载荷,尤其是在高温情况下更是会加剧法兰、螺栓和垫片的蠕变松弛,此时,法兰轴向位移、螺栓伸长量以及垫片的压缩量与预紧时相比都发生了变化,这些变化量符合法兰接头的变形协调方程,其具体表现形式如式(2)所示[9]。
(2)


式中:hG为螺栓圆中心到垫片作用力的长度,mm;Mf为法兰力矩,N/mm;p为内压,MPa;Kfm为法兰对力矩的刚度,N·mm;Kfp为法兰对内压的刚度,N/mm2;Fb为螺栓力,N;Kb为螺栓刚度,N/mm;Fg为垫片压力,N;Kg为垫片刚度,N/mm;Ap为垫片反力直径所包围的受压区域面积,mm2;hp为从螺栓中心到法兰内径的径向距离,mm。
由以上各式可将式(2)化简为
(3)

2.2 蠕变量的计算
由式(3)可知,计算螺栓预紧力还需要知道各个部分的蠕变量,对于法兰,其蠕变主要造成法兰的偏转角产生变化:
(4)

于是,法兰蠕变造成的轴向位移为
(5)
对于螺栓,由于文中使用的螺栓蠕变本构模型为Norton模型,可表示如下:
(6)

由式(6)可以得到螺栓的蠕变量为
(7)
式中:Ab为螺栓截面积;lb为螺栓有效长度。
对于垫片,则由式(1)得
(8)
2.3 高温对法兰接头的影响
高温工况下,由于法兰螺栓接头不均匀的温度分布和各部件热膨胀系数的不同,常温下达成的变形协调关系会被破坏,螺栓法兰接头因为高温引起的轴向位移由两部分组成,一部分是由法兰、螺栓和垫片3个部件轴向方向热膨胀的相互作用产生的,另一部分是由高温导致法兰偏转引起的轴向位移,即:
wT=αbΔTblb-αgΔTgtg-2αfΔTftf+2hGθfT
(9)
式中:α为热膨胀系数,1/K;ΔT为温差,K;tg为垫片厚度,mm;θfT为由于温度而导致的法兰偏转角,rad,根据文献[20]可查找计算。
3 法兰接头有限元仿真
3.1 法兰接头的尺寸及材料性能
为了验证所得到的垫片蠕变松弛模型,文中选用DN100-PN63的带颈对焊法兰进行分析,接头所使用的螺栓型号为M24,数量为8个,使用金属石墨缠绕式垫片。法兰及垫片的具体尺寸如图3所示。

图3 模型几何尺寸(mm)Fig.3 Dimensions of model(mm):(a)dimension of flange:(b)dimension of gasket
由于法兰接头的结构和所受载荷具有周期对称的特点,故可以沿圆周方向取1/8建立模型,并对模型进行多次分割,以便于划分网格。法兰接头的网格图如图4所示。由于ANSYS软件中的垫片单元不支持蠕变分析,为了模拟垫片的蠕变效应,在法兰模型中加入了一块虚拟刚性板,虚拟板位于垫片中间,厚度为垫片的1/2。加入虚拟板后对法兰接头整体的刚度没有太大影响,在虚拟板蠕变时,由于变形协调,垫片厚度也会产生相应的变化[9,21]。
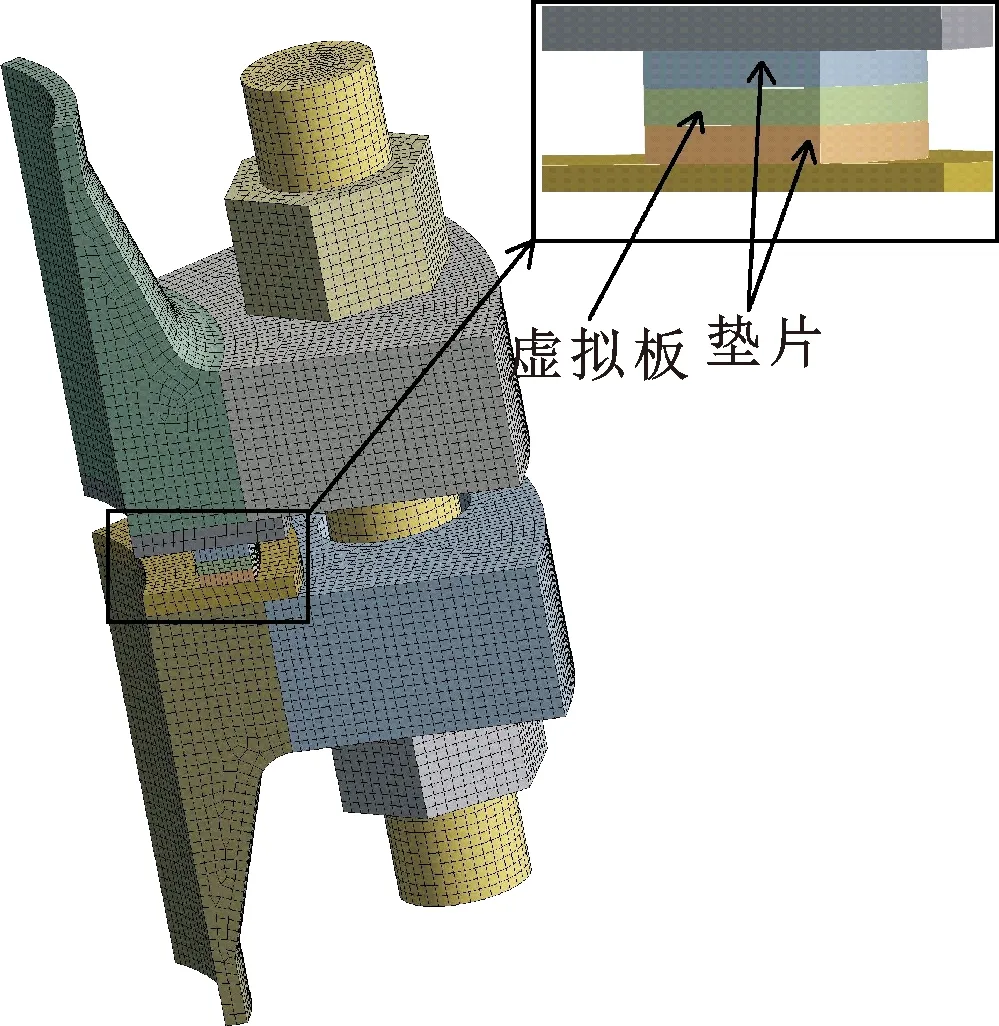
图4 法兰接头有限元计算模型Fig.4 Flange joint finite element calculation model
文中法兰材料使用2.25Cr1Mo,螺栓材料使用A193 B16,其材料性能分别如表1、表2所示。法兰和螺栓材料的蠕变本构关系均采用Norton方程,分别如式(10)和式(11)所示。

表1 法兰材料(2.25Cr1Mo)的物理性能Table 1 Physical properties of flange material (2.25Cr1Mo)

表2 螺栓材料(A193 B16)的物理性能Table 2 Physical properties of bolt materials (A193 B16)
(10)
(11)
3.2 法兰接头温度场分析
在法兰内壁面分别施加100、200、300、400 ℃的均匀温度载荷,并将所有节点的初始温度设置为25 ℃。在模型两侧施加绝热边界条件,将法兰、螺栓与螺母裸露在空气中的表面的对流换热系数设置为3.2×10-5W/(mm2·℃),两法兰之间以及垫片外侧散热较差,故将其对流换热系数设置为1×10-5W/(mm2·℃),法兰接头周围环境设置为25 ℃。
法兰接头温度分布如图5所示。可知,内壁面温度为100、200、300、400 ℃的法兰接头温度变化趋势基本一致,都是内壁面的温度最高,螺栓末端温度最低,并由内壁面往外逐渐降低;且内壁面温度越高,则接头的整体温差就越大,其中内壁面温度为400 ℃时温差最大为127.87 ℃,内壁面温度为100 ℃时温差最小为25.213 ℃。

图5 法兰接头温度场分布Fig.5 Temperature field distribution of flange joint:(a)100 ℃:(b)200 ℃;(c)300 ℃;(d)400 ℃
3.3 法兰接头热固耦合分析


图6 法兰接头载荷及边界条件Fig.6 Loads and boundary conditionsof flange joint
由于螺栓法兰接头主要受预紧、内压、温度、蠕变4个因素的影响,故参考实际法兰工作过程,对法兰接头的加载顺序设置为:(1)施加螺栓预紧力;(2)锁定螺栓力,施加内压载荷;(3)施加温度载荷;(4)打开蠕变设置,进行蠕变计算。
4 解析计算与有限元结果的分析
文中针对考虑垫片法兰螺栓三者蠕变、仅考虑垫片蠕变以及仅考虑法兰螺栓蠕变3种情况,对DN100-PN63的带颈对焊法兰进行100、200、300、400 ℃下的理论计算与有限元仿真,并将蠕变2年的理论计算结果与有限元计算结果进行对比,结果如图7—10所示。
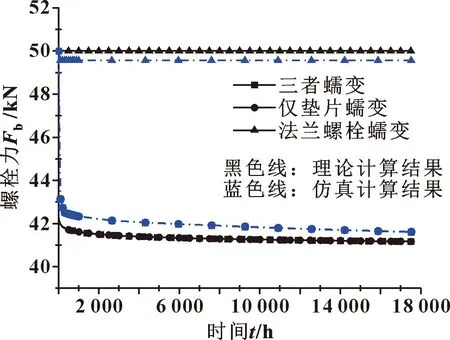
图7 工作温度为100 ℃时螺栓力变化(预紧力50 kN,内压2 MPa)Fig.7 Change of bolt force at working temperature of 100 ℃(pre-tightening force of 50 kN,internal pressure of 2 MPa)

图8 工作温度为200 ℃时螺栓力变化(预紧力50 kN,内压2 MPa)Fig.8 Change of bolt force at working temperature of 200 ℃(pre-tightening force of 50 kN,internal pressure of 2 MPa)
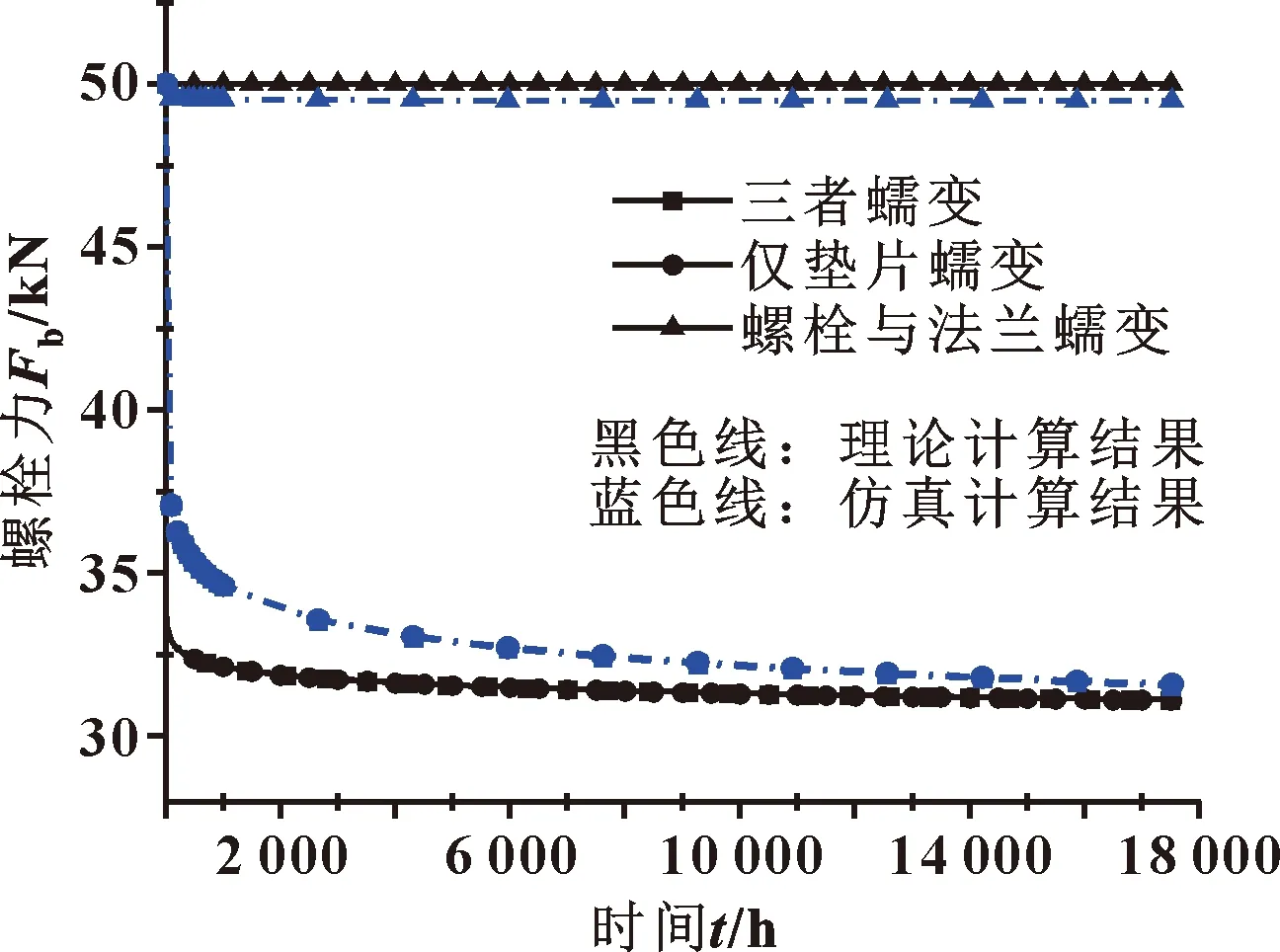
图9 工作温度为300 ℃时螺栓力变化(预紧力50 kN,内压2 MPa)Fig.9 Change of bolt force at working temperature of 300 ℃ (pre-tightening force of 50 kN,internal pressure of 2 MPa)

图10 工作温度为400 ℃时螺栓力变化(预紧力50 kN,内压2 MPa)Fig.10 Change of bolt force at working temperature of 400 ℃(pre-tightening force of 50 kN,internal pressure of 2 MPa)
由图7—10可知,垫片的蠕变松弛所引起的螺栓力减小是较为显著的。工作温度为400 ℃且考虑三者蠕变的情况下,有限元分析结果和由式(3)计算所得的结果都表明,法兰接头在经过了2年的蠕变之后螺栓力的损失超过了40%,且其中大部分的螺栓力减小发生在法兰接头刚工作时的几十个小时之内。从螺栓力减小曲线来看,理论计算结果与有限元结果较为吻合,这表明建立的理论模型较好地反映了实际情况下螺栓法兰垫片蠕变所造成的螺栓力的松弛,使用理论计算式来计算螺栓残余预紧力是较为合理的。
表3中给出了工作温度为100、200、300、400 ℃时,蠕变2年后,考虑三者蠕变、仅考虑垫片蠕变以及仅考虑法兰螺栓蠕变3种情况下理论与有限元计算所得到的螺栓力松弛量百分比。

表3 蠕变引起的螺栓力松弛百分比Table 3 The percentage of bolt force relaxation caused by creep
由表3可知,螺栓力的减小量随着温度增加而增加,这是由于温度的升高导致了垫片、法兰与螺栓蠕变速率的增大,进而导致了螺栓力减小量的增加。且在温度较低的区间内(如100~200 ℃),温度升高所造成的螺栓力的减小量较大,在温度较高的区间内(如300~400 ℃),温度升高所造成的螺栓力的减小量较小,这与前面所提到的垫片蠕变量随温度的变化规律一致。仅考虑垫片蠕变时所产生的螺栓力的减小量与考虑垫片、法兰和螺栓的蠕变时所产生的螺栓力的减小量相差不多,原因是法兰与螺栓所采用的材料都具有较好的抗蠕变性能。在工作温度400 ℃的情况下,仅考虑法兰与螺栓蠕变时,理论计算结果显示螺栓预紧力仅发生了0.39%的减小,有限元计算结果显示螺栓预紧力仅产生了1.04%的减小。在工作温度为100、200、300 ℃的情况下,法兰和螺栓的蠕变速率比400 ℃时更低,理论计算结果显示该3个温度下螺栓力的减小量为0,基本可以忽略不计,有限元计算结果也仅分别为0.87%、0.91%、1.03%。这也说明了在文中模型中垫片蠕变为引起螺栓力下降的主要因素。
仅考虑垫片蠕变时,100、200、300、400 ℃下模型未开始蠕变和开始蠕变2年后的垫片应力云图如图11—14所示。
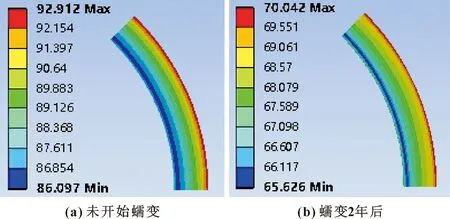
图11 100 ℃时的垫片应力云图(MPa)Fig.11 Gasket stress nephogram at 100 ℃(MPa):(a)creep not started;(b)creep after 2 years

图12 工作温度为200 ℃时垫片应力云图(MPa)Fig.12 Gasket stress nephogram at 200 ℃(MPa):(a)creep not started;(b)creep after 2 years

图13 工作温度为300 ℃时垫片应力云图(MPa)Fig.13 Gasket stress nephogram at 300 ℃(MPa):(a)creep not started;(b)creep after 2 years

图14 工作温度为400 ℃时垫片应力云图(MPa)Fig.14 Gasket stress nephogram at 400 ℃(MPa):(a)creep not started;(b)creep after 2 years
由图11—14可知,垫片蠕变未开始时,在4种工作温度下垫片的受力都很均匀,垫片外侧压力稍大于内侧压力;且在几种工作温度下垫片的最大应力相差不大,如400 ℃时垫片最大应力为92.414 MPa,100 ℃时垫片最大应力为92.912 MPa。在垫片蠕变2年后,工作温度为100、200、300、400 ℃时蠕变后的最大应力与蠕变前的最大应力的比值分别为75.38%、71.55%、62.80%、57.04%,可以看出,垫片的工作温度越高,垫片的最大应力就越小,且工作温度越高,蠕变后垫片的应力分布就越不均匀。
5 结论与展望
对金属石墨缠绕式垫片进行蠕变松弛试验,对试验结果进行拟合,得到其蠕变量的表征方法,将其代入法兰接头变形协调方程中得到螺栓力的减小情况;建立了有限元分析模型,并将理论计算结果与有限元计算结果进行了对比。主要结论如下:
(1)在初始密封比压相同的情况下,温度越大,则垫片的蠕变量越大;在温度相同的情况下,初始密封比压越大则垫片的蠕变量越大,且垫片的蠕变主要发生在试验刚开始的几个小时内。
(2)垫片蠕变对接头蠕变的影响主要发生在前几十个小时,这段时间内螺栓力会产生明显下降。垫片蠕变在接头蠕变中是很重要的一部分,不能忽略垫片的蠕变,某些工况下仅由于垫片的蠕变就可以导致40%以上的螺栓力松弛。
(3)理论计算结果与有限元计算结果较为吻合,表明建立的理论计算模型可用于评估法兰接头螺栓力损失。
然而文中虽证明了垫片蠕变在接头蠕变中是不可忽略的一部分,但在研究过程中存在着以下不足:
(1)在实际情况下,不只法兰、螺栓、垫片的蠕变会对螺栓力产生影响,温度的波动、接头内流体的压力变化等也会对其造成影响,在理论计算和有限元仿真中忽略掉了这些因素的影响。
(2)在法兰接头的理论计算中,忽略了法兰轮毂的蠕变效应,并认为接头各部分只在螺栓轴向方向上存在蠕变,这导致理论计算结果与实际情况相比偏小。

