偏心摆式飞剪机剪切过程的机械参数优化设计

牟宏昌

四川九洲电器集团有限公司,重庆 621000

0 引言

随着各行业机械化水平的不断提升,优化机械参数成为提升机械化水平的重点,偏心摆式飞剪机一般用于板材生产,尤其是连续的板材生产过程中,连续式板材生产中需要固定尺寸,保证剪切过程的完整性和均匀性,避免出现拉钢或者堆钢现象。通过对偏心摆式飞剪机运动轨迹进行优化,确保优化后的飞剪机整体结构与轧件剪切过程完全匹配,这是满足轧件剪切需求的关键条件。

1 偏心摆式飞剪机工作原理

在轧钢生产过程中,飞剪机是常见的设备,飞剪机能够将运动中的轧件横向剪短,对提升轧件的工艺水平有着重要价值。从剪刃接触钢坯开始,直到钢坯被剪断为止,这个过程的运动轨迹要合理高效,才能满足轧件剪切的要求,提升轧件的剪切质量[1]。本文选择的偏心摆式飞剪机有2个自由度,结构为七杆结构,刀架杆、剪刃的运动轨迹与普通七杆结构一致,剪刃分为K和A,钢坯在进入剪切区域后,在剪刃的相对运动下,运行中的轧件被横向剪断,剪刃K和剪刃A在运动中既有相对移动下的剪切动作,也有水平方向的运动轨迹[2]。

在剪切过程中,需要遵循3个要点:剪刃K和剪刃A的运动轨迹要有重合度,才能将轧件剪断;剪切过程需要减少剪刃K和剪刃A的阻力,避免剪刃K和剪刃A相互干扰,因此需要剪刃K和剪刃A垂直于轧件后进行剪切,这个过程中,刀架杆与轧件呈现垂直关系;剪切过程中,剪刃K和剪刃A水平方向的速度要均匀,与轧件的运行速度保持一致。偏心摆式飞剪机剪切过程的参数要满足这3个要点,因此需要针对参数进行优化设计,运用模型得到实际符合要求的参数值。

2 优化方法

2.1 优化设计

选择基本杆组子函数法和ADAMSView中的DOT2优化工具,从剪刃重合度、剪刃与钢板位置角以及剪刃水平速度3个要点中设立目标函数,使参数设计能够与工艺要求保持一致,最终达到机械参数优化设计的生产目标,提升偏心摆式飞剪机的剪切性能和质量。

2.2 运用基本杆组子函数法的优化方法

2.2.1 选择变量

本次建模中所选的变量有飞剪机剪切结构中的杆长,剪切结构固定架的坐标,曲柄的初始角度,具体参数如表1所示,设计变量x1～x11为杆长的变化,结构参数中,L01D～LFX为曲柄的角度变化,X0、Y0、θ为固定架的坐标变化。

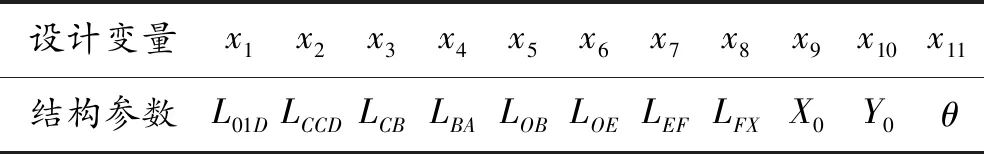
表1 设计变量与结构参数

2.2.2 设立目标函数

根据飞剪机的剪切要点,剪切结构的优化目标有3点:通过优化使剪切轨迹的重合度与钢坯的剪切尺寸相符合;通过优化使剪切过程中剪刃与钢坯保持90°的位置角;通过优化使剪刃在剪切过程中保持均匀的水平方向速度。基于此,优化的目标函数包括重合度和剪切尺寸要求的轨迹误差、剪切杆的位置角误差、速度均匀误差,目标函数使用线性加权方法进行构建。

2.2.3 设立约束函数

在约束条件中设置边界条件和性能条件,变量中的杆长要大于0,飞剪机结构中的曲柄在转动过程中没有任何外界因素干涉,设立相应的约束函数,针对主动件的整周转动设立性能约束条件,完成各个极限位置的整周转动目标。

2.2.4 选择优化方法

在优化过程中,考虑到初始点和迭代点均在可行区域内,选择内点惩罚函数作为优化方法,子函数为目标函数和约束函数,调用子函数时选择Powell函数,完成优化计算,目标函数中的运动变量使用运动学模型进行计算[3]。通过建立摆式飞剪机运动学模型函数,将剪切机拆分为2个单杆构件,由主动杆、连杆、滑块等组成不同杆组,使用各杆组的运动学模型建立剪切机的运动模型,将主动件的参数输入到模型中,能够得出剪切机结构在整周转动中的关键点以及杆件轨迹参数,在这个基础上计算除目标函数的变量,即剪刃的位置坐标参数、剪刃杆件位置角参数以及剪刃水平移动速度参数。

2.2.5 分析优化结果

通过对剪切过程的参数优化,偏心摆式飞剪机剪切过程的整体性能得到了提升,此次优化所选的优化变量中主要是重合度、位置角和水平运动速度,若需要对飞剪机的初始尺寸进行优化,需要优化初始位置的最大闭合度,此方案能使得轨迹重合度与原始尺寸的轨迹重合度保持一致。与优化前的剪刃轨迹参数相比,优化后的剪刃重合度明显有了提升,最大开口度更大,设备的剪切能力有了很大提升。在优化前,偏心摆式飞剪机的剪刃平均速度变化幅度大,平均速度一般为0.32～0.38 m/s,与工艺要求的0.4 m/s有着较大差异,通过优化,剪刃的水平运动速度达到了0.4～0.45 m/s,满足了轧件剪切工艺的要求,速度比优化前更加均匀。优化后,刀架杆位置角度非常接近90°,与优化前的82°相比,满足了剪刃与轧件垂直的要求。

2.3 运用DOT2工具的优化方法

2.3.1 目标函数的设计

根据3个要点的设计目标,运用虚拟技术进行参数优化,首先需要建立相应的目标函数,目标函数要体现虚拟技术的运用目标,即优化剪切机结构运动轨迹,因此目标函数为剪切过程中剪刃与轧件的垂直度以及剪切过程中剪刃水平运动均匀度。分目标函数为刀架杆的摆动角度与垂直方向的最小误差、剪刃水平速度与轧件运行速度的最小误差,采用直接加权法构建统一目标函数,分目标函数的变动范围要设立约束条件,使用模型函数计算分目标函数的容限和加权因子。

2.3.2 变量的设计

运用虚拟技术进行参数优化,需要设计相应的变量,此次选择的变量为飞剪机构杆长、固定支座坐标、曲柄初始角位置。

2.3.3 约束条件的设计

曲柄整周转动时,需要有相应的约束条件,此次所选的五杆机有2个曲柄,为了使曲柄达到整周转动的目的,需要将5杆转化为4杆,其中一个曲柄的主杆长度要比其他3杆长度要小,在5杆机构转化为4杆机构的过程中,曲柄的约束条件主要是传动角约束。

2.3.4 建立模型

使用ADAMS软件能够建立参数实体模型,同时,结合多体系统动力学原理,建立偏心摆式飞剪机运动方程,对运动轨迹进行计算。ADAMS具有自动建立方程和求解的功能,能够完成建模目标,用户无需进行编程,只需要在操作界面输入相关参数,例如结构参数、连接参数、力学参数等,这方便了用户的编程过程,使得用户可以轻松进行目标参数的优化。

首先需要输入飞剪机的各初始位置,此次选用的参数与设备的一般参数一致,使用飞剪机剪切10 mm厚度的钢板,钢板在飞剪机中的运行速度为1 950 mm/s,飞剪机在将钢板完全切断的情况下,2个剪刃的重合度要大于5 mm。基于这个目标,使用ADAMSView软件建立飞剪机剪切过程的结合模型,在集合模型中添加飞剪机剪切过程的运动轨迹,对曲柄运动进行定义,运用ADAMSView提供的测量并监测曲柄摆角、剪刃垂直距离2个指标,通过测量,取得飞剪机剪切过程中2个剪刃的垂直距离变化幅度为5～10 mm,曲柄的摆角幅度为-1.925～-2.140 rad。之后,对模型起始位置进行调整,将剪切过程的位置作为起始位置,增加sensor传感器监测摆角范围,将曲柄的摆角范围设置在-1.925 ～-2.140 rad,最后将剪切过程限制在仿真计算范围之内,完成剪切过程参数优化设计的几何模型制作。此次优化设计的变量为各杆长度、曲柄的初始角度、支座的位置坐标,将各杆关联的位置坐标作为变量参数。使用ADAMSView提供的测量可以获取测量点的相关数组,被测目标的测量点所记录的测量值组成数组后,使用ADAMSView中内置的数学函数、矩阵函数、数组函数计算测量的一维数组,可以建立起目标函数和约束函数。之后使用ADAMS中的优化工具DOT2做相应的优化计算,DOT2中内置了序列线性规划法,即SLP法,能够对约束函数进行优化,SLP序列线性规划法作为工程领域常用的工程设计方法,其应用原理为将非线性约束问题优化为线性约束问题,然后利用线性规划方法求出相应的参数,参数与目标函数并非完全一致,但与目标函数近似,因此需要设立1个收敛误差限,通常为10×10-3。若目标函数相近的2次值差产生的绝对值不大于收敛误差限值10×10-3,本次优化便达到了目标。

2.3.5 优化结果分析

优化前后的几何参数对比如表2所示。在优化前后,剪切过程的目标函数有了明显的变化,剪刃轨迹、水平速度与刀架杆位置角均发生了相应的变化,目标函数在经过多次迭代后呈现收敛趋势,这说明优化结果与最优值是相近的,符合优化预期。通过使用DOT2进行参数优化,偏心摆式飞剪机剪切过程中,2个剪刃的最大重合度符合15 mm的剪切要求,最大开口度符合剪切每秒移动1 950 mm钢板所需的75 mm开口度,满足了钢板剪切的整体需求,并提升了飞剪机的剪切性能,经过优化后,飞剪机剪切最大速度上升到1 961.115 mm/s,最小速度增长到1 918.768 mm/s,刀架杆的剪切摆角幅度保持在1.627 2～1.604 8 rad,较优化前的1.627 2～1.606 3 rad有了明显改善。

表2 设计变量优化前后尺寸对比

3 结束语

本文通过运用2种优化方法,对飞剪机的剪切过程进行了优化设计。第1种方法运用了基本杆组子函数法,对设立的目标函数和约束函数进行优化,实现了3个要点的优化目标,使得重合度、位置角、水平速度与工艺要求保持了一致,使飞剪机的剪切性能得到了优化,因此可以作为有效的优化方法进行推广。第2种方法运用了ADAMSView中的DOT2优化工具,通过建立飞剪运动学仿真模型,对剪切过程中剪刃与轧件的垂直度和剪刃的水平运动速度进行优化,缩短了参数优化设计的时间,提高了参数优化的效果。相比基本杆组子函数法,DOT2优化工具的效率更高,优化目标函数的接近值较为准确,因此建议在参数优化设计中使用DOT2优化工具,提高设备运行的整体水平。